Как найти углы треугольника вписанного в квадрат - Сайт, где вы сможете решить свои вопросы

«Треугольник, вписанный в квадрат с их одной общей вершиной, угол при которой равен 45°» — данная конструкция обязательно должна разбираться при подготовке к профильному ОГЭ или ЕГЭ.

В этой конструкции так много любопытных и потрясающих фактов, что считаю знакомство с «треугольником в квадрате» непременным шагом при совершенствовании своих навыков в планиметрии.

Задача 24 ОГЭ (услож. 262 вар. Ларина)

На сторонах BC и CD квадрата ABCD взяты точки E и F, причём ∠EAF = 45°. Отрезки AE и AF пересекают диагональ BD в точках P и Q. Докажите, что площадь △AEF в два раза большие площади △APQ.

https://alexlarin.net/gia/trvar262_1_oge.html

Указания к решению (дополнено 16.11.2020)

См. ранее опубликованные статьи статьи:

1. Удивительный треугольник в квадрате

2. Удивительный треугольник в квадрате

Поворот квадрата

Источник

Firstly We can write
(1) Oklid relation from $triangle CNB$

$h^2=m(k+x)$

(2) Pisagor relation from $triangle DPN$

$a^2=(x+k)^2+(x+k+m-h)^2$

(3) Pisagor relation from $triangle FRN$

$b^2=h^2+k^2$

(4) Pisagor relation from $triangle DCF$

$c^2=x^2+(x+k+m)^2$

if DNF triange is a right triangle,It must satisfy $a^2+b^2=c^2$.

$(x+k)^2+(x+k+m-h)^2+h^2+k^2=x^2+(x+k+m)^2$

$(x+k)^2+(x+k+m)^2-2h(x+k+m)+h^2+h^2+k^2=x^2+(x+k+m)^2$

$(x+k)^2-2h(x+k+m)+2h^2+k^2=x^2$

$xk+k^2-h(x+k+m)+h^2=0$

$xk+k^2-h(x+k+m)+m(k+x)=0$

$-h(x+k+m)+(k+m)(k+x)=0$

$frac{x+k}{x+k+m}=frac{h}{k+m}$

This result is equal to the rates of thales formula for similar triangles $triangle CRN sim triangle CBE$

Thus $a^2+b^2=c^2$ is correct for $triangle DNF$ .

Источник

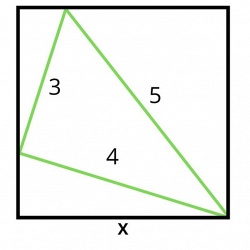
Проверьте свою логику с этой интересной геометрической задачей: Найдите длину стороны квадрата

Тесты

Вам предлагается решить логическую задачу, используя приёмы элементарной геометрии, и, возможно, некоторые алгебраические трюки.

Задача на логику

Внутри квадрата вписан треугольник со сторонами 3, 4 и 5.

Найдите длину стороны этого квадрата (Х).

Одно из решений данной задачи появиться чуть позже.

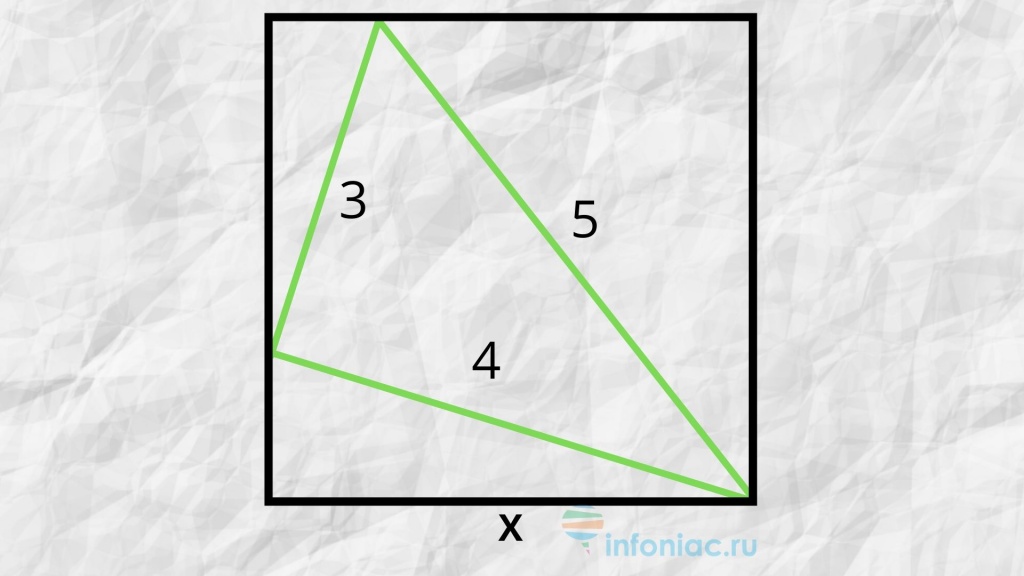
Решили? Делитесь своим решением и ответом в комментариях.

Заметьте, что треугольник имеет стороны 3, 4 и 5, а это значит, что перед вами египетский треугольник. Особенность такого треугольника в том, что все три стороны его целочисленны, то есть длины всех его сторон выражаются целыми числами. Согласно теореме, обратной теореме Пифагора, такой треугольник прямоуголен. Угол между сторонами 3 и 4 равен 90 градусов.

Теперь давайте обратим внимание на другие два треугольника. Они подобны, но это нужно доказать. Это можно сделать доказав, что у них все три угла одинаковые.

Один угол имеет «а» градусов, значит другой угол будет равен 90-а градусов.

Теперь давайте посчитаем угол в другом треугольнике. Отметим, что этот угол имеет «b» градусов. d = 180 — 90 — (90-а) => b = а. А раз и в одном, и в другом треугольники два угла равны, то и оставшиеся также равны

Как это нам поможет?

Давайте сначала обозначим один катет вот этого треугольника «y», а другой катет «x«.

Так как один их катетов равен стороне квадрата, вот это расстояние будет равно x-y.

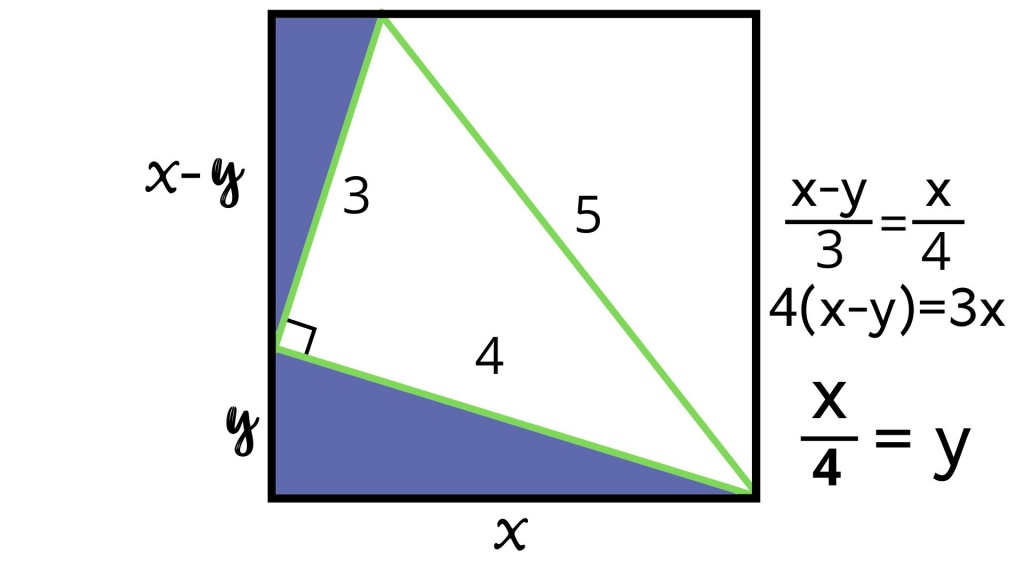
Теперь используем тот факт, что эти треугольники подобны. Соотношение длинного катета и гипотенузы у них равны. То есть (x-y)/3 = x/4. Узнаем, чему равен y (используем метод перекрестного умножения): 4(x-y)=3x => y=x/4.

Заменим это значение в этом треугольнике.

Мы в соцсетях

Tik-Tok

Теперь мы можем узнать, чему равен x, так как у нас прямоугольный треугольник. По теореме Пифагора получаем: x 2 +(x/4) 2 =16, то есть 17/16x 2 =16 и для x>0 мы имеем x=16/√17 и это наш ответ.

Сколько углов у треугольника

Сколько углов у треугольника? Ответ на этот вопрос заложен в самом названии фигуры.

Тре угольник — фигура, имеющая три угла. У треугольника любого вида есть ровно три угла.

Например, углы треугольника ABC —

угол A, угол B и угол C.

Для обозначения угла используют специальный знак: ∠.

Запись ∠A читают как «угол A».

Угол можно назвать также тремя буквами.

При этом название вершины угла обязательно должно стоять посередине:

Сколько тупых углов у треугольника?

В треугольнике может быть только один тупой или один прямой угол.

Например, в тупоугольном треугольнике MNP

один тупой угол — угол M

и два острых — угол N и угол P.

Сколько прямых углов у треугольника?

В прямоугольном треугольнике KFT

Треугольник вписанный в окружность

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — не диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:

Площадь треугольника

Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

Периметр треугольника вписанного в окружность,
если известны все стороны:

Сторона треугольника

Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:

Средняя линия треугольника

l — средняя линия треугольника.

Средняя линия треугольника вписанного
в окружность, если известно основание:

Высота треугольника

Высота треугольника вписанного в окружность,
если известна площадь и основание:

[ h = b cdot sin alpha ]

Свойства

Центр вписанной в треугольник окружности
находится на пересечении биссектрис.
В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну.
Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора.
Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров.
Все вершины треугольника, вписанного
в окружность, лежат на окружности.
Сумма всех углов треугольника — 180 градусов.
Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

Проведем серединные
перпендикуляры — HO, FO, EO.
O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника.
Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Источник

Квадрат. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):

Можно дать и другие определение квадрата.

Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.

Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).

Свойства квадрата

Длины всех сторон квадрата равны.
Все углы квадрата прямые.
Диагонали квадрата равны.
Диагонали пересекаются под прямым углом.
Диагонали квадрата являются биссектрисами углов.
Диагонали квадрата точкой пересечения делятся пополам.

Изложеннные свойства изображены на рисунках ниже:

Диагональ квадрата

Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

(1)

Из равенства (1) найдем d:

(2)

Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.

Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:

Ответ:

Окружность, вписанная в квадрат

Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):

Формула вычисления радиуса вписанной окружности через сторону квадрата

Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:

(3)

Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.

Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:

Ответ:

Формула вычисления сторон квадрата через радиус вписанной окружности

Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:

(4)

Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.

Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:

Ответ:

Окружность, описанная около квадрата

Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):

Формула радиуса окружности описанной вокруг квадрата

Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.

Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:

(5)

Из формулы (5) найдем R:

(6)

или, умножая числитель и знаменатель на , получим:

(7)

Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.

Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:

Ответ:

Формула стороны квадрата через радиус описанной около квадрата окружности

Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.

Из формулы (1) выразим a через R:

(8)

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:

Ответ:

Периметр квадрата

Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

(9)

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:

Ответ:

Признаки квадрата

Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.

Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).

Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть

(10)

Так как AD и BC перпендикулярны, то

Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда

(12)

Эти реугольники также равнобедренные. Тогда

Из (13) следует, что

(14)

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).

Шеллир: XIV – TEMPERANCE (УМЕРЕННОСТЬ)

На карте изображен золотоволосый Ангел с бесстрастным лицом, в белых одеждах, с огненно-красными крыльями, одной ногой стоящий в воде, а другой – на земле. В традиционных колодах Ангел андрогинен, обозначая гармоничное слияние мужского и женского. На лбу Ангела – солярный символ, золотой диск с точкой посередине, на груди – знак семерицы, треугольник в квадрате. В руках он держит две золотые чаши (в некоторых колодах – золотую и серебряную или синюю и красную), переливая из одной в другую некую жидкость. Справа от Ангела растут желтые ирисы, слева – начинается дорога, уводящая к горизонту и проходящая между двух гор. Фон карты – серый, в небе – восходящее солнце в форме короны, находящееся уже несколько выше, чем на предыдущем Аркане, Смерти.

Рассмотрим символы этого Аркана:

Солнечный знак на лбу Ангела указывает на его роль проводника к поднимающемуся на горизонте солнцу.

Семерица: Треугольник, вписанный в квадрат – распространенный символ. Квадрат тут обозначает материю, треугольник – стремящийся ввысь дух; тройка и четверка дают в сумме семерицу, знак божественности.

Красные крылья Ангела – знак духовной подвижности и активности.

Чаши. Серебряная (синяя) чаша в левой руке – символ подсознания, золотая (алая) чаша в правой руке – символ сознания, что указывает нам на то, что в подсознании заключен источник, вечно питающий сознательную сторону человеческой личности. Кроме того, чаша вообще является символом вместилища божественного духа.

Жидкость течет непрерывным потоком, но не переполняет чашу, что указывает на постоянную сбалансированную связанность сознательного и бессознательного.

Желтые ирисы. Сами по себе ирисы являются символом света и надежды. Желтый цвет (цвет золотой середины) показывает, что эту надежду даст только гармоничное единство подсознательное и сознательного. Кроме того, ирисы – частый символ вестника богов или же психопомпа, проводника душ. Надо сказать, что в некоторых колодах вместо ирисов изображаются асфодели, что напоминает нам о том, что, несмотря на светлые и чистые краски этой карты, сюжет ее относится все же к происходящему на ночной, подземной части пути по Арканам.

Тропа, уходящая к горизонту, означает, что цель еще не достигнута.

Две горы, между которыми проходит дорога, напоминают нам о грядущих опасностях на пути (прохождение между Сциллой и Харибдой), а также о необходимости равновесия и умении не впасть в крайности – пройти по лезвию бритвы между добром и злом.

Фигура, которую мы видим на этой карте не оставляет ощущения статичности – создается впечатление, что краснокрылый Ангел движется навстречу, очень плавно и неторопливо: легкое движение воздуха от крыльев, всплеск воды, шорох одежды… Это неудивительно: вестник, который встречает нас на полях асфоделей – Психопомп, «душеводитель», сопровождающий в дальнейшем пути души, вышедшие из вод Смерти 13-го Аркана. Психопомп – один из эпитетов Гермеса, который, кроме прочих своих функций, отводил души умерших в подземный мир. Этот бог – хранитель границ и порогов, покровитель троп и дорог, и в силу этого он может свободно бродить по обе стороны от разделяющей черты, связывая мир живых и мир мертвых, небо и землю.

Нельзя забывать, что в алхимической традиции Гермес – символ гармоничного соединения противоположностей: материи и духа, металла и жидкости, холода и пламени, яда и лекарства. Черты этой двуединости во множестве представлены в рисунке Аркана. Алхимический символ Гермеса – ртуть, которая, по убеждениям алхимиков, вступает в реакцию только с благородными металлами. Аллегорически это означает, что Гермес указывает ищущему путь к внутреннему духовному сокровищу.

В юнгианской психологии тоже есть термин «психопомп», обозначающий проводника между ясным и логичным миром сознательного и иррациональным миром подсознательного – эту функцию принимает на себя Анима/Анимус, персонификация женского образа в психике мужчины и, соответственно, мужского в психике женщины. Как и Гермес алхимиков, внутренняя женщина и внутренний мужчина указывают человеку путь к его конечному предназначению, к его судьбе, основной жизненной цели, к внутреннему сокровищу. Если обратиться к мифологическим сюжетам, то мы увидим, как вела Персея Афина, Тесея – Ариадна, как сопровождала Энея в мире мёртвых кумская сивилла. Анимус в аналогичных женских мифах представлен преимущественно не как проводник и помощник, но как ускользающий образ: Психею ведет исчезнувший Амур, Герду – украденный Кай, Гретель уводит Гензеля от злой ведьмы и т.п.

В сказках душеводитель часто приобретает образ какого-нибудь предмета: если вспомнить русские сказки, то Баба Яга, например, отправляя героя в царство Кощеево (подземный, навий мир), тоже дает ему «проводника»: либо волшебного водяного коня (в самых архаичных сказках – кстати, тут надо обращать внимание, что герой этого коня получает не за красивые глаза, а заработав своим горбом), либо какой либо предмет: клубочек, золотое яблоко, которые катятся перед героем и указывают ему путь. В нескольких сказках я встречала образ полотенца, которое Баба Яга стелет на землю у своего порога, и оно превращается в тропу, по которой и уходит герой.

Нумерологически в дневном ряду карта связана с Арканом Первосвященника: и там и там мы видим четко выраженную функцию посредничества: священник связывает людей с богом, психопомп – мир живых с миром мертвых, но и функция проводника присутствует в обеих картах: Ангел 14-го Аркана ведет души по полям асфоделей, Иерофант своими наставлениями указывает путь в мире живых.

Значение именно умеренности, верной меры, золотой середины определяется самим положением Аркана – между 13-м Арканом, Смертью, полным отказом от чего-либо, и 15-м, Дьяволом, обозначающим в первую очередь излишества. Умеренность стоит между ними, указывая на необходимость не впадать в крайности.

Эта карта – знак верного пути, на который вы только что вступили. Это время коротенькой передышки (до самых гор дорога ровная и пустынная), когда можно успокоить дыхание, оглядеться вокруг и привести свое сознание в состояние чистоты и уравновешенности – это одно из обязательных условий прохождения 14-го Аркана, тем более, что душевный покой и гармония необходимы душе, идущей по полям асфоделей: путь долог, полон неожиданностей и препятствий. На этом этапе нет шансов сбиться с пути – дорога впереди ясно видна, да и идет человек не один, а с проводником, – поэтому, кстати, эта карта часто указывает на некую личность, которая станет (или уже стала) для кверента временным помощником, «указующим перстом», советчиком. Вряд ли контакт с такой личностью-помощником станет долгим, но свою функцию она выполнит, подтолкнув человека в нужном направлении.

Карта Умеренности, как и все другие Арканы теневого ряда, фактически никогда не выступают сигнификаторами, хотя их использование возможно – к примеру, по астрологическому принципу.

В раскладах она довольно многозначна, но в прямом положении и без негативных окружающих карт значение ее благоприятно. В раскладах на тип личности она укажет на человека уравновешенного, но не лишенного живости и авантюрной жилки, хорошо владеющего как умением читать между строк, так и получением невербальной информации. В советах – на необходимость придерживаться меры во всем происходящем. Если человек поглощен работой или каким-либо делом – неплохо напомнить ему о необходимости отдыха, и наоборот.

В раскладах на здоровье значение Аркана зависит от сопутствующих карт, но может указывать на проблемы с тазобедренными и коленными суставами, на необходимость йогических или других подобных практик. Перевернутая может указать на любые проблемы, связанные с неумеренностью – от ожирения до переутомления.

Коротко по значениям:

В прямом положении :

Верная мера, умение не переборщить, сбалансированность, уравновешенность, умеренность.

Посредничество. Хорошее чувствование других людей. Действие с учетом индивидуальных особенностей окружающих.

Выход к началу верного пути.

Помощник, советчик, проводник.

Способность к анализу и синтезу.

В перевернутом положении :

Неумеренность, слепая односторонность.

Неверный подход к жизни и окружающим. Чрезмерна эмоциональность или холодность. Перепады настроения.

Треугольник вписанный в окружность

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны: