Тема: Как рассчитать углы в усечённой пирамиде? (раскрой фанеры) (Прочитано 18910 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Как рассчитать углы в усечённой пирамиде? И раскроить фанерные заготовки?
Исходные данные — высота и размеры оснований (симметричто, например, снизу 60х80см, сверку 20х50см высота 40см)
Нужно знать углы (для раскроя на плоскости) и углы “заваливания” кромок (в т.ч. сверху и снизу и, соответственно, припуск на них)
Через школьную стереометрию sin/cos как-то совсем заумно получается (или существуют готовые формулы?).
Может есть какие-то технологические способы для решения таких задач?
Просьбы высказываться только имевшим дело.
За ответы по-существу заранее спасибо!
« Последнее редактирование: Августа 31, 2012, 02:36:48 pm от 11 »
Записан
Именно углы? Имхо, через длины сторон гораздо проще получается – нужно найти расстояние между противоположными вершинами в параллелепипеде (60-20)/2 х (80-50)/2 х 40 = 20х15х40
Потом начертить чертёж в автокаде и померить угол
« Последнее редактирование: Августа 31, 2012, 02:40:08 pm от Murzzzilk »
Записан
Огромное спасибо!
Угол задаётся между основанием и гранью или между основанием и ребром?
“Blade Tilt” – это наклон диска при пилении по наклонной стороне или по основанию?
Это относится к правильной пирамиде? А как поступить в моём случае, если основания – неподобные друг другу прямоугольники?
Если ещё существуют какие-то способы/on-line калькуляторы, то буду благодарен за ссылки (желательно с картинками и без привлечения автокада и т.п. — как-то же сотни лет рассчитывали это поточно, значит должен существовать какой-то арифметический способ (или рассчитывались только плоские заготовки, а скосы каким-то образом запиливались “по месту”?))
« Последнее редактирование: Августа 31, 2012, 03:03:51 pm от 11 »
Записан
Pluton
Огромное спасибо!
Угол задаётся между основанием и гранью или между основанием и ребром?
“Blade Tilt” – это наклон диска при пилении по наклонной стороне или по основанию?
Это относится к правильной пирамиде? А как поступить в моём случае, если основания – неподобные друг другу прямоугольники?Если ещё существуют какие-то способы/on-line калькуляторы, то буду благодарен за ссылки (желательно с картинками и без привлечения автокада и т.п. — как-то же сотни лет рассчитывали это поточно, значит должен существовать какой-то арифметический способ (или рассчитывались только плоские заготовки, а скосы каким-то образом запиливались “по месту”?))
На этой неделе кто-то выкладывал в Екселе, только вот найти не могу в какой теме
Записан
Пользователи, которые поблагодарили этот пост: forester
На этой неделе кто-то выкладывал в Екселе, только вот найти не могу в какой теме
Вместо цитаты СПАСИБО нажал, если что звиняйте
тема называлась Я помогу, мне помогут
http://forum.woodtools.ru/index.php?topic=44686.msg812297#msg812297 кажись эта
и там вроде были расчеты как резать плинтус на торцовке
скачал там немного не то, хотя с какой стороны подойти
« Последнее редактирование: Августа 31, 2012, 03:24:34 pm от forester »
Записан
Pluton
кажись эта
Нет, не эта. В той было несколько калькуляторов и таблица
Записан
Не оно?
Экселевская табличка, в которой есть: расчет дуг, сегментов, лестниц, витых лестниц, упругость материала, двойные углы, многоугольники, арки, эллипсы, пропорции и пр.
Подозреваю, что искомая Вами информация была в ветке МАСТЕРИМ САМИ/ КАК ОТРЕЗАТЬ ПОД 45 ГРАДУСОВ, посмотрите.
« Последнее редактирование: Августа 31, 2012, 05:08:57 pm от росс »
Записан
Пользователи, которые поблагодарили этот пост: 11
вячеслав и.
Записан
Пользователи, которые поблагодарили этот пост: 11
Ну вот вроде для случая правильной пирамиды углы считаются, а как для моего случая (неподобные прямоугольники)?
« Последнее редактирование: Августа 31, 2012, 06:44:22 pm от 11 »
Записан
“Blade Tilt” – это наклон диска
tilt – это именно наклон диска,а miter angle – это градусы поворота базы.
Записан
« Последнее редактирование: Сентября 01, 2012, 06:36:34 pm от ter »
Записан
Пользователи, которые поблагодарили этот пост: 11
VirusE
Про линтус я выкладывал http://forum.woodtools.ru/index.php?topic=44686.0 выложил файл для расчета (в принципе для торцовки, но принцип один). Считал для плинтуса, но метод подойти должен. Задаешь два угла (угол наклона стенок от вертикали и углы стыковки стенок на виде сверху) и получаешь угол поворота стола и угол наклона пилы.
Угол наклона стенок – расчитать можно как арктангенс отношения половины разницы оснований пирамиды к ее высоте. Под этим же углом и кромки заваливать естественно (в эксель забиваешь “=ATAN((А-Б)/(2*С))*180/пи()” где А – ячейка с длиной нижнего основания, Б – длина верхнего основания, С высота пирамиды. умножать на 180 и делить на Пи нужно для того что бы в градусы перевести.
Подходит не только для квадратных коробок (угол 90 градусов), но и для многоугольных (например для шестиугольных – угол 120 градусов), можно и ромб засандалить (например углы 60 и 120).
Записан
Записан
Делайте то, что любите делать и в вашей жизни не будет ни одного рабочего дня. (Конфуций)
- Мастеровой »
- Наши работы »
- Мастерим сами (Модератор: Андрей Вл) »
- Как рассчитать углы в усечённой пирамиде? (раскрой фанеры)
Зная стороны оснований усеченной пирамиды, можно вычислить внутренний угол оснований, представленных правильными многоугольниками, периметры и площади оснований усеченной пирамиды, а также радиусы вписанной и описанной около оснований окружностей, воспользовавшись формулами для правильных многоугольников.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
Боковое ребро усеченной пирамиды дает возможность рассчитать через трапеции во внутреннем и боковом пространстве пирамиды апофему и высоту, а также углы между ними и основаниями.
Чтобы найти апофему усеченной пирамиды, рассмотрим боковую грань, представляющую собой равнобедренную трапецию, разделенную апофемой на две конгруэнтные прямоугольные трапециями, основаниями которых являются половины сторон оснований самой пирамиды. Исходя из этого апофема равна по теореме Пифагора квадратному корню из разности квадрата бокового ребра и квадрата разности половин сторон оснований пирамиды. (рис. 50.2)
f=√(d^2-(b/2-a/2)^2 )=√(d^2-(b-a)^2/4)
Чтобы найти высоту усеченной пирамиды, рассмотрим трапецию во внутреннем пространстве тела, между высотой и боковым ребром. Основаниями такой трапеции служат половины радиусов описанных окружностей вокруг оснований усеченной пирамиды. Следовательно, формула высоты по аналогии с апофемой выглядит следующим образом. (рис. 50.3)
h=√(d^2-(R_b-R_a )^2 )
Чтобы рассчитать углы при основаниях усеченной пирамиды и боковом ребре, можно воспользоваться в этой же трапеции/прямоугольном треугольнике тригонометрическими отношениями и принципом суммы углов трапеции.
cosδ=(R_b-R_a)/d
ε=180°-δ
Углы при основаниях и апофеме усеченной пирамиды можно вычислить в трапеции, которую апофема образует с высотой пирамиды подобным образом, через радиусы вписанных в основания окружностей. (рис. 50.4)
cosβ=(r_b-r_a)/f
α=180°-β
Площадь боковой поверхности усеченной пирамиды состоит из n-ного количества равнобоких трапеций, площадь каждой из которых равна произведению полусуммы оснований трапеции на ее высоту, то есть, перекладывая на измерения пирамиды – полусуммы сторон оснований пирамиды на ее апофему. Чтобы найти площадь полной поверхности, нужно прибавить к полученному значению обе площади оснований усеченной пирамиды.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны оснований и боковое ребро, можно найти через высоту и площади оснований, найденные по указанным выше формулам.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
Усечённая пирами́да — многогранник, часть пирамиды, заключенная между основанием и плоскостью, параллельной основанию.
Связанные определения[править | править код]
- Основание изначальной пирамиды, а также параллельная ему грань называются основаниями усечённой пирамиды.
- Остальные грани называются боковыми.
Правильная усечённая пирамида
- Если изначальная пирамида правильная то её усечённая пирамида также называется правильной.
- Высота боковой грани называется апофемой.
Свойства[править | править код]
- Боковые грани усечённой пирамиды представляют собой трапеции.
Правильная усечённая пирамида[править | править код]
Главная
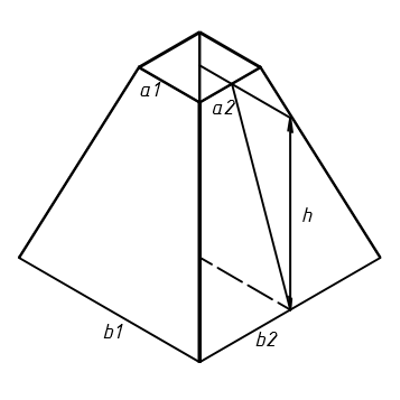
Расчёт параметров усеченной четырёхгранной пирамиды
Параметры усечённой четырёхгранной пирамиды:
Можно использовать для расчета параметров прямой четырёхугольной призмы – для этого строна a1 = b1 и, соответственно a2 = b2 .
В качестве разделителей разряда использовать не запятую, а точку.
a1 – длина первой стороны меньшего основания, мм:
a2 – длина второй стороны меньшего основания, мм:
b1 – длина первой стороны большего основания, мм:
b2 – длина второй стороны большего основания, мм:
h – высота пирамиды, мм:
s – толщина развёртки, мм:
ρ – плотность материала, кг/м3:
Объём усеченной пирамиды, мм 3: , м 3: ,
л.
19.09.2022