Чему равны углы равностороннего треугольника?
Теорема
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.

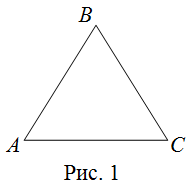
AB=BC=AC
Доказать: ∠A=∠B=∠C=60º.
Доказательство:
Так как AB=BC, ∠A=∠C (как углы при основании равнобедренного треугольника).
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать.
Замечание.
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
Углы равностороннего треугольника
Чему равны углы равностороннего треугольника?
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать .
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
[spoiler title=”источники:”]
http://matworld.ru/geometry/reshenie-treugolnikov.php
[/spoiler]
Содержание:
- Определение равностороннего треугольника
- Свойства равностороннего треугольника
- Примеры решения задач
Определение равностороннего треугольника
Определение
Равносторонним треугольником называется такой треугольник
$ABC$, у которого все стороны равны:
$AB = BC = AC$.
Свойства равностороннего треугольника
- В равностороннем треугольнике все углы равны.
-
Любая биссектриса, равностороннего треугольника равна его медиане и высоте.
Если сторона равностороннего треугольника равна
$a$, то$$l_{a}=m_{a}=h_{a}=frac{a sqrt{3}}{2}$$
Примеры решения задач
Пример
Задание. Определить, чему равны углы в равностороннем треугольнике.
Решение. По свойству равностороннего треугольника, в нем все углы равны. Обозначим эту величину через
$x$, то есть
$alpha=beta=gamma=x$. Так как
сумма всех углов треугольника равна
$180^{circ}$, справедливо равенство
$$alpha+beta+gamma=180^{circ}$$
Подставим $x$:
$$
begin{array}{c}
x+x+x=180^{circ} \
3 x=180^{circ} \
x=60^{circ}
end{array}
$$
Ответ. В равностороннем треугольнике все углы по
$60^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Дан равносторонний треугольник со стороной
$a=2 sqrt{3}$. Найти высоту, опущенную на одну из сторон.
Решение. Для нахождения высоты воспользуемся формулой
$$h_{a}=frac{a sqrt{3}}{2} Rightarrow h_{a}=frac{2 sqrt{3} cdot sqrt{3}}{2} Rightarrow h_{a}=3$$
Ответ. $h_{a}=3$
Читать дальше: что такое разносторонний треугольник.
Правильный (равносторонний, или равноугольный) треугольник — это правильный многоугольник с тремя сторонами, простейший из правильных многоугольников. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.
Содержание
- 1 Свойства
- 2 Правильный сферический треугольник
- 3 Теоремы о равностороннем треугольнике или содержащие его
- 4 См. также
- 5 Примечания
Свойства[править | править код]
Правильный тетраэдр состоит из четырёх правильных треугольников.
Пусть a — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
- Радиус вписанной окружности правильного треугольника, выраженный через его сторону:
- Радиус описанной окружности правильного треугольника, выраженный через его сторону:
- Периметр правильного треугольника:
- Высоты, медианы и биссектрисы правильного треугольника:
- Площадь правильного треугольника рассчитывается по формулам:
- Радиус описанной окружности равен двойному радиусу вписанной окружности:
- Правильными треугольниками можно замостить плоскость.
- В правильном треугольнике окружность девяти точек совпадает с вписанной окружностью.
Правильный сферический треугольник[править | править код]
Для любого значения в интервале от 60 до 180 градусов существует правильный сферический треугольник с равными этому значению углами.
Теоремы о равностороннем треугольнике или содержащие его[править | править код]
- Задача Наполеона
- Прямая Симсона одно из свойств
- Теорема Вивиани
- Теорема Морли
- Теорема Наполеона
- Теорема Помпею
- Теоремы Тебо 2 и 3
- Точки Аполлония
- Точки Торричелли
См. также[править | править код]
- Замечательные прямые треугольника
- Замечательные точки треугольника
- Равнобедренный треугольник
- Теорема Чевы
- Треугольник
- Треугольник Рёло
Примечания[править | править код]
Символ Шлефли |
|
|---|---|
| Многоугольники |
|
| Звёздчатые многоугольники |
|
| Паркеты на плоскости |
|
| Правильные многогранники и сферические паркеты |
|
| Многогранники Кеплера — Пуансо |
|
| Соты |
{4,3,4} |
| Четырёхмерные многогранники |
|
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})
Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. (R=2cdot r)
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка( O) – центр треугольника.
Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).
Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Поэтому (OB=2cdot OK), то есть (R=2cdot r).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.