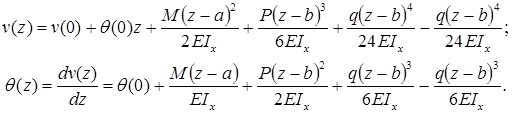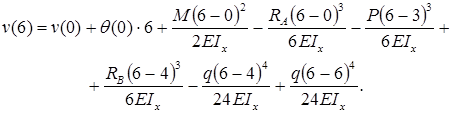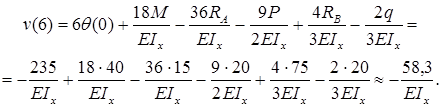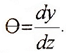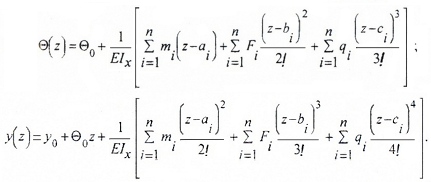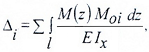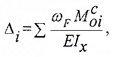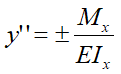Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
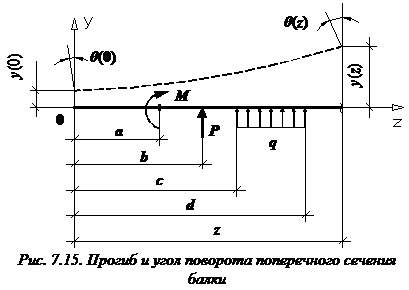
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 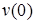
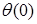
Уравнение упругой линии балки на примере
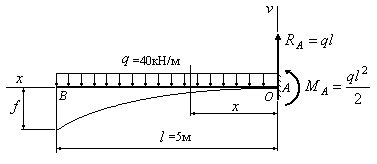
Определим прогиб балки на консоли при 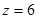
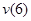
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 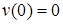
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
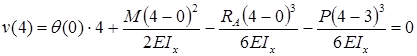
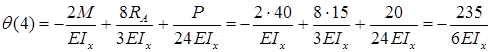
Прогиб консоли при z=6м:
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
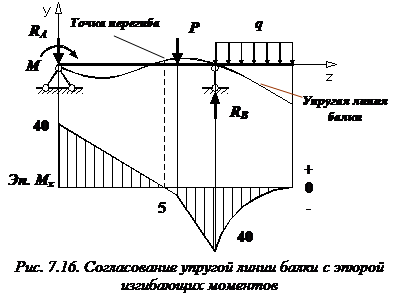
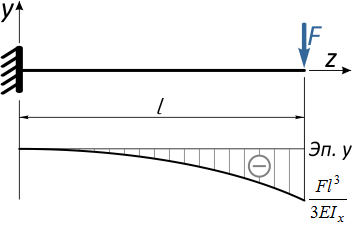
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
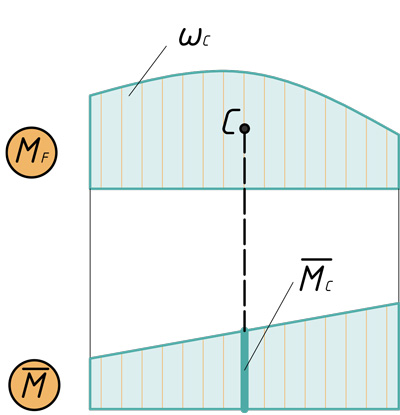
({ V={ M }_{ F } }cdot overline { M } ={ omega }_{ C }cdot { overline { M } }_{ C } )
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
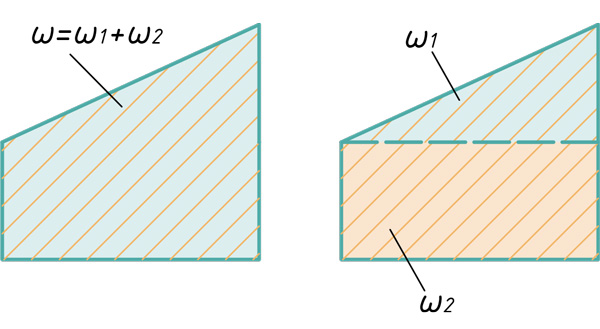
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
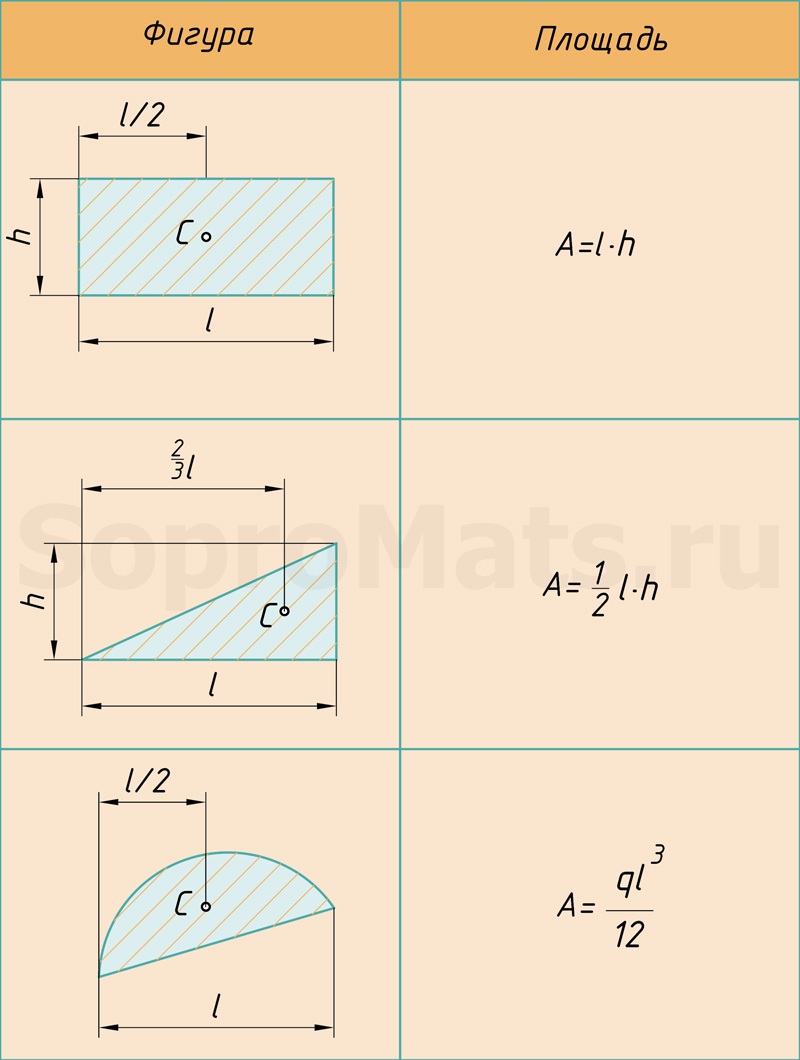
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
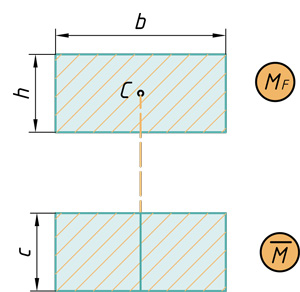
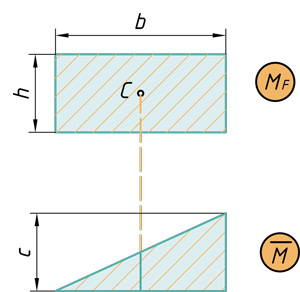
Прямоугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot c } )
Прямоугольник на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ bcdot hcdot frac { 1 }{ 2 } cdot c } )
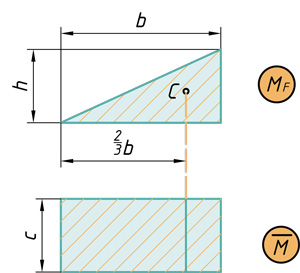
Треугольник на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { 1 }{ 2 } cdot bcdot hcdot c } )
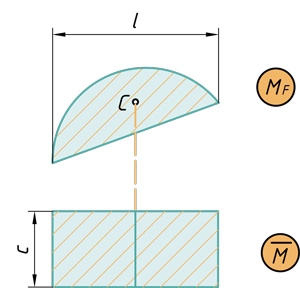
Параболический сегмент на прямоугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot c } )
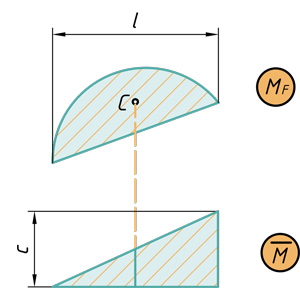
Параболический сегмент на треугольник
( { V={ M }_{ F } }cdot overline { M } ={ frac { qcdot { l }^{ 3 } }{ 12 } cdot frac { 1 }{ 2 } cdot c } )
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
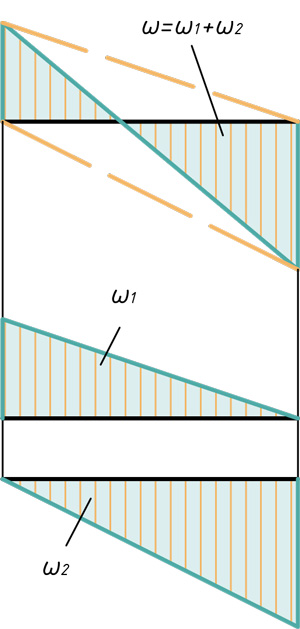
Прямоугольник и треугольник
Два треугольника
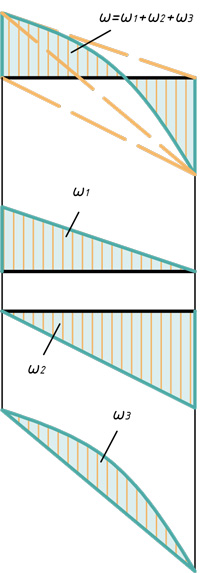
Два треугольника и параболический сегмент
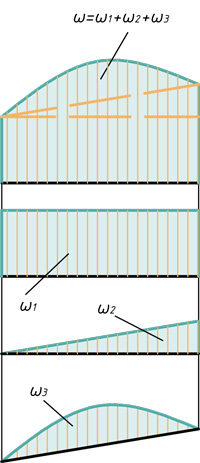
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
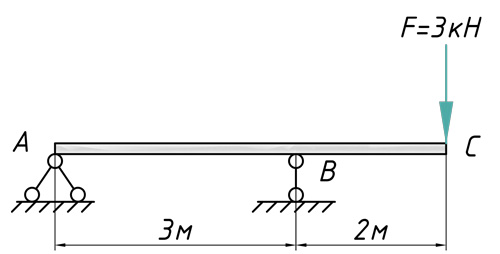
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
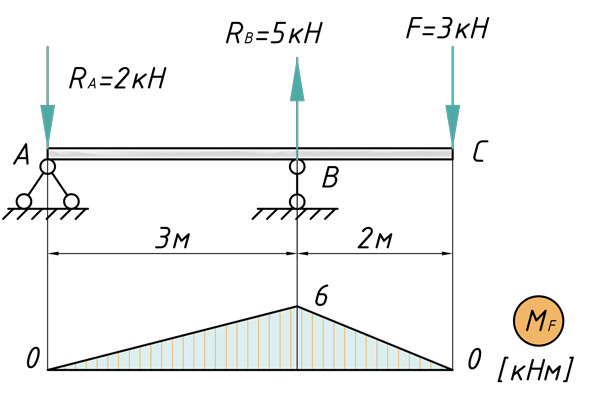
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
[ { V }_{ C }=frac { 1 }{ E{ I }_{ x } } (frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 2 }{ 3 } cdot 2+frac { 1 }{ 2 } cdot 6cdot 2cdot frac { 2 }{ 3 } cdot 2)=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } ]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
[ { V }_{ C }=frac { 20кН{ м }^{ 3 } }{ E{ I }_{ x } } =frac { 20cdot { 10 }^{ 9 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =0.289см ]
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
[ { theta }_{ C }=frac { 1 }{ E{ I }_{ x } } (-frac { 1 }{ 2 } cdot 6cdot 3cdot frac { 1 }{ 3 } cdot 1)=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } ]
[ { { theta } }_{ C }=-frac { 3кН{ м }^{ 2 } }{ E{ I }_{ x } } =-frac { 3cdot { 10 }^{ 7 }Нcdot { см }^{ 3 } }{ 2cdot { 10 }^{ 7 }frac { Н }{ { см }^{ 2 } } cdot 3460{ см }^{ 4 } } =-0.0004рад ]
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
В прошлой части мы обсудили, как может изменяться момент стержня и как выяснить, не разрушится ли он под действием нормальных и касательных сил. Однако под воздействием момента стержни могут изгибаться и изменять форму, что может приводить к неправильной работе конструкций или даже их разрушению в процессе эксплуатации. Сегодняшняя статья посвящена вопросу нахождения прогибов и углов наклона при изгибе.
Уравнение кривой
В прошлой части мы выяснили, что для нахождения момента нам необходимо знать какой у дуги изгиба радиус кривизны, какой у сечения статический момент и какой модуль Юнга у материала балки:
Затем мы устранили из уравнения такое значение как радиус кривизны, из наших уравнений, так как нас не столько волновало, как под воздействием изменится балка, сколько не сломается ли она.
Однако сейчас нас интересует именно то, как будет деталь изгибаться под воздействием моментов, как будет меняться геометрия .
В прошлый раз мы не заостряли внимание на вопросе «что такое радиус кривизны», да и просто «что такое кривизна». В этой части мы данную проблему решим, а также объясним как это значение поможет нам в сопромате вычислить деформации изгиба.
Фактически, до этого момента мы оперировали не столько радиусом, сколько кривизной, которая обратно пропорциональна радиусу:
А сейчас мы поговорим о том, какое значение она имеет с точки зрения геометрии.
Если нет желания смотреть, как с точки зрения математики выводятся геометрические характеристики, можно промотать до следующего жирного шрифта и принять за данность выводы.
Кривизна – это то, насколько сильно изменяется угол наклона касательной к нашей кривой за единицу длины дуги.

Так как любую кривую можно представить как сумму бесконечно малых дуг, принадлежащих разным окружностям, стоит посмотреть, на сколько будет изменяться угол в двух точках ее дуги.

Углы будем измерять в радианах (180°=π, 360°=2π). Длина окружности равна удвоенному произведению радиуса на π: l=2πR. Круг — фигура симметричная, и поэтому в любой точке кривизна будет одинакова и равна:
χ=frac{2π}{2π*R}=frac{1}{R}
Вот так и находилась формула кривизны балки. И теперь мы хотим поставить её на службу поиска формы балки.
Нам нужно найти изменение угла за бесконечно малый пройденный путь, и мы имеем некоторую функцию. При этом её первая производная будет равна тангенсу угла с осью x, которую мы обозначим греческой тета θ:

Нам же для вычисления кривизны необходимо найти изменение угла θ:
Гуглим таблицу дифференциалов, находим, что дифференциал от тангенса равен следующему выражению:
d(arctg (x))=frac{dx}{1+x^2}
Так как функция сложная (y’ — тоже какая-то функция, пусть нам и не известная), получившееся значение надо будет домножить на производную от аргумента:
dθ=frac{dx}{(1+(y’)²)}*y’’
Кривизна же — это изменение угла за пренебрежительно малый отрезок длины:
Уравнение угла наклона нам известно. Теперь нам нужно вычислить длину малой дуги. Достаточно малой, чтобы можно было пренебречь кривизной и считать её прямой. Тогда мы сможем воспользоваться теоремой Пифагора:
Где dx – пройденный путь по оси x, а dy – по оси y.
Нам для красоты уравнения хотелось бы избавиться побыстрее от дифференциалов, чтобы в формуле остались только производные. Для этого мы делим все, что было под корнем на (dx)^2:
frac{(dx)^2}{(dx)^2}+frac{(dy)^2}{(dx)^2}=1+(y')^2
Так как (dx)^2/(dx)^2=1, а (dy)/(dx) – это производная y по x.
Чтобы уравновесить данное вмешательство, мы должны домножить все выражение на dx (т.к. √(dx)^2=dx):
Теперь у нас есть все для нахождения кривизны:
χ=frac{dθ}{dl}=frac{dx}{(1+(y’)^2)}*y’’*frac{1}{dxsqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^2}
*frac{1}{sqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^{{3}}}
Отсюда стоит читать всем, даже тем, кому математика вывода кривизны не очень интересна.
Итак, мы смогли вычислить чему равна функция кривизны:
χ=frac{1}{R}=frac{y’’}{(sqrt{1+(y’)^2})^{3}}
Где y – прогиб (т.е. расстояние на которое выше или ниже окажется определенная точка балки, по сравнению с недоформированным состоянием), y’ – первая производная от неё, а y» – вторая (или кривизна).
Перед нами же стоит задача вычислить форму. Так как в сопротивлении материалов прогибы достаточно небольшие, изменением длины можно пренебречь. Следовательно, нам остается лишь вычислить изменение координаты y в зависимости от x. И в полученной формуле нам мешает это сделать очень объемный знаменатель (√(1+(y’)²)³.
Если подумать логически, то так как прогибы в сопромате достаточно небольшие, можно было бы не учитывать производную y’, так как она является отношением катетов треугольника, который бы получился опусти мы к оси x перпендикуляр.
Дело в том, что даже если прогиб (координата y) будет составлять 1/10 от x, производная в самом крайнем углу будет чуть больше 0,2x. А ее квадрат 0,04x. А (√(1+(y’)²)³ около 1,06.
Это не назвать пренебрежительно малым значением, однако его проще компенсировать коэффициентами запаса прочности. Да и прогиб этот слишком большой для основ сопротивления материалов (большими деформациями занимается отдельная дисциплина). Вот демонстрация прогиба в натуральном соотношении:
В результате, если мы проигнорируем знаменатель, получим формулу, которую уже можно будет использовать в дальнейших расчетах:
χ=θ’=y’’
Угол поворота и прогиб
Мы уже выяснили, что кривизна балки в каждой части зависит от момента, возникающего в этом сечении, статического момента и модуля Юнга материала, из которого это балка сделана:
Сегодня же мы будем решать обратную задачу и находить изгиб балки. В первой части статьи мы выяснили, что для малых изгибов радиус кривизны (он равен единице деленной на радиус кривизны) практически равен второй производной от прогиба (насколько по оси z поднимется или опустится балка в конкретной точке). В итоге мы, зная как распределяется момент, сможем посчитать вторую производную прогиба для каждой точки балки:
y’’=χ=frac{1}{R}=frac{M_z}{I_z×E}
Нам же интересна форма балки: углы её наклона и на сколько сантиметров выше или ниже она окажется.
Начнём с наклона. Как мы уже выяснили, первая производная будет равна тангенсу наклона. Тангенс равен отношению противолежащего катета к прилежащему:

Углы наклона у нас будут маленькими, поэтому прилежащий катет будет практически равен радиусу. Отношение противолежащей стороны к радиусу является синусом:

А синус малого угла, как мы уже выяснили вначале статьи, численно равен углу в радианах.
Примечание: мы выяснили, что для малых углов тангенс, синус и угол численно равны. Эта закономерность важна не только в сопромате, но и в большинстве других инженерных наук. Например, в геодезии, при определении величины малых скатов.

Как следствие, для того, чтобы найти угол наклона, нам необходимо проинтегрировать кривизну:
θ=∫y''dx=∫frac{M_z*dx}{J_z*E}=frac{1}{J_z*E}∫M_z*dx=y'+C
Углы и прогибы балки под воздействием момента
В простейшем случае к балке приложен только момент:

В таком случае значение момента является константой. Обозначим ее как M. Тогда найти прогиб можно по формуле:
θ=∫y''dx=frac{1}{I_z*E}∫M_z*dx=frac{M_z*x}{I_z*E}+C
Остается найти константу интегрирования. Так как в начале координат балка жестко закреплена, угол в месте закрепления будет равен нулю, как следствие, константа тоже будет равна нулю. Эпюра угла наклона будет выглядеть вот так:

Для того, чтобы найти прогибы надо, соответственно, проинтегрировать получившееся выражение еще раз:
y=∫θdx=∫frac{M_z*x*dx}{I_z*E}+∫Cdx=frac{M_z*x^2*dx}{2*I_z*E}+Cx+D
Константу C мы уже знаем, а константу D можно найти по той же логике: балка жестко закреплена в начальной точке, а значит прогиб y в ней будет равен 0. А полученная нами формула приводит к нулю в начале координат только при нулевой константе:
(M*0)2/2+C*0+D=0, только если D=0
Ну а эпюра прогибов будет выглядеть следующим образом:

Углы и прогибы балки под воздействием силы
В случае же, если момент появляется под воздействием силы, эпюры как бы сдвигаются на одну вперед:

Линейной станет функция момента, а угол будет постепенно увеличиваться (вначале быстро, потом медленнее, так как момент будет меньше).
Mz=P(l-x), где Mz— момент возникающий в балке в точке, которая расположена на расстоянии x от места закрепления балки, а l – длина балки.
Получили мы это уравнение следующим образом: мы знаем что в месте закрепления возникает момент который компенсирует момент от воздействия силы на конце балки:
Также в месте закрепления будет возникать сила, которая будет компенсировать силу внешнюю:
Когда мы будет отдаляться от точки закрепления на величину x, сила реакции опоры будет создавать для нашего сечения момент MRa=Ra*x. Он будет складываться с моментом передавшимся с начала балки:
M_z=M_{z_{0}}-M_{R_{a}}=\=p*l+R_a*x=P*l-P*x=\=P(l-x)
Зная функцию распределения момента мы можем найти функции наклона и прогиба.
Наклон будет увеличиваться по параболе:
θ=∫frac{(P*(l-x))*dx}{I_z*E}=frac{P*(l-x)^2}{2*I_z*E}+C

Ну а прогиб будет изменяться уже по кубическому закону:
y=∫frac{P*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{P*(l-x)^3*dx}{6*I_z*E}+C*x+D
Примечание: если проще, то l-x потому, что в нулевой координате момент равен расстоянию до силы, а затем уменьшается на то расстояние, которое мы до нее прошли

Углы и прогибы балки под воздействием равномерно-распределенной нагрузки
В случае с равномерно-распределенной нагрузкой ситуация абсолютно аналогична: эпюры «сдвигаются» на одну относительно воздействия силы. Поперечная сила изменяется по линейному закону Qy=Ra-qx=ql-qx=q(l-x), момент по параболе Mz=q(l-x)2/2:

Угол наклона, соответственно, будет определяться кубической функцией:
θ=∫frac{q*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{q*(l-x)^3*dx}{6*I_z*E}+C

А прогиб уже функцией четвёртой степени:
y=∫frac{q*(l-x)^3*dx}{6*I_z*E}=\=frac{q*(l-x)^4*dx}{24*I_z*E}+Cx+D

Расчет балки на прогибы и углы наклона. Метод начальных параметров. Пример
На практике достаточно редко случается ситуация, при которой на конструкцию действует только одна сила, а сама конструкция состоит из одной балки, закрепленной только в одном месте. Разберем как пример расчёт балки, в которой есть все виды воздействий:

Примечание: среди внешних воздействий отсутствует сила. Мы сделали это для того, чтобы не загружать статью лишними расчётами: сила реакции опоры в расчетах ничем не отличается от силы внешней.
Первым делом, нужно заменить места закрепления на силы, которые они создают для поддержания равновесия балки. В данном случае это две вертикальные силы (моментов шарнирные опоры не создают):
Теперь наша задача найти эти силы. Сделать это довольно просто: составляем уравнение сил по оси y и момента для точки закрепления балки.
Уравнение равновесия сил по оси Y:
R_a-ql+R_b=R_a-30+R_b=0, R_a+R_b=30
Уравнение равновесия момента в левой точке закрепления:
M_a=ql*a+frac{15l^2}{2}+M-d*R_b=30+30-10-5R_b=0
Где a — расстояние до начала действия равномерно-распределенной нагрузки, d — расстояние до опоры b.
Из уравнения момента мы можем найти, чему равна сила реакции правой опоры:
Подставляем это значение в уравнение равновесия сил и получаем силу реакции первой опоры:
R_a+R_b=R_a+14=30, R_a=16

Для того, чтобы найти прогибы, нам надо составить уравнения момента для каждого участка. В нашем случае удобнее всего Теперь найдём функцию распределения момента для первого участия. Так как в точке a балка закреплена не жестко, момент в ней по условию равен нулю. В ней возникает только сила реакции опоры Ra=16.
Момент на первом участке будет зависеть от удаления от этой силы:

Для нахождения угла наклона это выражение надо проинтегрировать:
θ_{(I)}=frac{1}{I_zE}∫R_axdx=frac{R_ax^2}{2I_zE}+C
И ещё раз для получения прогиба:
y_{(I)}=frac{1}{I_zE}∫frac{R_ax^2dx}{2}+∫Cdx=frac{R_ax^3}{6I_zE}+Cx+D
Затем нам нужно найти геометрию балки на участке с равномерно-распределенной нагрузкой.

При этом, момент на этом участке будет зависеть от двух составляющих: от силы реакции Ra с первого участка и от нагрузки q.
M_{z_{(II)}}=f(R_a,x)+f(q,x)
Функция момента (Mz(I)=Ra*x=12x) возникающего от силы на первом участке будет справедлива и для нашего участка: момент по-прежнему будет равен произведению плеча на силу.
По мере того, как мы будем отступать от начала действия равномерно-распределенной нагрузки, момент будет увеличиваться по квадратичному закону (почему, можно прочитать в статье посвященной теореме Журавского) M(q)=qx’^2/2, где x’ — расстояние от начала приложения нагрузки.
Нам удобнее все расчёты проводить из одной точки, поэтому для второго участка x’=x-a, где a координата начала приложения нагрузки. Таким образом, уравнение момента на втором участке будет выглядеть так:
Mz_{(II)}=Ra*x-frac{q(x-a)^2}2=16x-frac{15(x-1)^2}2
Интегрируем чтобы найти наклон:
θ_{(II)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6)+C
И ещё раз, чтобы найти прогиб:
y_{(II)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32})
На следующем участке действие равномерно-распределенной нагрузки заканчивается. При этом, мы хотим чтобы q(x-a)2/2 в формуле осталась: всё-таки она вносит вклад в момент и геометрию стержня.
Чтобы эту небольшую проблему исправить, мысленно продолжим распределенную силу до конца конструкции, но приложим в противовес ей точно такую же, направленную в другую сторону:

Таким образом на следующий участок стержня (который начинается в точке b) дополнительно будет приложена распределенная нагрузка q, которая будет создавать момент M=q(b-x)2/2.
Суммарный момент для третьего участка будет равен:
Mz_{(III)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2
Ну и, соответственно, найти наклон и прогибы не составляет трудности:
θ_{(III)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6)+C
y_{(III)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32})+Cx+D
Четвёртый участок начинается в месте приложения момента и заканчивается на второй опоре.
Составляем уравнение момента:
Mz_{(IV)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2+10
Где c — расстояние от начала координат до места приложения момента, а x-c, расстояние между точкой, которую мы рассматриваем и местом приложения момента. В нулевой степени это выражение всегда равно единице, поэтому для уравнения момента это константа. Но после интегрирования это выражение становится важной частью уравнения наклона:
θ_{(IV)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))+C
А затем и уравнения прогиба:
y_{(IV)}=\frac{1}{Iz*E}∫(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32}+frac{M(x-c)^2}{2})+Cx+D

Остается вычислить константы интегрирования. На первой и последней опоре прогибы (т.е. вертикальные перемещения) будут равны нулю. Подставляем x=0 в уравнение первого отрезка:
y_{(I)}=frac{R_a0^3}{6I_zE}+C*0+D
И выясняем, что константа интегрирования D равна нулю.
Подставляя константу интегрирования D в уравнение последнего участка для закрепленного конца балки (т.е. x=l=5) мы получим следующее уравнение:
0=frac{1}{Iz*E}*(frac{16*5^3}6-frac{15(5-1)^4}{32}+frac{15(5-3)^4}{32}+frac{10(5-4)^2}{2})+С*5+0
Выражение равно нулю по причине того, что прогибы в месте закрепления образовываться никак не могут.
Решив уравнение мы получим значение второй константы интегрирования:
С=frac{225,83}{5*Iz*E}=frac{45,17}{Iz*E}
Дальше остается лишь подставить эти константы в уравнения и мы получим уравнения наклонов и прогибов.

Итак, мы выяснили по каким законам будет прогибаться каждый участок балки.
Если резюмировать, то для получения уклона и прогиба на некотором участке, нам нужно просуммировать все воздействия и их проинтегрировать.
Метод начальных параметров
В общем виде углы наклона будут считаться так:
А прогибы так:
Примечание: не забывайте компенсировать равномерно-распределенную нагрузку в точке, где она заканчиваться!
На практике гораздо целесообразнее считать момент, наклон и прогиб сразу для всей балки, с помощью трех систем уравнений: системы моментов, наклонов и прогибов.
Уравнения моментов для каждого участка
Так их удобнее составлять, так как достаточно просто для каждого нового участка добавлять воздействия:
Уравнения наклонов
Как можно заметить, для того, чтобы из системы уравнений моментов получить систему уравнений наклонов достаточно проинтегрировать каждый член и добавить константу интегрирования C:
Уравнения прогибов
Как ни странно, для того, чтобы их получить, достаточно проинтегрировать каждый из членов уравнения наклона, добавить ещё одну константу интегрирования D, а первую константу C умножить на x.
Итак, подошёл к концу разговор о том, как материалы противодействуют изгибам. В прошлых частях мы уже выяснили, какие нормальные напряжения возникают в материале при попытке его согнуть. Обсудили и как с распределением момента связаны поперечные силы и касательные напряжения. А сейчас выяснили и как будет материал менять свою форму под воздействием изгиба.
Это имеет далекоидущие последствия для всех инженерных дисциплин и опирающихся на них специальностей. Например, ротор турбин, являющийся по своей сути длинным стержнем на опорах, под силой тяжести достаточно сильно изгибается. По этой причине для всех турбин большой мощности противопоказан быстрый старт. Перед тем, как соединять статор и ротор, стержень турбины необходимо повращать, чтобы он избавился от изгибающих деформаций. Иначе лопатки будут цепляться и в лучшем случае деформироваться, а в худшем ломаться. Но это уже совсем другая история.
В следующей части мы поговорим о другом виде воздействия момента на стержень: о кручении.
Автор: К.А.Овчинников
Редактор: Сабуров Даниил
Эксперт: Ершов Марк
За консультативную поддержку по математической части огромная благодарность Гришиной Ольге Андреевне, старшему преподавателю кафедры высшей математики БГТУ ВОЕНМЕХ.
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники:
- Горбатовский Александр Александрович Дифференциальное уравнение изогнутой оси балки // Курс лекций по сопротивлению материалов МГТУ ИМ. Н.Э.БАУМАНА
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова
- http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi
- https://spravochnick.ru/matematika/krivizna_krivoy/krivizna_i_ee_vychislenie/
- iSopromat Метод начальных параметров. Расчет перемещений сечений балки // https://youtu.be/xRp-ViFUl7Y
4 133
Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.
Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.
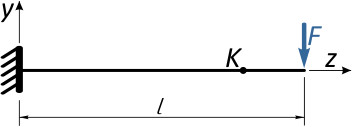
Рассмотрим на примере простой консольной балки.
Линейные перемещения
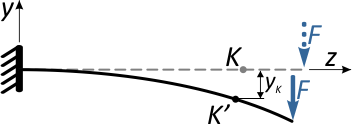
Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.
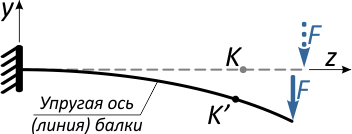
Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.
Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (yK)
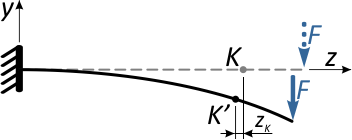
и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — zK
Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае zK<< yK), поэтому ими пренебрегают, ограничиваясь вычислением прогибов.
Линейные перемещения (прогибы балки) измеряются в метрах или кратных единицах измерения (миллиметрах и сантиметрах).
Прогибы, при которых сечение в результате деформации балки перемещается вверх принимаются положительными.
Именно по величине прогибов определяется жесткость балки.
Угловые перемещения
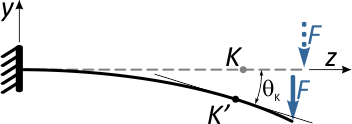
Кроме линейных, сечения балки при изгибе получают и угловые перемещения.
Проведем касательные к продольной оси балки в точках K и K’.
В первом случае линия касательной совпадает с прямой осью балки, во втором – располагается под углом θ.
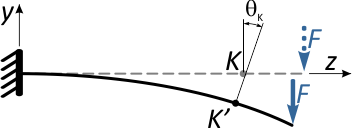
Угол между касательными очевидно равен углу между нормалями к оси балки в этих точках.
Этот угол θK называется углом наклона сечения K в результате деформации балки.
Вычисляется в радианах, с последующим переводом в градусы.
Между линейными и угловыми перемещениями при изгибе существует дифференциальная зависимость.
Например, в сечениях, углы наклона которых равны нулю следует ожидать экстремума изогнутой линии балки на данном участке.
Методы расчета перемещений
Существует несколько способов расчета линейных y и угловых θ перемещений при изгибе:
Метод начальных параметров (МНП)
Перемещения рассчитываются по уравнениям МНП
Считается относительно простым методом расчета перемещений в прямых балках с постоянной жесткостью сечения.
Данный способ не применим для расчета прогибов и углов наклона в балках переменного сечения, с изогнутой или ломаной осью и в рамах.
Подробнее >>
Интеграл Мора
Интеграл Мора относится к энергетическим методам расчета перемещений.
В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>
Способ Верещагина
Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.
Подробнее >>
Метод интегрирования дифференциального уравнения упругой линии балки
Непосредственное интегрирование дифференциального уравнения упругой линии
является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.
По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.
Эти вычисления и построения необходимы для проверки балок на жесткость.
Примеры решения задач >
Лекции по сопромату >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
6.1. Понятие об упругой
линии. Прогиб и угол поворота.
Дифференциальное уравнение упругой
линии. Условие жесткости при изгибе
Чтобы судить о работе изгибаемых балок,
недостаточно знать только напряжения,
которые возникают в сечениях балки от
заданной нагрузки. Вычисленные напряжения
позволяют проверить прочность системы.
Однако весьма прочные балки могут
оказаться непригодными к эксплуатации
из-за недостаточной жесткости. Если
балка при нагружении сильно прогибается,
то при эксплуатации сооружения, имеющего
гибкие балки, появятся затруднения и,
кроме того, могут возникнуть колебания
балки с большими амплитудами, а вместе
с тем и значительные дополнительные
напряжения.
Под жесткостью
следует понимать способность
элеменов конструкций и деталей машин
сопротивляться внешним нагрузкам без
видимых деформаций.
Расчет на жесткость заключается в оценке
упругой податливости балки под действием
приложенных нагрузок и подбор таких
размеров поперечного сечения, при
которых перемещения не будут превышать
установленных нормами пределов. Для
выполнения такого расчета необходимо
научиться вычислять перемещения сечений
балки под действием любой внешней
нагрузки.
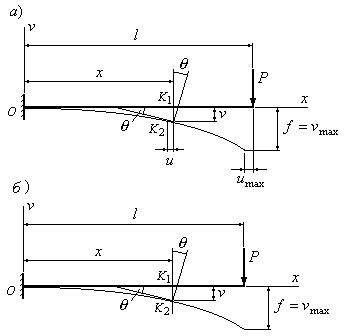
Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.
Точка
,
лежащая на оси в сечении, отстоящем не
расстоянииот начала координат, переместится в
точку.
Обозначим перемещение произвольной
точки оси бруса в направлении осичерез
,
а перемещение вдоль оси бруса – через.
Если в точкепровести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол.
Одновременно на тот же угол повернется
сечение в точке.
Таким образом, три величины
,
и
являются компонентами перемещения
произвольного поперечного сечения
балки. Перемещениецентра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
.
Угол
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью.
Рис.6.1
Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб
не должен превышать определенной доли
пролета:
.
Число
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величинапринимается равной 1000.
Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:
.
(6.1)
Во-вторых, горизонтальными
перемещениями
можно пренебречь, так как они существенно
меньше(
).
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.
Для определения полной картины деформаций
необходимо получить уравнение упругой
линии
.
Исходя из физической природы изогнутой
оси бруса, можем утверждать, что упругая
линия должна быть непрерывной и гладкой
кривой, следовательно, на протяжении
всей оси бруса должны быть непрерывны
функция и ее первая производная. Прогибы
и углы поворота и являются перемещениями
сечений балок при изгибе. Деформация
того или иного участка балки определяется
его кривизной.
При выводе формулы для нормальных
напряжений при изгибе нами была получена
связь между кривизной и изгибающим
моментом:
.
(6.2)
Из курса высшей математики известно
следующее уравнение кривизны плоской
кривой:
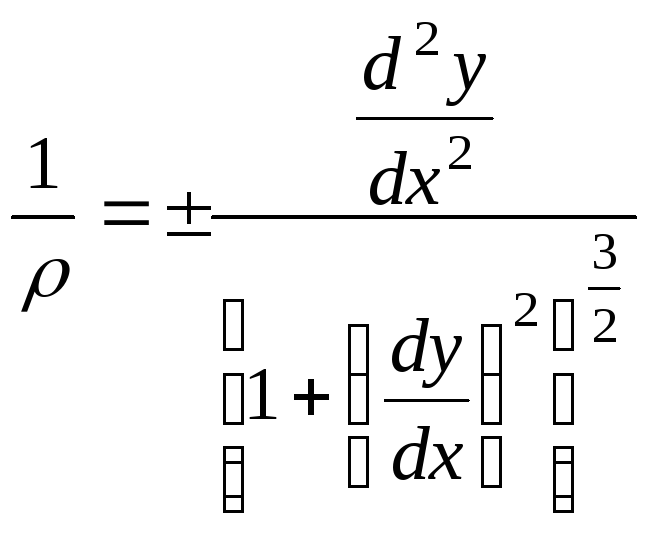
(6.3)
Подставляя значение
кривизны в равенство (6.2) и заменяя
координату
прогибом
,
получим точное дифференциальное
уравнение упругой линии балки:
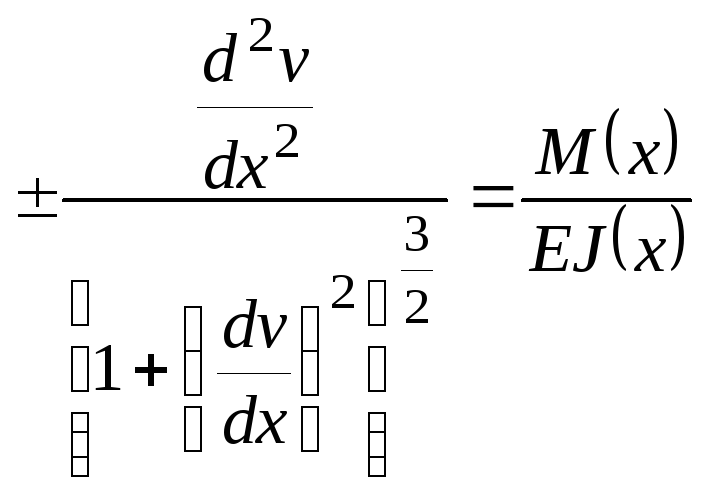
(6.4)
Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона
касательной к оси будут малы, квадратом
первой производнойпо
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение
(6.5)
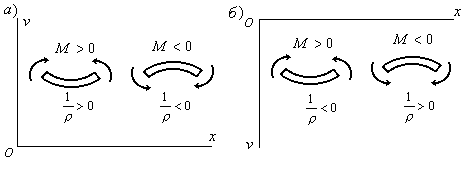
Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны
может не совпадать со знаком изгибающего
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
растянутые волокна. Так, например, для
случая, когда осьнаправлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.
Рис
6.2
Таким
образом, в случае, когда ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.
6.2. Метод непосредственного
интегрирования приближенного (основного)
дифференциального уравнения упругой
линии
Решая
задачу аналитическим методом, углы
поворота
и прогибы
вычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота:
,
(6.6)
где
постоянная интегрирования.
Интегрируя
второй раз, получим выражение для прогиба
:
,
(6.7)
где
и
постоянные интегрирования.
Для
вычисления интегралов, входящих в (6.6)
и (6.7), необходимо сначала написать
аналитические выражения для изгибающего
момента и жесткости. Постоянные
интегрирования находятся
из граничных условий,
которые зависят от условий перемещения
границ участков балки.
Рассмотрим несколько
примеров применения метода непосредственного
интегрирования приближенного уравнения
упругой линии балки.
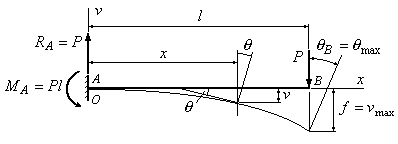
Пример
6.1. Определить
стрелу прогиба и угол поворота сечения
В балки, изображенной на рис.6.3.
Рис.6.3
Решение:
1. Из условий
равновесия определяем опорные реакции:
;
.
2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.
3.
Составляем уравнение изгибающего
момента в сечении
:
.
4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Интегрируем
уравнение первый раз. Получаем:
.
(а)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:
.
(б)
Так как в заделке прогиб и угол поворота
равны нулю, то для определения постоянных
интегрирования граничные условия имеют
вид:
при
;
при.
Из
уравнения (а) видно, что постоянная
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а),
находим.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
,
получаем.
Таким образом,
получаем следующие выражения для прогиба
и угла поворота:
,
.
Подставляя
в первое уравнение
,
найдем стрелу прогиба:
.
Подставляя
во второе уравнение
,
найдем максимальный угол поворота
.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.
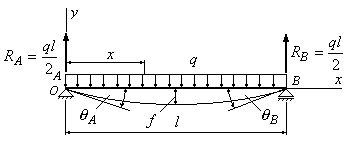
Пример
6.2. Определить
стрелу прогиба двухопорной балки и углы
поворота опорных сечений А и В (рис.6.4).
Рис.6.4
Решение:
1. Из условий
равновесия определяем опорные реакции:
.
2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
вправо.
3.
Составляем уравнение изгибающего
момента в сечении
:
.
4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Интегрируем
уравнение первый раз. Получим:
.
(в)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:
.
(г)
Постоянные
интегрирования найдем из граничных
условий:
при
;
при.
Подставляя
в уравнение (г)
и приравнивая прогиб нулю, получим
;
подставляя в это же уравнение,
находим постоянную интегрирования:
.
Найденные значения
постоянных интегрирования подставим
в уравнения (в) и (г) и получим уравнения
углов поворота и прогибов:
;
.
Подставляя
и
в первое уравнение, получим углы поворота
соответственно сечений А и В:
;
.
В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение
,
получим:
.
Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение В повернулось
против часовой стрелки.
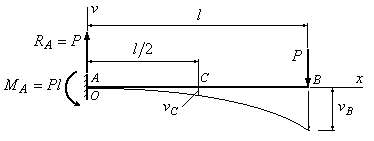
Пример
6.3. В сколько
раз прогиб в сечении В на конце изображенной
на рис.6.5 балки, больше, чем прогиб в
сечении С
посредине
балки?
Рис.6.5
Решение:
Воспользуемся
результатами, полученными в примере
6.1. Запишем окончательное выражение для
прогиба:
и подставим в это
уравнение координаты точек С и В. Получим:
при
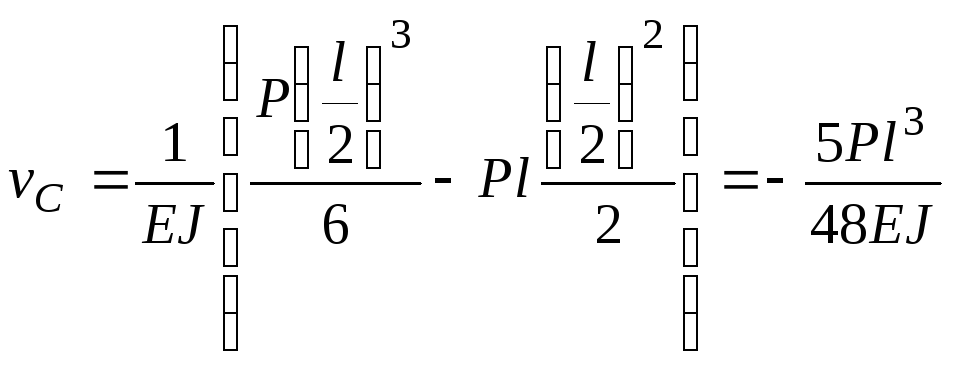
при
.
Сравнивая полученные
величины прогибов, приходим к выводу,
что прогиб в сечении В больше, чем прогиб
в сечении С в 3,2 раза:
.
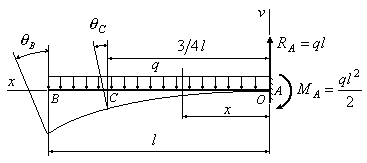
Пример
6.4. В сколько
раз угол
поворота сечения
А
на конце изображенной на рис.6.6 балки
больше, чем угол поворота сечения В на
расстоянии четверти пролета от левого
конца балки?
Решение:
1.
Находим реакции: ;
.
2.
Выбираем начало координат
на правом конце балки, совмещая его с
точкой А. Осьнаправляем вверх, ось
влево.
Рис.6.6
3.
Записываем выражение для изгибающего
момента в сечении
:
.
4. Составляем приближенное дифференциальное
уравнение упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Принимаем жесткость балки постоянной.
Интегрируем дифференциальное уравнение.
Получаем:
.(д)
Постоянную интегрирования
в уравнении (д) найдем из условия, что
приугол поворота в сечении А равен нулю.
Подставим в уравнение (д)и приравняем нулю угол поворота сечения
А. Получим.
Тогда окончательно уравнение для угла
поворота принимает вид:
.(е)
6.
Подставляем в уравнение (е) координату
,
получим угол поворота в сечении С:

7.
Подставляем в уравнение (е) координату
.
Получим угол поворота в сечении В:
.
8. Сравнивая углы
поворота в сечениях В и С, получим:
.
Таким образом,
угол поворота в сечении В в 1,016 раза
больше, чем угол поворота в сечении С.
Пример
6.5.
Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна
кНм2.
Рис.6.7
Решение:
Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении
:
.
(ж)
Постоянные
интегрирования в уравнении (ж) получим,
воспользовавшись граничными усорвиями
закрепления балки, в соответствии с
которыми прогиб и угол поворота в жесткой
заделке равны нулю:
при
и
.
Подставляя
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:;
.
Тогда выражение для прогиба принимает
вид:
.
Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба (),
находим:
м
мм.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #