Египетский треугольник
В математике есть определенные каноны, которые явились, так сказать, фундаментом или основанием всего последующего развития современной математики. Одним из этих канонов, по праву можно считать теорему Пифагора.
Кому еще со школьных времен не известна смешная формулировка теоремы Пифагора: “Пифагоровы штаны во все стороны равны”. Ну да, правильно это звучит так: “квадрат гипотенузы равен сумме квадратов катетов “, но про штаны гораздо лучше запоминается.
Нагляднее всего это видно на треугольнике со сторонами 3-4-5. Но если изучить внимательно использование такого треугольника в древней истории, то можно заметить одну занимательную вещь и называется она ни как по другому, как Египетский треугольник.
Этот самый философ и математик Пифагор Самосский из Греции, именем которого и названа эта теорема, жил примерно 2,5 тысяч лет тому назад. Ну конечно дошедшая до нашего времени биография Пифагора не совсем достоверна, но, тем не менее, известно что Пифагор много путешествовал по странам Востока. В том числе он был и Египте и Вавилоне. В Южной Италии Пифагор основал свою знаменитую “Пифагорову школу”, которая сыграла очень даже важную роль, как в научной, так и политической жизни древней Греции. С тех времен по преданиям Плутарха, Прокла и других известных математиков того времени, считалось, что эта теорема до Пифагора известна не была и именно по этому её назвали его именем.
Но история говорит что это не так. Обратимся туда, где бывал Пифагор и что видел, прежде чем сформулировать свою теорему. Африка, Египет. Бесконечный и однообразный океан песка, почти ни какой растительности. Редкие кустики растений, едва заметные верблюжьи следы. Раскаленная пустыня. Солнце и то кажется тусклым, как будто покрытым этим вездесущим мелким песком.
И вдруг, как мираж, как видение, на горизонте возникают строгие очертания пирамид, изумительных по своим идеальным геометрическим формам, устремленным к палящему солнцу. Своими огромными размерами, и совершенством своих форм они изумляют.
Скорее всего, Пифагор их видел в ином виде, нежели как они выглядят сейчас. Это были сияющие полированные громады с четкими гранями на фоне многоколонных прилегающих храмов. Рядом с величественными царскими пирамидами стояли пирамиды поменьше: жен и родичей фараонов.
Власть фараонов Древнего Египта была непререкаемой. Фараонов считали божеством и отдавали им божественные почести. Фараон-бог был вершителем судьбы народа и его покровителем. Даже после смерти культ фараона имел преогромное значение. Умершего фараона сохраняли веками, и для сохранения тела фараона сооружали гигантские пирамиды. Величие, архитектура и размеры этих пирамид поражают и сейчас. Недаром эти сооружения относили к одному из семи чудес света.
Изначально назначение пирамид было не только как усыпальниц фараонов. Считают что они сооружались как атрибуты могущества, величия, и богатства Египта. Это памятники культуры того времени, хранилища истории страны и сведений о жизни фараона и его народа, собрание предметов быта того времени. Кроме того однозначно, что пирамиды имели определенное “научное содержание”. Их ориентирование на местности, их форма, размеры и каждая деталь, каждый элемент настолько тщательно продумывались, что должны были продемонстрировать высокий уровень знаний создателей пирамид. Очевидно что они строились на тысячелетия, “навечно”. И недаром арабская пословица гласит: “Все на свете страшится времени, а время страшится пирамид”.
Своим аналитическим умом Пифагор не мог не заметить определенную закономерность в формах и геометрических размерах пирамид. Скорее всего, это и натолкнуло Пифагора на анализ этих размеров, что впоследствии и было им выражено своей знаменитой теоремой, от которой ныне и отталкивается современная геометия.
Среди множества пирамид сохранившихся до нашего времени особое место занимает пирамида Хеопса. Если рассмотреть геометрическую модель этой пирамиды и восстановить её первоначальную форму, то очевидно, что её поперечное сечение представляет собой два треугольника с внутренним углом равным 51°50′.
Сейчас пирамида является усеченной, но это разрушения времени, а если геометрически восстановить её в первоначальном виде, то получается что стороны этих треугольников равны: основание СВ = 116, 58 м, высота АС = 148,28 м.
Отношение катетов у/х = 148,28/116,58 = 1,272. А это величина тангеса угла 51град 50 мин. Получается, что в основу треугольника АСВ пирамиды Хеопса было заложено отношение AC/CB = 1,272. Такой прямоугольный треугольник называется “золотым” прямоугольным треугольником.
Получается что основной “геометрической идеей” пирамиды Хеопса является “золотой” прямоугольный треугольник. Но особой в этом отношении является пирамида Хефрена. Угол наклона боковых граней у этой пирамиды равен 53°12, при котором отношение катетов прямоугольного треугольника 4:3. Такой треугольник называют “священным” или “египетским” треугольником. По мнению многих известных историков, “египетскому” треугольнику в древности придавали особый магический смысл. Так Плутарх писал, что египтяне сопоставляли природу Вселенной со “священным” треугольником: символически они уподобляли вертикальный катет мужу, основание – жене, а гипотенузу – тому, что рождается от обоих.
Для египетского треугольника со сторонами 3:4:5 справедливо равенство: 32 + 42 = 52, а это и есть знаменитая теорема Пифагора. По неволе напрашивается вопрос: не это ли соотношение хотели увековечить египетские жрецы, построив пирамиду в основе которой лежит треугольник 3:4:5. Пирамида Хефрена наглядное подтверждение того что знаменитая теорема была известна египтянам задолго до ее открытия Пифагором.
Неизвестно как это попало к древним египтянам, то ли это заслуга их ученых, то ли это дар из вне, не исключается и то, что это дар внеземной цивилизации, но использование такого треугольника давало египетским строителям очень существенную и к тому же простую возможность при возведении таких огромных сооружений соблюдать точные геометрические размеры. Ведь свойства этого треугольника таковы, что его угол между катетами является равный 90 градусов. То есть использование такого элемента позволяет обеспечить точную перпендикулярность сопрягаемых элементов и естественно всей конструкции, что и подтверждает архитектура древнего Египта.
Получить прямой угол без необходимых инструментов не просто. Но если воспользоваться этим треугольником, оказывается все достаточно просто. Нужно взять обычную веревку, разделить её на 12 равных частей, и из них сложить треугольник, стороны которого будут равны 3, 4 и 5 частям. Угол между сторонами длиной 3 и 4 части оказывается и есть прямой. Вот это и есть Египетский треугольник Пифагора.
Во многих исторических письменах имеются следы, что уникальные свойства “египетского треугольника” были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.
Знаменитая древнеегипетская пословица “Делай, как делается”, дошедшая до наших дней, наталкивает на мысль что сами египтяне, возводившие эти строительные шедевры, были простыми исполнителями и особыми знаниями не обладали, а все секреты были скрыты от непосвященных. Ведь работами на строительстве руководили жрецы – члены особой привилегированной замкнутой касты. Они были хранителями древних знаний, которые держались в секрете. Но пытливый ум великого мыслителя Пифагора сумел разгадать один их этих секретов.
Умы людей всегда будоражат разнообразные загадки, и это, вероятно, будет всегда. Египетский треугольник, хоть и известен человечеству с незапамятных времён, все-таки одна из не полностью разгаданных тайн.
Ведь, что не говори, а форма египетского треугольника и проста, и в то же время гармонична, по своему он даже красив. И с ним достаточно легко работать. Для этого можно использовать самые простые инструменты – линейку и циркуль. Использую этот незатейливый элемент и его симметричные отображения, можно получить красивые, гармоничные фигуры. Это и мальтийский крест, и серединное сечение пирамиды Хефрена, и фрактальный ряд убывающих – возрастающих, по размерам египетских треугольников в соответствии с правилом золотого сечения. Это удивительное богатство гармоничных пропорций.
До сих пор в мире есть много пытливые люди, которые как безумцы изобретают вечный двигатель, ищут квадратуру круга, философский камень и книгу мёртвых. Скорее всего, усилия их тщетны, но даже в случае с Египетским треугольником, ясно что “простых тайн” на земле еще много.
Теорема Пифагора

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c 2 − b 2
- b = √c 2 − a 2
- c = √a 2 + b 2
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
- если c 2 2 + b 2 , значит угол, противолежащий стороне c, является острым.
- если c 2 = a 2 + b 2 , значит угол, противолежащий стороне c, является прямым.
- если c 2 > a 2 +b 2 , значит угол, противолежащий стороне c, является тупым.
Записывайтесь на курсы обучения математике для школьников с 1 по 11 классы!
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a 2 + b 2 = c 2 .
Пошаговое доказательство:
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a 2 = c * HB, b 2 = c * AH.
- Сложим полученные равенства:
a 2 + b 2 = c * HB + c * AH
a 2 + b 2 = c * (HB + AH)
a 2 + b 2 = c * AB
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁ 2 = A₁C₁ 2 + B₁C₁ 2 .
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
Пусть катеты a = 6 и b = 8.
По теореме Пифагора c 2 = a 2 + b 2 .
Подставим значения a и b в формулу:
c 2 = 6 2 + 8 2 = 36 + 64 = 100
c = √100 = 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
Ответ: треугольник не является прямоугольным.
Прямоугольный треугольник. Теорема Пифагора.
теория по математике 📈 планиметрия
Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.
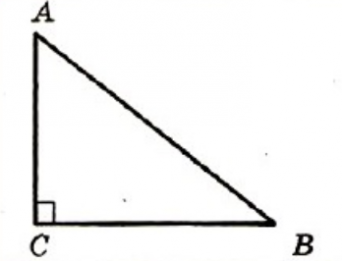
На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.
Свойства прямоугольного треугольника
- В прямоугольном треугольнике гипотенуза является наибольшей стороной.
- В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .
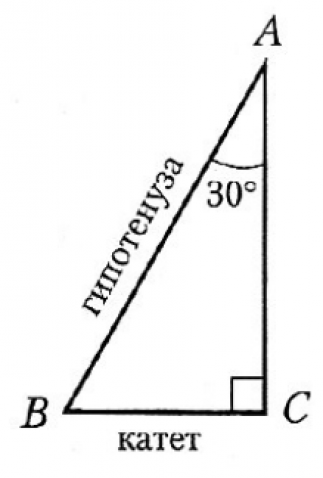
Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .
- Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
- Медиана, проведенная к гипотенузе, равна её половине.
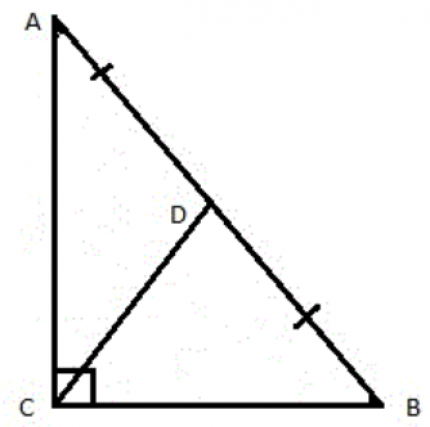
На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.
Признаки равенства прямоугольных треугольников
Существует 4 признака равенства прямоугольных треугольников:
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:
- по катетам;
- по катету и прилежащему острому углу;
- по гипотенузе и острому углу;
- по гипотенузе и катету.
Теорема Пифагора
Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
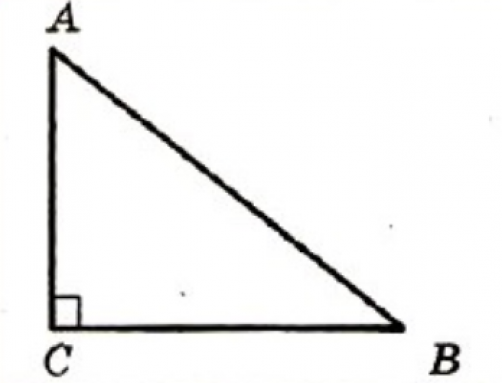
На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2
Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.
Египетский треугольник
Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.
Пифагоровы тройки
Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/teorema-pifagora-formula
[/spoiler]
План урока:
Теорема Пифагора
Задачи на применение теоремы Пифагора
Пифагоровы тройки
Обратная теорема Пифагора
Формула Герона
Теорема Пифагора
Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.
Изучим центральную фигуру, чью площадь мы обозначили как S2. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.
Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.
На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.
Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.
Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.
Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.
Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х2. Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.
Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с2– это площадь большого (на рисунке – синего)квадрата, а х2 – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:
10:2 = 5
Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора
Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.
Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.
Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.
Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.
Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.
Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки
Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.
Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.
Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.
Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.
Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.
Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.
Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а2, b2 и с2 – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а2 + b2 четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.
Обратная теорема Пифагора
По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А1В1С1 прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.
Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:
1) некоторое условие, которое описывает какое-то геометрическое построение;
2) вывод (или заключение), который делается для условия.
В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.
В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.
Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.
Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона
Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.
Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h2:

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.
Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?
Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.
Пифагор ((570)–(490) года до н. э.) – древнегреческий математик, мыслитель и философ.

Рис. (1). Пифагор.
Факты биографии Пифагора достоверно не известны. О его жизненном пути можно судить лишь по произведениям других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учёными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.
Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и учёного было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.

Рис. (2). Теорема Пифагора.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами (3), (4) и (5) является прямоугольным.
В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):

Рис. (3). Прямоугольный треугольник.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c2=a2+b2
.
Известны очень многие доказательства теоремы разными математическими методами, но одни из самых наглядных связаны с площадями.
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника
a+b
. Площадь квадрата равна
a+b2
:

Рис. (4). Первое доказательство теоремы Пифагора.
2. Если провести гипотенузы (c), очевидно, что они образовали квадрат внутри построенного квадрата.
Стороны четырёхугольника равны (c), а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают
90°
, то угол четырёхугольника также равен
90°
, потому что вместе все три угла дают
180°
.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.

Рис. (5). Второе доказательство теоремы Пифагора.
3. На двух сторонах квадрата поменяем местами отрезки (a) и (b), при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами (a) и (b), и двух площадей прямоугольников:

Рис. (6). Третье доказательство теоремы Пифагора.
4. Из этого следуют выводы:
c2+4⋅ab2=(a+b)2;c2+2ab=a2+2ab+b2;
Обрати внимание!
Если находим длину гипотенузы (c), то выполняем сложение квадратов длин катетов (a) и (b) и определяем квадратный корень:
c2=a2+b2;c=a2+b2.
Если находим длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:
a2=c2−b2;a=c2−b2.
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
является ли треугольник со сторонами (6) см, (7) см и (9) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник не прямоугольный.
Является ли треугольник со сторонами (5) см, (12) см и (13) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник прямоугольный.
Чтобы не тратить много времени на решение, полезно запомнить наиболее часто используемые числа Пифагора:
катет, катет, гипотенуза
(3), (4), (5);
(6), (8), (10);
(12), (16), (20);
(5), (12), (13).
Посмотри ещё одно своеобразное доказательство теоремы Пифагора:

Рис. (7). Четвёртое доказательство теоремы Пифагора.
Источники:
Рис. 2. Теорема Пифагора. Указание авторства не требуется, 2021-06-05, Наука/Технологии, бесплатно для коммерческого использования, https://clck.ru/VK55r.
Рис. 4, 5, 6. Доказательства теоремы Пифагора, © ЯКласс.
Рис. 7. Четвёртое доказательство теоремы Пифагора, http://linguaggio-macchina.blogspot.com
Все статьи из цикла “В чем прелесть предмета”
Другие статьи из цикла “В чем прелесть математики”:
Визуальные доказательства
Теорема Байеса
Красота рассуждений
Режем провода
Прятки с геометрией
Бесконечность
Математика не только формулы. Математика – это все, что нас окружает. В ней важно не только знать теоремы и аксиомы, но и понимать, чувствовать ее фундаментальные принципы. К одному из таких фундаментальных знаний можно отнести теорему Пифагора, с которой мы знакомимся еще в школе на уроках геометрии. Однако, как порой это бывает, учебная программа упускает красоту и изящество самой теоремы, чья роль намного важнее, чем нахождение сторон треугольника; теорема Пифагора находит неисчисляемое множество применений в науке и технике – невозможно переоценить ее значимость.
В этой статье мы познакомимся с историей теоремы Пифагора, узнаем, как чертили прямые углы в Древнем Египте, что такое пифагоровы тройки и какой магией обладает математика, спрятанная в простой теореме о сумме квадратов катетов.
История теоремы Пифагора
Теорема Пифагора:
В любом прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. [c^2=a^2+b^2 ]
Несмотря на то, что сейчас имя Пифагора навсегда связано с теоремой о квадратах катетов и гипотенузы, мы не имеем никаких сохранившихся письменных свидетельств того, что сам Пифагор открыл и доказал эту теорему. И хотя некоторые авторы античных времен в лице Плутарха и Цицерона считали, что теорему вывел именно Пифагор, первооткрывателем его не назовешь. Что мы знаем наверняка – теорема принадлежит древнейшему периоду пифагорейской математики между VI веком до н. э. и V веком н. э.
Одна скромная глиняная дощечка, найденная археологами XX века в Месопотамии, также выступает против первенства древнегреческого математика. Она наглядно показывает, что теорема могла быть открыта вавилонскими математиками за (1000) лет до рождения самого Пифагора.
Эта глиняная табличка, известная как Plimpton 322, датируется примерно XIX-XVI веком до нашей эры. На ней перечислены пятнадцать троек с длинами отрезков, образующих прямоугольный треугольник: ((3, 4, 5)), ((28, 45, 53)) и (65, 72, 97)), но не ((5, 12, 13)) или ((8, 15, 17)), хотя присутствует даже тройка ((12 709, 13 500, 18 541))! Получить подобные тройки простым подбором практически невозможно, поэтому ученые предполагают, что автор дощечки знал, как получить больше подобных троек из формулы Пифагора, которая была открыта спустя 1000 лет. Кроме того, Plimpton 322 была написана в том же формате, что и другие административные (не математические) документы того периода. Упоминание пифагоровых троек в подобном “общественном” документе показывает, что теорема Пифагора не являлась математическим открытием для жителей Междуречья, а активно применялась в жизни вавилонян.
На сегодняшний день известно, что задачи и факты, связанные теоремой Пифагора, встречаются и в древнеиндийском трактате VII–V вв. до н.э. «Сульва Сутра», и древнекитайском сочинении «Чжоу-би Суань Цзинь» III–I вв. до н. э., а также в египетских источниках времен фараона Аменемхета I (2300 г. до н.э). Удивительно, как теорема Пифагора занимала умы математиков с древнейших времен. Чего же стоят около 370 разнообразных доказательств, существующих в наши дни!
Доказательство теоремы
В количестве доказательств с теоремой Пифагора не может соревноваться ни одно из существующих математических утверждений. Первоначально, в 1927 году, все эти доказательства были собраны в одну большую книгу по математике и включали доказательство 12-летнего Альберта Эйнштейна, который воспользуется этой теоремой два десятилетия спустя для теории относительности, доказательства Леонардо да Винчи и двадцатого президента США Джеймса Абрам Гарфилда.
С одним из самых простых и красивых доказательств известной теоремы вы могли познакомиться в статье Визуальные доказательства из цикла “В чем прелесть математики”. Здесь же мы представим алгебраическое доказательство этой теоремы, используя один и тот же рисунок.
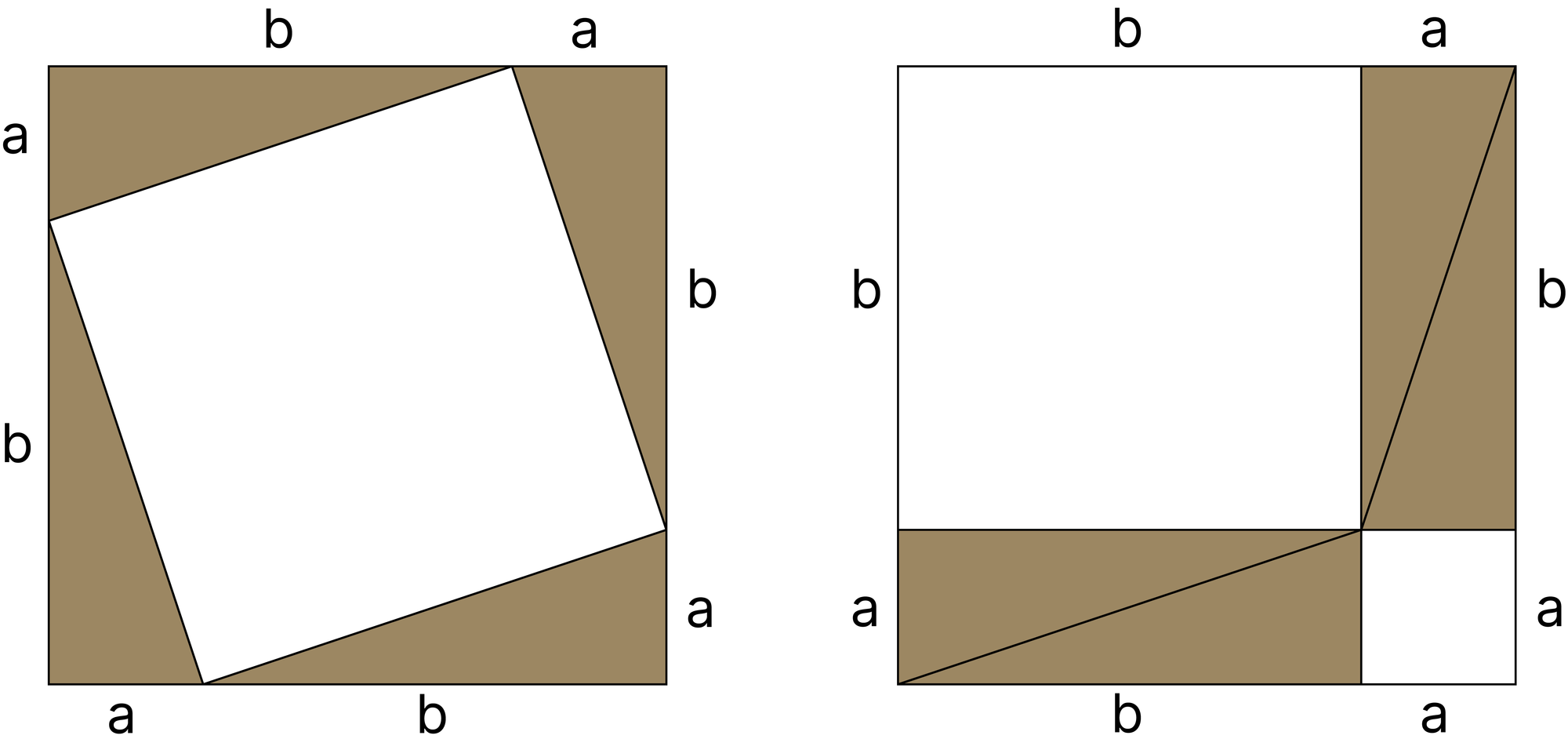
Нарисуем квадрат со стороной (a+b), а внутри – (4) прямоугольных треугольника с катетами (a), (b) и гипотенузой (c), расположенных так, как изображено на рисунке слева. Давайте посмотрим на площадь большого квадрата с разных точек зрения: с одной стороны, она равна ( (a+b)^2 ), а с другой, сумме площадей этих пяти частей. Площадь белого квадрата равна ( c^2 ), а каждая из четырех серых прямоугольных треугольников по ( frac{a cdot b}{2} ). Тогда [c^2+4 cdotfrac{a cdot b}{2} = (a+b)^2 =a^2+b^2 + 2ab.] [c^2+ 2ab = (a+b)^2 =a^2+b^2 + 2ab.] Таким образом, [c^2=a^2+b^2.] Теорема доказана!
Теорема работает и в обратную сторону: если для сторон треугольников выполняется известное (a^2+b^2 = c^2), то это непременно прямоугольный треугольник!
Пифагоровы тройки
Как начертить прямой угол? Сейчас ответ на этот вопрос кажется предельно очевидным: либо с помощью транспортира и линейки, либо достаточно тетради в клетку. А что делать строителю из Древнего Египта, не знающему ни о тетрадях, ни о транспортире? Он несомненно использовал бы теорему Пифагора (хотя и не называл бы ее именно так).
Чтобы начертить прямые углы, древние египтяне использовали треугольник (3-4-5), который по теореме Пифагора является прямоугольным. Сначала они брали веревку и делали на ней отметки, разбивающие веревку на (12) ((3+4+5=12)) равных частей, затем концы веревки связывались. После этого веревку растягивали в виде треугольника со сторонами (3-4-5). Получившийся угол между сторонами (3) и (4) оказывался прямым – то, что надо! Впоследствии именно этот треугольник со сторонами (3-4-5) был назван египетским треугольником – в честь своих первых пользователей.
Однако прямые углы можно чертить с помощью не только египетского, но и любого прямоугольного треугольника, чьи стороны удовлетворяют теореме Пифагора. Если стороны такого треугольника являются целыми числами, то их называют пифагоровыми тройками. Представим несколько таких троек:[3^2+4^2=5^2, 5^2+12^2=13^2, ] [8^2+15^2=17^2, , 9^2+12^2=15^2]Вы наверняка встречали их в жизни, особенно на контрольных по математике, когда учителя стараются составлять задачи с удобными целочисленными ответами.
Любопытно, что все пифагоровы тройки похожи друг на друга как братья. Давайте посмотрим, как получаются Пифагоровы тройки из одноименной теоремы. Вернемся к нашему уравнению и возьмем некую пифагорову тройку (a,b,c):[c^2=a^2+b^2]А теперь рассмотрим точно такой же треугольник, но со сторонами в два раза больше(2a,2b,2c). Тогда получим:[(2c)^2=(2a)^2+(2b)^2 Rightarrow 4c^2=4a^2+4b^2 Rightarrow c^2 = a^2+b^2.]Выходит, что эта бóльшая тройка, получившаяся из предыдущей поменьше, так же будет пифагоровой. Например, линейные величины треугольника (6-8-10) в (2) раза больше, чем у египетского треугольника (3-4-5). Умножив стороны на любое другое число, мы получим другие значения, которые образуют новые пифагоровы тройки. Так, треугольник (9-12-15) получается при увеличении египетского в (3) раза, а (150-200-250) – при увеличении в (50) раз. Такие тройки называются подобными, потому что они не отличаются по своим свойствам, за исключением масштаба, а исходная тройка, являющаяся основой для ряда пифагоровых троек, называется примитивной.
Обобщения теоремы Пифагора
В теоремах часто есть ограничения или условия, в рамках которых известная математикам формула будет выполняться. Сама теорема Пифагора верна только для прямоугольных треугольников и работает только на плоскости, то есть в двухмерном пространстве. А можно ли обойти эти условия? Как придумать более общие теоремы? На самом деле, эти вопросы являются основной заботой многих математиков-исследователей на протяжении столетий, ведь каждый раз нам приходится разрешать все новые ограничения. Чтобы помочь математикам вписать теоремы и формулы в новые отдаленные от конкретного примера условия, на помощь приходит один из методов математического творчества – обобщение. Так, у теоремы Пифагора, выполняющейся строго в прямоугольных треугольниках на плоскости, есть по крайней мере (2) обобщения.
Теорема косинусов
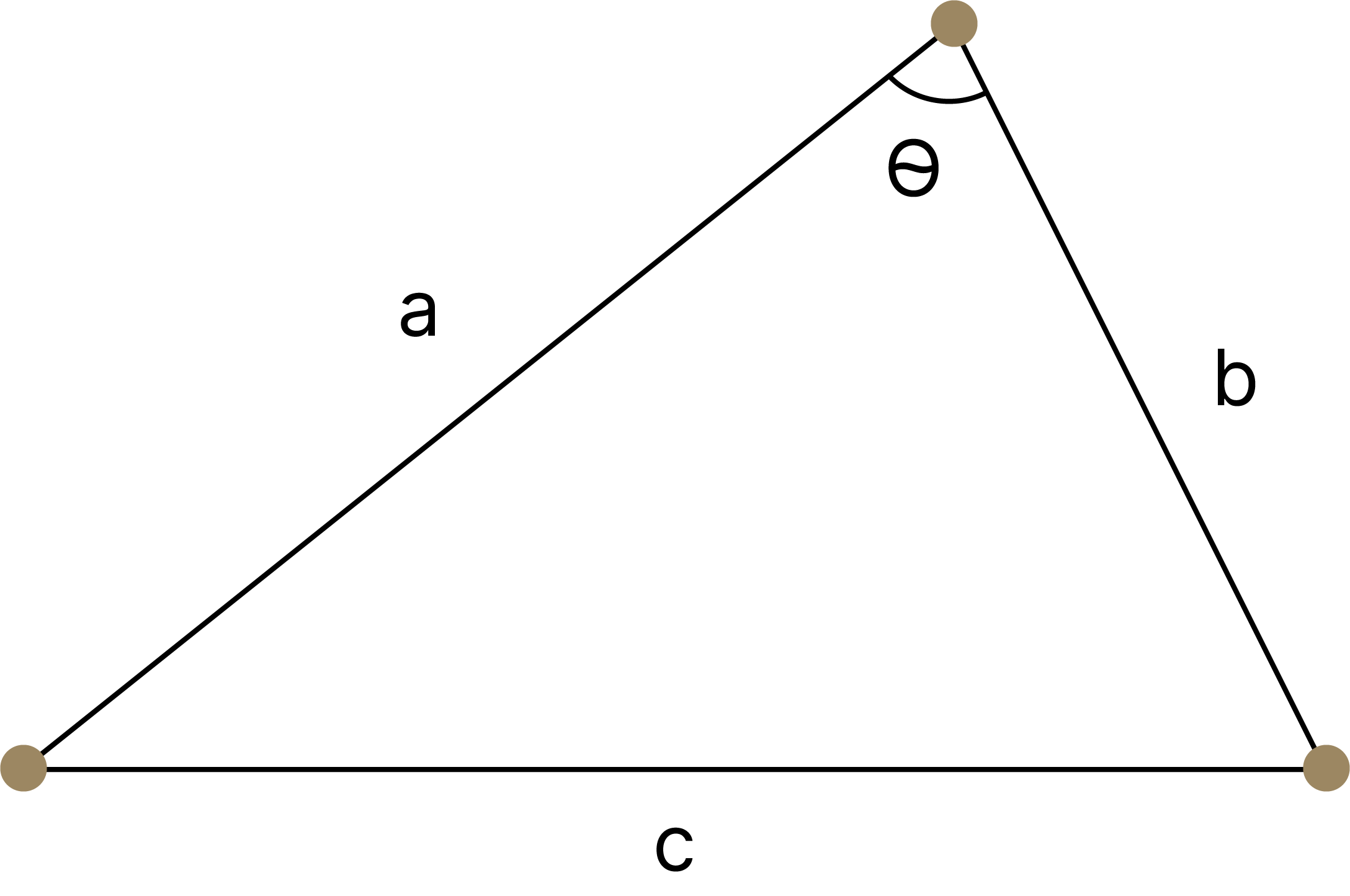
Первым естественным шагом при обобщении теоремы Пифагора является получение утверждения не только для прямоугольных треугольников, но и для всех других – тупоугольных и остроугольных. Как можно выразить одну сторону треугольника, когда мы знаем два другие стороны и угол между ними? Поможет теорема косинусов!
Мы можем выразить сторону (c), имея стороны ( a, b) и угол ( theta ) между ними, получив уравнение вида: [c^2= a^ 2 +b^2 – 2ab cdot cos{ theta} ]
Действительно, для прямоугольного треугольника, в котором угол ( theta = 90^{circ}), это утверждение приводит к теореме Пифагора, так как (cos{(90^{circ})} = 0), а значит [c^2= a^ 2 +b^2 – 2ab cdot cos{90^{circ} } = a^ 2 +b^2 – 2ab cdot 0 = a^ 2 +b^2 ]
Диагональ параллелепипеда
Когда прямоугольник расположен на плоскости, легко понять, как использовать теорему Пифагора, чтобы найти длину его диагонали: нужно провести диагональ, делящую прямоугольник на два равных прямоугольных треугольника, и затем найти длину диагонали (гипотенузу) по теореме Пифагора. Это обобщение действует в двухмерном пространстве. А можно ли перейти в наше трехмерное пространство?
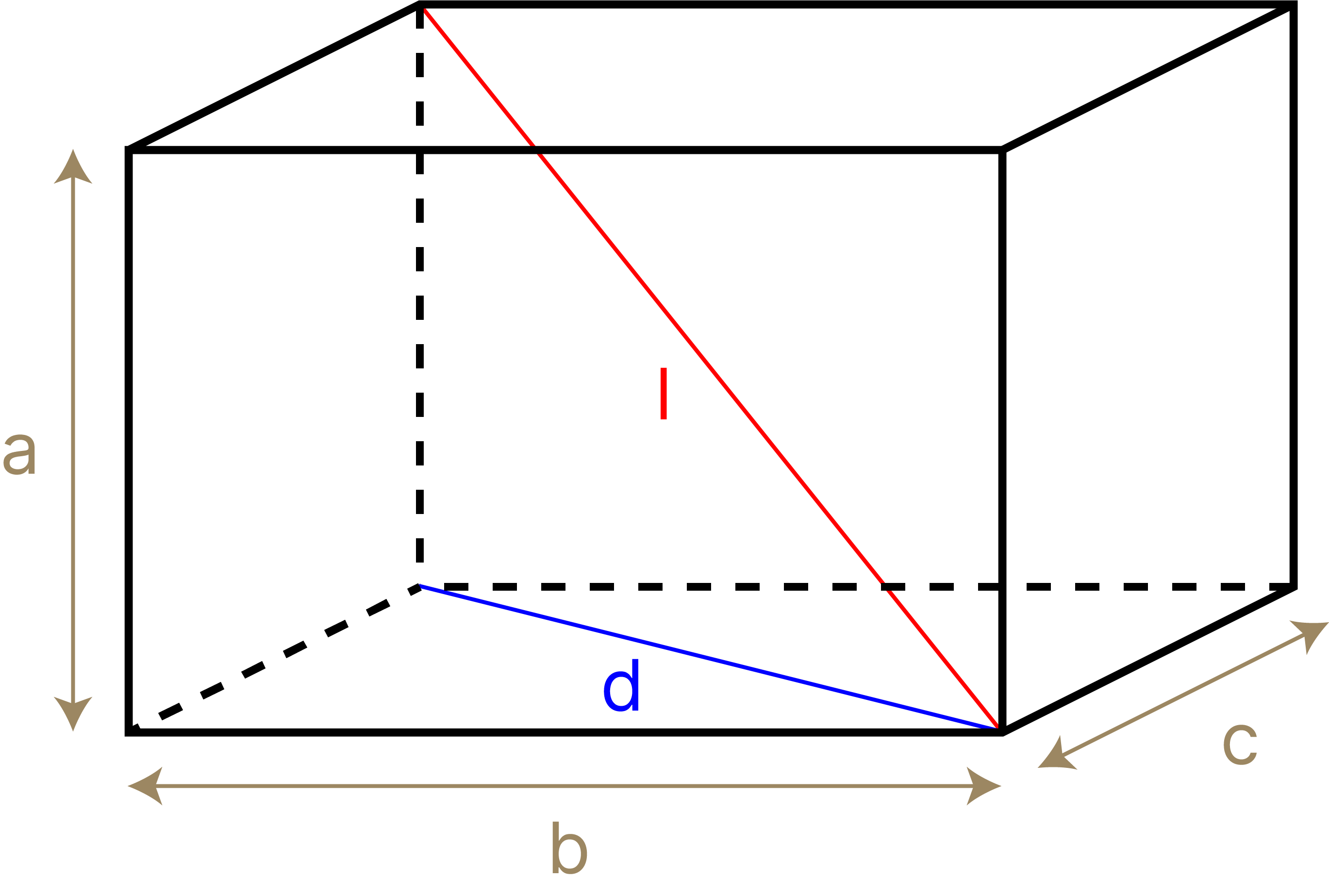
Возьмем диагональ параллелепипеда. Как можно найти ее длину? Оказывается, теорема Пифагора помогает и тут: чтобы найти диагональ, нам достаточно применить теорему два раза. Искомая диагональ параллелепипеда – красный отрезок, представленный на рисунке. Обозначим его длину как (l), а длину синего отрезка как (d). Можно заметить, что синий отрезок – это диагональ обычного прямоугольника в основании, у которого длины сторон равны (a) и (c). По теореме Пифагора мы получаем: [d^2 = a ^ 2 + c ^ 2 ] Теперь же мы можем рассмотреть треугольник, для которого красная диагональ является гипотенузой, а стороны – катетами (d) и (b). Тогда по теореме Пифагора мы получаем: [ l^2 = d ^ 2 + b^2] Вспомнив первое уравнение, полученное из треугольника в основании, мы можем переписать выражение как [ l^2 = d ^ 2 + b^2 = a ^ 2 + b ^ 2 + c ^ 2.] В итоге получается сумма трех квадратов, что является теоремой Пифагора для трехмерного пространства.
Любопытно, что теорему Пифагора можно обобщить даже для (n-)мерного пространства, где получится сумма (n) – квадратов.[d^2 = d^2_1 + d^2_2 + d^2_3 + cdots + d^2_n]
Теорема в реальной жизни
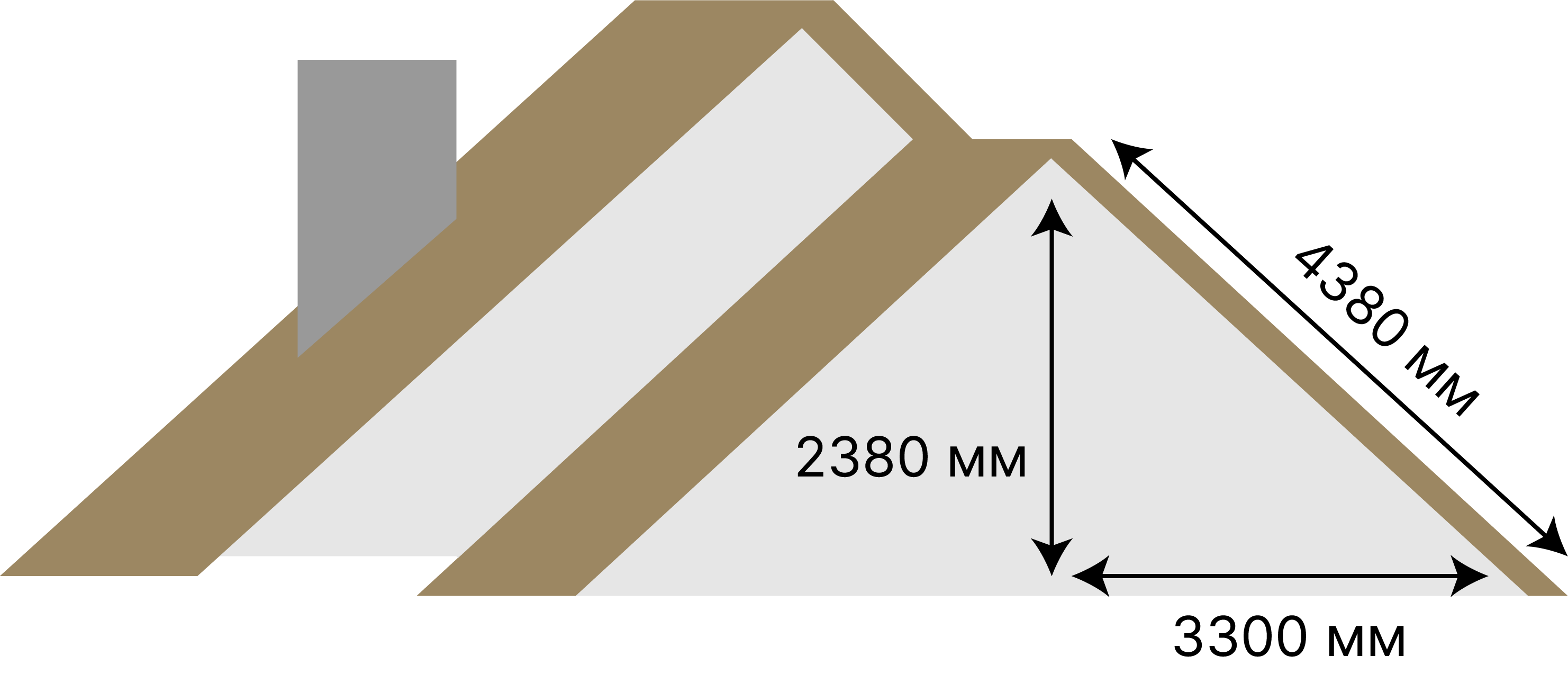
Строительство
При известных сторонах прямоугольника, теорема Пифагора позволяет найти длину диагонали. Это применение теоремы часто используется в строительстве, деревообработке или других архитектурных проектах. Рассмотрим один маленький пример: предположим, что вам надо построить двухскатную крышу на уже построенное здание (см. изображение ниже). Если вам известна высота и ширина крыши, которую нужно покрыть, вы можете использовать теорему Пифагора, чтобы найти длину крыши. Например, если высота крыши была бы (2880) миллиметров, а ширина (3300) миллиметров, то по теореме Пифагора: [c^2=a^2+b^2 =19184400 = 4380^2] Значит длина крыши должна быть (4380) миллиметров, что можно использовать для покупки необходимого количества строительных материалов.
Короткий путь
Множество приключений начинается с небезызвестной фразы “Я знаю короткий путь”. Но кто же знал, что теорема Пифагора вдруг может положить конец этим внезапным путаницам, когда короткий путь оказывается куда длиннее. Представим: чтобы попасть домой у вас есть готовый маршрут – сначала (120) метров на юг, а затем (50) метров на запад. Общее расстояние, пройденное по этому маршруту, составит (170) метров. Другой способ добраться к дому – пойти на юго-запад по третьей стороне треугольника. Если применить теорему Пифагора для вычисления расстояния, получится: [ 120^2 + 50^2 = 14400 + 2500 = 16900 = c^2 Rightarrow c = sqrt{250000} = 130.] Тогда прогулка по гипотенузе этого треугольного маршрута будет на (170-130 = 40) метров короче, чем прогулка по катетам.
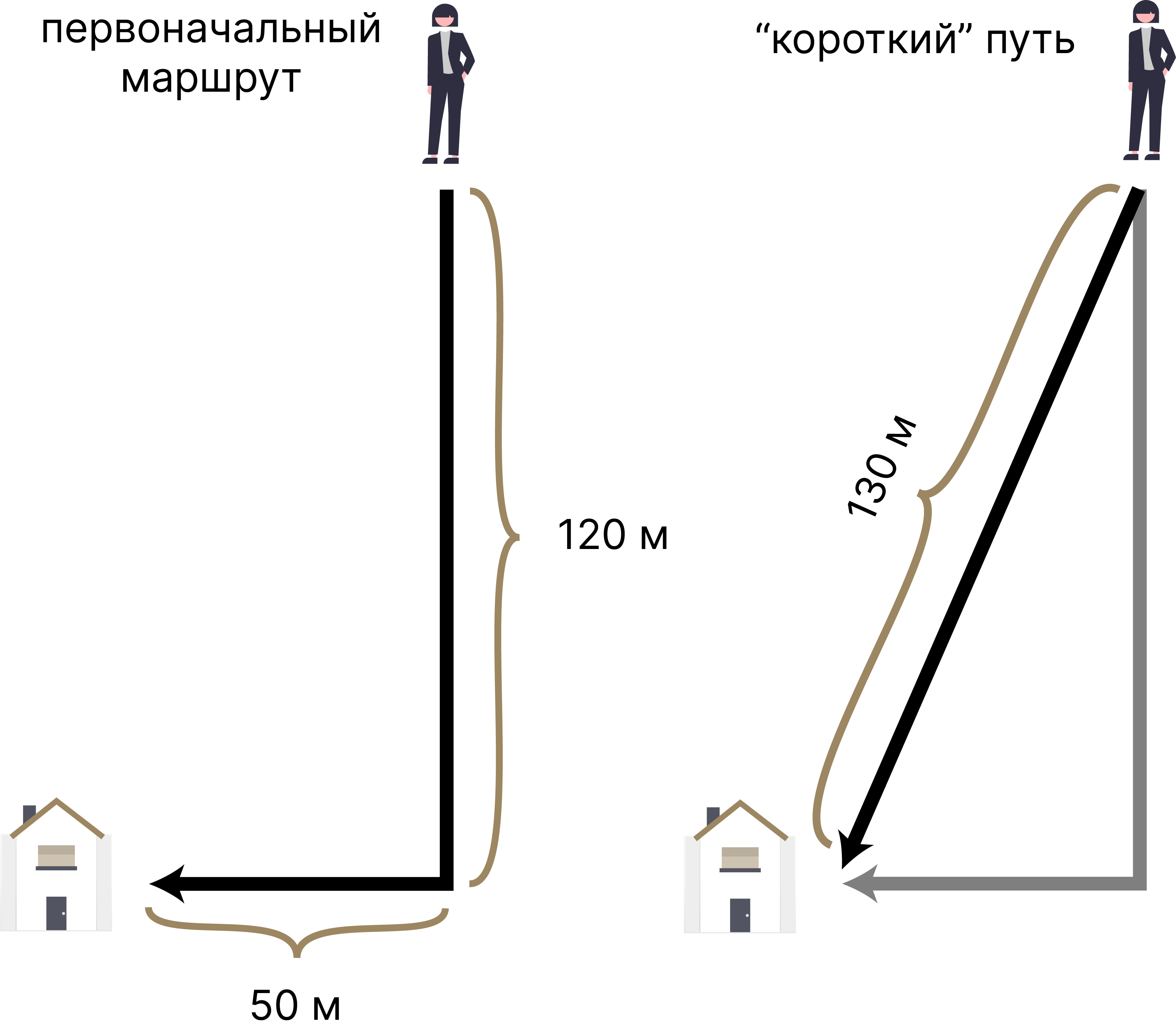
Подобные расчеты будут верны для всех треугольников (вспомните неравенство треугольника), даже не прямоугольных, однако именно в случае прямоугольных треугольников благодаря теореме Пифагора мы можем легко вычислить путь и время, которое можно сэкономить.
Социальные сети
С помощью теоремы Пифагора мы можем разделить любую гипотенузу (c^2) на два меньших катета (a^2 + b^2). В действительности «гипотенуза» может быть чем угодно: длиной, энергией, работой, отрезком времени или даже количеством людей в социальной сети.
Чтобы увидеть теорему Пифагора в социальных сетях, для начала разберемся что значит “ценность сети” для каждого индивидуального пользователя: чем больше пользователей находятся в какой-то социальной сети, тем полезнее считается сеть для каждого участника. Эта ценность прямо зависит от количества пользователей, ведь подключение нового пользователя означает возможность связаться с большим количеством людей. Роберт Меткалф, со-изобретатель сети Ethernet, сформулировал более формальный закон о математических единицах ценности сети, который затем переименовали в его честь. Закон Меткалфа гласит:
Математическая единица полезности сети пропорциональна квадрату численности пользователей этой сети.
Согласно этому закону, сеть из (50) миллионов человек равноценна сумме социальных сетей из (40) и (30) миллионов человек. Ничего не напоминает? Египетский треугольник со сторонами (3-4-5) – примитивная пифагорова тройка. Довольно удивительно: во (2)-й и (3)-й социальных сетях всего насчитывается (70) миллионов человек, но эти сети не являются единым целым. Следовательно, сеть из (50) миллионов человек оказывается столь же ценна, как две другие сети вместе взятые.
Так теорема Пифагора разбирается в запутанных социальных сетях и их ценности.
Сортируем книги
Книги в библиотеке или книжных магазинах, как правило, расставляются в алфавитном порядке. И каждый раз, когда библиотека или магазин получают новую партию книг, им необходимо отсортировать эти книги и расставить их в правильном порядке от А до Я. Существует огромное множество способов с разным числом промежуточных операций, с помощью которых можно отсортировать книги. Один из самых простых способов – просмотреть название всех книг и найти ту, что в правильном алфавитном порядке должна быть первой, а затем поставить ее первой по счету на полку. После этого найти книгу, которая должна быть второй, и поставить ее после первой книги на ту полку. Так же третью, четвертую, и наконец (n)-ую книгу. Закончив раскладывать все книги, мы получим правильный ряд, расставленный в алфавитном порядке. В итоге получится, что количество действий, сделанных при расстановке, для очень большого количества книг будет примерно пропорционально квадрату количества книг. Именно это свойство помогает нам воспользоваться теоремой Пифагора и известными примитивными тройками:[text{Время для } 50 text{ книг}= text{Время для } 40 text{ книг}+ text{Время для } 30 text{ книг}.]Примечательно, что это будет работать с любыми объектами при их сортировки. Если рассмотреть общее количество операций и воспользоваться теоремой Пифагора, то обнаружиться что-то удивительное: количество операций для (50) объектов равно количеству операций для (40) и (30) объектов вместе взятых. Иначе говоря, (70) объектов, распределенные между двумя группами, могут быть отсортированы так же быстро, как (50) объектов в одной группе. Учитывая эту взаимосвязь, мы можем эффективнее разделить элементы на отдельные группы, а затем отсортировать эти подгруппы. Действительно, именно такой подход используется в быстрой сортировке – одном из лучших методов сортировки общего назначения.
Заключение
Теорема Пифагора – это не просто формула. Теорема Пифагора – сумма квадратов катетов, равная квадрату гипотенузе, изменившая мир. Простое равенство, берущее начало со времен пифагорейской математики, выведенное то ли вавилонскими учеными, то ли действительно Пифагором, смогло создать что-то большое и великое – человеческую цивилизацию. Древний Египет и Месопотамия, строительство домов и архитектура романских и готических соборов, современные социальные сети, радары и навигаторы – все, что связано с человеком, так же связано с теоремой Пифагора. В математике же теорема Пифагора занимает особенное место, и в ее кратком равенстве открывается простор для размышлений ученых всех времен, уверенных, что настоящая математика очаровательна, красива и увлекательна, как сама теорема Пифагора.
Данной статьей мы завершаем цикл “В чем прелесть математики”. Мы надеемся, что наши публикации про изящество визуальных доказательств, вероятности и их связь с теоремой Байеса, разрезающих (2000) проводов Вовку и Азамата, а также таинственные бесконечности помогли вам взглянуть на математику под другим углом и стали очередным шагом в мире этой прелестной науки.
Фонд «Beyond Curriculum» публикует цикл материалов «В чем прелесть предмета» в партнерстве с проектом «Караван знаний» при поддержке компании «Шеврон». Караван знаний – инициатива по исследованию и обсуждению передовых образовательных практик с участием ведущих казахстанских и международных экспертов.
Редактор статьи: Дарина Мухамеджанова
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Прямоугольный треугольник. Теорема Пифагора
Прямоугольный треугольник – это треугольник, один из углов которого равен (90^circ) (прямой).
Сторона, лежащая напротив прямого угла, называется гипотенузой ((AB)), а две другие стороны — катетами ((AC) и (BC)).

(bullet) Катет, лежащий против угла (30^circ), равен половине гипотенузы.
Следовательно, если, например, (angle A=30^circ), то (BC=dfrac12AB).
(bullet) Сумма острых углов прямоугольного треугольника равна (90^circ): (angle A+angle B=90^circ).
Следовательно, если в прямоугольном треугольнике один из острых углов равен (45^circ), то такой треугольник является равнобедренным.
(bullet) Если в прямоугольном треугольнике (ABC) провести высоту (CH) из прямого угла, то (angle BAC=angle BCH) и (angle
ABC=angle
ACH):

(bullet) Теорема Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов: [AB^2=AC^2+BC^2]
(bullet) (triangle ABCsim triangle AHCsim triangle BHC)
(bullet) Высота, проведенная из вершины прямого угла, есть среднее геометрическое (среднее пропорциональное) отрезков, на которые делится гипотенуза этой высотой: [CH=sqrt{AHcdot HB}]
Задание
1
#3770
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), угол (A) равен (30^circ), (AB=2sqrt3). Найдите высоту (CH).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=sqrt3).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=sqrt3:2).
Тогда по теореме Пифагора из (triangle BCH): [CH=sqrt{BC^2-BH^2}=sqrt{dfrac94}=1,5]
Ответ: 1,5
Задание
2
#3771
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (AH), если (AB=2).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=1).
Тогда по теореме Пифагора из (triangle ABC): [AC=sqrt{AB^2-BC^2}=sqrt3] Из прямоугольного (triangle AHC): (HC=0,5AC=sqrt3:2). Тогда по теореме Пифагора [AH=sqrt{AC^2-HC^2}=1,5]
Ответ: 1,5
Задание
3
#3772
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C) равен (90^circ), (CH) – высота, угол (A) равен (30^circ). Найдите (BH), если (AB=4).

Так как катет, лежащий против угла (30^circ), равен половине гипотенузы, то (BC=0,5AB=2).
По свойству прямоугольного треугольника (angle BCH=angle
A=30^circ), следовательно, из (triangle BCH): (HB=0,5
BC=1).
Ответ: 1
Задание
4
#3773
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) ( AB=BC=AC=2sqrt3). Найдите высоту (CH).
Так как (AC=BC), то (CH) также является медианой, следовательно, (AH=0,5 AB=sqrt3). Тогда по теореме Пифагора из (triangle ACH): [CH=sqrt{AC^2-AH^2}=3]
Ответ: 3
Задание
5
#3774
Уровень задания: Равен ЕГЭ
В равностороннем треугольнике (ABC) высота (CH) равна (2sqrt3). Найдите (AB).

Так как (AC=BC), то (CH) также является медианой. Следовательно, если (AH=a), то (AB=AC=2a). Тогда по теореме Пифагора из (triangle
ACH): [AC^2=AH^2+CH^2quadRightarrowquad 4a^2=a^2+12quadRightarrowquad
a=2quadRightarrowquad AB=2a=4]
Ответ: 4
Задание
6
#3775
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC=4), (angle C=30^circ). Найдите высоту (AH).

Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (AH=0,5AC=2).
Заметим, что условие (BC=4) в данной задаче является лишним.
Ответ: 2
Задание
7
#3776
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) (AC=BC), высота (AH) равна (4), угол (C) равен (30^circ). Найдите (BC).

Рассмотрим прямоугольный (triangle ACH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (4=AH=0,5AC), откуда (8=AC=BC).
Ответ: 8

УСТАЛ? Просто отдохни
