Углы 




Рис. 149
Если вектор а имеет длину, равную единице масштаба, т. е. если 

Из формул (1), (2), (3) следует:

Пример. Найти углы, образуемые осями координат с вектором 
Решение, 

Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно – 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = – 9 3 · 6 = – 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( – 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = – 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , – 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 2 2 + 0 2 + ( – 1 ) 2 · 1 2 + 2 2 + 3 2 = – 1 70 ⇒ a → , b → ^ = a r c cos ( – 1 70 ) = – a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( – 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( – 1 ) · 3 = – 1 cos a → , b → ^ = a → , b → ^ a → · b → = – 1 5 · 14 = – 1 70 ⇒ a → , b → ^ = – a r c cos 1 70
Ответ: a → , b → ^ = – a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , – 1 ) , B ( 3 , 2 ) , C ( 7 , – 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 – 2 , – 2 – ( – 1 ) ) = ( 5 , – 1 ) B C → = ( 7 – 3 , – 2 – 2 ) = ( 4 , – 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( – 1 ) · ( – 4 ) 5 2 + ( – 1 ) 2 · 4 2 + ( – 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 – 2 · O A · O B · cos ( ∠ A O B ) ,
b → – a → 2 = a → + b → – 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 – b → – a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Проекция вектора на ось
Вектор может отбрасывать тень (проекцию) на какую-нибудь ось
Если:
- вектор параллелен оси, то «его проекция = его длина», пример для вектора ( vec );
- вектор перпендикулярен оси, то его проекция равна нулю, пример для вектора ( vec );
- проекция направлена против оси, то её записывают со знаком «-», пример для вектора ( vec ).
- чем больше вектор наклоняется к оси, тем больше его проекция на эту ось. Сравните проекции векторов ( vec ) и ( vec ).
Примечание:
Длина вектора – это положительная величина, а проекция вектора может быть отрицательной
Как разложить вектор на проекции
Мы уже находили длину и направление вектора по его координатам.
Теперь решим обратную задачу: пользуясь длиной и направлением вектора, найдем его координаты.
На плоскости (две оси) легко разложить вектор на проекции, если известны:
- длина вектора и
- угол между вектором и какой-либо осью (угол обозначается дугой).
Алгоритм действий для разложения вектора на проекции
- Проводим прямоугольник так, чтобы вектор стал его диагональю.
- Диагональ разделит прямоугольник на треугольники. Эти два треугольника прямоугольные.
- Выберем треугольник, в котором угол отмечен дугой.
- Дуга одним своим концом всегда касается гипотенузы, а вторым концом – одного из катетов.
Важно! Вектор, который мы раскладываем, всегда является гипотенузой.
Формулы разложения вектора на проекции
Формулы разложения легко запомнить с помощью фразы:
Гипотенузу умножаем на косинус (угла), получаем катет, который касается (дуги).
На языке математики эта фраза запишется так:
[ |vec| cdot cos(alpha) = m_ ]
Катет ( m_ ) – это «x» координата вектора.
Если длину вектора умножим на синус, то получим второй катет:
[ |vec| cdot sin(alpha) = m_ ]
Катет ( m_ ) – это «y» координата вектора.
Обе формулы запишем в виде системы:
[ large boxed <beginleft|vecright| cdot cos(alpha) = m_ \ left|vecright| cdot sin(alpha) = m_ end> ]
Величина ( |vec| ) — это длина вектора ( vec )
Как найти угол между вектором и осью координат
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).
Проекция вектора на ось обозначается через al или , а угол между осью и вектором будем обозначать так: . Таким образом,
(2)
Если – углы, образованные вектором с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора на координатные оси будут равны
(3)
В дальнейшем предполагается, что система координат – прямоугольная.
Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле
(4)
т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.
Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).
[spoiler title=”источники:”]
http://www.pm298.ru/reshenie/vektor4.php
[/spoiler]
ТЕМА 7.4 УГОЛ МЕЖДУ ВЕКТОРАМИ. УГОЛ МЕЖДУ
ВЕКТОРОМ И ОСЬЮ
Содержание учебного материала:
Применение векторов для вычисления величин
углов и расстояний:
1.Понятие угла между векторами.
2.Формула вычисления угла между векторами.
3.Понятие направляющих косинусов вектора.
4.Формулы вычисления направляющих косинусов
вектора.
1.Понятие угла
между векторами.
Угол между векторами –
это угол между их направлениями (рис.1).
Угол между
сонаправленными векторами равен 0.
Угол между
противоположно направленными векторами равен
Угол между
ортогональными векторами равен.
2. Формула вычисления угла между векторами.
Из определения
скалярного произведения векторов находим угол
между векторами:
=
;
=
.
Пример 1. Найдите угол АСВ в треугольнике АВС, если, В(-2;0;7) и
С(-3;-2;5).
Решение. 1. Угол АСВ в треугольнике АВС находится между векторами
и Определим координаты векторов:
.
2. Найдём угол между векторами и
по формуле (1), подставив в неё
соответствующие координаты:

3. Определим величину искомого угла по таблице значений тригонометрических
функций или с помощью калькулятора:
Итак, угол между
векторами и
найден:
.


вектора.
Определим углы, составляемые вектором AB = (x; y; z) с
координатными осями:
с осью ОХ :
с осью ОY :
с осью ОZ :
Пример 2.
Найти углы, составляемые
вектором с координатными осями, если
Решение.
1. Найдём координаты вектора:
2.Вычислим длину вектора:
3. Определим углы, составляемые вектором с координатными осями:
с осью ОХ :
с осью ОY :
с осью ОZ :
Итак, углы, составляемые вектором с координатными осями, равны
,
,
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a→ и b→ , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы OA→=b→ и OB→=b→
Углом между векторами a→ и b→ называется угол между лучами ОА и ОВ.
Полученный угол будем обозначать следующим образом: a→,b→^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a→,b→^=0, когда векторы являются сонаправленными и a→,b→^=π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π2 радиан.
Если хотя бы один из векторов является нулевым, то угол a→,b→^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a→, b→=a→·b→·cosa→,b→^.
Если заданные векторы a→ и b→ ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cosa→,b→^=a→,b→a→·b→
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a→ и b→ . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно -9. Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cosa→,b→^=-93·6=-12 ,
Теперь определим угол между векторами: a→,b→^=arccos (-12)=3π4
Ответ: cosa→,b→^=-12, a→,b→^=3π4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a→=(ax, ay), b→=(bx, by) выглядит так:
cosa→,b→^=ax·bx+ay·byax2+ay2·bx2+by2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a→=(ax, ay, az), b→=(bx, by, bz) будет иметь вид: cosa→,b→^=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2
Исходные данные: векторы a→=(2, 0, -1), b→=(1, 2, 3) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cosa→,b→^=2·1+0·2+(-1)·322+02+(-1)2·12+22+32=-170⇒a→,b→^=arccos(-170)=-arccos170
- Также можно определить угол по формуле:
cosa→,b→^=(a→, b→)a→·b→,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a→=22+02+(-1)2=5b→=12+22+32=14a→,b→^=2·1+0·2+(-1)·3=-1cosa→,b→^=a→,b→^a→·b→=-15·14=-170⇒a→,b→^=-arccos170
Ответ: a→,b→^=-arccos170
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A(2, -1), B(3, 2), C(7, -2). Необходимо определить косинус угла между векторами AC→ и BC→.
Решение
Найдем координаты векторов по координатам заданных точек AC→=(7-2, -2-(-1))=(5, -1)BC→=(7-3, -2-2)=(4, -4)
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cosAC→, BC→^=(AC→, BC→)AC→·BC→=5·4+(-1)·(-4)52+(-1)2·42+(-4)2=2426·32=313
Ответ: cosAC→, BC→^=313
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы OA→=a→ и OB→=b→ , тогда, согласно теореме косинусов в треугольнике ОАВ, будет верным равенство:
AB2=OA2+OB2-2·OA·OB·cos(∠AOB) ,
что равносильно:
b→-a→2=a→+b→-2·a→·b→·cos(a→, b→)^
и отсюда выведем формулу косинуса угла:
cos(a→, b→)^=12·a→2+b→2-b→-a→2a→·b→
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
cos(a→, b→)^=a→, b→a→·b→
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Содержание:
- Координаты вектора
- Длина (модуль) вектора
- Угол между векторами
- Разложение вектора по ортам координатных осей
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
Вектора применяются во многих науках, таких как: математика, физика, геометрия и многих других
прикладных науках. На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию векторов и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по векторам, прочитать
все определения и свойства. Список тем находится в правом меню.
Координаты вектора
Теоретический материал по теме – координаты вектора.
Пример
Запись $overline{a}=(5 ;-2)$ означает, что вектор $overline{a}$
имеет следующие координаты: абсцисса равна 5, ордината равна -2.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Заданы векторы $overline{a}=(-3 ; 5)$
и $overline{b}=(0 ;-1)$. Найти координаты вектора $overline{c}=overline{a}+overline{b}$
Решение. $overline{c}=overline{a}+overline{b}=(-3 ; 5)+(0 ;-1)=(-3+0 ; 5+(-1))=(-3 ; 4)$
Пример
Задание. Вектор $overline{a}=(3 ;-2)$.
Найти координаты вектора 2$overline{a}$
Решение. $2 overline{a}=2 cdot(3 ;-2)=(2 cdot 3 ; 2 cdot(-2))=(6 ;-4)$
Пример
Задание. Найти координаты вектора $overline{A B}$,
если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline{A B}=(1-(-4) ;-3-2)=(5 ;-5)$
Длина (модуль) вектора
Теоретический материал по теме – длина вектора.
Пример
Задание. Найти длину вектора $overline{a}=(-4 ; 3)$
Решение. Используя формулу, получаем:
$|overline{a}|=sqrt{(-4)^{2}+3^{2}}=sqrt{16+9}=sqrt{25}=5$
Пример
Задание. Найти длину вектора $overline{a}=(1 ; 0 ;-4)$
Решение. Используя формулу, получаем:
$|overline{a}|=sqrt{1^{2}+0^{2}+(-4)^{2}}=sqrt{1+0+16}=sqrt{17}$
Угол между векторами
Теоретический материал по теме – угол между векторами.
Пример
Задание. Известно, что скалярное произведение двух векторов $(overline{a} ; overline{b})=2$,
а их длины $|overline{a}|=2,|overline{b}|=2$.
Найти угол между векторами $overline{a}$ и
$overline{b}$.
Решение. Косинус искомого угла:
$$cos (bar{a}, bar{b})=frac{(bar{a} ; bar{b})}{|bar{a}| cdot|bar{b}|}=frac{2}{2 cdot 2}=frac{1}{2} Rightarrow(bar{a}, bar{b})=60^{circ}$$
Пример
Задание. Найти угол между векторами $overline{a}=(1 ; sqrt{3})$ и
$overline{b}=(1 ; 0)$
Решение. Косинус искомого угла
$$cos (bar{a}, bar{b})=frac{1 cdot 1+sqrt{3} cdot 0}{sqrt{1^{2}+(sqrt{3})^{2}} cdot sqrt{1^{2}+0^{2}}}=frac{1}{2}$$
$$(bar{a}, bar{b})=arccos frac{1}{2}=60^{circ}$$
Пример
Задание. Найти угол между векторами $overline{a}=(1 ; 3)$
и $overline{b}=(2 ; 1)$
Решение. Косинус искомого угла:
$$cos (bar{a}, bar{b})=frac{1 cdot 2+3 cdot 1}{sqrt{1^{2}+3^{2}} cdot sqrt{2^{2}+1^{2}}}=frac{5}{sqrt{10} cdot sqrt{5}}=sqrt{frac{1}{2}}=frac{sqrt{2}}{2}$$
$$(bar{a}, bar{b})=arccos frac{sqrt{2}}{2}=45^{circ}$$
Разложение вектора по ортам координатных осей
Теоретический материал по теме – разложение вектора по ортам.
Пример
Задание. Зная разложения вектора $overline{a}$
по базисной системе векторов: $overline{a}=3 overline{i}-overline{k}$, записать координаты этого вектора в пространстве.
Решение. Коэффициенты при ортах и есть координатами вектора, поэтому из того, что $overline{a}=3 overline{i}-0 cdot overline{j}-overline{k}$,
получаем, что $overline{a}=(3 ; 0 ;-1)$
Пример
Задание. Вектор $overline{a}$ задан
своими координатами: $overline{a}=(2 ;-1 ; 5)$. Записать разложение данного вектора по ортам осей координат.
Решение. Координаты вектора – это коэффициенты при ортах координатных осей в разложении вектора
по базисной системе векторов, поэтому искомое разложение:
$overline{a}=2 overline{i}-overline{j}+5 overline{k}$
Скалярное произведение векторов
Теоретический материал по теме – скалярное произведение векторов.
Пример
Задание. Вычислить скалярное произведение векторов $overline{a}$ и
$overline{b}$ , если их длины соответственно равны 2 и 3,
а угол между ними 60°.
Решение. Так как из условия $|overline{a}|=2$,
$|overline{b}|=3$, а 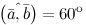
$overline{a} cdot overline{b}=(overline{a}, overline{b})=2 cdot 3 cdot cos 60^{circ}=6 cdot frac{1}{2}=3$
Пример
Задание. Найти скалярное произведение векторов $overline{a}=(3 ;-1)$ и
$overline{b}=(-2 ; 7)$
Решение. Скалярное произведение
$overline{a} overline{b}=3 cdot(-2)+(-1) cdot 7=-6-7=-13$
Векторное произведение векторов
Теоретический материал по теме – векторное произведение векторов.
Пример
Задание. Найти векторное произведение векторов $overline{a}=(6 ; 7 ; 10)$ и
$overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$overline{a} times overline{b}=left| begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {6} & {7} & {10} \ {8} & {5} & {9}end{array}right|=overline{i} left| begin{array}{cc}{7} & {10} \ {5} & {9}end{array}right|-overline{j} left| begin{array}{cc}{6} & {10} \ {8} & {9}end{array}right|+overline{k} left| begin{array}{cc}{6} & {7} \ {8} & {5}end{array}right|=$
$=overline{i}(7 cdot 9-5 cdot 10)-overline{j}(6 cdot 9-8 cdot 10)+overline{k}(6 cdot 5-8 cdot 7)=$
$=13 overline{i}+26 overline{j}-26 overline{k}=(13 ; 26 ;-26)$
Смешанное произведение векторов
Теоретический материал по теме – смешанное произведение векторов.
Пример
Задание. Вычислить объем пирамиды, построенной на векторах $overline{a}=(2 ; 3 ; 5)$,
$overline{b}=(1 ; 4 ; 4)$,
$overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $overline{a}$,
$overline{b}$ и $overline{c}$:
$(overline{a}, overline{b}, overline{c})=left| begin{array}{lll}{2} & {3} & {5} \ {1} & {4} & {4} \ {3} & {5} & {7}end{array}right|=2 cdot 4 cdot 7+1 cdot 5 cdot 5+3 cdot 4 cdot 3-$
$-3 cdot 4 cdot 5-5 cdot 4 cdot 2-1 cdot 3 cdot 7=-4$
$$V_{пир}=frac{1}{6}|(overline{a}, overline{b}, overline{c})|=frac{1}{6} cdot 4=frac{2}{3}$$
Читать первую тему – операции над векторами,
раздела векторы.





