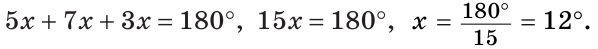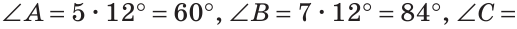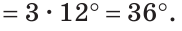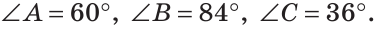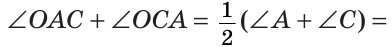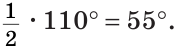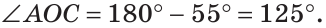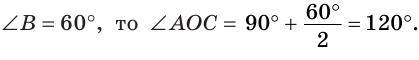Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Как найти угол abc треугольника
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
Сумма углов треугольника – определение и вычисление с доказательствами и примерами решения
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
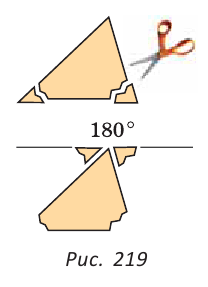
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
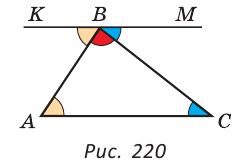
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 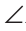
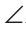
Доказательство:
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 





Следствия.
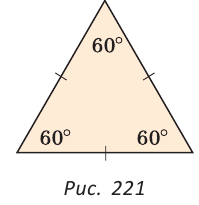
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
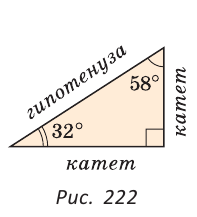
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
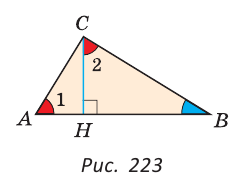
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
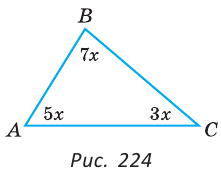
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 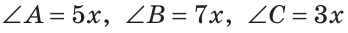
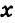
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
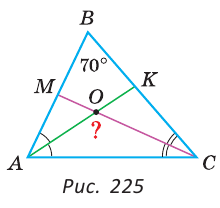
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Сумма углов А и С треугольника ABC равна 180° – 70° = 110°. Так как биссектриса делит угол пополам, то
Из треугольника АОС находим:
Замечание. Если 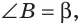
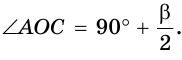
Пример:
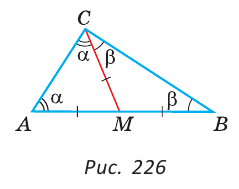
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 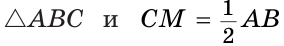
Докажем, что























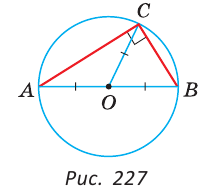
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
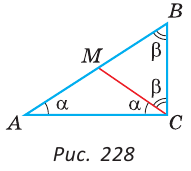
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Внешний угол треугольника
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
[spoiler title=”источники:”]
http://oge.sdamgia.ru/search?search=%D0%9D%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D1%83%D0%B3%D0%BE%D0%BB%20ABC
http://www.evkova.org/summa-uglov-treugolnika
[/spoiler]
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
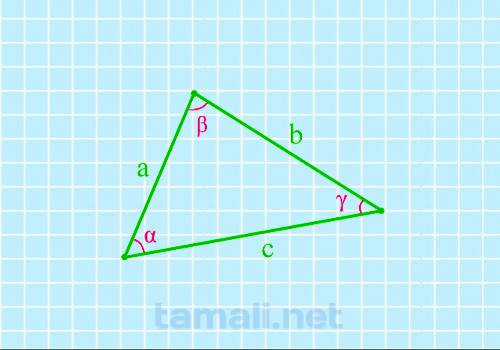
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
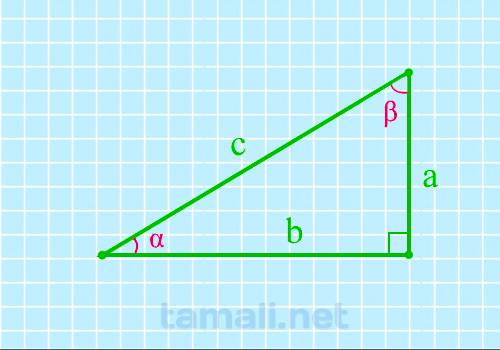
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
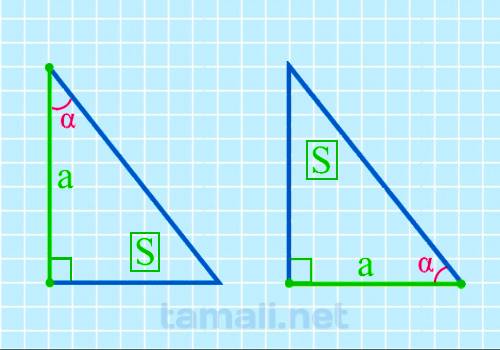
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
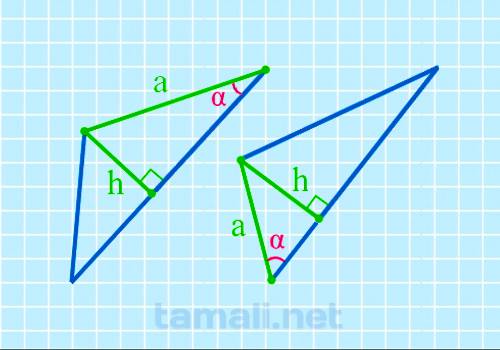
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
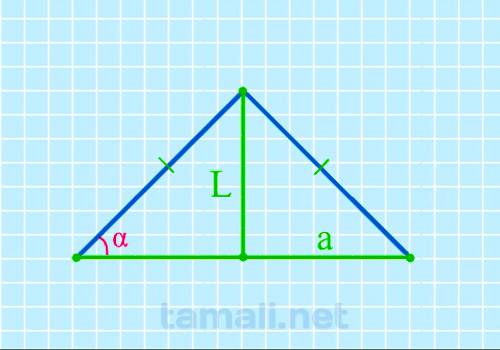
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
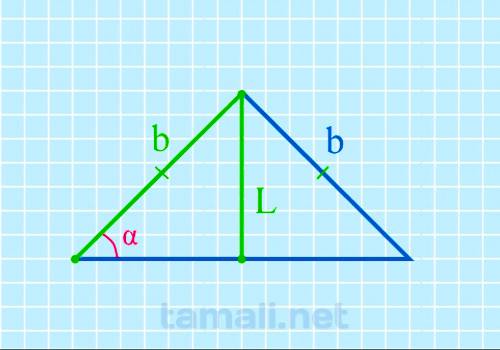
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
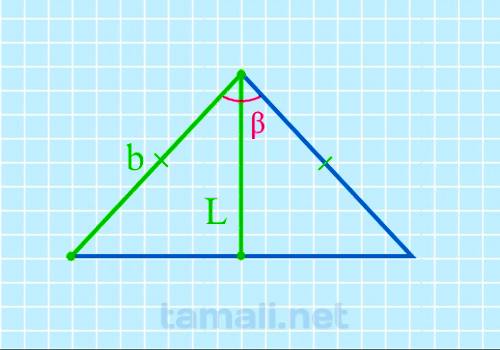
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
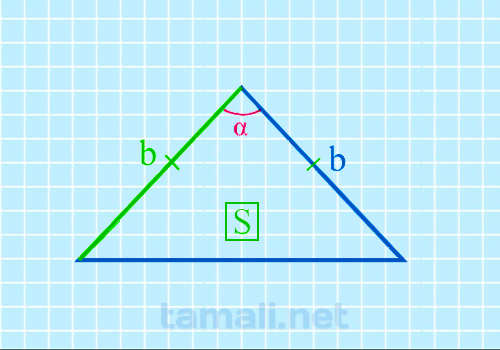
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
eigenbasis
Гуру
(3250)
1 год назад
1. находим вектора, образующие угол (BA и BC):
BA = A – B = (-1, 1)
BC = C – B = (-1, -1)
2. находим скалярное произведение этих векторов
⟨BA, BC⟩ = (-1)*(-1) + 1*(-1) = 0
3. находим длины этих векторов (конкретно здесь уже ясно, что угол 90 градусов, но для других координат точек этот шаг надо было бы сделать)
|BA| = √((-1)² + (1)²) = √2
|BC| = √((-1)² + (-1)²) = √2
4. косинус угла между векторами равен их скалярному произведению, делённому на произведение длин этих векторов, то есть
cos(ABC) = ⟨BA, BC⟩ / (|BA| * |BC|) = 0 / 2 = 0
Поэтому угол ABC = 90 градусов
Альтернативный способ (если вы знаете, что такое определитель матрицы 2х2).
1. опять находим координаты образующих векторов
BA = (-1, 1) и BC = (-1, -1)
2. составляем из них матрицу и находим её определитель
| -1 -1 |
| 1 -1 | = (-1)*(-1) – (-1)*1 = 2
из геометрического смысла определителя он равен удвоенной площади треугольника, то есть 2*S(ABC) = 2
3. делим определитель на произведение длин векторов и из формулы площади треугольника через синус получаем синус нашего угла
sin(ABC) = 2 / (√2 * √2) = 2 / 2 = 1
отсюда аналогично заключаем, что угол 90 градусов
eigenbasisГуру (3250)
1 год назад
Из ответа ниже правда стоило бы считать не определитель, а его модуль (ориентация площади нам правда здесь не очень инетесна)
Тадасана
Просветленный
(32140)
1 год назад
Применяем оба способа 1 и 2
Площадь параллелограмма-то ориентированная, это ж симплектическое скалярное пргизведение, согласованное с евклидовым скалярыным произведением в E2, оно называется псевдокакое-то.
Зная синус и косинус угла, найдем и угол с т. до 2пи, если считать, что он гткладывается против часовй
Формулы треугольника ABC зная 1 сторону и 2 угла
- Найдем угол B
- Найдем сторону AB
- Найдем сторону BC
- Найдем периметр P треугольника ABC
- Найдем площадь S треугольника ABC
- Найдем высоту H проведенную к стороне AC
Так как мы знаем значение угла A и угла С, а сумма всех углов всегда равна 180 градусов, то
(angle B=180-angle А- angleС=180-htmlClass{kA}{50}-htmlClass{kC}{50}=htmlClass{kB}{80}degree)
Что бы найти сторону AB, необходимо знать длину стороны AC, а также углы С и B
(AB = {AC * sin(angle C)over sin(angle B)} ={htmlClass{kAC}{8} * sin( htmlClass{kC}{50})over sin( htmlClass{kB}{80})}=htmlClass{kAB}{6.223})
Для нахождения стороны BC необходимо знать длину стороны AC, угол A и угол B
(BC = {AC * sin(angle A)over sin(angle B)} ={htmlClass{kAC}{8} * sin( htmlClass{kA}{50})over sin( htmlClass{kB}{80})}=htmlClass{kBC}{6.223})
Периметр треугольника равен сумме длин всех его сторон
(P=AB+BC+AC=htmlClass{kAB}{6.223}+htmlClass{kBC}{6.223}+htmlClass{kAC}{8}=htmlClass{kP}{20.446})
Зная периметр и длины всех сторон, рассчитаем площадь треугольника
(S=htmlClass{fontm}{ sqrt{{Pover 2}*({Pover 2}-AC)*({Pover 2}-BC)*({Pover 2}-AB)}}=htmlClass{fontm}{ sqrt{{htmlClass{kP}{20.446}over 2}*({htmlClass{kP}{20.446}over 2}-htmlClass{kAC}{8})*({htmlClass{kP}{20.446}over 2}-htmlClass{kBC}{6.223})*({htmlClass{kP}{20.446}over 2}-htmlClass{kAB}{6.223})}}=htmlClass{kS}{19.068})
Для нахождения высоты треугольника, понадобится его площадь и длина стороны AC
(H={2 * Sover AC}={2 * htmlClass{kS}{19.068}over htmlClass{kAC}{8}}=htmlClass{kH}{4.767})
Примеры решения треугольника ABC зная 1 сторону и 2 угла
( Дано: triangle ABC;)
( AC=htmlClass{kAC}{8} см;)
( angle A=htmlClass{kA}{50} degree;)
( angle C=htmlClass{kC}{50} degree;)
( Найти: P _{triangle ABC} ?)
( Решение:)
(P=AB+BC+AC)
(angle B=180-angle А- angleС=180-htmlClass{kA}{50}-htmlClass{kC}{50}=htmlClass{kB}{80}degree)
(AB = {AC * sin(angle C)over sin(angle B)} ={htmlClass{kAC}{8} * sin( htmlClass{kC}{50})over sin( htmlClass{kB}{80})}=htmlClass{kAB}{6.223}см)
(BC = {AC * sin(angle A)over sin(angle B)} ={htmlClass{kAC}{8} * sin( htmlClass{kA}{50})over sin( htmlClass{kB}{80})}=htmlClass{kBC}{6.223}см)
(P=htmlClass{kAB}{6.223}см+htmlClass{kBC}{6.223}см+htmlClass{kAC}{8}см=htmlClass{kP}{20.446}см)
( Ответ:htmlClass{kP}{20.446}см)
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
Решение:
Из теоремы косинусов имеем:
Откуда
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
Используя онлайн калькулятор для arcsin и arccos находим углы A и B:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Решение:
Найдем сторону c используя теорему косинусов:
Далее, из формулы
найдем cosA:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
Вычисления выше легко производить инженерным онлайн калькулятором.
Из формулы (3) найдем cosA:
Используя онлайн калькулятор для arcsin и arccos или инженерный онлайн калькулятор находим угол A:
Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Решение:
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Откуда
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Ответ: