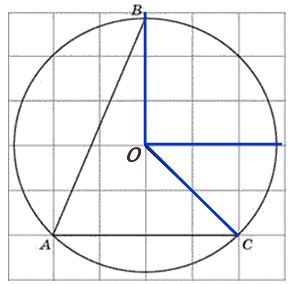
Найдите величину угла ABC. Ответ дайте в градусах
27887. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 0 . Это видно по тому как проходят АО и ОС относительно клетчатой сетки. Угол АВС это вписанный угол, построенный на той же дуге.
По свойству вписанного угла:
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности. Обозначим его точкой О, построим центральный угол АОС и вписанный угол ADC:
Центральный угол АОС равен 90 0 . По свойству вписанного угла
Известно, что у четырёхугольника вписанного в окружность сумма противоположных углов равна 180 градусам, следовательно:
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Отметим центр окружности (видно о клетчатой сетке). Обозначим его точкой О, построим центральный угол АОС:
Угол АОС равен 90 градусов. Угол АВС это вписанный угол, построенный на той же дуге. По свойству вписанного угла:
Как найти угол авс в окружности на клетчатой бумаге
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
На клетчатой бумаге изображён вписанный угол
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
[spoiler title=”источники:”]
http://oge.sdamgia.ru/search?search=%D0%9D%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D1%83%D0%B3%D0%BE%D0%BB%20ABC
http://matematikalegko.ru/okrugnost/vpisannyj-ugol-na-liste-v-kletku.html
[/spoiler]
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 529 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Тип 25 № 52
i
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4. Найдите AB.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен Найдите радиус вписанной окружности треугольника ABC.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Источники:
Банк заданий ФИПИ.
Основания трапеции равны 18 и 12, одна из боковых сторон равна а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Основания трапеции равны 18 и 10, одна из боковых сторон равна а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
В равнобедренном треугольнике боковая сторона равна 10, основание —
а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
Найдите градусную меру ∠ACB, если известно, что BC является диаметром окружности, а градусная мера центрального ∠AOC равна 96°.
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
В треугольнике ABC угол C равен 90°,
Найдите AB.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
В треугольнике ABC угол C равен 90°,
Найдите AB.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Источник: ГИА-2013. Математика. Экзамен. Вариант 1
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.
Источник: ГИА-2013. Математика. Экзамен. Вариант 2
В треугольнике ABC угол C прямой,
Найдите AB.
Источник: ГИА-2013. Математика. Экзамен. Вариант 9
В треугольнике ABC угол C прямой,
Найдите AB.
Источник: ГИА-2013. Математика. Экзамен. Вариант 10
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Источник: ГИА-2012. Математика. Диагностическая работа № 2(1вар)
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Источник: ГИА-2012. Математика. Диагностическая работа №2(2вар)
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Источник: ГИА-2013. Математика. Диагностическая работа № 1. (вар. 1) 02.10.2012г.
Всего: 529 1–20 | 21–40 | 41–60 | 61–80 …
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
А этот?
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
А такой?
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 900 + 450 = 1350 (ОС проходит по диагонали клеток).
Ответ: 135
27887. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Посмотреть решение
Небольшой итог!
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
|
Угол АВС вписан. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается. Из рисунка видно что он опирается на дугу с угловой величиной : 180+45=225° Величина угла АВС равна: 225,5:2=112,5° автор вопроса выбрал этот ответ лучшим Simple Ein 2 года назад Укажем центр окружности в точке О. Проведем отрезки АО и СО. Из графического построения видно, что малая дуга АС равна 90+45=135 градусов. Большая дуга АС будет равна 360-135=225 градусов. Угол АВС опирается на большую дугу в 225 градусов. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается. Следовательно, 225/2=112,5 градусов. Знаете ответ? |
Задачи по определению углов, вписанных в окружность, где никаких данных нет, кроме того рисунка, на котором изображены эти угла.
Данный случай нарисованного на чертеже угла несколько сложнее. Для рассмотрения и нахождения величины угла АВС, приведём дополнительные построения, которые могут помочь.
Наглядный и понятный чертёж 3 поможет легко найти значение угла.
Разбиваем искомый угол АВС на два угла:
<АВС = <СВД + <АВД , а эти два угла можно найти , используя клеточки листа, но с применением центральных углов.
<АВД = 1/2 * (<АОД) = 1/2 * 90 = 45. .
<СВД = 1/2 * (<СОД) = 1/2 * 45 .
<СОД вычисляем по чертежу (3), рассмотрев равнобедренный прямоугольный треугольник СОД1, откуда видно, что <СОД = 45.
Вот так можно просто решить сложные на первый взгляд задачи по геометрии просто по рисунку.
Спасибо за просмотр и комментарии.