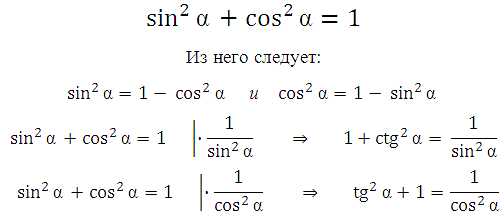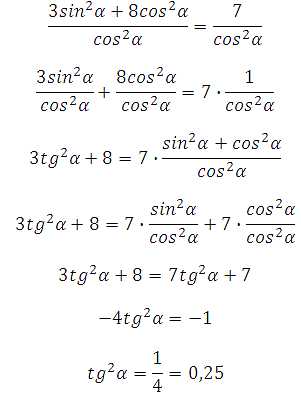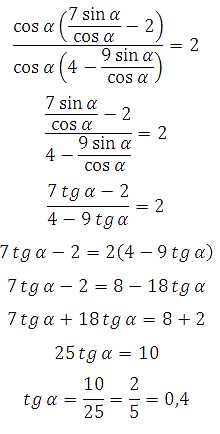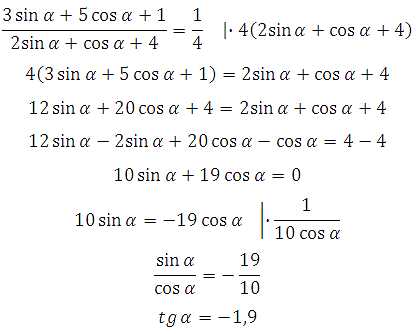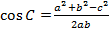Как найти угол альфа если известна площадь

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Как найти альфа окружности

Угол альфа и угол бета. Расшифровка

Популярные материалы

За сегодня:

Угол альфа и угол бета. Расшифровка

Положение суставов и головки бедренной кости оценивается не только визуально. Для определения их состояния используется специальное измерение углов по таблице Графа. Есть угол Альфа и угол Бета.

• Альфа обозначает развитие костной части ветлужной ямки.
• Бета описывает хрящевое пространство внутри ветлужной впадины.

Для здоровых детей считается нормальным, если угол Альфа составляет более 60 градусов, а угол Бета — менее 55 градусов.

Небольшое превышение нормы в 55 градусов допустимо, такой сустав считается нормальным, зрелым. Но если угол Бета составит 77 градусов, врач поставит в заключении подозрение на вывих или подвывих. Также на патологию указывает угол Альфа, который находится в диапазоне от 43 градусов.

Норма углов в таблице выглядит следующим образом.

Более 60 градусов

В пределах 55 градусов

Зрелый здоровый сустав

Менее 55 градусов, плотно облегает головку бедра

Физиологически незрелый сустав

Менее 55 градусов

Круглый, почти плоский

Менее 77 градусов

Более 77 градусов

Уплощенный или плоский

Менее 43 градусов

Не охватывает головку

Децентрация, полная незрелость сустава

В ходе роста ребенка показатели могут меняться, именно это будет учитывать доктор во время проведения УЗИ. Если ребенку уже исполнилось четыре месяца, наиболее правильным и точным методом обследования станет рентгеновский снимок.

В случае обнаружения проблем врачи стараются обследовать одновременно и костное строение малого таза. Довольно часто патология тазобедренного сустава отражается именно на нем.

В заключении доктор может быть немногословен и предпочтет ограничиться буквенно-числовым обозначением типа сустава, обнаруженного у ребенка. Запомните, что здоровый сустав всегда обозначается как 1А или 1В.

Если в заключении указано, что обнаружен сустав 2А или 2В, это означает, что у ребенка есть признаки физиологической незрелости, которая пройдет самостоятельно с огромной вероятностью, но все-таки потребует наблюдения у детского ортопеда.

Сустав 2С — сустав с признаками предвывиха. Обязательно требуется наблюдение у врача и выполнение всех его рекомендаций. 3А и 3В — суставы с подвывихом. Самая тяжелая патология — сустав 4 типа. Именно так обозначается тазобедренный сустав с признаками вывиха (дисплазии).

Угол альфа в физике. Что такое угол альфа?

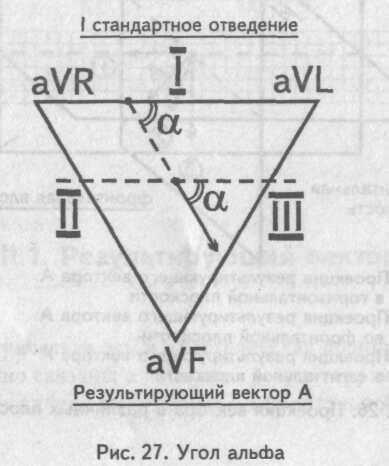
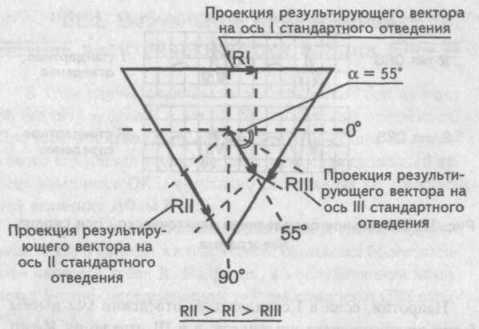
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. У г о л , образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа .

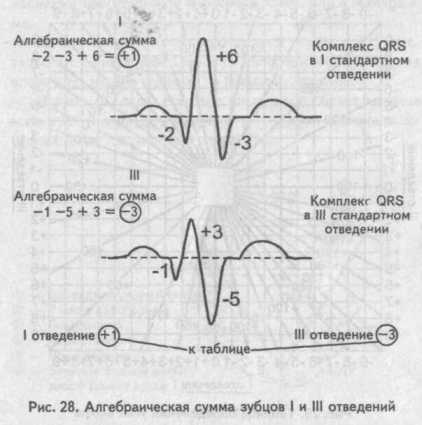
Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях.

Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (-), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

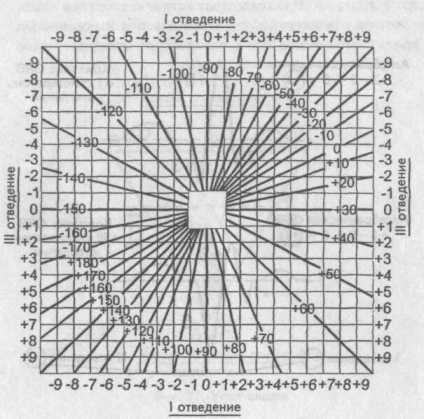
Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°.

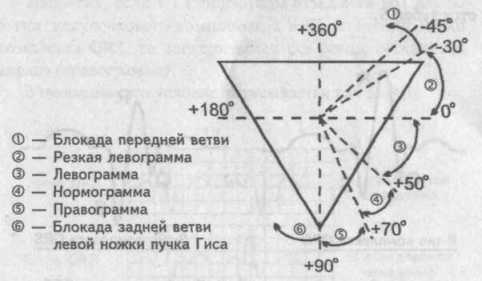
Если угол альфа находится в пределах 50-70° , говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70-90° . В обиходе такое положение электрической оси сердца называют правограммой .

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса .
Определяя угол альфа в пределах 50-0° говорят об отклонении электрической оси сердца влево, или о левограмме .
Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме .
И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса .

Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.
Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

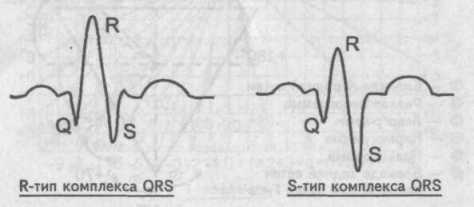
В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса заменяют понятием «определяющий зубец» комплекса QRS, визуально сопоставляя по абсолютной величине зубцы R и S. Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

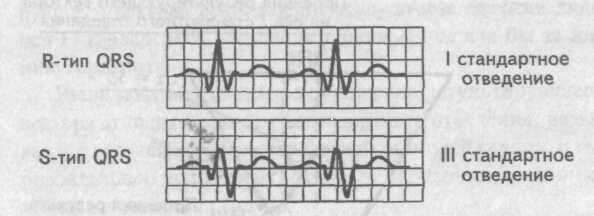
Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма) . Схематично это условие записывается как RI-SIII.

Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма) .
Упрощенно это условие записывается как SI-RIII.

Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так , что его направление совпадает с направлением оси II стандартного отведения.

На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец R в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.

Угол альфа символ. Угол атаки

Датчики углов атаки у ракеты «воздух-воздух»

Для самолёта в горизонтальном прямолинейном полёте увеличение скорости и угла атаки приводит к увеличению подъёмной силы , создаваемой крылом. В то же время увеличение угла атаки сопровождается ростом.

Торпедоносец/пикирующий бомбардировщик Supermarine Type 322 , истребитель палубного базирования Воут F-8 «Крусейдер» (Vought F-8 Crusader, 1953 г.) и прототип бомбардировщика Martin XB-51 ( англ. ) (1949 г.) имели изменяемый в полёте угол установки крыла.

Угол альфа в треугольнике. Как найти угол в прямоугольном треугольнике

Здравствуйте!
Как найти угол в прямоугольном треугольнике? Расскажите, пожалуйста, как можно подробнее.
Спасибо!

Прежде, чем разобрать вопрос о том, как найти угол в прямоугольном треугольнике , рассмотрим основные свойства такого вида треугольников. Первое, что нас будет интересовать — это углы данного треугольника. Поскольку треугольник прямоугольный, то один его угол будет прямым, то есть равным 90 градусов. Известно, что если сложить все углы любого из треугольников, то получим 180 градусов. Соответственно, если один из углов в прямоугольном треугольнике равен 90 градусов, то сумма двух других будет равна 180 — 90 = 90 градусов. Следовательно, достаточно найти один из двух острых углов, и тогда легко можно вычислить и величину второго острого угла:
ugol1 = 90 — ugol2.
Зная две любые стороны прямоугольного треугольника и используя определения основных из тригонометрических функций, можно найти величину любого угла прямоугольного треугольника.
Например, если известна длина любого из катетов и длина гипотенузы, то можно вычислить синус или косинус одного из острых углов. А если даны длины обоих катетов. То можно вычислить значение тангенса или котангенса любого из острых углов.

Далее необходимо вычислить с помощью таблицы значений тригонометрических функций величину угла и рассчитать значение второго острого угла по выше упомянутой формуле:
ugol1 = 90 — ugol2.

Угол альфа, как определить. Таблица определения положения электрической оси сердца (по Дьеду)

Таблица определения угла альфа

Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.

При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.

Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме.

Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.

И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.

Пределы отклонения электрической оси сердца

Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.

Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса заменяют понятием «определяющий зубец» комплекса QRS, визуально сопоставляя по абсолютной величине зубцы R и S .

Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец R. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

Сопоставление зубцов R и S комплекса QRS

Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).

Схематично это условие записывается как RI-SIII.

Визуальное определение электрической оси сердца. Левограмма

Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма).

Упрощенно это условие записывается как SI-RIII.

Визуальное определение электрической оси сердца. Правограмма

Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.

Длина окружности

О чем эта статья:

6 класс, 9 класс, ЕГЭ/ОГЭ

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

r — радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π — математическая константа, примерно равная 3,14

a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла ( sin α ) — отношение противолежащего этому углу катета к гипотенузе.

Косинус угла ( cos α ) — отношение прилежащего катета к гипотенузе.

Тангенс угла ( t g α ) — отношение противолежащего катета к прилежащему.

Котангенс угла ( c t g α ) — отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).

Синус (sin) угла поворота

Синус угла поворота α — это ордината точки A 1 ( x , y ). sin α = y

Косинус угла поворота α — это абсцисса точки A 1 ( x , y ). cos α = х

Тангенс угла поворота α — это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x

Котангенс угла поворота α — это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y

Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , — 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.

Синус и косинус определены для любых углов α .

Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )

Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Начальная точка на окружности — точка A c координатами ( 1 , 0 ).

Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Синус (sin) числа t

Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y

Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x

Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Геометрия. Урок 1. Тригонометрия

Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Тригонометрия в прямоугольном треугольнике

Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.

sin α = Противолежащий катет гипотенуза

Косинус угла – отношение прилежащего катета к гипотенузе.

cos α = Прилежащий катет гипотенуза

Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).

tg α = Противолежащий катет Прилежащий катет

Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).

ctg α = Прилежащий катет Противолежащий катет

Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:

sin ∠ A = C B A B

cos ∠ A = A C A B

tg ∠ A = sin ∠ A cos ∠ A = C B A C

ctg ∠ A = cos ∠ A sin ∠ A = A C C B

sin ∠ B = A C A B

cos ∠ B = B C A B

tg ∠ B = sin ∠ B cos ∠ B = A C C B

ctg ∠ B = cos ∠ B sin ∠ B = C B A C

Тригонометрия: Тригонометрический круг

Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.

Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.

Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )

На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.

Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .

Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .

Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .

Рассмотрим прямоугольный треугольник A O B :

cos α = O B O A = O B 1 = O B

sin α = A B O A = A B 1 = A B

Поскольку O C A B – прямоугольник, A B = C O .

Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).

Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :

Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .

Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .

Координата по оси x – косинус угла , координата по оси y – синус угла .

Ещё одно замечание.

Синус тупого угла – положительная величина, а косинус – отрицательная.

Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .

Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .

Основное тригонометрическое тождество

sin 2 α + cos 2 α = 1

Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :

A B 2 + O B 2 = O A 2

sin 2 α + cos 2 α = R 2

sin 2 α + cos 2 α = 1

Тригонометрия: Таблица значений тригонометрических функций

0 °
30 °
45 °
60 °
90 °

sin α
0
1 2
2 2
3 2
1

cos α
1
3 2
2 2
1 2
0

tg α
0
3 3
1
3
нет

ctg α
нет
3
1
3 3
0

Тригонометрия: градусы и радианы

Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!

Тригонометрия: Формулы приведения

Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,

можно заметить, что:

sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °

sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °

sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °

sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °

cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °

cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °

cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °

cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °

Рассмотрим тупой угол β :

Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:

sin ( 180 ° − α ) = sin α

cos ( 180 ° − α ) = − cos α

tg ( 180 ° − α ) = − tg α

ctg ( 180 ° − α ) = − ctg α

Тригонометрия: Теорема синусов

В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.

a sin ∠ A = b sin ∠ B = c sin ∠ C

Тригонометрия: Расширенная теорема синусов

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R

Тригонометрия: Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A

b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B

c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с тригонометрией.

Тригонометрия: Тригонометрические уравнения

Это тема 10-11 классов.

Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!

[spoiler title=”источники:”]

http://b4.cooksy.ru/articles/kak-nayti-alfa-okruzhnosti

[/spoiler]

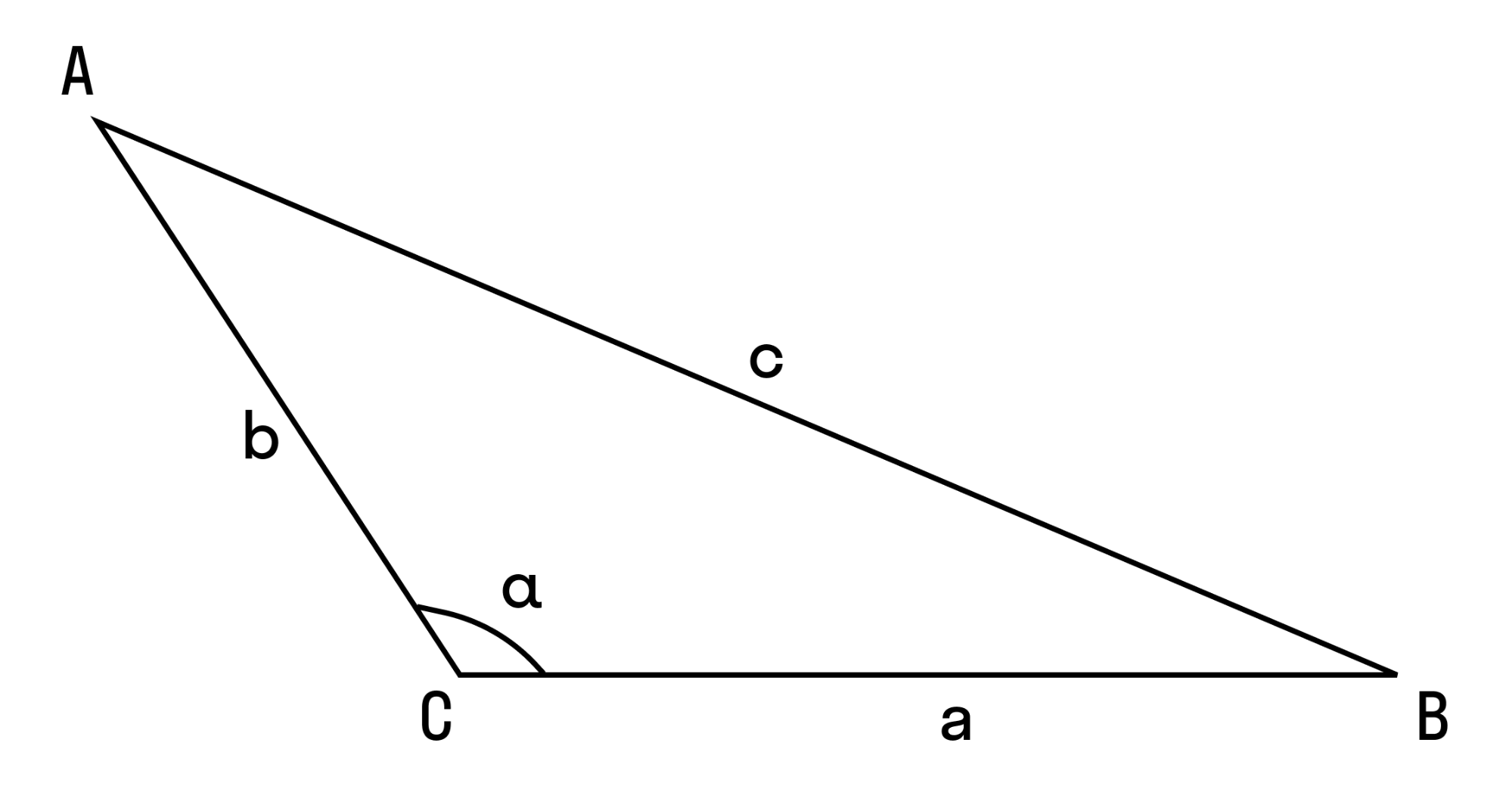
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

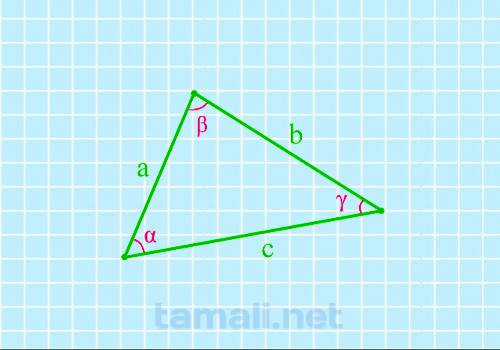
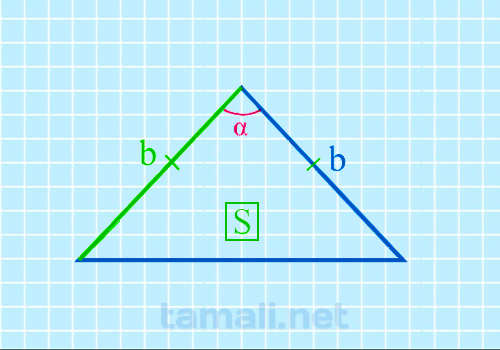
Угол прямоугольного треугольника через две стороны

Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

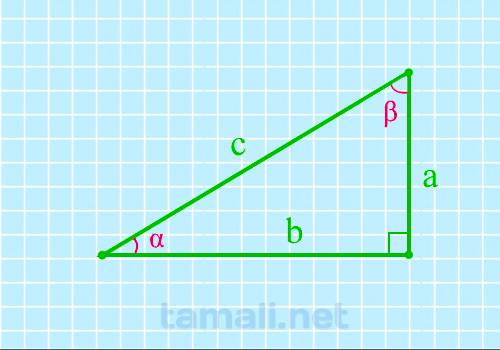
Острый угол прямоугольного треугольника через катет и площадь

Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

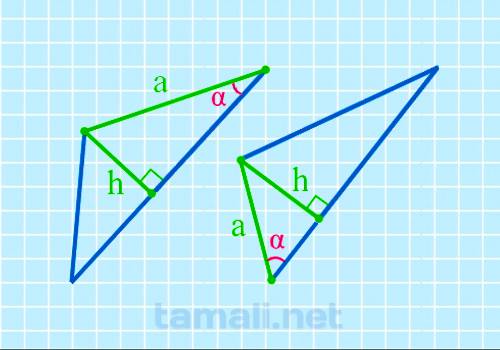
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

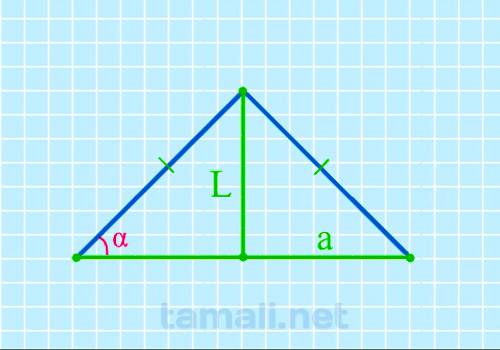
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

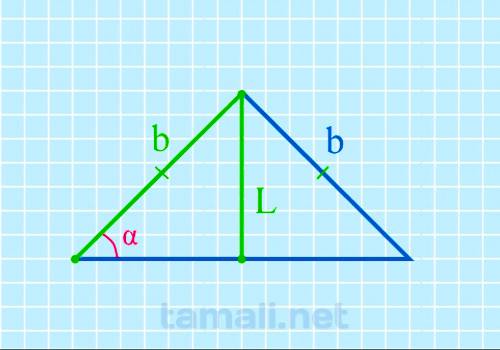
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

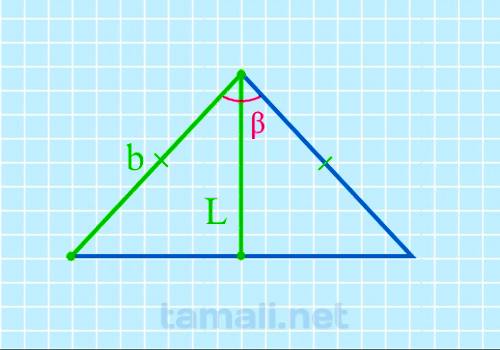
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.

Как найти угол альфа формула – Синус угла — sin(A) | Формулы и расчеты онлайн

В данной статье мы с вами разберём некоторые задачи связанные с выражениями. Задания данной группы довольно разнообразны. Если вы запомнили свойства степеней, корней и логарифмов, знаете основные формулы тригонометрии, и постоянно практикуетесь, то большинство задач для вас никакого труда не представят.

Относительную сложность могут вызывать следующие:

— преобразования буквенных иррациональных выражений
— вычисление значений тригонометрических выражений
— преобразования тригонометрических выражений

Если перечислить все группы задач, то они довольно разнообразны.

Они включают в себя: ПОКАЗАТЬ/СКРЫТЬ

Здесь мы с вами разберём задачи на вычисление значений тригонометрических выражений. Конечно, все их в одной статье разобрать невозможно. Но мы обязательно разберём и другие примеры, не пропустите!

Итак, что обязательно вы должны знать и всегда помнить? Это знаки тригонометрических функций в четвертях. ЭТО ВАЖНО.

Как осознать эту информацию и понять следствием чего она является – об этом будет отдельная статья (если вы это знаете, то прекрасно). Пока предлагаю пока просто запомнить:

Основное тригонометрическое тождество:

Формулы тангенса и котангенса:

Выполняются элементарные алгебраические преобразования:

1. Числитель и знаменатель дроби можем умножать и делить на одно и тоже число.
2. Левую и правую часть уравнения можем умножать и делить на одно и тоже число.

В представленных ниже заданиях используется основное тригонометрическое тождество и формула тангенса.

Найдите тангенс альфа, если

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

Косинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение синуса. Затем подставить их в формулу тангенса.

Теперь ВАЖНЫЙ момент: необходимо определить знак синуса для интервала (3Пи/2;2Пи). Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:

Найдите tg α, если

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

Cинус угла нам известен. Из формулы основного тригонометрического тождества мы можем найти значение косинуса. Затем подставить их в формулу тангенса.

Определяем знак косинуса для интервала (Пи/2;Пи). Это интервал от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное (смотрите эскиз). Поэтому

Найдите 5·cos α, если синус альфа

Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos 2 x = 1– sin 2 x и

Определим знак косинуса. Угол принадлежит интервалу (3Пи/2;2Пи).

Это интервал от 270 до 360 градусов (четвёртая четверть). Значение косинуса в этой четверти положительное, поэтому:

Таким образом, 5·cos α = 5∙0,7 = 3,5

Найдите 0,1·sin α, если

Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin 2 x = 1– cos 2 x и

Определим знак синуса. Угол принадлежит интервалу (0; Пи/2).

Это интервал от 0 до 90 градусов (первая четверть). Значение синуса в этой четверти положительное, поэтому:

Таким образом 0,1·sin α = 0,1∙0,3 = 0,03

Общая рекомендация для следующих данных примеров! Если требуется найти тангенс аргумента (квадрат тангенса), то осуществляем деление на косинус (квадрат косинуса). Если требуется найти котангенс аргумента (квадрат котангенса), то осуществляем деление на синус (квадрат синуса). Примеры:

65217. Найдите tg 2 α, если 3sin 2 α + 8 cos 2 α = 7

Требуется найти квадрат тангенса. Разделим обе части уравнения на cos 2 α, получим:

Далее по формуле основного тригонометрического тождества можно найти квадрат синуса и используя формулу тангенса вычислить уже его квадрат:

Преобразуем данное выражение так, чтобы в числителе и знаменателе был тангенс. Разделим числитель и знаменатель на cos α, получим:

Здесь дано значение тангенса. Необходимо сделать так, чтобы в выражении у нас был тангенс. Вынесем cosα за скобки в числителе и знаменателе (или разделим числитель и знаменатель на cosα), получим:

Подставим значение тангенса данное в условии, получим:

*Косинус у нас сократился.

65363. Найдите tg α, если

В левой части в числителе и знаменателе вынесем cosα за скобки, получим:

65423. Найдите tg α, если

Умножим обе части уравнения на 4 (2sinα+cosα+1)

26775. Найдите tg α, если

26776. Найдите tg α, если

26777. Найдите 3cos α, если

26778. Найдите 5sin α, если

26787. Найдите tg 2 α, если

26790. Найдите tg α, если

26791. Найдите tg α, если

Подведём итог, для решения подобных примеров вы:

1. Должны знать на зубок основные формулы тригонометрии.
2. Не забывать определять знак (+ или -) для тригонометрических функций в четвертях. Потерянный знак на экзамене – это ошибка и потерянный бал, будьте внимательны.

Надеюсь, что материал был для вас полезен.

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Определение ЭОС

Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.

Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях. Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец К — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°. Таблица определения положения электрической оси сердца (по Дьеду)

Таблица определения угла альфа

Если угол альфа находится в пределах 50—70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме. При отклонении электрической оси сердца вправо угол альфа будет определяться в пределах 70—90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса. Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме. Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме. И наконец, если значение у г л а альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.

Пределы отклонения электрической оси сердца

Определение отклонения электрической оси сердца по углу альфа с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой. Однако определить отклонение электрической оси сердца можно и без необходимых таблиц. В этом случае отклонение электрической оси находят по анализу зубцов R и S в I и III стандартных отведениях. При этом понятие алгебраической суммы зубцов желудочкового комплекса комплекса QRS, заменяют визуально понятием «определяющий зубец» сопоставляя по абсолютной величине зубцы R и S . Говорят о «желудочковом комплексе R-типа», подразумевая, что в данном желудочковом комплексе более высоким является зубец К. Напротив, в «желудочковом комплексе S-типа» определяющим зубцом комплекса QRS является зубец S.

Сопоставление зубцов К и 3 комплекса QRS

Если на электрокардиограмме в I стандартном отведении желудочковый комплекс представлен R-типом, а комплекс QRS в III стандартном отведении имеет форму S-типа, то в данном случае электрическая ось сердца отклонена влево (левограмма).

Схематично это условие записывается как RI-SIII.

Визуальное определение электрической оси сердца

. Левограмма Напротив, если в I стандартном отведении мы имеем S-тип желудочкового комплекса, а в III отведении R-тип комплекса QRS, то электрическая ось сердца отклонена вправо (правограмма). Упрощенно это условие записывается как SI-RIII.

Визуальное определение электрической оси сердца

. Правограмма Результирующий вектор возбуждения желудочков расположен в норме во фронтальной плоскости так, что его направление совпадает с направлением оси II стандартного отведения.

Нормальное положение электрической оси сердца

(нормограмма) На рисунке видно, что амплитуда зубца R во II стандартном отведении наибольшая. В свою очередь зубец К в I стандартном отведении превосходит зубец RIII. При таком условии соотношения зубцов R в различных стандартных отведениях мы имеем нормальное положение электрической оси сердца (электрическая ось сердца не отклонена). Краткая запись этого условия — RII>RI>RIII.

III.3. Угол альфа

III.3. Угол α

Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол α.

Величину угла α находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q+R+S) в T и III стандартных отведениях.

Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (-), поскольку находятся ниже изоэлектрической линии, а зубец R – знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла α. В нашем случае он равен мину с 70°.

Если угол α находится в пределах 50-70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.

При отклонении электрической ось сердца вправо угол α будет определяться в пределах 70-90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол α будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.

Определяя угол α в пределах 50-0°, говорят об отклонении электрической оси сердца влево, или о левограмме.

Изменение угла α в пределах 0 – минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.

И, наконец, если значение угла α будет меньше минус 30° (например, минус 45°) – говорят о блокаде передней ветви левой ножки пучка Гиса.

Определение отклонения электрической оси сердца по углу α с использованием таблиц и схем производят в основном врачи кабинетов функциональной диагностики, где соответствующие таблицы и схемы всегда под рукой.

Однако определить отклонение электрической оси сердца можно и без необходимых таблиц.

Как найти угол в окружности? ? Зная координаты двух точек.

Добрый день! Как найти угол альфа. Если у меня есть воображаемая окружность. Ее центр точка А. и Есть точка В. Мне нужно найти угол. По какой формуле искать. Также точка В может находиться ниже оси OZ, по формуле должен получать градус от 180 до 360.

Как, по какой? Угол равен 180 градусов + Arctg( (Yb — Ya) / (Xb — Xa) ). Если Xa = Xb, то вместо арктангенса прибавляешь 90 градусов.

Ох, насвистел. . .Тебе же нужно в промежутке от 180 до 360.

Тогда еще к этой формуле добавить, а если Arctg() < 0, то складывать его с 360 градусов, а не со 180.

на кой тут окружность и оси координат? Они никакого отношения к задаче вообще не имеют. Да вы еще для пущей путаницы назвали горизонталь OZ, будто это третья ось координат: )

у вас есть точки A и B и горизонталь. опустите из точки B перпендикуляр на линию OZ, получите точку С с координатами Bx, Ау. перед вами треугольник, ваш искомый угол — арксинус |AC| / |AB|

координаты точки А (Х1;У1) точки Б (Х2;У2)
из точку Б опускаешь перпендикуляр на ось ОЗ в точку С — получаем БС. получаешь прямоугольный треугольник.
длина БС = У2-У1. длина АС = Х2-Х1
получаешь длину гипотенузы АБ. получаешь площадь треугольника.
площадь треугольника также вычисляется
С = АБ*АБ + АС*АС — 2*АБ*АС*косинус (угла между сторонам АБ и АС)
отсюда вычисляешь косинус, а из него сам угол.

П. С. правда не понимаю зачем дана окружность. А если нужен угол больше 180, то к найденному прибавь просто 180.

Теорема косинусов и синусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2 < 0, угол α будет тупым.

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

• Если cos α > 0, то α ∈ (0°;90°)
• Если cos α < 0, то α ∈ (90°;180°)
• Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.

1. Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
   
2. Так как a 2 + b 2 < c 2 , то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

---

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.

• Окружность — линия, ограничивающая круг.
• Дуга — часть окружности.
• Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
• Хорда — отрезок, соединяющий две точки окружности.
• Сегмент — часть круга, ограниченная хордой и дугой.
• Сектор — часть круга, ограниченная двумя радиусами и дугой.

---

Интересующие нас величины и их обозначения:

---

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

• Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
• Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
• Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

---

1. Даны диаметр D и длина дуги L

;     длина хорды ;
высота сегмента ;    центральный угол .

---

2. Даны диаметр D и длина хорды X

;     длина дуги ;
высота сегмента ;    центральный угол .

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол .

---

3. Даны диаметр D и центральный угол φ

;     длина дуги ;
длина хорды ;    высота сегмента .

---

4. Даны диаметр D и высота сегмента H

;     длина дуги ;
длина хорды ;    центральный угол .

---

6. Даны длина дуги L и центральный угол φ

;     диаметр ;
длина хорды ;    высота сегмента .

---

8. Даны длина хорды X и центральный угол φ

;     длина дуги ;
диаметр ;    высота сегмента .

---

9. Даны длина хорды X и высота сегмента H

;     длина дуги ;
диаметр ;    центральный угол .

---

10. Даны центральный угол φ и высота сегмента H

;     диаметр ;
длина дуги ;    длина хорды .

---

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X

7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
; — в варианте 5
; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

---

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности ;
площадь круга ;
площадь сектора ;
площадь сегмента ;

---

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Программа Segment