Как найти угол альфа в сегменте

Как найти угол альфа в сегменте

Сегмент круга
Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
S=frac{1}{2}R^2(alpha-sin{alpha}) [1]
Длина дуги:
L={alpha}R
Длина хорды:
c=2{R}{sin{frac{alpha}{2}}}
Высота сегмента:
h={R}left(1-{cos{frac{alpha}{2}}}right)

PLANETCALC, Сегмент

Сегмент

Угол в градусах, образуемый радиусами сектора

Точность вычисления

Знаков после запятой: 2

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

PLANETCALC, Параметры сегмента по хорде и высоте

Параметры сегмента по хорде и высоте

Точность вычисления

Знаков после запятой: 2

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
R=frac{h}{2}+frac{c^2}{8h}

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:
alpha=2arcsin{ frac{c}{2R} }
Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

PLANETCALC, Площадь сегмента круга по радиусу и высоте

Площадь сегмента круга по радиусу и высоте

Точность вычисления

Знаков после запятой: 2

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
alpha=2arccosleft(1-frac{h}{R}right)
далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

  • длина дуги
  • угол
  • хорда
  • высота
  • радиус
  • площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

PLANETCALC, Круговой сегмент - все варианты расчета

Круговой сегмент – все варианты расчета

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Источник

Геометрия круга

Круг, его части, их размеры и соотношения — вещи, с которыми ювелир постоянно сталкивается. Кольца, браслеты, касты, трубки, шары, спирали — много всего круглого приходится делать. Как же всё это посчитать, особенно если тебе посчастливилось в школе прогулять уроки геометрии?..

Давайте сначала рассмотрим, какие у круга бывают части и как они называются.Круг и его части

  • Окружность — линия, ограничивающая круг.
  • Дуга — часть окружности.
  • Радиус — отрезок, соединяющий центр круга с какой-либо точкой окружности.
  • Хорда — отрезок, соединяющий две точки окружности.
  • Сегмент — часть круга, ограниченная хордой и дугой.
  • Сектор — часть круга, ограниченная двумя радиусами и дугой.

Интересующие нас величины и их обозначения:

Теперь посмотрим, какие задачи, связанные с частями круга, приходится решать.

  • Найти длину развертки какой-либо части кольца (браслета). Задан диаметр и хорда (вариант: диаметр и центральный угол), найти длину дуги.
  • Есть рисунок на плоскости, надо узнать его размер в проекции после сгибания в дугу. Заданы длина дуги и диаметр, найти длину хорды.
  • Узнать высоту детали, полученной сгибанием плоской заготовки в дугу. Варианты исходных данных: длина дуги и диаметр, длина дуги и хорда; найти высоту сегмента.

Жизнь подскажет и другие примеры, а эти я привел только для того, чтобы показать необходимость задания каких-нибудь двух параметров для нахождения всех остальных. Вот этим мы и займемся. А именно, возьмем пять параметров сегмента: D, L, X, φ и H. Затем, выбирая из них все возможные пары, будем считать их исходными данными и путем мозгового штурма находить все остальные.

Чтобы зря не грузить читателя, подробных решений я приводить не буду, а приведу лишь результаты в виде формул (те случаи, где нет формального решения, я оговорю по ходу дела).

И еще одно замечание: о единицах измерения. Все величины, кроме центрального угла, измеряются в одних и тех же абстрактных единицах. Это значит, что если, к примеру, вы задаёте одну величину в миллиметрах, то другую не надо задавать в сантиметрах, а результирующие значения будут измеряться в тех же миллиметрах (а площади — в квадратных миллиметрах). То же самое можно сказать и про дюймы, футы и морские мили.

И только центральный угол во всех случаях измеряется в градусах и ни в чём другом. Потому что, как показывает практика, люди, проектирующие что-нибудь круглое, не склонны измерять углы в радианах. Фраза «угол пи на четыре» многих ставит в тупик, тогда как «угол сорок пять градусов» — понятна всем, так как это всего на пять градусов выше нормы. Однако, во всех формулах будет присутствовать в качестве промежуточной величины еще один угол — α. По смыслу это половина центрального угла, измеренная в радианах, но в этот смысл можно спокойно не вникать.

1. Даны диаметр D и длина дуги L

alpha~=~L/D;     длина хорды X~=~D~*~sin alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~{360/pi}.

2. Даны диаметр D и длина хорды X

alpha~=~arcsin X/D;     длина дуги L~=~D~*~alpha;
высота сегмента H~=~D~*~{1~-~cos alpha}/2;    центральный угол varphi~=~alpha~*~ {360/pi}.

Поскольку хорда делит круг на два сегмента, у этой задачи не одно, а два решения. Чтобы получить второе, нужно в приведенных выше формулах заменить угол α на угол alpha_1~=~pi~-~alpha.

3. Даны диаметр D и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

4. Даны диаметр D и высота сегмента H

alpha~=~arccos(1~-~{{2H}/D});     длина дуги L~=~D~*~alpha;
длина хорды X~=~D~*~sin alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

6. Даны длина дуги L и центральный угол φ

alpha~=~varphi~*~{pi/360};     диаметр D~=~L/alpha;
длина хорды X~=~D~*~sin alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

8. Даны длина хорды X и центральный угол φ

alpha~=~varphi~*~{pi/360};     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    высота сегмента H~=~D~*~{1~-~cos alpha}/2.

9. Даны длина хорды X и высота сегмента H

alpha~=~2~*~arctg~{2H}/X;     длина дуги L~=~X~*~alpha/{sin alpha};
диаметр D~=~L/alpha;    центральный угол varphi~=~alpha~*~{360/pi}.

10. Даны центральный угол φ и высота сегмента H

alpha~=~varphi~*~{pi/360};     диаметр D~=~{2 H}/{1~-~cos alpha};
длина дуги L~=~D~*~alpha;    длина хорды X~=~D~*~sin alpha.

Внимательный читатель не мог не заметить, что я пропустил два варианта:

5. Даны длина дуги L и длина хорды X
7. Даны длина дуги L и высота сегмента H

Это как раз те два неприятных случая, когда у задачи нет решения, которое можно было бы записать в виде формулы. А задача-то не такая уж редкая. Например, у вас есть плоская заготовка длины L, и вы хотите согнуть ее так, чтобы ее длина стала X (или высота стала H). Какого диаметра взять оправку (ригель)?

Задача эта сводится к решению уравнений:
L~*~sin alpha~=~X~*~alpha; — в варианте 5
L~*~(1~-~cos alpha)~=~2 H~*~alpha; — в варианте 7
и хоть они и не решаются аналитически, зато легко решаются программным способом. И я даже знаю, где взять такую программу: на этом самом сайте, под именем Segment. Всё то, что я тут длинно рассказываю, она делает за микросекунды.

Для полноты картины добавим к результатам наших вычислений длину окружности и три значения площадей — круга, сектора и сегмента. (Площади нам очень помогут при вычислении массы всяких круглых и полукруглых деталей, но об этом — в отдельной статье.) Все эти величины вычисляются по одним и тем же формулам:

длина окружности C~=~pi~*~D;
площадь круга S~=~pi~*~D^2/4;
площадь сектора S_sect~=~S~*~{varphi/360};
площадь сегмента S_segm~=~S_sect~-~{X~*~D~*~cos alpha}/4;

И в заключение еще раз напомню о существовании абсолютно бесплатной программы, которая выполняет все перечисленные вычисления, освобождая вас от необходимости вспоминать, что такое арктангенс и где его искать.

Программа Segment

Источник

Мысленно
поместим результирующий вектор
возбуждения желудочков внутрь треугольника
Эйнтховена. Угол, образованный направлением
результирующего вектора и осью I
стандартного отведения, и есть искомый
угол альфа.

Величину
угла альфа находят по специальным
таблицам или схемам, предварительно
определив на электрокардиограмме
алгебраическую сумму зубцов желудочкового
комплекса (Q + R + S) в I и III стандартных
отведениях.

Найти
алгебраическую сумму зубцов желудочкового
комплекса достаточно просто: измеряют
в миллиметрах величину каждого зубца
одного желудочкового комплекса QRS,
учитывая при этом, что зубцы Q и S имеют
знак минус (—), поскольку находятся ниже
изоэлектрической линии, а зубец К —
знак плюс (+). Если какой-либо зубец на
электрокардиограмме отсутствует, то
его значение приравнивается к нулю
(0).

Далее,
сопоставляя найденную алгебраическую
сумму зубцов для I и III стандартных
отведений, по таблице определяют значение
угла альфа. В нашем случае он равен минус
70°.

Таблица
определения положения электрической
оси сердца (по Дьеду)

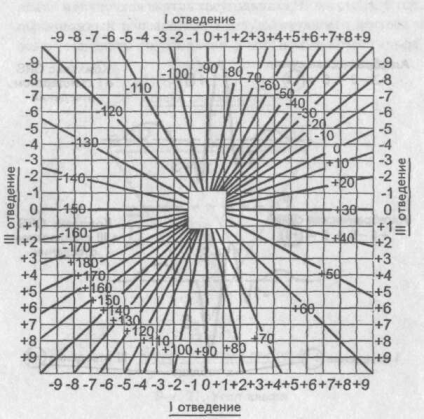
Рис.
29.

Таблица
определения угла альфа

Если
угол альфа находится в пределах 50—70°,
говорят о нормальном положении
электрической оси сердца (электрическая
ось сердца не отклонена), или
нормограмме.

При
отклонении электрической оси сердца
вправо угол альфа будет определяться
в пределах 70—90°. В обиходе такое положение
электрической оси сердца называют
правограммой.

Если
угол альфа будет больше 90° (например,
97°), считают, что на данной ЭКГ имеет
место блокада задней ветви левой ножки
пучка Гиса.

Определяя
угол альфа в пределах 50—0° говорят об
отклонении электрической оси сердца
влево, или о левограмме.

Изменение
угла альфа в пределах 0 — минус 30°
свидетельствует о резком отклонении
электрической оси сердца влево или,
иными словами, о резкой левограмме.

И
наконец, если значение у г л а альфа
будет меньше минус 30° (например, минус
45°) — говорят о блокаде передней ветви
левой ножки пучка Гиса.

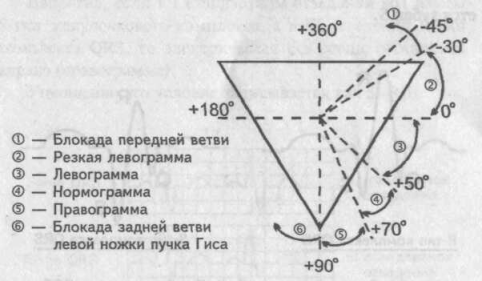
Рис.
30.

Пределы
отклонения электрической оси сердца

Определение
отклонения электрической оси сердца
по углу альфа с использованием таблиц
и схем производят в основном врачи
кабинетов функциональной диагностики,
где соответствующие таблицы и схемы
всегда под рукой.

Однако
определить отклонение электрической
оси сердца можно и без необходимых
таблиц.

В
этом случае отклонение электрической
оси находят по анализу зубцов R и S в I и
III стандартных отведениях. При этом
понятие алгебраической суммы зубцов
желудочкового комплекса комплекса QRS,
заменяют визуально понятием «определяющий
зубец» сопоставляя по абсолютной
величине зубцы R и S .

Говорят
о «желудочковом комплексе R-типа»,
подразумевая, что в данном желудочковом
комплексе более высоким является зубец
К. Напротив, в «желудочковом комплексе
S-типа» определяющим зубцом комплекса
QRS является зубец S.

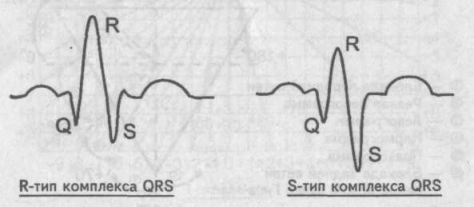
Рис.
31.

Сопоставление
зубцов К и 3 комплекса QRS

Если
на электрокардиограмме в I стандартном
отведении желудочковый комплекс
представлен R-типом, а комплекс QRS в III
стандартном отведении имеет форму
S-типа, то в данном случае электрическая
ось сердца отклонена влево (левограмма).

Схематично
это условие записывается как RI-SIII.

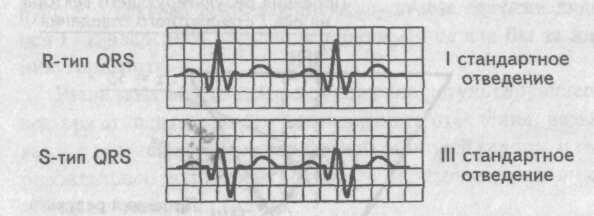
Рис.
32.

Визуальное
определение электрической оси сердца

.
Левограмма

Напротив,
если в I стандартном отведении мы имеем
S-тип желудочкового комплекса, а в III
отведении R-тип комплекса QRS, то
электрическая ось сердца отклонена
вправо (правограмма).

Упрощенно
это условие записывается как SI-RIII.

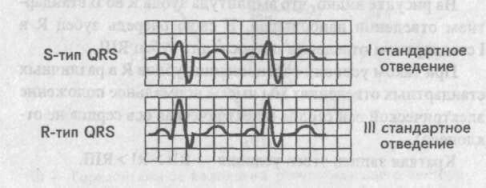
Рис.
33.

Визуальное
определение электрической оси сердца

.
Правограмма

Результирующий
вектор возбуждения желудочков расположен
в норме во фронтальной плоскости так,
что его направление совпадает с
направлением оси II стандартного
отведения.

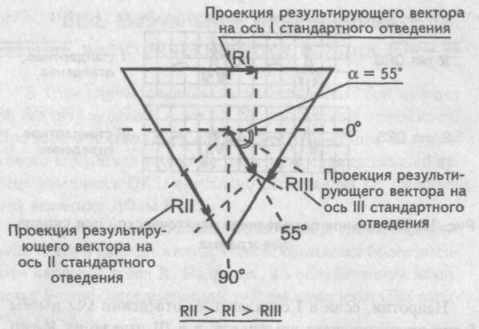
Рис.
34.

Нормальное
положение электрической оси сердца

(нормограмма)

На
рисунке видно, что амплитуда зубца R во
II стандартном отведении наибольшая. В
свою очередь зубец К в I стандартном
отведении превосходит зубец RIII.

При
таком условии соотношения зубцов R в
различных стандартных отведениях мы
имеем нормальное положение электрической
оси сердца (электрическая ось сердца
не отклонена).

Краткая
запись этого условия — RII>RI>RIII.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Однако когда сердце отклоняется от своего нормального анатомического положения в грудной клетке (астеническое и гиперстеническое телосложения, гипертрофия желудочков, заболевания легких и др.), передняя и задняя стенки могут быть представлены другими отделами сердца. Это необходимо учитывать для точной топической диагностики патологических процессов, происходящих в том или ином отделе сердца.

Помимо топической диагностики патологического процесса в различных отделах миокарда, электрокардиографические отведения позволяют проследить отклонение электрической оси сердца и определить его электрическую позицию. Об этих понятиях мы и поговорим ниже.

Глава III

Электрическая ось и электрическая позиция сердца

III.1. Результирующий вектор

Электрическая ось и электрическая позиция сердца неразрывно связаны с понятием результирующего вектора возбуждения желудочков во фронтальной плоскости.

Результирующий вектор возбуждения желудочков представляет собой сумму трех моментных векторов возбуждения: межжелудочковой перегородки, верхушки и основания сердца. Этот вектор имеет определенную направленность в пространстве, которое мы интерпретируем в трех плоскостях: фронтальной, горизонтальной и сагиттальной. В каждой из них результирующий вектор имеет свою проекцию.

Рис. 26. Проекция вектора в различных плоскостях

III.2. Электрическая ось сердца

Электрической осью сердца называется проекция результирующего вектора возбуждения желудочков во фронтальной плоскости.

Электрическая ось сердца может отклоняться от своего нормального положения либо влево, либо вправо.

Точное отклонение электрической оси сердца определяют по углу альфа (α).

III.3. Угол α

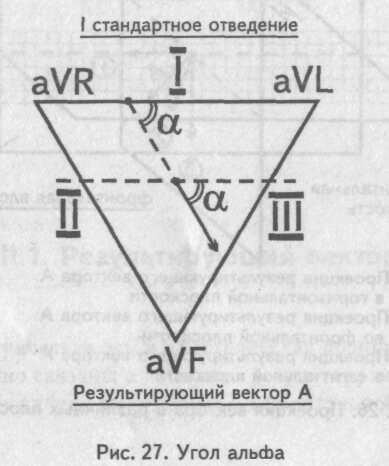
Мысленно поместим результирующий вектор возбуждения желудочков внутрь треугольника Эйнтховена. Угол, образованный направлением результирующего вектора и осью I стандартного отведения, и есть искомый угол альфа.

Рис. 27. Угол альфа.

Величину угла альфа находят по специальным таблицам или схемам, предварительно определив на электрокардиограмме алгебраическую сумму зубцов желудочкового комплекса (Q + R + S) в I и III стандартных отведениях.

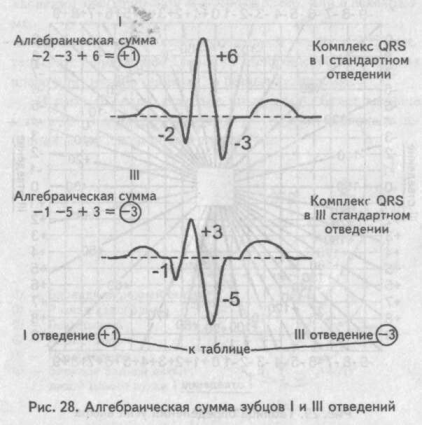
Найти алгебраическую сумму зубцов желудочкового комплекса достаточно просто: измеряют в миллиметрах величину каждого зубца одного желудочкового комплекса QRS, учитывая при этом, что зубцы Q и S имеют знак минус (—), поскольку находятся ниже изоэлектрической линии, а зубец R — знак плюс (+). Если какой-либо зубец на электрокардиограмме отсутствует, то его значение приравнивается к нулю (0).

Рис. 28. Алгебраическая сумма зубцов I и III отведений

Далее, сопоставляя найденную алгебраическую сумму зубцов для I и III стандартных отведений, по таблице определяют значение угла альфа. В нашем случае он равен минус 70°.

Таблица определения положения электрической оси сердца (по Дьеду)

Рис. 29. Таблица определения угла альфа

Если угол альфа находится в пределах 50–70°, говорят о нормальном положении электрической оси сердца (электрическая ось сердца не отклонена), или нормограмме.

При отклонении электрической ось сердца вправо угол альфа будет определяться в пределах 70–90°. В обиходе такое положение электрической оси сердца называют правограммой.

Если угол альфа будет больше 90° (например, 97°), считают, что на данной ЭКГ имеет место блокада задней ветви левой ножки пучка Гиса.

Определяя угол альфа в пределах 50—0° говорят об отклонении электрической оси сердца влево, или о левограмме.

Изменение угла альфа в пределах 0 — минус 30° свидетельствует о резком отклонении электрической оси сердца влево или, иными словами, о резкой левограмме.

И наконец, если значение угла альфа будет меньше минус 30° (например, минус 45°) — говорят о блокаде передней ветви левой ножки пучка Гиса.

Рис. 30. Пределы отклонения электрической оси сердца

Источник

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте

его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву

, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения

и указать конкретные затруднения.

Обязательно просмотрите тему

Правила данного раздела, иначе Ваша тема может быть удалена

или перемещена в Карантин, а Вы так и не узнаете, почему.

 

Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 15:49 


09/04/12
4

всем доброго времени суток. не знаю туда ли обратился, но может кто поможет. ситуация, относящаяся скорее к геометрии. так вот. как найти угол альфа, зная, что площадь всего круга это единица и зная соотношение площадей S1 и S2?
я решал эту проблему методом подбора в графической программе. если S1=0,7, а S2=0,3, то угол альфа получался 109 градусов. нельзя ли вывести конкретную формулу? чтобы при каждых S1 и S2 можно было узнать альфа?

Изображение

Профиль  

Yu_K 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 16:17 


02/11/08
1183

Профиль  

svv 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 16:24 
Заслуженный участник


23/07/08
10073
Crna Gora

Yu_K

, сегментов секторов.

Профиль  

mvd 

 Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 16:40 


09/04/12
4

Профиль  

Sapsar 

 Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 16:55 


06/04/12
∞
33

(Оффтоп)

there is no “халява” here

— 09.04.2012, 17:59 —

Кстати, соотношение площадей чего именно?-из рисунка не совсем понятно, то ли сегмент, то ли сектор

Профиль  

mvd 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 17:06 


09/04/12
4

(Оффтоп)

there is no “халява” here

— 09.04.2012, 17:59 —

Кстати, соотношение площадей чего именно?-из рисунка не совсем понятно, то ли сегмент, то ли сектор

странно, по моему, по рисунку как раз понятно. цветами (красным и синим) выделено то, что известно

Профиль  

ИСН 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 17:53 
Заслуженный участник
Аватара пользователя


18/05/06
13417
с Территории

там трансцендентное, это только численно.

Профиль  

Maslov 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 18:19 
Заслуженный участник


09/08/09
3438
С.Петербург

Судя по этому

зная, что площадь всего круга это единица

и этому

если S1=0,7, а S2=0,3, то угол альфа получался 109 градусов

S1 и S2 — это площади секторов, и $alpha = 2 pi S2$
Правда, точное значение получается 108.

Профиль  

Sapsar 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 18:49 


06/04/12
∞
33

ага, значит там секторы
А зачем нам дают вторую площадь, если она вычисляется из первой?(ведь сумма единица)
В конечном счете получится уравнение с иксом и синусом, которое решается только численно(как отметил ИСН

)

Профиль  

ИСН 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение09.04.2012, 18:50 
Заслуженный участник
Аватара пользователя


18/05/06
13417
с Территории

Судя по этому (…)

Или так. Это если там всё-таки сектора. Правда, это противоречит и рисунку, и словесному описанию задачи. Зато версия, что это сегменты, противоречит приведённым численным данным. Видите, как важно не давать лишней информации.

Профиль  

Yu_K 

 Re: Нахождение угла через отношение площади сегмента и круга

Сообщение10.04.2012, 07:13 


02/11/08
1183

Профиль  

gris 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение10.04.2012, 07:29 
Заслуженный участник
Аватара пользователя


13/08/08
14204

Во всём виноват jpg. Автор вначале изобразил горизонтальную хорду в виде двойной сине-красной линии, но при преобразовании в упомянутый графический формат цвета смешались, и это вызвано разброд и шатания.
В подобных иллюстрациях лучше использовать заливку, либо увеличить толщину линий и использовать формат gif.

Профиль  

Yu_K 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение10.04.2012, 07:42 


02/11/08
1183

всем доброго времени суток. не знаю туда ли обратился, но может кто поможет. ситуация, относящаяся скорее к геометрии. так вот. как найти угол альфа, зная, что площадь всего круга это единица и зная соотношение площадей S1 и S2?
я решал эту проблему методом подбора в графической программе. если S1=0,7, а S2=0,3

– можно и так понять что угол равен 0.3 от полной окружности и тогда это 108 градусов и нет надобности огород городить…

(Оффтоп)

Профиль  

mvd 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение11.04.2012, 12:36 


09/04/12
4

всем доброго времени суток. не знаю туда ли обратился, но может кто поможет. ситуация, относящаяся скорее к геометрии. так вот. как найти угол альфа, зная, что площадь всего круга это единица и зная соотношение площадей S1 и S2?
я решал эту проблему методом подбора в графической программе. если S1=0,7, а S2=0,3

– можно и так понять что угол равен 0.3 от полной окружности и тогда это 108 градусов и нет надобности огород городить…

(Оффтоп)

можно и так понять? по какой такой логике? может вы мне также сходу в уме посчитаете сколько угол будет при S1=0,15 и S2=0,85? ладно бы решил тут что-то, а потом умничал, а то сидит тут сопли пузырями, а сам не дальше остальных вывел.

Профиль  

Toucan 

Re: Нахождение угла через отношение площади сегмента и круга

Сообщение11.04.2012, 12:42 
Админ форума
Аватара пользователя


19/03/10
8952

 ! 		 mvd, предупреждение за грубость и переход на личности

Профиль  

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Добавить комментарий