Skip to content
Home » База знаний » Найдите угол ABC равнобедренной трапеции ABCD
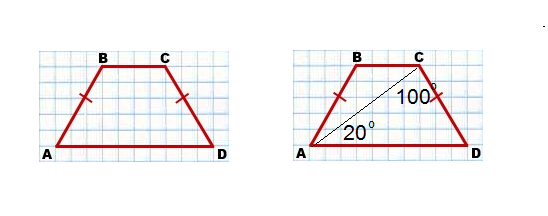
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ АС образует с основание AD и боковой стороной CD, углы равные 20 и 100 соответственно градусов.
Решение:
Из треугольника ACD находим угол CDA:
Сумма углов в треугольнике равна 180 градусов
180°-20°-100°=60° (угол CDA)
Угол АСВ равен углу CAD (накрест лежащие углы)
Угол АСВ=20°
Угол ABC равен углу BCD, потому что трапеция равнобедренная. Найдем угол BCD:
20°+100°=120°
Ответ: угол ABC равен 120 градусов.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Тип 15 № 311455
i
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Спрятать решение
Решение.
Сумма углов треугольника ACD равна 180°, поэтому Так как основания трапеции параллельны, углы CAD и BCA равны как накрестлежащие. Так как трапеция равнобедренная, сумма её противоположных углов равна 180°, поэтому
Ответ: 110.
Аналоги к заданию № 63: 311455 311456 Все
Источник: ГИА-2013. Математика. Экзамен. Вариант 1
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Трапеция — геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.
Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.
- Угол трапеции при основании через высоту и прилегающую
боковую сторону - Угол трапеции через нижнее основание, боковую сторону и
диагональ - Угол равнобедренной трапеции через нижнее основание,
среднию линию и боковую сторону - Угол равнобедренной трапеции через среднию линию, верхнее
основание и боковую сторону - Острый угол при нижнем основании прямоугольной трапеции
через высоту и два основания - Острый угол при нижнем основании прямоугольной трапеции
через два основания и боковую сторону
Угол трапеции при основании через высоту и прилегающую боковую сторону
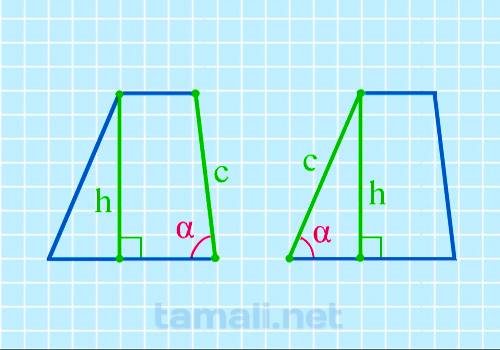
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы
sin α = h/с
где: h — высота трапеции, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.
Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции
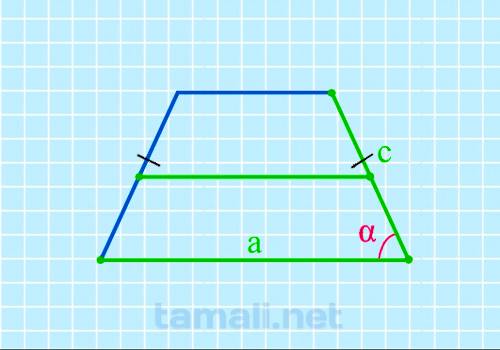
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:
cos α = (2a-2m) / 2c
где а — нижнее основание, m — средняя линия, с — боковая сторона.
Цифр после
запятой:
Результат в:
Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.
Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали
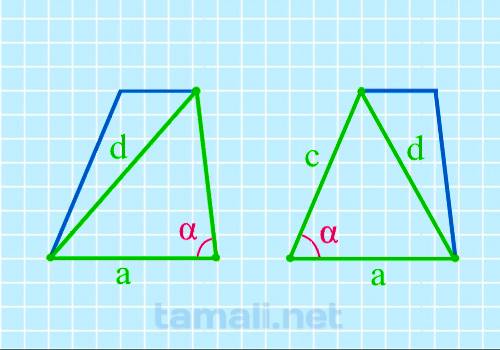
Если известны эти величины, воспользуемся формулой:
cos α= (a²+c²-d²) / 2ac
где а-нижнее основание, d-диагональ, с-боковая сторона.
Цифр после
запятой:
Результат в:
Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.
Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции
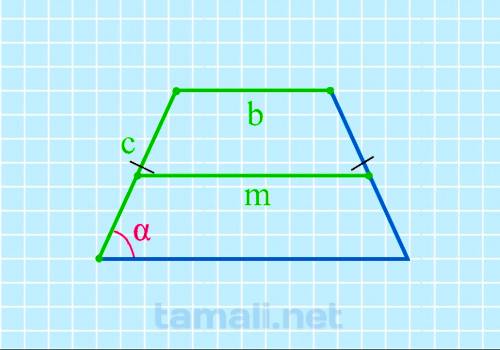
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:
cos α = (2m-2b) / 2c
где m — средняя линия, b — верхнее основание, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º
Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции
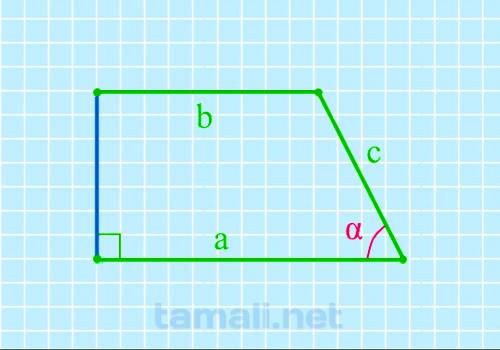
Находится по формуле
cos α = (a — b) / c
где a,b — основания, c — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º
Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции
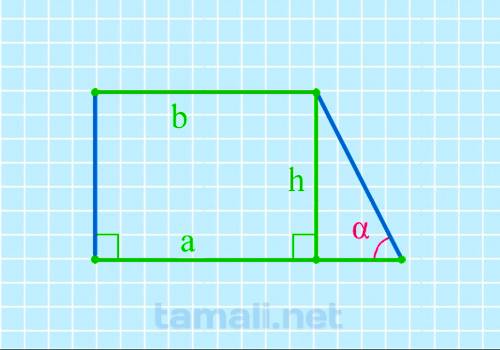
При известных указанных величинах воспользуемся следующей формулой:
tg(α) = h / (a-b)
где h — высота, a,b — верхнее и нижнее основания.
Цифр после
запятой:
Результат в:
Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.
Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.
Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.
-
Геометрия
Предыдущий вопрос
Следующий вопрос
fjdkfjskj
9 лет назад
Ответ
Ответ дан
gooz
Уг.ACB=уг.CAD30′(как накрест лежащие).
уг.BCD=80’+30’=110′
уг.ABC=уг.BCD=110′(так как трапеция равнобедренная).
Ответ
Проверено экспертом
Ответ дан
Hrisula
Основания трапеции – параллельны, АС – секущая, следовательно, накрестлежащие углы САД и АСВ=30°. равны.
∠АСВ+∠АСД=30°+80°=110°
Тупые углы трапеции АВС и ВСД равны, так как трапеция равнобедренная
∠АВС=110°
Ответы и объяснения
- fjdkfjskj
Не тот ответ, который тебе нужен?
Найди нужный
Условие
Найдите угол ABC равнобедренной трапеции ABCD если диагональ AC образует с основанием AD и боковой стороной CD углы равные 20 градусов и 100 градусов соответственно.
предмет не задан
14910
Решение
★
В равнобедренной трапеции углы при основании равны
∠ А= ∠ D
В треугольнике сумма углов равна 180 градусов.
В треугольнике ACD:
∠ СAD+ ∠ ACD+ ∠D=180 градусов
20 градусов + 100 градусов + ∠ D=180 градусов
∠ D=60 градусов.
∠ А=∠ D=60 градусов.
Сумма углов, прилежащих к боковой стороне трапеции равна 180 градусов.
∠ АВС= ∠ ВСD=120 градусов