Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
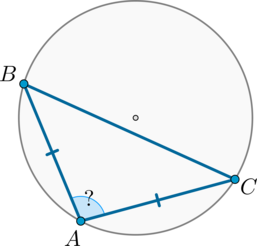
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
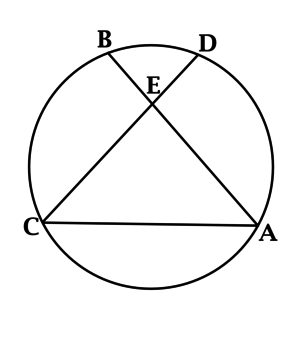
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
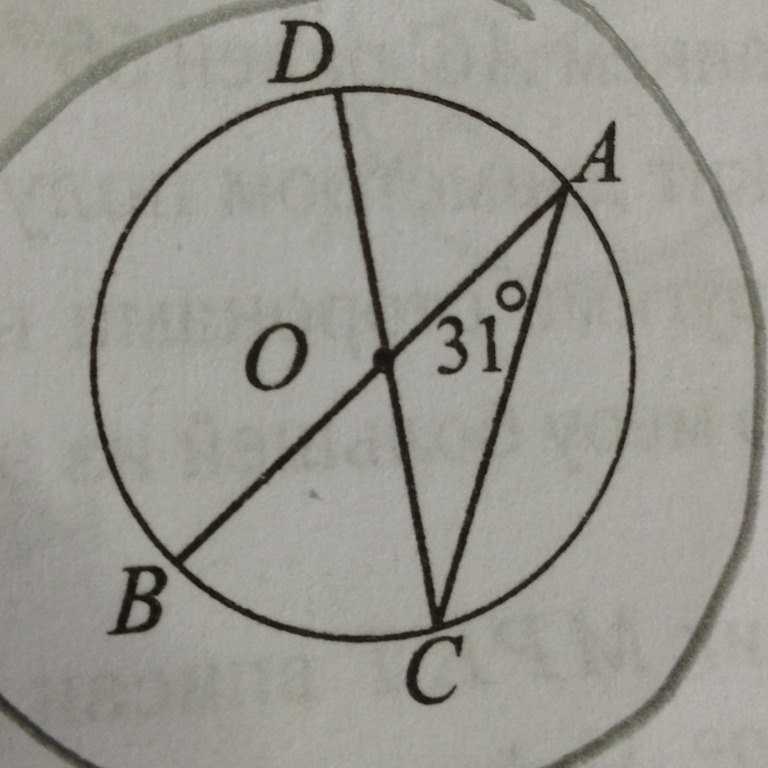
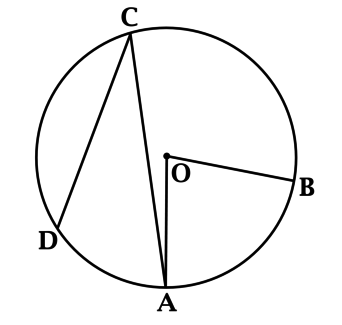
Вписанный угол BAC окружности с центром О равен 31градусов найдите величину угла BOD ответ дайте в градусах?
Математика | 5 – 9 классы
Вписанный угол BAC окружности с центром О равен 31градусов найдите величину угла BOD ответ дайте в градусах.
∠ВОС = 2∠ВАС = 62° (центральный, опирается на ту же дугу, что и вписанный)
∠BOD = 180° – ∠BOC = 180 – 62 = 128°(смежные).
Отрезки AC и BD – диаметры окружности с центром О?
Отрезки AC и BD – диаметры окружности с центром О.
Угол ACB равен 16 градусов.
Найдите угол AOD.
Ответ дайте в градусах.
В окружности с центром O AC и BD — диаметры?
В окружности с центром O AC и BD — диаметры.
Центральный угол AOD равен 100°.
Найдите вписанный угол ACB.
Ответ дайте в градусах.
Четырехугольник ABCD вписан в окружность?
Четырехугольник ABCD вписан в окружность.
Угол ABC равен 136 градусов, угол CAD равен 82 градуса.
Найдите угол ABD.
Ответ дайте в градусах.
В угол C величиной 18 вписана окружность которая касается сторон угла в точках A и B точка О центр окружности Найдите угол АОВ Ответ дайте в градусах?
В угол C величиной 18 вписана окружность которая касается сторон угла в точках A и B точка О центр окружности Найдите угол АОВ Ответ дайте в градусах.
Сторона АС треугольника АВС проходит через центр описанной около него окружности?
Сторона АС треугольника АВС проходит через центр описанной около него окружности.
Найдите угол С, если угол А равен 47 градусов.
Ответ дайте в градусах.
В окружности с центрем О отрезки АС и BD – диаметры?
В окружности с центрем О отрезки АС и BD – диаметры.
Угол AOD равен 108 градусам.
Найдите угол ACB.
Ответ дайте в градусах.
Найдите величину центрального угла , если вписанный угол , опирающийся на ту же дугу , равен 76 градусов ответ дайте в градусах?
Найдите величину центрального угла , если вписанный угол , опирающийся на ту же дугу , равен 76 градусов ответ дайте в градусах.
Точка О – центр окружности, вписанной в треугольник АВС, угол А = 60?
Точка О – центр окружности, вписанной в треугольник АВС, угол А = 60.
Найдите угол ВАО, ответ дайте в градусах.
Угол АСВ, равный 76 градусов, вписана окружность с центром О, имеющая со сторонами угла АСВ точки касания А и В?
Угол АСВ, равный 76 градусов, вписана окружность с центром О, имеющая со сторонами угла АСВ точки касания А и В.
Найдите велечину угла АОВ.
Ответ дайте в градусах.
Точка О – центр окружности?
Точка О – центр окружности.
Угол ВОС равен 160 градусов.
Найдите величину угла ВАС.
Вы открыли страницу вопроса Вписанный угол BAC окружности с центром О равен 31градусов найдите величину угла BOD ответ дайте в градусах?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 5 – 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.
Да, они могут быть взаимно простыми).
– 4 (2, 5a – 1, 5) + 5, 5a – 8 – 10a + 6 + 5, 5a – 8 – 4, 5a – 2 – 4, 5 * ( – 2 / 9) – 2 – 45 / 10 * ( – 2 / 9) – 2 (45 * 2 / 10 * 9) – 2 (5×2 / 10 * 1) – 2 (2 / 2) – 2 1 – 2 = – 1.
5 рублей ты должен дать Допустим у тебя 5 и у меня 5. Ты мне даешь 5 и у меня теперь 10 5 + 5 = 10 рубл У тебя 0 рубл. 0<10.
– 6, 6 : (2 5 / 7 * ( – 1, 5)) – 2 17 / 85 = – 6, 6 : ( 19 / 7 * ( – 15 / 10)) – 187 / 85 = – 6, 6 : ( – 57 / 14) – 187 / 85 = ( – 66 / 10) * ( – 14 / 57) – 187 / 85 = 154 / 95 – 187 / 85 = – 937 / 1615.
12 48 / 102 ответ 6 – го.
Первое задание : а)1001 – 4230 : 47 = 911 б)16271 : 53 + 18 * 18 = 631.
Каждый диаметр = 6 они равны так как 3•2 = 6.
Вчетверо больше, значит 5 * 4 = 20(столько этажей в доме Бориса). 20 – 5 = 15(На столько этажей дом Бориса выше дома Антона).
2 картофеля дешевле, то стоимость 5 кг моркови больше 5 кг моркови стоит 5 * y 2кг картофеля стоит 2 * x 5 * y – 2 * x – на сколько 2 кг . Картофеля дешевле, чем 5 кг моркои ответ : 5 * y – 2 * x.
Углы, связанные с окружностью
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
| Фигура | Рисунок | Теорема |
| Вписанный угол |  |
|
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  |
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  |
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  |
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
Теоремы об углах, образованных хордами, касательными и секущими
| Вписанный угол |
| Окружность, описанная около прямоугольного треугольника |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |
 |
|
| Угол, образованный секущими, которые пересекаются вне круга |  |
 |
|
| Угол, образованный касательной и хордой, проходящей через точку касания |  |
 |
|
| Угол, образованный касательной и секущей |  |
 |
|
| Угол, образованный двумя касательными к окружности |  |
 |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
|
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
|
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
|
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство [spoiler title=”источники:”] http://matematika.my-dict.ru/q/8066977_vpisannyj-ugol-bac-okruznosti-s-centrom/ http://www.resolventa.ru/spr/planimetry/cangle.htm [/spoiler] |
Skip to content
Home » ЕГЭ » B6 » Геометрия. Планиметрия. Окружность.
Точка O – центр окружности, угол BOC=160°. Найдите величину угла BAC.
Решение:
Угол BOC – центральный угол.
Угол BАC – вписанный угол.
Вписанный угол меньше центрального угла в два раза.
Угол BAC= BOC:2=160:2=80°
Ответ: 80
Видео вебинара, где рассмотрено решение геометрии.
Кликните СЮДА, чтобы посмотреть видео.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Ученик
(232),
закрыт
5 лет назад
Михаил Лебедев
Мудрец
(11387)
5 лет назад
ОВ – радиус. Значит, ОB=OA, но ОА=АВ => OB=OA=AB=R – тр-к равносторонний, т. е. углы равны 60 гр. (180/3).
Касательная С к окружности перпендикулярна к радиусу, проведенному в точку касания A(теорема).
Cледовательно, угол ОАС=90гр. Тогда угол ВАС=угол ОАС-угол OAB=90-60=30гр.
Рассмотрим разновидность задания № (25) — геометрическая задача на вычисление градусной меры угла с помощью окружности.
Обрати внимание!
В данном номере необходимо выполнять дополнительные построения.
Для выполнения необходимо вспомнить теорию.
Пример:
в прямоугольном треугольнике
ABC
с прямым углом
B
проведена биссектриса угла
A
. Известно, что она пересекает серединный перпендикуляр, проведённый к стороне
BC
в точке
K
. Найди угол
BCK
, если известно, что угол
ACB
равен 20(°).
Как решить задание из примера?
Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.
Рис. (1). Чертёж
Дано:
ΔABC
;
∠B=90°
;
∠BAL=∠CAL
; (p) – серединный перпендикуляр к (BC),
AL∩p=K
;
∠ACB=20°
.
Решение
1) Построим прямоугольный треугольник (ABC) с прямым углом (B), проведём биссектрису угла (A)
(
∠ABC=90°;∠BAL=∠LAC,
так как (AL) — биссектриса).
2) Сделаем дополнительное построение: проведём окружность, описанную около треугольника (ABC). Тогда получим, что биссектриса пересекает окружность в точке (L).
Соединим точки, получим треугольник (BCL). Так как
∠BAL=∠CAL
, а (AL) — биссектриса, то дуга (BL) равна дуге (LC). А раз дуги равны, то хорды, стягивающие эти дуги, также будут равны, отсюда следует, что треугольник (BLC) — равнобедренный.
3) Проведём высоту из вершины (L) к основанию (BC). Так как (LN) — это высота, опущенная из вершины равнобедренного треугольника к основанию, то она также является биссектрисой и медианой, тогда (BN=BC). Отсюда следует, что (LN) — серединный перпендикуляр. Это означает, что точка (L) совпадает с точкой (K), то есть с точкой пересечения серединного перпендикуляра к (BC) и биссектрисой.
4)
∠BCK=∠BAK
(точка (L) есть точка (K)) как вписанные углы, опирающиеся на одну и ту же дугу, а
∠BAK=12∠BAC
.
Найдём угол (BAC):
(так как сумма углов треугольника равна (180°));
Значит, угол (BCK) равен 35(°).
Обрати внимание!
Ответ запиши с единицами измерения.
Источники:
Рис. 1. Чертёж. © ЯКласс.
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Центральные и вписанные углы окружности
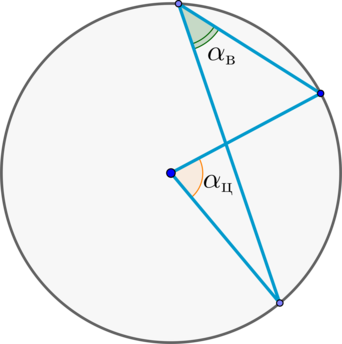
(blacktriangleright) Центральный угол – угол, вершина которого лежит в центре окружности.
Центральный угол равен дуге, на которую он опирается.
(blacktriangleright) Вписанный угол – угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую он опирается.
(blacktriangleright) Таким образом, если центральный угол (alpha_{text{ц}}) и вписанный угол (alpha_{text{в}}) опираются на одну и ту же дугу, то: [Large{alpha_{text{ц}}=2cdot
alpha_{text{в}}}]
(blacktriangleright) Вписанный угол, опирающийся на полуокружность (или на диаметр), равен (90^circ).
Задание
1
#2156
Уровень задания: Равен ЕГЭ
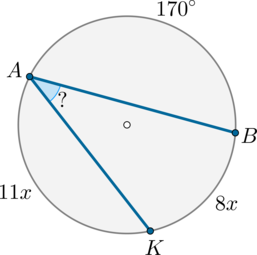
Точки (A) и (B) делят окружность на две дуги, одна из которых равна (170^circ), а другая точкой (K) делится в отношении (11:8), считая от точки (A). Найдите (angle BAK). Ответ дайте в градусах.
Рассмотрим картинку:
Т.к. (buildrelsmileover{AK}:buildrelsmileover{KB}=11:8), то можно обозначить (buildrelsmileover{AK}=11x,
buildrelsmileover{KB}=8x).
Дуга (buildrelsmileover{AKB}=360^circ -170^circ=190^circ). Следовательно, (11x+8x=19x=190^circ quad Rightarrow quad
x=10^circ). Значит, дуга (buildrelsmileover{KB}=8x=80^circ). Угол (BAK) вписанный и опирается на эту дугу, следовательно, он равен ее половине, то есть (40^circ).
Ответ: 40
Задание
2
#2159
Уровень задания: Равен ЕГЭ
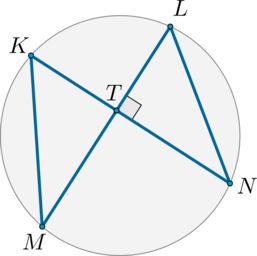
Хорды (KN) и (LM) взаимно перпендикулярны. Найдите угол (NLM), если угол (KML) равен (35^circ). Ответ дайте в градусах.
Рассмотрим картинку:
Вписанные углы (KML) и (KNL) опираются на одну и ту же дугу, следовательно, они равны, значит, (angle KNL=35^circ). Тогда (angle NLM=180^circ-90^circ-35^circ=55^circ).
Ответ: 55
Задание
3
#2155
Уровень задания: Равен ЕГЭ
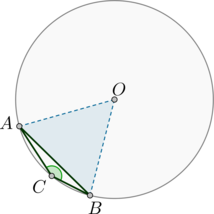
Точки (A) и (C) разбивают окружность на две дуги, одна из которых равна (280^circ) и на которой отмечена точка (B). Найдите угол (BAC), если (AB=AC). Ответ дайте в градусах.
Рассмотрим картинку:
(buildrelsmileover{ABC}=280^circ), следовательно, меньшая дуга (buildrelsmileover{AC}=360^circ-280^circ=80^circ). Т.к. угол (ABC) опирается на эту дугу и является вписанным, то он равен ее половине, то есть (40^circ).
Заметим, что (triangle ABC) – равнобедренный, следовательно, (angle BAC=180^circ-2cdot 40^circ=100^circ).
Ответ: 100
Задание
4
#630
Уровень задания: Равен ЕГЭ
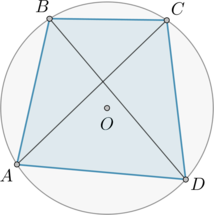
Точки (A), (B), (C) и (D) лежат на окружности с центром в точке (O) (так, что (ABCD) – четырёхугольник). Длина дуги (AD) (которая меньше полуокружности) составляет (0,8) длины дуги (AB) (которая меньше полуокружности). Найдите, во сколько раз (angle AOB) больше, чем (angle DCA).
Градусные меры дуг окружности относятся как их длины, тогда градусная мера дуги (AB) в (1: 0,8 = 1,25) раз больше, чем градусная мера дуги (AD).
Градусной мерой дуги называется градусная мера центрального угла, который на неё опирается.
Вписанный угол равен половине градусной меры дуги, на которую он опирается, тогда [dfrac{angle AOB}{angle DCA} = dfrac{smile AB}{0,5 smile AD} = 2 cdot dfrac{smile AB}{smile AD} = 2,5.]
Ответ: 2,5
Задание
5
#632
Уровень задания: Равен ЕГЭ
Хорды окружности (AB) и (CD) пересекаются в точке (E), причём (CE = AE). Градусная мера дуги (AC) равна (120^{circ}), градусная мера дуги (CAD) равна (210^{circ}). Найдите градусную меру дуги (BD). Ответ дайте в градусах.
Градусная мера дуги (DA) равна (210^{circ} – 120^{circ} = 90^{circ}).
Соединим (CA).
Треугольник (AEC) – равнобедренный, тогда (angle DCA = angle BAC), тогда дуги, на которые опираются эти вписанные углы, равны, следовательно градусная мера дуги (BC) равна (90^{circ}).
Градусная мера дуги (BD) равна (360^{circ} – 120^{circ} – 90^{circ} – 90^{circ} = 60^{circ}).
Ответ: 60
Задание
6
#3531
Уровень задания: Равен ЕГЭ
Четырехугольник (ABCD) вписан в окружность. Угол (ABD) равен (75^circ), угол (CAD) равен (35^circ). Найдите угол (ABC). Ответ дайте в градусах.
Так как вписанный угол равен половине дуги, на которую он опирается, то меньшая (buildrelsmileover{DA},=2cdot 75^circ=150^circ) (см.рис.). Аналогично меньшая дуга (buildrelsmileover{CD},=2cdot 35^circ=70^circ) (см.рис.). Следовательно, дуга (buildrelsmileover{CDA},=150^circ+70^circ=220^circ). Значит (angle ABC), как вписанный и опирающийся на дугу, равную (220^circ), сам равен (110^circ).
Ответ: 110
Задание
7
#3523
Уровень задания: Равен ЕГЭ
Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Обозначим хорду за (AB). Рассмотрим (triangle AOB), где (O) – центр окружности.
Так как (AB) равна радиусу окружности, то (triangle AOB) – равносторонний. Следовательно, (angle AOB=60^circ).
Следовательно, меньшая дуга (AB) окружности равна (angle
AOB=60^circ). Тогда большая дуга (AB) окружности равна (360^circ-60^circ=300^circ). Заметим, что (angle ACB) – вписанный угол, опирающийся на большую дугу (AB), следовательно, он равен ее половине, то есть (angle ACB=150^circ).
Ответ: 150
Чаще всего процесс подготовки к ЕГЭ по математике начинается с повторения основных определений, формул и теорем, в том числе и по теме «Центральный и вписанный в окружность угол». Как правило, данный раздел планиметрии изучается еще в средней школе. Неудивительно, что многие учащиеся сталкиваются с необходимостью повторения базовых понятий и теорем по теме «Центральный угол окружности». Разобравшись с алгоритмом решения подобных задач, школьники смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена.
Как легко и эффективно подготовиться к прохождению аттестационного испытания?
Занимаясь перед сдачей единого государственного экзамена, многие старшеклассники сталкиваются с проблемой поиска нужной информации по теме «Центральный и вписанный углы в окружности». Далеко не всегда школьный учебник имеется под рукой. А поиск формул в Интернете порой отнимает очень много времени.
«Прокачать» навыки и улучшить знания в таком непростом разделе геометрии, как планиметрия, вам поможет наш образовательный портал. «Школково» предлагает старшеклассникам и их преподавателям по-новому выстроить процесс подготовки к сдаче единого госэкзамена. Весь базовый материал представлен нашими специалистами в максимально доступной форме. Ознакомившись с информацией в разделе «Теоретическая справка», учащиеся узнают, какими свойствами обладает центральный угол окружности, как найти его величину и т. д.
Затем для закрепления полученных знаний и отработки навыков мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий на нахождение величины угла, вписанного в окружность, внешних углов многоугольника и других параметров представлена в разделе «Каталог». Для каждого упражнения наши специалисты прописали подробный ход решения и указали правильный ответ. Перечень задач на сайте постоянно дополняется и обновляется.
Готовиться к ЕГЭ, практикуясь в выполнении упражнений, к примеру, на нахождение величины центрального угла и длины дуги окружности, старшеклассники могут в онлайн-режиме, находясь в любом российском регионе.
При необходимости выполненное задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и еще раз разобрать принцип его решения.

УСТАЛ? Просто отдохни