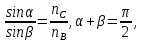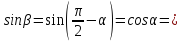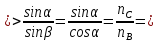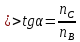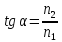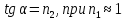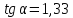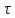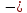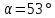Федеральное
агентство связи
СибГУТИ
Кафедра
физики
Лабораторная
работа № 7.6
«ИССЛЕДОВАНИЕ
ПОЛЯРИЗАЦИИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН, ПРИ
ИХ ОТРАЖЕНИИ ОТ ДИЭЛЕКТРИКА»
Выполнил:
студент гр. ИС-74*
Некто
Н.Н.
Преподаватель:
Лубский
В. В.
Выполнение:
21.02.2018 _
________________
дата подпись
Защита:
_______________ _
________________
оценка дата подпись
Новосибирск
2018 г.
1)
Цель работы
Определить
угол Брюстера. На основе экспериментальных
данных рассчитать абсолютный показатель
преломления стекла.
2)
Краткая теория
Пусть
на границу раздела двух диэлектриков
падает под углом α, не равным нулю,
естественный свет, то отраженная и
преломленная световая волна будут
частично поляризованы. Векторы
напряженности световой волны можно
разложить по базису: компонент
перпендикулярной и параллельной
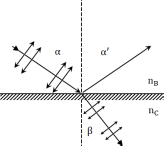
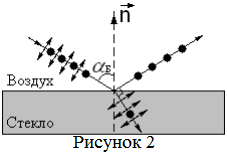
плоскости падения. На рис.1 изображены
параллельные (стрелками) и перпендикулярные
(точками) составляющие векторов
напряженности электрического поля. Е0
для падающей волны, Е1 для отраженной,
Е2 для преломленной.
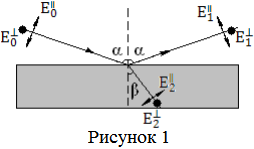
Значения
этих величин следуют из условий на
границе раздела двух сред для электрического
и магнитного полей световой волны.
Формулы, выражающие параллельные и
перпендикулярные компоненты амплитуды
вектора Е преломленной и отраженной
волны, через соответствующие компоненты
падающей названы формулами Френеля:
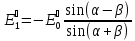 (1)
(1) 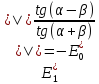 (2)
(2)
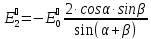 (3)
(3) 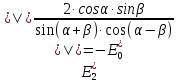 (4)
(4)
Так
как интенсивность пропорциональна
квадрату амплитуды (I
~ E2)
и в естественном (неполяризованном)
свете все направления колебаний
электрического поля равновероятны,
тогда естественный свет можно представить
как сумму двух линейно поляризованных
волн равной интенсивности, в которых
колебания происходят соответственно
параллельно и перпендикулярно плоскости
падения.
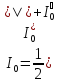
(5)
Выражения
для интенсивностей можно записать в
виде:
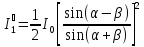 (6)
(6) 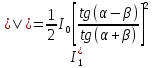 (7)
(7)
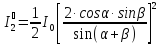 (8)
(8) 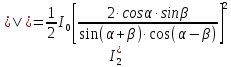 (9)
(9)
В
основе механизма поляризации лежит
взаимодействие электромагнитной волны
с валентными электронами диэлектрика.
![]()
Для
некоторого угла падения для которого
выполняется соотношение параллельная
составляющая интенсивности отраженного
луча равна нулю. Используя закон
преломления можно связать с показателями
преломления сред. Брюстером впервые
было показано, что степень поляризации
обеих волн, при условии:
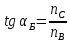
(10)
,
где nB
– абсолютный показатель преломления
той среды, из которой проходит
электромагнитная волна, nС
– абсолютный показатель преломления
диэлектрика. Величина
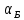 ,
,
входящая в закон Брюстера (10), носит
название «Угол Брюстера».
Экспериментальное
определение величины
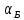
и расчет значения nC
составляют основное содержание данной
лабораторной работы. В условиях
проводимого эксперимента, электромагнитная
волна падает на диэлектрик из воздуха,
для которого среднее значение абсолютного
показателя преломления (для электромагнитных
волн видимого диапазона – 380
760 нм) составляет величину nВ
= 1,000292. В пределах точности эксперимента,
можно принять значение nВ
≈ 1. В качестве диэлектрика используется
набор плоско- параллельных стеклянных
пластин с абсолютным показателем
преломления nС,
вплотную прижатых одна к другой. Такое
устройство обычно называют стеклянной
стопой. С учетом сказанного, формула
(1) преобразуется к виду:
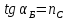
(11)
3)
Описание лабораторной установки
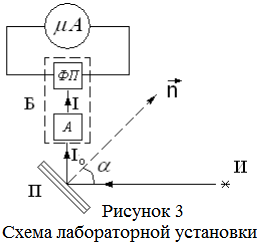
Принципиальная
схема установки показана на рис. 3.
Электромагнитная волна от источника
«И» падает на стеклянную стопу «П» и
отражается от неё, поляризуясь. Для
анализа отражённого поляризованного
излучения используется поляроид «А»,
представляющий собой плёнку поливинилена
толщиной 0,5 мм. Пройдя через поляроид
«А», электромагнитная волна падает на
поверхность фотоприёмника, в качестве
которого используется кремневый фотодиод
«ФП». К фотоприёмнику подключен
микроамперметр «µА», который служит
для регистрации тока, возникающего в
цепи, под воздействием на фотоприёмник
поляризованной электромагнитной волны.
Поляроид «А» и фотоприёмник «ФП»
объединены в один блок «Б», способный
поворачиваться в вертикальной плоскости
вокруг горизонтальной оси.
Стеклянная
стопа «П» закреплена на вращающейся
платформе горизонтально расположенного
гониометра – прибора, предназначенного
для отсчёта углов падения волн
. Как и блок «Б», стопа «П» может вращаться
вокруг вертикальной оси. Стопа «П» в
данном эксперименте выполняет функцию
поляризатора электромагнитного
излучения, поляроид «А» служит
анализатором.
4)
Выполнение
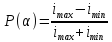
Таблица
№1
|
|
imax, |
imin, |
P(α) |
|
30 |
39,5 |
36 |
0,046 |
|
35 |
40 |
33 |
0,096 |
|
40 |
42 |
29 |
0,183 |
|
45 |
43,5 |
25,5 |
0,261 |
|
50 |
47 |
23 |
0,343 |
|
52,5 |
48,5 |
22 |
0,376 |
|
55 |
50,5 |
22 |
0,393 |
|
57,5 |
54 |
23,5 |
0,394 |
Продолжение
таблицы №1
|
60 |
56 |
26 |
0,366 |
|
65 |
68 |
40 |
0,259 |
|
70 |
82,5 |
62,5 |
0,138 |
График
зависимости P(α):
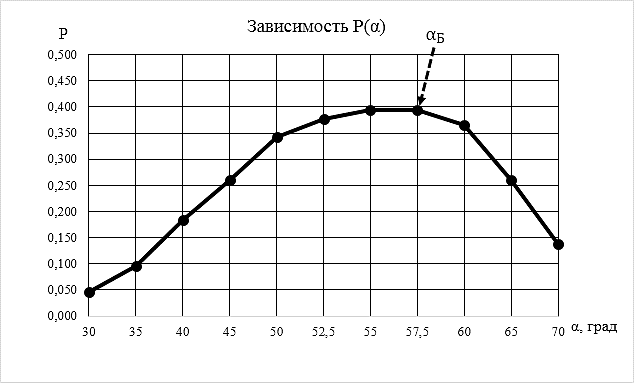
Так
как nВ
≈ 1, то
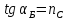
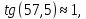 5697
5697
Тип
среды: оптические стёкла, среда Ф1 (Флинт)
= 1,6128
Абсолютная
погрешность:
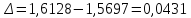
Относительная
погрешность:
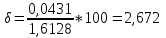
Вывод:
подводя соответствующие измерения и
построив график зависимости P(α), я
выяснил, что угол Брюстера равен 57,5°.
Также,
я вычислил абсолютный показатель
преломления стекла (nC
= 1,5697) и относительную погрешность
измерения (δ = 2,672 %).
5)
Ответы на контрольные вопросы
1)
Дайте понятие поляризации электромагнитных
волн.
I)
Поляризация магнитных волн – явление
направленного колебания векторов
напряжённости электрического поля E
или напряжённости магнитного поля H.
2)
В чём сущность закона Брюстера?
II)
Закон Брюстера – соотношение между
показателем преломления диэлектрика
nC,
показателем преломления среды nB
и углом падения естественного света,
при котором свет, отражённый от поверхности
диэлектрика, полностью поляризуется:
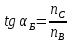
Получение
полной линейной поляризации при отражении
света от границы раздела двух диэлектриков
называют явлением Брюстера. Оно
реализуется тогда и только тогда, когда
угол между отраженной и преломленной
волнами равен
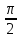 .
.
3)
Каково назначение поляризатора и
анализатора в данной работе?
III)
Поляризатор – прибор, преобразующий
естественный свет в полностью или (реже)
частично поляризованный.
Анализатор
– устройство, предназначенное для
определения степени поляризации света
или для регистрации её изменений.
Электромагнитная
волна от источника падает на поляризатор
и отражается от неё, поляризуясь. Для
анализа отраженного поляризованного
излучения используется анализатор,
представляющий собой плёнку поливинилена
толщиной 0,5 мм. Пройдя через анализатор,
электромагнитная волна падает на
поверхность фотоприемника, в качестве
которого используется кремневый
фотодиод. К фотоприемнику подключен
микроамперметр, который служит для
регистрации тока, возникающего в цепи,
под воздействием на фотоприёмник
поляризованной электромагнитной волны.
4)
Какие величины связывают формулы
Френеля? Для какого света они применимы?
IV)
Формулы Френеля связывают
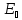
и
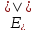 ,
,
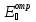
и
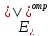 ,
,
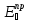
и
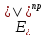 .
.
Формулы
Френеля применимы для естественного,
неполяризованного света.
5)
Дайте качественное объяснение механизма
поляризации электромагнитной волны
при её взаимодействии с диэлектриком.
V)
В основе механизма поляризации лежит
взаимодействие электромагнитной волны
с валентными электронами диэлектрика.
Падающая
волна, проникнув в диэлектрик, заставляет
входящие в состав атомов электрические
заряды совершать вынужденные колебания.
Колеблющиеся заряды излучают вторичные
электромагнитные волны. не диэлектрика,
вторичные волны, налагаясь друг на
друга, дают отражённую волну. Внутри
диэлектрика вторичные волны складываются
с первичной волной. Результирующая
первичной и вторичной волн даёт
преломленную волну. Вынужденные колебания
зарядов совершаются в направлении
вектора E
этой результирующей волны.
6)
Сделать вывод рабочей формулы tg
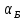 =
=
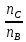 .
.
VI)
|
|
|
7)
Почему для угла Брюстера справедливо
выражение
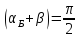 .
.
VII)
Рассмотрим одну из формул Френеля:
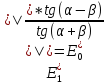
Известно,
что при явлении Брюстера угол α + β равен
90°.

Подставим
полученное значение в исходную формулу:
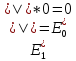
Вывод:
для некоторого угла падения
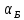 ,
,
для которого выполняется соотношение
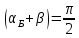 ,
,
параллельная составляющая интенсивности
отражённого луча равна нулю.
6)
Решение задач:
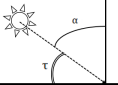
2.2.
Под каким углом к горизонту должно
находиться Солнце, чтобы его
лучи,
отраженные от поверхности озера были
полностью поляризованы? Показатель
преломления воды равен 1.33.
Дано: Решение:
|
n1 n2 |
|
|
|
|
|
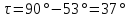
Ответ:
τ = 37°.
Соседние файлы в предмете Физика
- #
- #
- #
- #
From Wikipedia, the free encyclopedia

An illustration of the polarization of light that is incident on an interface at Brewster’s angle.
Brewster’s angle (also known as the polarization angle) is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly polarized. This special angle of incidence is named after the Scottish physicist Sir David Brewster (1781–1868).[1][2]
Explanation[edit]
When light encounters a boundary between two media with different refractive indices, some of it is usually reflected as shown in the figure above. The fraction that is reflected is described by the Fresnel equations, and depends on the incoming light’s polarization and angle of incidence.
The Fresnel equations predict that light with the p polarization (electric field polarized in the same plane as the incident ray and the surface normal at the point of incidence) will not be reflected if the angle of incidence is
where n1 is the refractive index of the initial medium through which the light propagates (the “incident medium”), and n2 is the index of the other medium. This equation is known as Brewster’s law, and the angle defined by it is Brewster’s angle.
The physical mechanism for this can be qualitatively understood from the manner in which electric dipoles in the media respond to p-polarized light. One can imagine that light incident on the surface is absorbed, and then re-radiated by oscillating electric dipoles at the interface between the two media. The polarization of freely propagating light is always perpendicular to the direction in which the light is travelling. The dipoles that produce the transmitted (refracted) light oscillate in the polarization direction of that light. These same oscillating dipoles also generate the reflected light. However, dipoles do not radiate any energy in the direction of the dipole moment. If the refracted light is p-polarized and propagates exactly perpendicular to the direction in which the light is predicted to be specularly reflected, the dipoles point along the specular reflection direction and therefore no light can be reflected. (See diagram, above)
With simple geometry this condition can be expressed as
where θ1 is the angle of reflection (or incidence) and θ2 is the angle of refraction.
Using Snell’s law,
one can calculate the incident angle θ1 = θB at which no light is reflected:
Solving for θB gives
For a glass medium (n2 ≈ 1.5) in air (n1 ≈ 1), Brewster’s angle for visible light is approximately 56°, while for an air-water interface (n2 ≈ 1.33), it is approximately 53°. Since the refractive index for a given medium changes depending on the wavelength of light, Brewster’s angle will also vary with wavelength.
The phenomenon of light being polarized by reflection from a surface at a particular angle was first observed by Étienne-Louis Malus in 1808.[3] He attempted to relate the polarizing angle to the refractive index of the material, but was frustrated by the inconsistent quality of glasses available at that time. In 1815, Brewster experimented with higher-quality materials and showed that this angle was a function of the refractive index, defining Brewster’s law.
Brewster’s angle is often referred to as the “polarizing angle”, because light that reflects from a surface at this angle is entirely polarized perpendicular to the plane of incidence (“s-polarized”). A glass plate or a stack of plates placed at Brewster’s angle in a light beam can, thus, be used as a polarizer. The concept of a polarizing angle can be extended to the concept of a Brewster wavenumber to cover planar interfaces between two linear bianisotropic materials. In the case of reflection at Brewster’s angle, the reflected and refracted rays are mutually perpendicular.
For magnetic materials, Brewster’s angle can exist for only one of the incident wave polarizations, as determined by the relative strengths of the dielectric permittivity and magnetic permeability.[4] This has implications for the existence of generalized Brewster angles for dielectric metasurfaces.[5]
Applications[edit]
While at the Brewster angle there is no reflection of the p polarization, at yet greater angles the reflection coefficient of the p polarization is always less than that of the s polarization, almost up to 90° incidence where the reflectivity of each rises towards unity. Thus reflected light from horizontal surfaces (such as the surface of a road) at a distance much greater than ones height (so that the incidence angle of specularly reflected light is near, or usually well beyond the Brewster angle) is strongly s-polarized. Polarized sunglasses use a sheet of polarizing material to block horizontally-polarized light and thus reduce glare in such situations. These are most effective with smooth surfaces where specular reflection (thus from light whose angle of incidence is the same as the angle of reflection defined by the angle observed from) is dominant, but even diffuse reflections from roads for instance, are also significantly reduced.
Photographers also use polarizing filters to remove reflections from water so that they can photograph objects beneath the surface. Using a polarizing camera attachment which can be rotated, such a filter can be adjusted to reduce reflections from objects other than horizontal surfaces, such as seen in the accompanying photograph (right) where the s polarization (approximately vertical) has been eliminated using such a filter.

Photographs taken of a window with a camera polarizer filter rotated to two different angles. In the picture at left, the polarizer is aligned to pass only the vertical polarization which is strongly reflected from the window. In the picture at right, the polarizer has been rotated 90° to eliminate the heavily polarized reflected sunlight, passing only the p (horizontal in this case) polarization.
When recording a classical hologram, the bright reference beam is typically arranged to strike the film in the p polarization at Brewster’s angle. By thus eliminating reflection of the reference beam at the transparent back surface of the holographic film, unwanted interference effects in the resulting hologram are avoided.
Entrance windows or prisms with their surfaces at the Brewster angle are commonly used in optics and laser physics in particular. The polarized laser light enters the prism at Brewster’s angle without any reflective losses.
In surface science, Brewster angle microscopes are used to image layers of particles or molecules at air-liquid interfaces. Using illumination by a laser at Brewster’s angle to the interface and observation at the angle of reflection, the uniform liquid does not reflect, appearing black in the image. However any molecular layers or artifacts at the surface, whose refractive index or physical structure contrasts with the liquid, allows for some reflection against that black background which is captured by a camera.
Brewster windows[edit]

Gas lasers using an external cavity (reflection by one or both mirrors outside the gain medium) generally seal the tube using windows tilted at Brewster’s angle. This prevents light in the intended polarization from being lost through reflection (and reducing the round-trip gain of the laser) which is critical in lasers having a low round-trip gain. On the other hand it does remove s polarized light, increasing the round trip loss for that polarization, and ensuring the laser only oscillates in one linear polarization, as is usually desired. And many sealed-tube lasers (which don’t even need windows) have a glass plate inserted within the tube at the Brewster angle, simply for the purpose of allowing lasing in only one polarization.[6]
Pseudo-Brewster’s angle [edit]
When the reflecting surface is absorbing, reflectivity at parallel polarization (p) goes through a non-zero minimum at the so-called pseudo-Brewster’s angle.[7][8]
See also[edit]
- Brewster angle microscope
- Critical angle, the angle of total internal reflection.
References[edit]
- ^ Brewster, David (1815). “On the laws which regulate the polarisation of light by reflexion from transparent bodies”. Philosophical Transactions of the Royal Society of London. 105: 125–159. doi:10.1098/rstl.1815.0010.
- ^ Lakhtakia, Akhlesh (June 1989). “Would Brewster recognize today’s Brewster angle?” (PDF). Optics News. 15 (6): 14–18. doi:10.1364/ON.15.6.000014.
- ^ See:
- Malus (1809) “Sur une propriété de la lumière réfléchie” (On a property of reflected light), Mémoires de physique et de chimie de la Société d’Arcueil, 2 : 143–158.
- Malus, E.L. (1809) “Sur une propriété de la lumière réfléchie par les corps diaphanes” (On a property of light reflected by translucent substances), Nouveau Bulletin des Sciences [par la Societé Philomatique de Paris], 1 : 266–270.
- Etienne Louis Malus, Théorie de la double réfraction de la lumière dans les substances cristallisées [Theory of the double refraction of light in crystallized substances] (Paris, France: Garnery, 1810), Chapitre troisième. Des nouvelles propriétés physiques que la lumière acquiert par l’influence des corps qui la réfractent ou la réfléchissent. (Chapter 3. On new physical properties that light acquires by the influence of bodies that refract it or reflect it.), pp. 413–449.
- ^ Giles, C. L.; Wild, W. J. (1985). “Brewster angles for magnetic media” (PDF). International Journal of Infrared and Millimeter Waves. 6 (3): 187–197. Bibcode:1985IJIMW…6..187G. doi:10.1007/BF01010357. S2CID 122287937. Archived (PDF) from the original on 9 October 2022.
- ^ Paniagua-Domínguez, Ramón; Feng Yu, Ye; Miroshnichenko, Andrey E.; Krivitsky, Leonid A.; Fu, Yuan Hsing; Valuckas, Vytautas; Gonzaga, Leonard; et al. (2016). “Generalized Brewster effect in dielectric metasurfaces”. Nature Communications. 7: 10362. arXiv:1506.08267. Bibcode:2016NatCo…710362P. doi:10.1038/ncomms10362. PMC 4735648. PMID 26783075.
- ^ Optics, 3rd edition, Hecht, ISBN 0-201-30425-2
- ^ Azzam, Rasheed M A (14 September 1994). Goldstein, Dennis H; Chenault, David B (eds.). “Fresnel’s interface reflection coefficients for the parallel and perpendicular polarizations: global properties and facts not found in your textbook”. Proc. SPIE. Polarization Analysis and Measurement II. 2265: 120. Bibcode:1994SPIE.2265..120A. doi:10.1117/12.186660. S2CID 135659948.
- ^ Barclay, Les, ed. (2003). Propagation of Radiowaves. Electromagnetics and Radar. Vol. 2 (2nd ed.). IET. p. 96. ISBN 9780852961025.
Further reading[edit]
- Lakhtakia, A. (1992). “General schema for the Brewster conditions” (PDF). Optik. 90 (4): 184–186.
External links[edit]
- Brewster’s Angle Extraction from Wolfram Research
- Brewster window at RP-photonics.com
- TE, TM Reflection Coefficients – interactive phase and magnitude plots showing Brewster’s angle
Угол Брюстера
Содержание:
-
Что такое угол Брюстера и формула расчета
- Чему равен угол Брюстера для стекла, погруженного в воду
-
Отражение под углом Брюстера
- Угол Брюстера — полное преломление
Что такое угол Брюстера и формула расчета
Определение
Явление Брюстера — полная линейная поляризация при отражении света от границы двух прозрачных диэлектриков. Возможно только в том случае, когда угол между отраженным и преломленным лучами — (frac{mathrmpi}2).
Определение
Закон Брюстера: тангенс угла полной поляризации, известного теперь, как угол Брюстера, равен показателю преломления вещества.
(tan{left(alpharight)}_{Бр};=;frac{n_2}{n_1}.)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Явление Брюстера вызвано поперечностью электромагнитной волны. Под влиянием падающей волны электроны вещества совершают колебания и излучают вторичные волны, которые накладываются на первоначальные колебания. На длине смещения происходит полная замена падающей волны волной, которую излучают электроны при своих колебаниях.
Чему равен угол Брюстера для стекла, погруженного в воду
Коэффициент преломления света в веществе равен отношению скорости света в вакууме к скорости света в этом веществе. Для воды значение этого показателя равно 1,33, для стекла — 1,52. Следовательно, преобразовав формулу закона Брюстера в формулу для расчета угла, получим:
(alpha_{Бр};=arctanleft(;frac{n_2}{n_1}right);=;41,19^circ.)
Отражение под углом Брюстера
Отраженный под углом Брюстера луч полностью поляризован и всегда расположен под углом 90 градусов к преломленному лучу. Каждая точка поверхности, куда попадает волна, становится вторичным источником лучей — она провоцирует совместные осцилляции дипольных моментов молекул диэлектрика.
Новые волны, попадая в свободное пространство, при движении вперед создают отраженную и преломленную волну.
Под другим углом граница раздела сред не может отразить 100 процентов света, часть его входит в состав преломленного луча, так что полная поляризация недостижима. Интенсивность отраженного поляризованного луча при использовании одной пластинки крайне мала — например, для границы воздуха и стекла она составляет около 4% от первоначального луча. Можно сделать интенсивность больше — для этого используют специальное приспособление, стопу Столетова. Оно представляет собой несколько соединенных пластинок.
Угол Брюстера — полное преломление
Определение
Полное преломление — явление, возникающее при падении поперечных волн на границу раздела однородных сред и отсутствии отраженных лучей. Это явление также называют полным внутренним отражением света.
Явление полного преломления возможно только при падении на границу сред вертикально поляризованной волны под углом Брюстера. Закон преломления подразумевает, что в отраженном потоке могут оказаться лишь горизонтально поляризованные волны. Но если в падающей волне горизонтально поляризованные элементы отсутствовали, отражение тоже будет отсутствовать.
Насколько полезной была для вас статья?
Рейтинг: 2.63 (Голосов: 8)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Соотношение фаз в падающей и преломленной (отраженной) волнах
Используя формулы Френеля:
можно найти фазовые соотношения между отраженной (преломленной) и падающей волнами. Углы падения и преломления всегда находятся в пределах от $0$ до $900$. Следовательно, при любых значениях $alpha и {alpha }_{pr}$, как следует из (1) $E_{pr//} и $ $E_{prbot }$ совпадают по знаку с соответствующими им составляющими ${E_{pad//},E}_{padbot }$. Это означает, что на границе раздела веществ фаза волны преломления совпадает с фазой падающей волны.
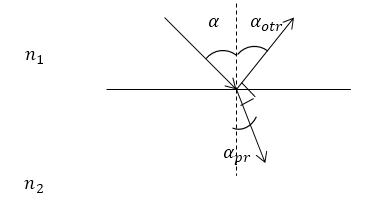
Рисунок 1.
Рассмотрим отраженную волну. Ее составляющая ($E_{otr//}$) совпадает по знаку в соответствующем выражении системы (1) в том случае, если: ${tg left(alpha -{alpha }_{pr}right) } >0 и tg(alpha +{alpha }_{pr}) >0$ или ${tg left(alpha -{alpha }_{pr}right) }
-
при $alpha >{alpha }_{pr}$ ($n_{21} >1$) и $alpha +{alpha }_{pr}
-
при $alpha frac{pi }{2}$.
Данное отражение составляющей $E_{pad//}$ сопровождается сдвигом по фазе на $pi $. Отражение параллельной составляющей без сдвига фаз происходит в случаях:
-
при $alpha >{alpha }_{pr}$ ($n_{21} >1$) и $alpha +{alpha }_{pr} >frac{pi }{2}$;
-
при $alpha
Для отраженной составляющей волны $E_{otrbot }$ и $E_{padbot }$ совпадают по знаку, и отражение идет без сдвига фаз, в том случае, если $alpha
Явление Брюстера
Угол падения, при котором сумма углов падения и преломления равна $frac{pi }{2}$, называют углом Брюстера (${alpha }_b$). Используя закон преломления для угла Брюстера:
Если угол падения равен углу Брюстера, то между направлениями отраженной и преломленной плоских волн равен $frac{pi }{2}$. Следовательно, ${alpha }_{pr}+alpha frac{pi}{2}$ при $alpha >{alpha }_b$.
«Угол Брюстера» 👇
Отражение света при $alpha 1$) ведет к изменению фаз на $pi $(то есть происходит потеря половины волны).
Если свет на границу раздела двух сред падает под углом Брюстера ($alpha ={alpha }_b,$ то $tgleft({alpha }_b+{alpha }_{pr}right)=infty $) в соответствии с системой (1) $E_{otr//}=0$. Это означает, что в отраженном свете колебания вектора напряженности электрического поля происходят только в плоскости, которая перпендикулярна плоскости падения. То есть отраженный свет является полностью линейно поляризованным. Такой результат отражает смысл закона Брюстера.
Замечание 1
Надо отметить, что при $n_{12}
Отражение под углом Брюстера – один из способов получения линейно поляризованного света.
Явление Брюстера вызвано поперечностью электромагнитной волны. Под влиянием падающей волны электроны вещества совершают колебания и излучают вторичные волны, которые накладываются на первоначальные колебания. На длине смещения происходит полная замена падающей волны волной, которую излучают электроны при своих колебаниях. Линия колебаний электронов коллинеарна вектору $overrightarrow{E}$ волны. При равенстве угла падения углу Брюстера, когда угол между преломленной и отраженной волнами составляет $90^circ$, электроны среды, порождающие преломленную волну, совершают колебания вдоль линии, которая параллельна направлению, в котором должна распространяться отраженная волна. Вдоль линии своих колебаний электрон не может излучать электромагнитную волну. В результате отраженная волна отсутствует.
Исследование процесса отражения света под углами близкими к углу Брюстера дает возможность экспериментально проверить формулы Френеля. Так как интенсивность отраженной под углом Брюстера волны, в которой вектор колеблется в плоскости падения, равна нулю. Данное утверждение удобно для эмпирической проверки, так как при этом не требуется точного соблюдения угла падения. Можно просто непрерывно изменять угол падения около угла Брюстера. При прохождении угла Брюстера интенсивность волны с соответствующей поляризацией обращается в ноль.
Пример 1
Задание: Какова скорость света в кристалле каменной соли, если угол Брюстера при падении пучка света из воздуха составляет ${alpha }_b=57^circ$?
Решение:
В качестве основы для решения задачи используем закон Брюстера:
[{tg(alpha }_b)=frac{n_2}{n_1}left(1.1right).]
Выразим абсолютный показатель преломления кристалла каменной соли из выражения (1.1), имеем:
[n_2=n_1{tg(alpha }_b)left(1.2right).]
Показатель преломления света в кристалле связан со скоростью распространения света в нем как:
[n_2=frac{c}{v_2}left(1.3right),]
где $c$ — скорость света в вакууме. Приравняем правые части выражений (1.2) и (1.3), получим:
[n_1{tg(alpha }_b)=frac{c}{v_2}left(1.4right).]
Выразим из (1.4) искомую скорость ($v_2$), получим:
[v_2=frac{с}{n_1{tg(alpha}_b)}.]
Проведем вычисления, зная, что для воздуха $n_1=1,c=3cdot {10}^8frac{м}{с} $:
[v_2=frac{3cdot {10}^8}{tg(57{}^circ )}=1,94cdot {10}^8(frac{м}{с}).]
Ответ: $v_2=1,94cdot {10}^8frac{м}{с}$.
Пример 2
Задание: Каков двугранный угол стеклянной призмы $theta ,$ на который падает пучок естественный света, если отраженный свет максимально поляризован. Показатель преломления вещества призмы равен $n$.
Решение:
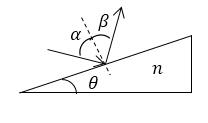
Рисунок 2.
В качестве основы для решения задачи используем закон Брюстера:
[{tg(alpha }_b)=frac{n_2}{n_1}left(2.1right).]
Из выражения (2.1) выразим угол падения:
[{alpha }_b=arctgleft(frac{n_2}{n_1}right)left(2.2right).]
Из рис. 2 видно, что искомый угол равен:
[theta =frac{pi }{2}-{alpha }_b=frac{pi }{2}-arctgleft(frac{n_2}{n_1}right).]
Если пучок света первоначально распространяется в воздухе, то $n_1=1,$ по условию $n_2=n.$
Ответ: $theta =frac{pi }{2}-arctgleft(frac{n_2}{n_1}right).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
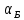 ,
,