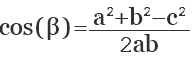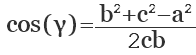Как найти угол диагонали треугольника

Прямоугольник – плоская четырёхугольная геометрическая фигура. Прямоугольник относится к
параллелограммам и обладает некоторыми свойствами:

• Все внутренние углы фигуры прямые.
• Противолежащие стороны попарно параллельны и равны.
• Диагонали прямоугольника (отрезок, соединяющий вершины противоположных внутренних углов) равны.
  Точка пересечения делит их на равные отрезки.
• Диагональ делит фигуру на 2 одинаковых прямоугольных треугольника.
• Диагональ делит внутренний угол (90°) на 2 угла. Накрест лежащие углы при проведенном отрезке
  равны.

Острый угол между диагоналями прямоугольника через площадь и диагональ

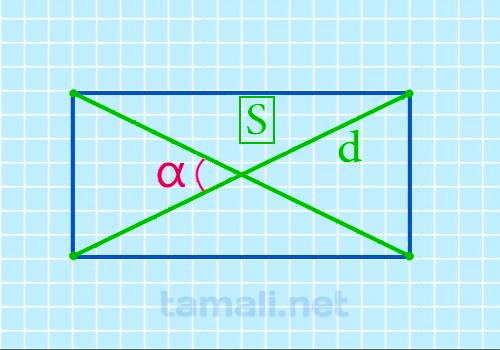
Острый угол (a) между диагоналями, зная площадь (S) и длину диагонали (d) легко можно вычислить по
формуле:

sin a = (2 * S) / d²

где d — диагональ, S — площадь прямоугольника.

Через синус находится значение угла. По этой формуле также можно найти тупой угол между диагоналями,
так как 2 данных угла являются смежными, а синусы смежных углов равны.

Пример. Дан прямоугольник, площадь которого равна 108 см², а диагональ – 15 см.
Нужно найти острый угол между диагоналями. Необходимые значения подставляем в формулу sin a = (2 * S) / d² = (2 * 108) / 225 = 0,96. По значению синуса
находится величина острого угла между диагоналями. В данном случае она равна 73,73°.

Угол между диагоналями прямоугольника через угол между стороной и диагональю

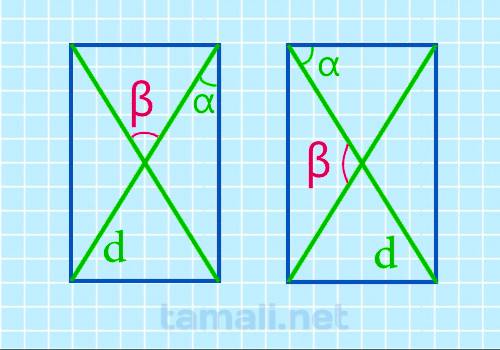
Величина нужного угла (α) в два раза больше угла (β) между стороной и диагональю по свойству углов
равнобедренного треугольника, так как диагонали при пересечении образуют 4 равнобедренных
треугольника. В равнобедренном треугольнике углы при основании (b) равны, а нужный угол является
смежным по отношению к углу при вершине (c), в таком случае c = 180 — α. Сумма углов
треугольника равна 180°. Несложно составить уравнение β+β+180-α=180, которое легко сокращается до
вида

β = 2 * α

где α — угол между стороной и диагональю.

Пример. Пусть угол α = 15 (он может быть от 0 до 90º), тогда β = 2 * α = 2 * 15 = 30º

Острый угол между диагоналями прямоугольника через длину и ширину

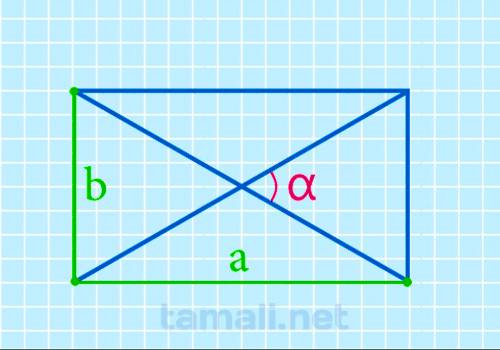
Если в задаче неизвестна длина диагонали, не нужно тратить время на ее поиски. Можно быстро найти
острый угол между диагоналями при помощи длины и ширины прямоугольника по формуле:

α = 2 arctg b / a

где b — ширина прямоугольника, a — длина прямоугольника.

Пример. Дан прямоугольник со сторонами 8 см и 6 см. Нужно построить диагонали и
найти острый угол между ними. Угол α = 2 arctg 6 / 8 = 2 arctg 0,75=73,73°.

Острый угол между диагоналями прямоугольника через ширину и диагональ

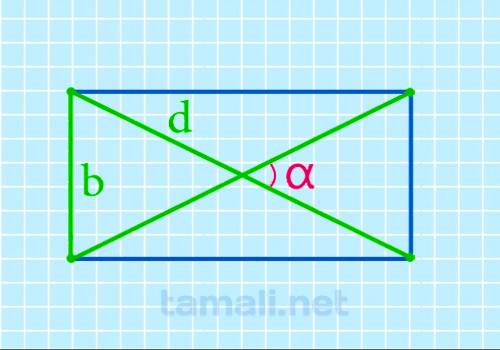
Значение нужного угла можно определить, зная длину диагонали и ширины (B) четырёхугольника, по
формуле:

α = 2 arcsin b / d

где b — ширина прямоугольника, d — диагональ.

Пример. Рассмотрим применение формулы в конкретной задаче. Дан прямоугольник, ширина
которого равна 3 мм, а длина диагонали – 5 мм. Необходимо найти острый угол между
диагоналями. Применив данную формулу, находим значение нужного угла: a = 2 * arcsin 0,6 = 73,73°.

Острый угол между диагоналями прямоугольника через длину и диагональ

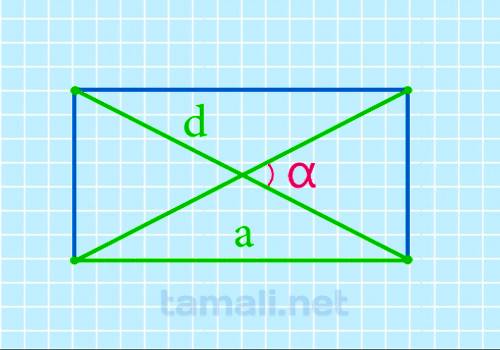
Если неизвестна ширина прямоугольника, но есть значение длины (a), можно также просто найти острый
угол между диагоналями. Формула почти идентична предыдущей:

α = 2 arccos a / d

где a — длина прямоугольника, d — диагональ.

Пример. В прямоугольнике с длиной 8 см, в котором проведены диагонали длиной 10 см,
найти острый угол между диагоналями. Угол α = 2arccos 8 / 10 = 2arccos 0,8 = 73,73°.

Тупой угол между диагоналями прямоугольника через ширину и диагональ

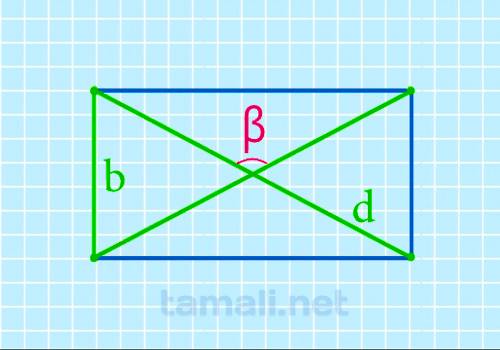
Для того чтобы быстро вычислить значение данного угла при помощи известной ширины и диагонали
прямоугольника, нужно воспользоваться следующей формулой:

β = 2 arccos b / d

где b — ширина прямоугольника, d — диагональ.

Пример. Известна ширина прямоугольника, она равна 8 мм. А длина диагонали равна 17
мм. Задача найти значение тупого угла между диагоналями.
Вставив данные в формулу, вы получите
правильный результат. Таким образом, β = 2 arccos 8 / 17 = 2 arccos 0,47 = 123,85°.

Тупой угол между диагоналями прямоугольника через длину и диагональ

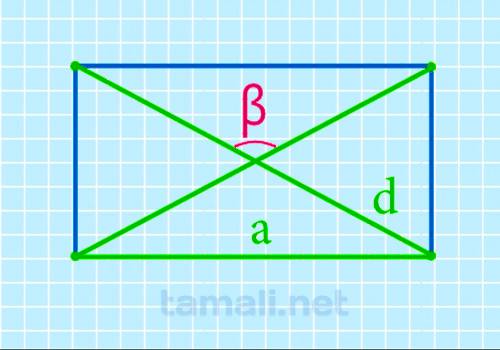
Можно, конечно, применить предыдущую формулу и найти острый угол через длину и диагональ, а потом
вычесть значение из 180°. Но есть упрощенная формула для быстрой скорости решения: тупой угол между
диагоналями

β = 2 arcsin a / d

где a — длина прямоугольника, d — диагональ.

Пример. Дан прямоугольник с длиной равной 20 см, в котором проведены диагонали
длиной 25 см. Чтобы найти нужную величину, подставляем значения в формулу: β = 2 arcsin 20 / 25 = 2 arcsin 0,8 = 106°.

Тупой угол между диагоналями прямоугольника через длину и ширину

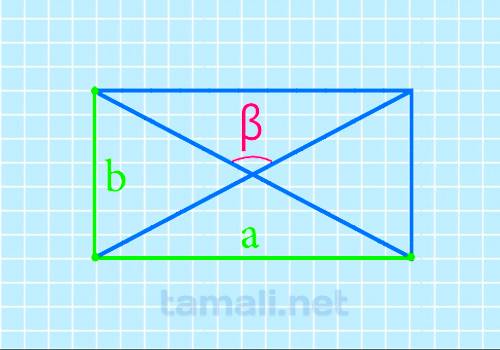
Формула для определения тупого угла между диагоналями прямоугольника через известные значения длины и
ширины такова:

β = 2 arctg a / b

где a — длина прямоугольника, b — ширина прямоугольника.

Пример. Дан прямоугольник со сторонами 15 см и 8 см. Вычислим значение тупого угла,
подставив данные в формулу: β = 2arctg 15 / 8 = 2 arctg 0,5= 123,85°.

Стоит отметить, что при использовании указанных в статье правил нужно владеть знаниями о
тригонометрических функциях. Для того чтобы быстро определять углы, образованные пересечением
диагоналей прямоугольника, поможет именно данный список формул, которые необходимо знать наизусть.
Если на решение задач по геометрии дается небольшой промежуток времени, к примеру, контрольная или
экзамен, лучше отложить сложные алгоритмы и воспользоваться упрощенными формулами.

Параллелограмм относится к выпуклым четырехугольным геометрическим фигурам. Его основные
отличительные признаки от других фигур: равные и попарно параллельные противоположные стороны,
равные противолежащие углы. Диагонали фигуры всегда делятся точкой пересечения на равные отрезки, а
также они делят параллелограмм на 2 одинаковых треугольника. Еще одним главным свойством
четырёхугольника является то, что сумма квадратов диагоналей равна двум суммам квадратов смежных
сторон параллелограмма.

Биссектрисы внутренних углов данного четырёхугольника всегда отсекают от него равнобедренный
треугольник, а также они равны между собой. Сумма углов параллелограмма равна 360°, как и у других
четырёхугольников.
К параллелограммам относятся: квадрат (четырёхугольник с равными сторонами и
равными прямыми внутренними углами), прямоугольники и ромбы (параллелограмм с равными сторонами).
Эти фигуры часто встречаются в школьной программе на уроках геометрии.

Для чего необходимо вычисление угла между диагоналями параллелограмма

• Для нахождения сторон четырёхугольника (длины и ширины).
• Для нахождения площади и периметра фигуры.
• Для нахождения углов между стороной и диагональю.
• Для нахождения длины диагонали.

Знание свойств геометрических фигур помогает справиться с задачей любой сложности. Постоянная
практика с использованием формул способствует быстрому запоминанию информации, помогает проработать
маршруты и теоремы, которые западают.

Прямоугольник часто встречается в решении задач по геометрии. Важно знать все его свойства и уметь
пользоваться правилами и теоремами для успешного нахождения результата. Упрощенные формулы и
несколько конкретных примеров помогут определить правильный алгоритм решения и быстро найти
ответ.

Углы треугольника

Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

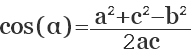
Нахождение углов треугольника по заданным сторонам

Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.

От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.

Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).

Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c” />
a” />
b” />

В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.

Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)

Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.

Треугольник. Формулы и свойства треугольников.

Типы треугольников

По величине углов

По числу равных сторон

Вершины углы и стороны треугольника

Свойства углов и сторон треугольника

Сумма углов треугольника равна 180°:

В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:

если α > β , тогда a > b

если α = β , тогда a = b

Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:

a + b > c
b + c > a
c + a > b

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

a	=	b	=	c	= 2R
sin α	sin β	sin γ

Теорема косинусов

Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 – 2 bc · cos α

b 2 = a 2 + c 2 – 2 ac · cos β

c 2 = a 2 + b 2 – 2 ab · cos γ

Теорема о проекциях

Для остроугольного треугольника:

a = b cos γ + c cos β

b = a cos γ + c cos α

c = a cos β + b cos α

Формулы для вычисления длин сторон треугольника

Медианы треугольника

Свойства медиан треугольника:

В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)

Медиана треугольника делит треугольник на две равновеликие части

Треугольник делится тремя медианами на шесть равновеликих треугольников.

Формулы медиан треугольника

Формулы медиан треугольника через стороны

m_a = 1 2 √ 2 b 2 +2 c 2 – a 2

m_b = 1 2 √ 2 a 2 +2 c 2 – b 2

m_c = 1 2 √ 2 a 2 +2 b 2 – c 2

Биссектрисы треугольника

Свойства биссектрис треугольника:

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.

Формулы биссектрис треугольника

Формулы биссектрис треугольника через стороны:

l_a = 2√ bcp ( p – a ) b + c

l_b = 2√ acp ( p – b ) a + c

l_c = 2√ abp ( p – c ) a + b

где p = a + b + c 2 – полупериметр треугольника

Формулы биссектрис треугольника через две стороны и угол:

l_a = 2 bc cos α 2 b + c

l_b = 2 ac cos β 2 a + c

l_c = 2 ab cos γ 2 a + b

Высоты треугольника

Свойства высот треугольника

Формулы высот треугольника

h_a = b sin γ = c sin β

h_b = c sin α = a sin γ

h_c = a sin β = b sin α

Окружность вписанная в треугольник

Свойства окружности вписанной в треугольник

Формулы радиуса окружности вписанной в треугольник

r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )

Окружность описанная вокруг треугольника

Свойства окружности описанной вокруг треугольника

Формулы радиуса окружности описанной вокруг треугольника

R = S 2 sin α sin β sin γ

R = a 2 sin α = b 2 sin β = c 2 sin γ

Связь между вписанной и описанной окружностями треугольника

Средняя линия треугольника

Свойства средней линии треугольника

MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC

MN || AC KN || AB KM || BC

Периметр треугольника

Периметр треугольника ∆ ABC равен сумме длин его сторон

Формулы площади треугольника

Формула Герона

Равенство треугольников

Признаки равенства треугольников

Первый признак равенства треугольников — по двум сторонам и углу между ними

Второй признак равенства треугольников — по стороне и двум прилежащим углам

Третий признак равенства треугольников — по трем сторонам

Подобие треугольников

∆MNK => α = α ₁, β = β ₁, γ = γ ₁ и AB MN = BC NK = AC MK = k ,

где k – коэффициент подобия

Признаки подобия треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

[spoiler title=”источники:”]

http://planetcalc.ru/534/

http://ru.onlinemschool.com/math/formula/triangle/

[/spoiler]

Треугольник является базовой фигурой геометрии, встречающейся повсеместно. Расчет всех геометрических фигур и тел основаны на наличии в них тех или иных треугольников, благодаря чему становится возможным применить множество теорем и формул, несвойственных конкретным фигурам по отдельности. Равносторонние треугольники, равнобедренные треугольники и прямоугольные треугольники составляют каркас решения геометрических задач, и обладая множеством дополнительных построений внутри треугольника, они предоставляют огромное количество значений тех или иных длин. Все биссектрисы, медианы, высоты, радиусы окружностей, вписанных или описанных около таких треугольников, можно рассчитать в этом разделе через геометрический калькулятор. Для этого необходимо ввести любые имеющиеся вводные данные, и калькулятор выдаст не только значения всех остальных параметров треугольника, но и объяснит преобразования формул, использованные для этих расчетов.

Информация по назначению калькулятора

Треугольник – это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.

В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.

Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.

Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:

⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° – это правильный многоугольник.

⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник – это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.

⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.

Треугольники также могут быть классифицированы в соответствии с их внутренними углами:

⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны – катеты треугольника.

⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).

⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник – это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.

⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.

Онлайн калькулятор поможет найти параметры треугольника, такие как:

• Длины сторон

– равны в равностороннем треугольнике

• Углы

– также равны в равностороннем треугольнике

• Высота

– это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)

• Периметр

– равен сумме всех 3х сторон (P=AB+BC+AC)

• Площадь

– равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)

• Медианы
• Биссектрисы
• Радиус Вписанной и Описанной окружностей
• Диаметр Вписанной и Описанной окружностей
• Длина Вписанной и Описанной окружностей
• Площадь Вписанной и Описанной окружностей

Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:

1. Найти все стороны треугольника.
2. Найти все углы треугольника.
3. Найти площадь (S) и периметр (P) треугольника.
4. Найти радиус (r) вписанной окружности.
5. Найти радиус (R) описанной окружности.
6. Найти высоту (h) треугольника.

Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
 

Сторона треугольника (или длина сторон) может быть найдена различными методами. 
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.

Как найти длину стороны треугольника?

Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.

Для прямоугольного треугольника:

1) Найти катет через гипотенузу и другой катет

где a и b – катеты, с – гипотенуза.

2) Найти гипотенузу по двум катетам

где a и b – катеты, с – гипотенуза.

3) Найти катет по гипотенузе и противолежащему углу

где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.

4) Найти гипотенузу через катет и противолежащий угол

где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.

Для равнобедренного треугольника:

1) Найти основание через боковые стороны и угол между ними

где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.

2) Найти основание через боковые стороны и угол при основании

где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.

3) Найти боковые стороны по углу между ними

где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.

4) Найти боковые стороны по углу при основании

где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.

​​​​​Для равностороннего треугольника:

1) Найти сторону через площадь

где a – искомая сторона, S – площадь треугольника.

2) Найти сторону через высоту

где a – искомая сторона,h – высота треугольника.

3) Найти сторону через радиус вписанной окружности

где a – искомая сторона,r – радиус вписанной окружности.

4) Найти сторону через радиус описанной окружности

где a – искомая сторона,R – радиус описанной окружности.

​​​​​Для произвольного треугольника:

1) Найти сторону через две известные стороны и один угол (теорема косинусов)

где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.

2) Найти сторону через одну известную сторону и два угла (теорема синусов)

где a – искомая сторона, b – известная сторона, α° и β° известные углы.

Скачать все формулы в формате Word