Как найти угол дифракции для линии

Как найти угол дифракции для линии

Как определить угол дифракции

Световые волны отклоняются от своего прямолинейного пути при прохождении через малые отверстия или мимо таких же малых препятствий. Это явление возникает, когда размеры препятствий или отверстий сравнимы с длиной волны, и называется дифракцией. Задачи на определение угла отклонения света приходится решать чаще всего применительно к дифракционным решеткам – поверхностям, в которых чередуются прозрачные и непрозрачные участки одинаковых размеров.

Как определить угол дифракции

Инструкция

Выясните период (d) дифракционной решетки – так называют суммарную ширину одной прозрачной (a) и одной непрозрачной (b) ее полос: d = a+b. Эту пару обычно называют одним штрихом решетки, а измеряют в количестве штрихов на один миллиметр. Например, дифракционная решетка может содержать 500 штрихов на 1 мм, и тогда d = 1/500.

Для вычислений имеет значение угол (α), под которым свет падает на дифракционную решетку. Он отсчитывается от нормали к поверхности решетки, а в формуле участвует синус этого угла. Если в исходных условиях задачи сказано, что свет падает по нормали (α=0), этой величиной можно пренебречь, так как sin(0°)=0.

Выясните длину волны (λ) падающего на дифракционную решетку света. Это одна из наиболее важных характеристик, определяющих угол дифракции. Нормальный солнечный свет содержит целый спектр длин волн, но в теоретических задачах и лабораторных работах, как правило, речь идет о точечном участке спектра – о «монохроматическом» свете. Видимой области соответствуют длины примерно от 380 до 740 нанометров. Например, один из оттенков зеленого цвета имеет длину волны, равную 550нм (λ=550).

Прошедший через дифракционную решетку свет отклоняется на разные углы, образуя при этом неоднородную картину распределения с чередующимися максимумами и минимумами освещенности – дифракционный спектр. Каждому максимуму соответствует собственный угол дифракции. Выясните: угол которого максимума (k) требуется рассчитать. Отсчет ведется от нулевого – центрального – уровня. Например, условия могут требовать расчета искомой величины для второго (k=2) максимума дифракционного спектра.

Воспользуйтесь формулой, связывающей длину волны падающего на дифракционную решетку света с углом дифракции (φ) максимумов определенного порядка: d*(sin(φ)-sin(α)) = k*λ. Выведите из нее определение угла φ – у вас должно получиться такое равенство: φ = arcsin(sin(α)+(k*λ)/d). Подставьте определенные на предыдущих шагах значения в эту формулу и произведите расчеты.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Методика определения углового положения дифракционной линии.

Измерения
на дифрактограмме позволяют получить
профиль дифракционной линии как функцию
угла дифракции 2
двумя способами: как непрерывный график
или как дискретный график. В качестве
параметров характеризующих положение
линии, наиболее часто используется
положение максимума 2m
и центра тяжести дифракционной линии
2с.

Положение
2m
в простейшем
случае определяют как положение середины
хорды, проведённой параллельно линии
фона на высоте 1/3
– 1/2
от основания линии (соответственно Н/3
или Н/2-метод
)

Обычно
регистрацию дифрактограммы ведут с
применением селективно-поглощательного
фильтра на K
излучении. При измерении положения
-пиков
возникают трудности за счёт существования
1-2
дублета. Дублет разрешается тем лучше,
чем больше угол ,
меньше скорость перемещения детектора,
меньше входная щель детектора и
совершеннее строение изучаемых образцов.
В зависимости от степени разрешения
дублета, положение линии измеряют в
различных точках профиля, и измерения
отвечают различным длинам волн: 1,
2
и =(21+2)/3
– средневзвешенной длине волны,
соответствующей центру тяжести
спектральной линии с
с учётом соотношения интенсивностей
IK1:IK2
= 2:1.

Сначала
измеряют положение единой 
– линии, а когда появляется возможность
разрешить 1
и 2
т.е. когда интенсивность во впадине
между ними становится ниже Н/3
или Н/2
то следует измерять уже положение 1.
Если при измерениях отсчёт выполняется
как по 
так и по 1,
то необходимо перейти к одной системе
для проведения расчётов:
.
Точность определения 2m
снижается с ростом асимметрии и ширины
дифракционной линии.

Метод
определения положения центра тяжести
дублета 2с
свободен от указанных выше сложностей.
Координата центра тяжести определяется
выражением

,
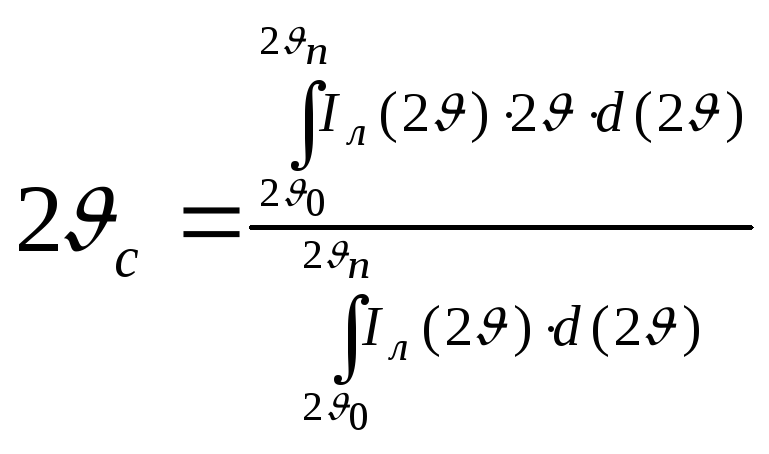где 20
и 2n
– соответственно
начальный и конечный углы при которых
профиль дифракционной линии переходит
в фон; Iл(2)
– распределение интенсивности по
профилю линии за вычетом фона. Если
регистрация линии велась по «точкам»
с постоянным шагом (2),
то переходя от интегрированию к
суммированию с учётом того, что текущее
угловое положение детектора

2i=20+i
(2),
где i
– номер шага, получим

,
где Iл(2i)=I(2i)-Iф(2i)
– интенсивность линии, за вычетом полной
интенсивности фона в точке 2i;
n
– число шагов перемещения детектора.
Предполагается, что интенсивность фона
меняется линейно.

При
расчётах с использованием 2с
необходимо применять значение длины
волны .

Точность
измерения как при расчёте по 2m,
так и по 2с
существенно зависит от относительной
погрешности измерения интенсивности
уровня фона на дифрактограмме.

Обработка результатов по индицированию.

Съёмка
дифрактограммы с образца вольфрама
производилась в шаговом режиме. Далее
программа ЭВМ автоматически обрабатывала
полученные данные, в зависимости от
выбранного диапазона расположения
дифракционной линии и от степени
полинома, аппроксимирующего фон,
выводился результат: расположение
центра тяжести дублета 2с,
максимум интенсивности профиля дублета
за вычетом фона, межплоскостное
расстояние.

Была произведена
обработка результатов для 4-х диапазонов
различной ширины, для определения
зависимости погрешности от ширины
диапазона выборки линии. Полученные
данные можно представить в виде таблицы:

Диапазон
20-2n

50-70

55-60

53,625-62,75

57-59

Точность
определения 2с

0,0769

0,0128

0,0252

0,0046

Видна
закономерность, показывающая что при
лучшем указании границ, где профиль
линии переходит в фон, точность определения
центра тяжести лучше.

Также
была произведена обработка результатов
при различной степени полинома
аппроксимирующего фон. Результаты можно
представить в виде таблицы:

Степень
полинома фона

1

2

3

Точность
определения 2с

0,0101

0,0147

0,0176

Ухудшение точности
определения центра тяжести при увеличении
степени полинома может быть связана с
низким значением степени (2-3) возможно
при более высоких степенях показатель
точности оказался бы лучше чем при
аппроксимации полиномом первой степени.

Аналитическое
индицирование сводится к расчёту Qi.
Полученный ряд значений углов:

2c

40,1597

58,1656

73,1588

86,9994

100,6744

115,1365

131,3075

153,8737

d(hkl)

2,0520

1,5861

1,2936

1,1199

1,0014

0,9060

0,8461

0,7914

Imax

1687

1159

985

1595

839

284

Qэi

1,00

2,00

3,01

4,02

5,03

6,05

7,04

8,06

(HKL)

110

200

211

220

310

222

321

400

Поскольку
расхождение с теоретическим рядом для
ОЦК только во втором знаке после запятой,
то можно с высокой степенью достоверности
сказать что вольфрам имеет ОЦК решётку.

Соседние файлы в папке Лабораторные работы

  • #
  • #
  • #
  • #
  • #
  • #
Источник

Enter the number of slits, the wavelength, and the distance between slits into the Diffraction Angle Calculator. The calculator will evaluate the Diffraction Angle. 

  • Diffraction Limit Calculator
  • Grating Density Calculator
  • Diffraction Efficiency Calculator

Diffraction Angle Formula

The following formula is used to calculate the Diffraction Angle. 

Variables:

  • DA is the Diffraction Angle (degrees)
  • n is the number of slits 
  • w is the wavelength 
  • d is the distance between slits 

To calculate the diffraction angle multiply the number of slits by the wavelength, divide by the distance between slits, then take the inverse sine of the result.

How to Calculate Diffraction Angle?

The following steps outline how to calculate the Diffraction Angle.

  1. First, determine the number of slits.
  2. Next, determine the wavelength. 
  3. Next, determine the distance between slits. 
  4. Next, gather the formula from above = DA = SIN^-1(n*w/d).
  5. Finally, calculate the Diffraction Angle.
  6. After inserting the variables and calculating the result, check your answer with the calculator above. 

Example Problem:

Use the following variables as an example problem to test your knowledge.

number of slits = 5

wavelength = 6

distance between slits = 10

DA = SIN^-1(n*w/d) =  ?

Источник


  •
  • 0




На дифракционную решетку нормально падает монохроматический свет. Определить угол дифракции для линии с длиной волны 0,55 мкм в спектре четвертого порядка, если угол дифракции для линии с длиной волны 0,6 мкм в спектре третьего порядка составляет 30.

  • Комментариев (0)



  • 0


Уравнение решетки:
d·sin α = m·λ

В первом случае:
d·sin α = 4·0,55*10⁻⁶                (1)

Во втором случае:
d·sin 30° = 3·0,6*10⁻⁶               (2)

Разделим (1) на (2):

sin α / sin 30° = 4*0,55 / (3*0,6)

sin α / 0,5 = 1,2222

sin α = 1,2222*0,5 = 0,6111

α ≈ 38°

  • Комментариев (0)

Источник

Максимум второго
порядка при освещении дифракционной решетки монохроматическим светом
наблюдается под углом 16,4ͦ. Чему равен угол дифракции для максимума,
соответствующему максимальному порядку образующегося спектра?

Решение.

Из формулы
дифракционной решетки dsinj1 = m1l найдем период решетки d = m1l/dsinj1 , где m1 = 2, j1 = 16,4ͦ.

Максимальный порядок
дифракционного спектра будет равен ближайшему целому числу при j = 90ͦ. (смотрите тут)

mmax
= d/l
= m1l/sinj1l = m1/sinj1 = 2/sin16,4ͦ =
7,1.

mmax –
целое число. Поэтому mmax
= 7. Угол дифракции j2 находим следующим образом:

dsinj2 = mmaxl или
m1l•sinj2/sinj1 = mmaxl;

sinj2 = mmaxsinj1/m1 =
7sin16,4ͦ/2 = 0,988;

j2 = arcsin0,988 ≈ 81ͦ.

Ответ: угол дифракции
для максимума равен 81ͦ.

Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.

Источник

Добавить комментарий