Как найти угол дифракции первого порядка

Как определить угол дифракции

Световые волны отклоняются от своего прямолинейного пути при прохождении через малые отверстия или мимо таких же малых препятствий. Это явление возникает, когда размеры препятствий или отверстий сравнимы с длиной волны, и называется дифракцией. Задачи на определение угла отклонения света приходится решать чаще всего применительно к дифракционным решеткам – поверхностям, в которых чередуются прозрачные и непрозрачные участки одинаковых размеров.

Инструкция

Выясните период (d) дифракционной решетки – так называют суммарную ширину одной прозрачной (a) и одной непрозрачной (b) ее полос: d = a+b. Эту пару обычно называют одним штрихом решетки, а измеряют в количестве штрихов на один миллиметр. Например, дифракционная решетка может содержать 500 штрихов на 1 мм, и тогда d = 1/500.

Для вычислений имеет значение угол (α), под которым свет падает на дифракционную решетку. Он отсчитывается от нормали к поверхности решетки, а в формуле участвует синус этого угла. Если в исходных условиях задачи сказано, что свет падает по нормали (α=0), этой величиной можно пренебречь, так как sin(0°)=0.

Выясните длину волны (λ) падающего на дифракционную решетку света. Это одна из наиболее важных характеристик, определяющих угол дифракции. Нормальный солнечный свет содержит целый спектр длин волн, но в теоретических задачах и лабораторных работах, как правило, речь идет о точечном участке спектра – о «монохроматическом» свете. Видимой области соответствуют длины примерно от 380 до 740 нанометров. Например, один из оттенков зеленого цвета имеет длину волны, равную 550нм (λ=550).

Прошедший через дифракционную решетку свет отклоняется на разные углы, образуя при этом неоднородную картину распределения с чередующимися максимумами и минимумами освещенности – дифракционный спектр. Каждому максимуму соответствует собственный угол дифракции. Выясните: угол которого максимума (k) требуется рассчитать. Отсчет ведется от нулевого – центрального – уровня. Например, условия могут требовать расчета искомой величины для второго (k=2) максимума дифракционного спектра.

Воспользуйтесь формулой, связывающей длину волны падающего на дифракционную решетку света с углом дифракции (φ) максимумов определенного порядка: d*(sin(φ)-sin(α)) = k*λ. Выведите из нее определение угла φ – у вас должно получиться такое равенство: φ = arcsin(sin(α)+(k*λ)/d). Подставьте определенные на предыдущих шагах значения в эту формулу и произведите расчеты.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Дифракция
на одной щели.

При
нормальном падении лучей на щель шириной
a

условие
дифракционных максимумов

a
sin 
= (2k+1)
/2
, (k=1,
2, 3 …)

условие
дифракционных минимумов

a
sin 
= k
, (k=1,
2, 3 …)

Дифракция
на плоской дифракционной решетке.

При
нормальном падении лучей на решетку с
периодом d

условие
главных дифракционных максимумов

d
sin 
= k

, (k=1,
2, 3 …)

условие
добавочных минимумов

d
sin 
= k
/N
,

где
N
– число щелей (штрихов решетки), k
= 1, 2, 3
… , кроме значений k
= N,
2N,
3N
…

Разрешающая
способность дифракционной решетки

R
= /(
)
= kN,

где

– наименьшая разность длин волн двух
соседних спектральных линий (
и 
+
),
при которой эти линии могут быть видны
раздельно.

Угловая дисперсия дифракционной решетки

D_
= d

/ d
= k
/ (d

cos ).

Линейная
дисперсия дифракционной решетки D_l
=

.

Для
малых углов дифракции D_l

FD_
,

где
F
– фокусное расстояние линзы, собирающей
на экране дифракционную картину.

Примеры решения задач

Задача
6. На пути
луча, идущего в воздухе, поставили
диафрагму с круглым отверстием,
пропускающим: 1) половину первой зоны
Френеля; 2) первую зону Френеля; 3) первые
полторы зоны Френеля. Как изменилась
при этом интенсивность света в точке
наблюдения, находящейся на оси отверстия?

Решение

а	б	в	г
	Рис. 6

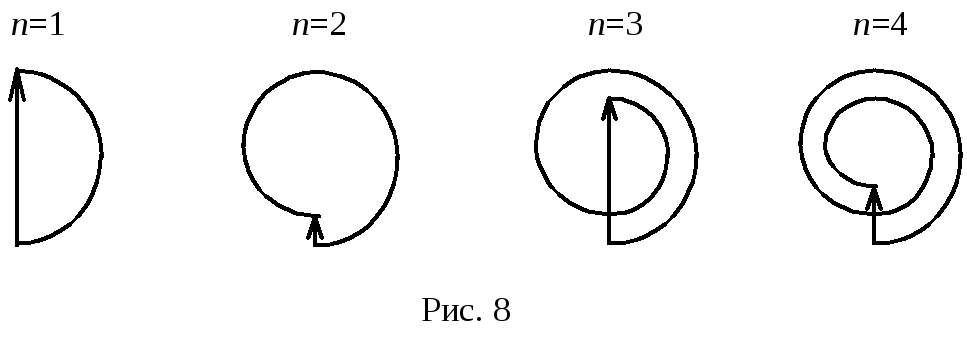
1)
Задачу решаем методом графического
сложения амплитуд. В случае, когда идет
луч в воздухе, векторная диаграмма имеет
вид, представленный на рис. 6, а. Вектор,
соединяющий начало диаграммы (т. О) с
конусом (т. А), является вектором амплитуды
колебания, возбуждаемого в точке
наблюдения всей волновой поверхностью.

На
рис.6,б представлена векторная диаграмма,
соответствующая случаю, когда отверстие
пропускает половину первой зоны Френеля.
Световой эффект в этом случае определяется
вектором
.

Из
рис. 6 видно, что ОВ = ОА / (cos45˚) = OA.
Интенсивность световой волны
пропорциональна квадрату ее амплитуды
J~A²,
следовательно, интенсивность света в
первом случае (рис. 6, а) J₁~ОA²,
во втором случае (рис. 6, б) J₂~ОВ².

,
следовательно, интенсивности увеличиваются
в два раза.

2)
Во второй задаче отверстие пропускает
первую зону Френеля. Векторная диаграмма
для этого случая представлена на рис. 6,
в. Результирующая амплитуда – вектор
ОС.
Из рис. 6, в видно, что ОС=2 · ОА,
следовательно,
,
то есть интенсивность увеличивается в
4 раза.

3)
Векторная диаграмма для решения третьей
задачи представлена на рис. 6, г.
Результирующий вектор амплитуды –
вектор ОD.
Сравнение рис. 6, б и 6, г показывает, что
ОD
= ОВ, следовательно, ответ будет такой
же, как на первый вопрос задачи.

Ответ:
1) увеличивается в 2 раза;

2) увеличивается
в 4 раза;

3) увеличивается
в 2 раза.

Задача
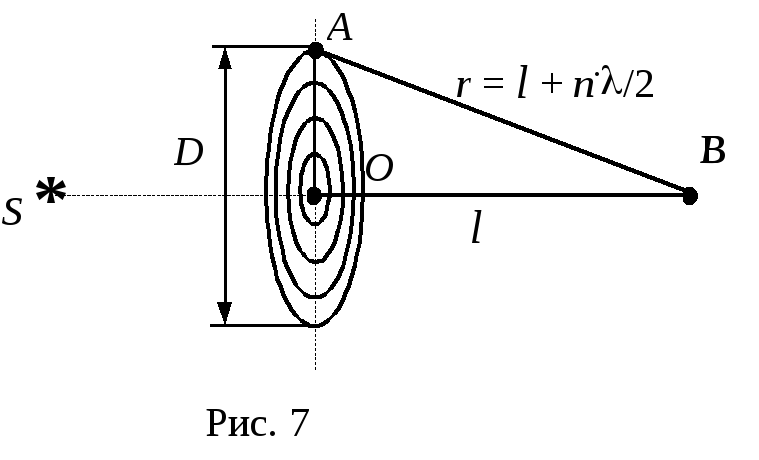
7. На диафрагму
с диаметром отверстия 1,96 мм рис. 7 падает
нормально параллельный пучок
монохроматического света (=600
нм). При каком наибольшем расстоянии
между диафрагмой и экраном в центре
дифракционной картины еще будет
наблюдаться темное пятно?

Дано: D = 1,96 мм  = 600 нм	Решение
lmax –?

Так
как на диафрагму падает параллельный
пучок монохроматического света, то
фронт этих лучей –
плоскость.
Диафрагма будет вырезать из плоскости
волнового фронта кружок диаметром D,
в котором укладывается определенное
число (n)
зон Френеля. Расстояние АВ = r =
l
+ n^./2.

Из
треугольника ОАВ

(l
+
n·/2)²
=
(D/2)²
+ l²
,

l²
+
l·n·
+ n^2
. (
²/4)
= D²/4+
l².

Ввиду
малости величины 
(
<< l)
величиной ²
можно пренебречь, тогда

n
= D²/(4
l).

Последняя
формула свидетельствует о том, что с
увеличением расстояния между диафрагмой
и экраном число зон Френеля, укладывающихся
в отверстии диафрагмы, изменяется. От
того, четное или нечетное число зон
Френеля укладывается в отверстии
диафрагмы, зависит результат дифракции:
при четном числе наблюдается минимум,
при нечетном – максимум.

Зависимость
интенсивности света в центре дифракционной
картины от расстояния между диафрагмой
и экраном представлена на рис. 9.

Из рис. 9 видно, что интенсивность максимумов падает, а интенсивность минимумов растет, приближаясь к интенсивности при полностью открытом фронте (n). При приближении к диафрагме

последний
минимум наблюдается при числе открытых
зон Френеля n=2,
это соответствует искомому расстоянию
l_max.
Подставляя значение n=2
в последнюю формулу, получим

2
= D²
/(4 l_max
),
откуда l_max
= D²
/( 8 )
.

l_max
= (1,96)^2
. 10^‑6
/(8 6 ^.
10^‑7)
=0,8 (м).

Ответ:
l_max
= 0,8 (м).

Задача
8. На
дифракционную решетку шириной 1 см
падает нормально белый свет. Спектр
проектируется линзой на экран, отстоящий
от решетки на 3 м. Ширина спектра первого
порядка 66 см. Определить: 1) постоянную
решетки; 2) общее число главных максимумов,
даваемых решеткой; 3) разрешающую
способность решетки для максимума
наибольшего порядка. Границы видимости
спектра _кр = 780 нм,
_ф = 400 нм.

Дано: L=1 см=10‑2 м F=3 см=3.10‑2 м кр=780 нм=7,80.10–7м ф = 400 нм=4.10–7м	Решение Рис. 10
1) d – ? 2) N – ? 3) R – ?

На
рис.10 _ф
– угол дифракции, соответствующий углу
отклонения от первоначального направления
фиолетовых лучей, _кр
– красных лучей. В точке О
(центре дифракционной картины) собираются
лучи, прошедшие дифракционную решетку
без отклонения (=0).
В этой точке наблюдается центральный
дифракционный максимум.

l_ф
–
расстояние от центрального максимума
до фиолетовой линии первого порядка,
l_кр
– до
красной линии; 
l
– длина
спектра первого порядка. Так как углы
дифракции первого порядка малы, можно
считать, что

sin


tg 


(рад).

Из
рисунка видно, что

_ф

l_ф
/F
; _кр

l_кр
/F
; 
l
= l_кр–
l_ф
= F(_кр
– _ф).

Постоянная
решетки d,
длина волны 
и угол дифракции 
связаны между собой соотношением

dsin
= k
(условие главного максимума),

где
k
– порядок максимума.

По
условию задачи k
=1, sin


= /d.

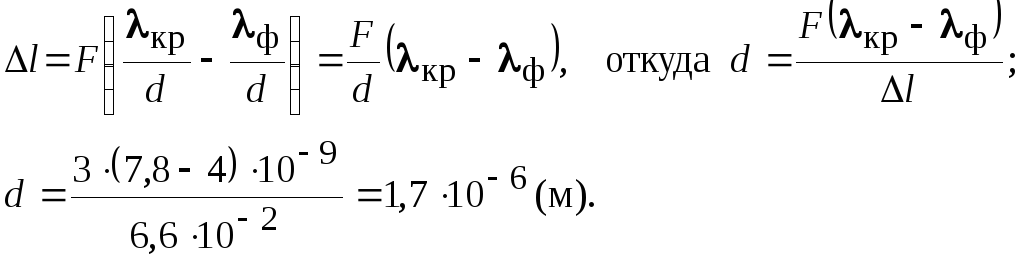
Общее
число главных максимумов, даваемых
решеткой, определяется максимальным
порядком k_max
и равно N_max=2
k_max+1,
так как дифракционная картина симметрична:
число максимумов справа от центрального,
слева от центрального и сам центральный
максимум. Максимальный порядок, даваемый
решеткой, получим из условия дифракционного
максимума, положив sin
= 1, так как угол отклонения лучей решеткой
не может превышать 90˚,
при этом

k_max=d/_min;
k_max=1,7^.10^‑6/4^.10^–7=4,(25),
то есть максимальный порядок равен 4
(всегда округляем в сторону уменьшения,
так как максимум следующего порядка не
виден).

Общее
число главных дифракционных максимумов

N_max
= 2 ^.
4 + 1 =9.

Разрешающая
способность дифракционной решетки
определяется соотношением

R
= k
^.
N,

где
N
– общее число штрихов (щелей) решетки,
k
– порядок дифракционного максимума.

По
условию задачи k = k_max
= 4.
Число щелей найдем из ширины L
дифракционной решетки, так как L=N
^. d
,

N=L/d.

R
= k_max
^.
L/d;

R
= (4^.
10–2)/(1,7^.10^–6)
= 23529.

Ответ:
d
= 17 мкм, N_max
= 9, R
= 23529.

Задача
9. Минимальное
значение угловой дисперсии некоторой
дифракционной решетки D=1,266^.10^–3
рад/нм. Найти угловое расстояние между
линиями с ₁=480 нм
и ₂=680 нм
в спектре первого порядка.

Дано: D=1,266.10–3 рад/нм 1=480нм=4,8.10–7 м 2=680нм=6,8.10–7 м k =1	Решение Угловое расстояние между линиями равно разности углов дифракции, соответствующих этим линиям  = 2 – 1.
 – ?	Угловая дисперсия определяется соотношением D=k /(d . cos ).

Минимальное
значение угловой дисперсии соответствует
минимальному значению k=1
и максимальному значению cos

=1, то есть

D_min
=1/d,

следовательно,
можно определить период решетки

d=1/
D_min;

d=1/
1,266 ^.10^‑6=7,9
^.10^‑7
(м).

Из
условия дифракционного максимума

d
sin
₁
= ₁
(k=1
по условию задачи )

d
sin ₂
= ₂

sin
₁
= ₁/d
=4,8^.10^‑7/7,9
^.10^‑7
=0,6; ₁

37˚;

sin
₂
= ₂/d
=4,8^.10^‑7/7,9
^.10^‑7
=0,6; ₂

59˚;

 =
59˚
– 37˚=22˚.

Ответ:

= 22˚.

Задача
10. Будут ли
разрешены дифракционной решеткой,
имеющей 100 штрихов, спектральные линии
с длиной волн ₁=598нм
и ₂
= 602 нм в
спектре а) первого б) второго порядка?

Дано: N=100 1=598нм=5,98.10‑7м 2=602нм=6,02.10‑7м k=1, k=2	Решение Разрешающая способность дифракционной решетки R==/()=k N, (1) где  – наименьшая разность длин волн двух спектральных линий, при которой эти линии могут быть видны раздельно в спектре,
R – ?	полученном посредством данной решетки.

Если
разность длин волн 
< ,
две линии сливаются в одну, то есть не
разрешаются дифракционной решеткой.

Для
порядка k=1
R₁=1^.100=100,
для порядка k=2
R₂=2^.100=200.

В
формуле (1) 
=₂
– ₁=602
– 598 = 4 (нм);

 =(₂
+ ₁)/2
= 600 (нм);

 /
= 600(нм)/4(нм)=150, что больше R₁
и меньше R₂.

Это
означает, что для первого порядка 
< 
и указанные в условии задачи линии не
разрешаются данной дифракционной
решеткой.

Для
второго порядка 
> 
и линии видны раздельно.

Ответ:
а) не разрешены; б) разрешены.

Соседние файлы в папке FIZIKA

• #
• #
• #
• #
• #
• #
• #

Введение

Дифракционные решетки – очень полезный и популярный инструмент в спектроскопии. Благодаря свойству преломлять свет под различными углами, можно получать монохроматические пучки от обычных источников белого cвета. Связь между углами падения, дифракции и длиной волны описывается с помощью общеизвестного уравнения дифракционной решетки, из которого путем простых алгебраических операций можно найти рассеяние, разрешение и область свободной дисперсии конкретного элемента.

Уравнение решетки

Пучок света при попадании на решетку подвергается дифракции, то есть раскладывается на несколько частей. Направление каждой компоненты зависит от длины волны и угла, под которым излучение попадает на решетку. Также имеет значение профиль и глубина штрихов, нанесенных на решетку.

Уравнение решетки полностью описывает свойства прибора, его можно записать как:

        (1) 

где α – угол падения, β_m – угол дифракции (за положительное направление принимается угол против часовой стрелки, за отрицательное – по часовой), m – порядок дифракции (любое целое число), d – период решетки или частота штрихов (обычно измеряется как число штрихов на миллиметр, в исключительных случаях приводится пересчет в нанометры), λ – длина волны падающего излучения.

Порядок дифракции

Нулевой порядок дифракции означает равенство угла падения α углу дифракции β₀, и все уравнение преобразуется в известный закон отражения. Это решение всегда возможно, но на практике отраженный луч не особенно важен. Отраженное излучение – причина потерь излучения при прохождении через решетку. В монохроматорах, спектрометрах и спектрографах в основном используется порядок дифракции m = -1. Решетки с малой частотой штрихов (соответствует большим периодам) создают больше порядков дифракции. Дифракционные решетки могут использоваться как делители монохроматических пучков одного или двух источников.

Светорассеяние

Угловая дисперсия характеризует величину изменения угла дифракции за единицу изменения длины волны. Измеряется как угловое расстояние между смежными длинами волн. Выражение угловой дисперсии определяется как производная левой части уравнения решетки при фиксированном угле падения:

         (2)

Повысить дисперсию возможно с помощью увеличения частоты штрихов либо с помощью решетки с крупно нарезанными штрихами. В основном используются решетки с мелкими штрихами, поскольку для практических применений обычно необходим более широкий спектр.

Волновая дисперсия выходной щели спектроскопического прибора обычно определяется как обратная линейная дисперсия в нано- или миллиметре. Фокусное расстояние прибора обозначается как f, и тогда общая формула обратной линейной дисперсии принимает вид:

         (3)

Габариты оптической системы зависят в том числе и от фокусного расстояния. Наиболее компактными считаются голографические дифракционные решетки с высокой частотой штрихов.

Рассеяние света также важная характеристика дифракционных решеток. Данная характеристика определяет предел обнаружения.

Голографические решетки отличаются меньшим светорассеянием и полным отсутствием «ложных» спектров на картине, поскольку метод голографической записи дает более точные промежутки между интерференционными полосами (штрихами). Однако если используются источники рассеянного света, светорассеяние голографической решетки повысится.

Область свободной дисперсии

Из уравнения дифракционной решетки можно вывести следующую закономерность: длина волны падающего света λ соответствует первому порядку дифракции, λ/2 – второму порядку дифракции, λ/3 – третьему и т. д. Очень часто при использовании решеток нужно каким-либо образом ограничивать порядки дифракции: например, с помощью полосового фильтра, либо используя ограниченный диапазон длин волн источника света или приемника.

Область свободной дисперсии дифракционных решеток, или свободная спектральная область – это максимальный интервал длин волн, который можно наблюдать при использовании данной дифракционной решетки (и в конкретном порядке дифракции) без переналожения соседних порядков спектра. Если λ₁ – нижний предел (наименьшая длина волны), λ₂ – верхний предел (наибольшая длина волны), тогда область свободной дисперсии выражается с помощью уравнения:

        (4) 

Очевидно, свободная спектральная область уменьшается пропорционально росту порядка дифракции. Так, например, порядок дифракции решетки m = -1 соответствует области свободной дисперсии величиной λ₂/2. Это значит, что в диапазоне от λ₁ до 2λ₁ не будет наблюдаться переналожения спектров до второго порядка.

Разрешающая способность

Спектральное разрешение дифракционной решетки Δλ определяется как расстояние между двумя пиками спектральных полос, которые только могут быть обнаружены приемником как раздельные. Из теории известно, что дифракционные решетки имеют предел разрешения, обусловленный свойствами конкретного прибора и источника.

Разрешающая способность дифракционной решетки есть безразмерное число R. Краткая формула имеет вид:

        (5) 

где m – порядок дифракции, N – общее число штрихов на рабочей поверхности решетки. Как видно из формулы, существует предел произведения порядка дифракции и количества штрихов.

Теоретическое значение разрешающей способности решетки всегда несколько выше реального, поскольку существуют дефекты поверхности решетки и профиля пучка.

В качестве расчетного примера рассмотрим 110-миллиметровую решетку с частотой 1800 штрихов/мм. В первом порядке дифракции теоретическая разрешающая способность равна 198000, спектральное разрешение составляет 0.03 нм при длине волны 500 нм.

Эффективность дифракционной решетки

Абсолютная эффективность определяется как величина падающего потока, который дифрагирует в заданном порядке дифракции. Относительная эффективность связана с коэффициентом отражения зеркала, покрытого тем же составом, что и решетка. Следует отметить, что относительная эффективность всегда выше, чем абсолютная.

В большинстве приложений используется только один порядок дифракции, где «идеальная» решетка обеспечивала бы стопроцентную абсолютную эффективность. Однако эффективность реальной решетки, как правило, является сложной функцией длины волны и поляризации падающего света, также зависит от частоты штрихов, профиля и материала решетки. В случае излучения с поперечной магнитной поляризацией, когда вектор электрического поля перпендикулярен штрихам решетки, можно наблюдать быстрые скачки эффективности даже при небольшом изменении длины волны. Этот феномен был впервые обнаружен Р. В. Вудом в 1902 году, поэтому скачки эффективности дифракционной решетки обычно называют аномалиями Вуда.

Синусоидальные решетки

Синусоидальный профиль штрихов характерен для голографического метода изготовления дифракционных решеток. Кривая эффективности голографической решетки в отличие от решетки, изготовленной традиционным методом нарезки, более гладкая и однородная.

Эффективность рассчитывается для конкретной спектральной области, аналогично рассчитывается глубина штрихов. Большую глубину нарезки имеют решетки с высокой частотой штрихов. Когда расстояние между канавками менее, чем в 1.25 раз меньше рабочей длины волны, существуют только порядки дифракции -1 и 0, а если решетка имеет соответствующий профиль штрихов, большая часть дифрагированного света переходит в порядок -1. В этой области голографические дифракционные решетки дают более 50% абсолютной эффективности.

Отражательная дифракционная решетка

Отражательные дифракционные решетки предназначены для конкретной длины волны, рабочий диапазон варьируется от угла решетки. Абсолютная эффективность резко снижается в диапазонах, отличных от рабочего, при этом в рабочей области может составлять примерно 70%.

Перестраивание длины волны лазерного источника

Голографические решетки часто используются для перестраивания длины волны лазера. Решетка выполняет роль селективного торцевого зеркала в резонаторе. При использовании дифракционной решетки для перестраивания длины волны лазерного излучения применяются две основные конфигурации – схема Литтроу и схема скользящего падения (также известна как схема Литтмана).

Конфигурация Литтроу

Решетка установлена так, чтобы свет желаемой длины волны дифрагировал в обратном направлении вдоль падающего излучения, а длина волны распознается вращением решетки. Внутри резонатора обычно используется ахроматическая линза, которая расширяет лазерный пучок, чтобы заполнить как можно большую площадь решетки. В качестве выходного излучения принимается излучение нулевого порядка дифракции. Недостатком этой конфигурации является то, что направление пучка меняется вместе с поворотом решетки.

Конфигурация Литтмана

Решетка фиксируется под углом падения примерно 90°, а длина волны настраивается вращением специального настраивающего зеркала. Дополнительная линза для расширения пучка не требуется, и поэтому можно использовать меньшую решетку. Однако больший угол падения подразумевает, что габаритная ширина решетки должна быть значительно больше, чем протяженность штрихов.

Эффективность схемы Литтмана может быть очень высокой, в особенности если используется входное излучение с поляризацией, перпендикулярной штрихам решетки (поперечной магнитной поляризацией). В случае поперечной электрической поляризации эффективность заметно снижается. 

Компрессия импульса

Когда короткий лазерный импульс передается через оптическое волокно, импульс как бы растягивается или «чирпируется» из-за нелинейных эффектов (явление так называемой фазовой автомодуляции).

Например, импульс падает на решетку с нормальной оптической дисперсией, то есть длинноволновая часть излучения проходит через оптическую систему быстрее, чем коротковолновая. Используя пару решеток, можно найти такое расположение, чтобы длинноволновая часть импульса проходила более длинный путь. В оптимальном случае на выходе образуется ограниченный импульс. Пара решеток не только компенсирует уширение импульса в волокне, но и сокращает его растяжение. Сжатие может достигать 90 раз.

Усиление чирпированного импульса

Очень короткие импульсы (~ 100 фс) генерируются лазерами с синхронизацией мод. Эти импульсы имеют слишком низкую пиковую мощность. Техника усиления чирпированных импульсов позволяет достичь пиковых мощностей порядка ТВт.

Усилитель представляет собой лазерный кристалл внутри резонатора. Чтобы избежать влияния нелинейных эффектов, разрушающих кристаллы, входной импульс расширяется во времени, что приводит к снижению пиковой мощности. Далее чирпированный импульс снова усиливается и затем сжимается для достижения высокой мощности. Нужно также отметить, что длительность выходного импульса в результате практически равна длительности входного.

Расширение и сжатие

Как при растяжении, так и при сжатии используются пары решеток, расположенные в субтрактивном дисперсионном режиме: то есть так, что угловая дисперсия первой решетки вычитается второй решеткой. Два параллельных пучка с разными длинами волн, падающие на первую решетку, остаются параллельными и после прохождения сквозь вторую решетку, несмотря на разницу пройденных расстояний.

Пара решеток, расположенная параллельно, будет вводить отрицательную дисперсию групповой скорости, то есть длинноволновые части излучения приходят позже, чем коротковолновые.

Для достижения положительной дисперсионной задержки необходима более сложная схема, в этом случае система афокальных линз (телескоп) размещается между решетками. Телескоп регулирует знак углов так, чтобы пучки падали на вторую решетку под тем же углом, что и на первую.

Расширитель и компрессор пучка обычно используются в двухпроходном режиме. Из преимуществ этого режима: удвоение дисперсии. Все длинноволновые компоненты пучка становятся коллинеарными, а не линейными, как это происходило бы в режиме одного прохода.

Инструменты для спектроскопии

Стандартный набор для спектроскопических исследований в основном состоит из входной апертуры, коллиматора, рассеивающего элемента, фокусирующих оптических компонентов, в отдельных случаях набор дополняется выходной апертурой. Свет, попадающий на входную щель, в коллиматоре (обычно вогнутое зеркало) преобразуется в параллельный пучок.

Рассеивающий элемент (решетка) отклоняет излучение под углом, зависящим от длины волны. Рассеянный свет фокусируется на плоскости изображения, где и формируется спектр (серия монохроматических изображений входной щели).

Монохроматоры

В монохроматоре установлена выходная апертура, с помощью которой передается очень узкая часть спектра. Входная и выходная щели жестко закреплены, сканирование спектра осуществляется вращением решетки. Итак, решетка работает с постоянным угловым отклонением между падающим и рассеянным светом. Данная схема реализована в большинстве монохроматоров типа Черни-Тернера, Эберта и Литтроу.

Волоконная оптика

Голографические решетки отлично подходят для приложений волоконной оптики благодаря компактным размерам, высокой частоте штрихов, эффективности и угловой дисперсии.

Рамановская спектроскопия и эксперименты по рассеянию лазерного излучения

В исследованиях, связанных с рассеянием лазерного излучения (рамановская спектроскопия и рассеяние Томсона), где требуется диагностика плазмы, требования к решетке очень высоки. Образец освещается лазерным излучением, резонансное рассеяние приводит к появлению слабых спектральных линий, близких к основной полосе. В рамановской спектроскопии интенсивность спектральной картины наиболее низкая, что и является основной проблемой данного метода.

Требуемое разрешение достигается с помощью крупногабаритных приборов с большим фокусным расстоянием, при этом все оптические поверхности должны иметь высочайшее качество. При работе в непосредственной близости от интенсивной спектральной линии аберрации оптической системы и дифракция Фраунгофера от упоров апертуры могут провоцировать значительное светорассеяние.

Решетки Spectrogon с низким уровнем светорассеяния изготавливаются на подложках высокого качества, потому такая решетка практически не будет вносить аберрации. Подобные решетки часто устанавливаются в масс-спектрометрах с двойной или тройной фокусировкой для уменьшения рассеянного света.

Голографические решетки становятся распространенным предпочтением. Нарезные решетки, несмотря на высокое качество, все равно порождают ложные спектры, сильно искажающие исследуемые сигналы.

Спектроскопия поглощения

Абсорбционная спектроскопия является еще одним приложением, в котором низкий уровень светорассеяния голографических решеток имеет большое преимущество. Уровень рассеянного света напрямую связан с диапазоном поглощения прибора, и чем меньше рассеянного света, тем более точный спектр поглощения можно получить.

Источник света в абсорбционной спектроскопии обычно представляет собой широкополосный источник, и поэтому рассеянный свет будет состоять из сплошного спектра. Каждый компонент длины волны падающего света порождает спектр рассеяния, в центре которого находится фактическая длина волны. Результирующий рассеянный свет является суммой всех длинноволновых компонентов.

© Spectrogon

Компания INSCIENCE помогает своим заказчикам решать любые вопросы и потребности по продукции Spectrogon на территории РФ