Как найти угол египетского треугольника

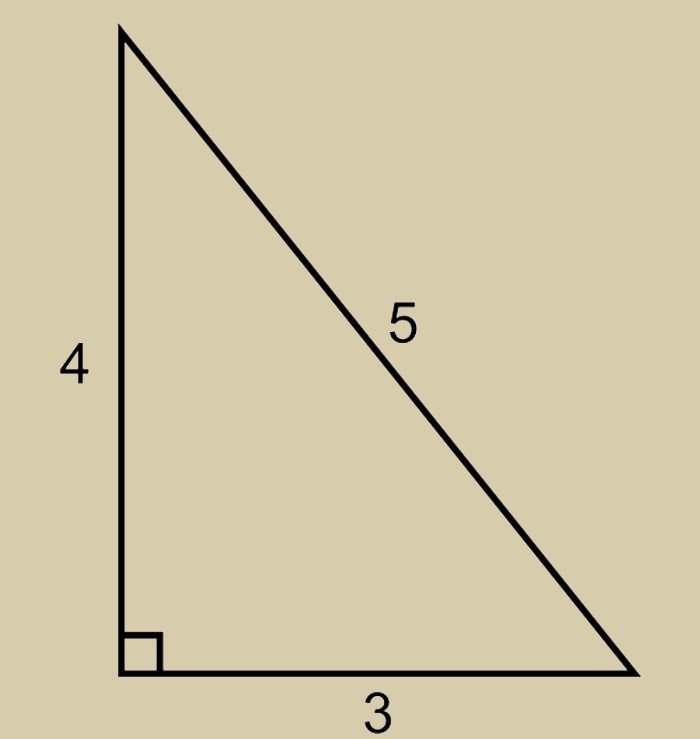
Египетский треугольник – прямоугольный, со сторонами 3, 4 и 5. Эта фигура является простейшей из Героновых треугольников со сторонами равными целым числам, которая одна из первых получила широкое применение.

Почему же он так необычно называется?

Название он получил ещё в Древнем Египте, где активно применялся для построения прямых углов на местности. Это было важно для земледельцев, так как ежегодно разливы Нила размывали границы между полями и приходилось заново размечать их с помощью египетского треугольника. Этот способ не занимал много времени и был доступен всем, достаточно было на верёвке узлами отмерить 12 равных отрезков, а потом из нее сложить треугольник и угол, оказавшийся напротив стороны 5 (гипотенузы), являлся прямым.

Кроме того, этот треугольник применялся для разработки пропорциональных схем и чертежей, что позволяло правильно проецировать центр тяжести пирамид на середину опоры– это гарантировало надёжность строения.

Этот чудо-треугольник имеет ряд замечательных особенностей:

– радиус окружности, вписанной в него, равен единице;

– все стороны состоят из целых чисел;

– для создания можно использовать любые подходящие подручные средства, например, шнур или шест.

Если усерднее покопаться в истории появления этого треугольника, то можно обнаружить, что официально принято считать его создателем – Пифагора. Благодаря долгим измерениям и анализам построенных моделей, греческий математик смог описать все их геометрические свойства.

По просьбе древнегреческого философа и математика Фалеса, Пифагор отправился в Египет, чтобы изучить математические, архитектурные и астрономические наработки египтян. Путешествуя, он впервые увидел высокие и величественные пирамиды, которые поистине поражали своей монументальностью. Математические умения позволили Пифагору выявить закономерность в самой форме пирамиды Хеопса. Увиденное им, стало прообразом египетского треугольника и его знаменитой теоремы, что послужит универсальным инструментом для строительства сооружений с правильными во всех соотношениях углами.

Окунувшись немного в математику, приходит понимание, что свойства чудо-фигуры подчиняются аксиоме (истине) – в прямоугольном треугольнике сумма квадратов катетов равна сумме квадрата гипотенузы (теорема Пифагора),

Путем вычислений находим ответ – длина гипотенузы равна 5.

Если подставить по аналогии другие значения, например, a=2, b=3 или a=6, b=7, то гипотенуза уже не будет равна 4 или 8, в этом и есть уникальность египетского треугольника со сторонами 3, 4, 5.

Подводя итог сказанному, теперь понятно, как древним египтянам удавалось так точно и выверено строить одно из семи чудес света.

О египетском треугольнике и его свойствах хорошо известно ещё с древних времён. Эта фигура широко применялась в строительстве для разметки и построения правильных углов.

История египетского треугольника

Создателем этой геометрической конструкции является один из величайших математиков древности Пифагор. Именно благодаря его математическим изысканиям мы можем в полной мере использовать все свойства данного геометрического построения в строительстве.

Важно! Принято считать, что толчком к открытию этой геометрической фигуры послужило путешествие Пифагора в Африку, где он увидел египетские пирамиды. Возможно, именно они стали прообразом данной конструкции.

Можно предположить, что математические навыки позволили Пифагору заметить закономерность в формах строения. Дальнейшее развитие событий можно легко представить. Базовый анализ и построение выводов создали одну из самых значимых фигур в истории. Скорее всего, в качестве прообраза была выбрана именно пирамида Хеопса из-за своих практически совершенных пропорций.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Важно! Конечно, в идеале лучшим вариантом будет использование транспортира или угольника.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

1. 5,
2. 4,
3. 3.

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Внимание! Свойства египетского треугольника таковы, что квадрат гипотенузы равен квадратам двух катетов.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Внимание! Длина каждого отрезка составит 4 и 3 см (при минимальных значениях). Пересечение этих прямых образует прямой угол, равняющийся 90 градусам.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Важно! Для получения нужного наклона вырвите лист бумаги из журнала и согните его. При этом линии изгиба будут проходить через угол. Края должны совпасть.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Внимание! Соотношение сторон на 30º нужно, чтобы сделать шестиугольники. Их свойства востребованы в столярных заготовках.

Итоги

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.

ПРАВИЛО ВЕРЁВКИ ИЛИ ЕГИПЕТСКИЙ ТРЕУГОЛЬНИК

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

ВВЕДЕНИЕ

Из различных источников информации мы узнали, что древние египтяне более 4000 лет назад умели строить прямые углы на земле после разлива Нила. Для этого они изобрели специальный прибор и умело им пользовались. Эту работу выполняли особые люди –геометры – землемеры, гарпедонапты.

В настоящее время прямые углы строятся новыми, современными способами. Но возникает вопрос: сумели бы мы сегодня построить прямые углы так, как это делали в древнем мире, применим ли древний способ сегодня? В нахождении ответа на этот вопрос заключается актуальность исследования.

Объект исследования. Построение прямого угла.

Предмет исследования. Способы построения прямого угла.

Гипотеза: Выполнив работу мы узнаем древние и современные способы построения прямого угла в различных ситуациях, сравним эти способы и сделаем соответствующий вывод о практической значимости этих способов.

Цель работы: установить и сравнить способы построения прямого угла в Древнем Египте и современные способы построения прямого угла на бумаге и на местности.

Задачи исследования:

1.Собрать информацию о построении прямого угла на бумаге и на местности в школьных учебниках, справочниках, Интернет – ресурсах.

2. Установить :

причины необходимости построения прямого угла в Древнем Египте;

какие инструменты применялись в Египте для построения геометрических построений на больших площадях;

кто такие гарпедонапты;

правило веревки;

кто автор конструкции «3:4:5»

3. Провести эксперимент построения прямого угла с помощью веревки с 12 узлами.

4. Установить примеры применения правила веревки в настоящее время.

Методы исследования:

Анализ учебников, справочной математической литературы.

Построения с помощью циркуля и линейки.

Компьютерное моделирование математических объектов с помощью ИГС GeoGebra.

Анализ, сравнение, сопоставление и обобщение объектов, полученных в результате моделирования, проверка выдвинутых гипотез.

Аналитические рассуждения.

ОСНОВНАЯ ЧАСТЬ

Правило верёвки или египетский треугольник

1. Построение прямого угла в тетради и н местности

В современном мире люди постоянно сталкиваются с решением геометрических задач и мало кто задумывается, что решением таких задач занимались еще тысячи лет назад .

Одной из таких задач является построение прямого угла. На уроках математики, начиная с 3-го класса нам приходится изображать прямой угол в тетради. Для этого мы пользуемся чертежным треугольником, соблюдая определенные правила (Приложение 1). Умеем строить прямые углы по клеточкам в тетради, строить прямой угол с помощью транспортира. А если нет под рукой угольника, транспортира и бумага без клеточек, можно любой лист бумаги перегнуть два раза, и прямой угол готов.(Приложение 1). Специалисты прямые углы на земельных участках строят с помощью специальных приборов экера и астролябии. Созданоптический измерительный прибор – теодолит, при помощи которого с высокой точностью выполняются измерения и построения вертикальных и горизонтальных углов (Приложение 2).

Экер представляет собой два бруска, расположенных под прямым углом и укреплённых на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Такой прибор можно сделать в школьных мастерских и даже дома.

Чтобы построить прямой угол на местности  с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (прямая ОВ на рисунке).

 2.Практическая необходимость построения прямых углов в древности

Необходимость построения прямых углов возникла в древние времена за сотни лет до нашей эры. После разлива рек нужно было восстановить прежние границы земельных участков. Построения на земле выполнялись с помощью циркуля и линейки – это древнейшие способы в евклидовой геометрии, известные со времен Древней Греции. При строительстве пирамид нужно было уметь построить прямые углы в вертикальной плоскости, что делалось с помощью огромных прямоугольных треугольников. Это был тяжелый труд. Затрачивалось много времени и сил. Уже в те далекие времена был изобретен угол – измеритель.

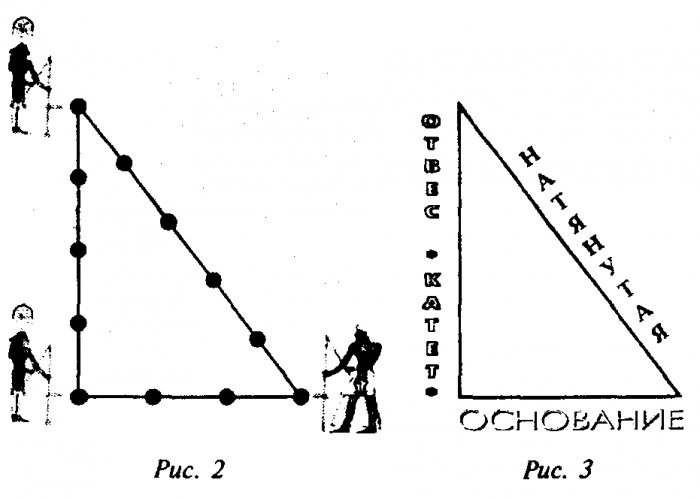
На рисунке изображены древние египтяне – землемеры, гарпедонапты. Именно они по преданиям выработали практическую геометрию при обмерах земельных участков и фундаментов строений.

Единственным рабочим инструментом у них была веревка с узлами. Для построения прямого угла они отмеряли 3,4 и 5 узлов, при этом получался прямой угол.

3.Египетский треугольник

В истории математики не найдено фактов более раннего применения приспособления для построения прямых углов на местности, поэтому его называют египетским треугольником. Придумали подобный способ замеров не древние египтяне, как могло бы показаться, судя по названию. На самом деле таким методом разметки пользовались строители ещё задолго до появления пирамид. Суть метода заключается в том, чтобы разделить квадрат будущего строения на два одинаковых треугольника со сторонами, относящимися друг к другу как 3:4:5. В Древнем Египте числа 3, 4, 5, 12 считались священными. В священном египетском треугольнике отношение сторон равно 3 : 4 : 5, сумма всех чисел равняется 12 – самому популярному числу всех времен и народов.

Интересно, что до древнего Египта, таким способом строили в Китае, Вавилоне, Месопотамии.

4.Практическое применение «правила веревки»

В древнейшие времена египтяне, приступая к постройке пирамиды, дворца или обыкновенного дома, сначала отмечали направление сторон горизонта (это очень важно, так как освещенность в строении зависит от положения его окон и дверей по отношению к солнцу). Действовали они следующим образом. Для того чтобы найти направление север – юг, втыкали вертикально палку и следили за ее тенью. Она становилась наименьшей, когда ее конец указывал на север. Этот треугольник, полученный из замкнутой веревки с 12 узлами, древние египтяне использовали для ориентации по частям света. Направление на юг определялось самой короткой за день тенью от вертикальной палки. От ее основания откладывали 3 узла на север, тогда 4 узла показывали на восток.

«Правило веревки» использовали для построения алтарей, которые по священному предписанию должны были иметь строгую ориентацию четырех сторон горизонта, а так же при строительстве великих храмов в Египте, Вавилоне, Китае и в Мексике.

5.Еще один способ построения прямых углов в Древнем Египте

Такой способ построения прямого угла на земле трудоемок, но в школьных тетрадях вполне можно строить перпендикулярные прямые таким способом. Обоснование этого способа мы делаем на уроках геометрии при изучение взаимного расположения двух окружностей.

6. Применение правила веревки в современных задачах

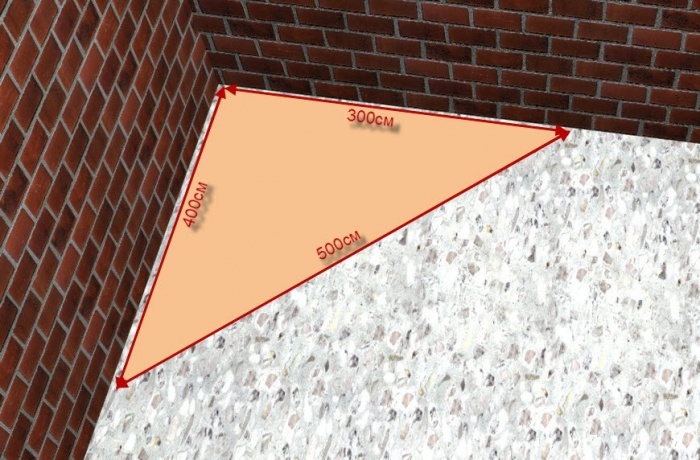
Египетский треугольник широко использовался в строительстве более 2,5 веков. И сегодня иногда приходится применять данную методику, при отсутствии необходимых инструментов, чтобы получить прямые углы. Свойства этой фигуры уникальны, что гарантирует точность в архитектуре и строительстве, без которой не обойтись Строительство с применением египетского треугольника – древний способ, но он активно используемый до сих пор современными строителями. Например при разметке фундамента для дома, при разметке дачного участка . (Приложение ).

ЗАКЛЮЧЕНИЕ

Выполнив работу мы восстановили историю построения прямого угла от “Правила веревки” – с помощь треугольника, отношение сторон которого 3:4:5, до построения прямого угла в настоящее время с помощью современных инструментов в тетради (прямоугольного треугольника, циркуля, линейки) и приборов, которые применяются на земельных участках: экера ( применяется и на школьных площадках, и на дачных участках, отличается простотой изготовления), специальные приборы – астролябии и оптический прибор – теодолит, которые применяются при строительстве различных объектов, при планировки дорог, предприятий, дачных поселков. Убедились в том, что “Правило веревки” может применяться в некоторых случаях и в сегодняшней практике.

ВЫВОДЫ

Гипотеза работы подтвердилась, цель и задачи выполнены.

Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметки полей, при создании архитектурных шедевров, существовали специальные люди, которые применяли геометрические правила.

Во многих исторических письменах имеются следы, что уникальные свойства “египетского треугольника” были известны и широко использовались за много веков до Пифагора и не только в Египте, но и далеко за его пределами: в Месопотамии, в древнем Китае, в Вавилоне.

В настоящее время существуют специальные инструменты и приборы для построения прямого угла в тетради, на доске, на участке земли, но старинный способ построения прямого угла «правило веревки» может применяться и сегодня, причем отношения сторон могут выражаться пифагоровыми тройками чисел.

ИСТОЧНИКИ ИНФОРМАЦИИ

Глейзер Г.И. «История математики в школе VII – VIII кл. Пособие для учителей.. – М: «Просвещение»,1983г. – 240с.;

Рыбников К.А. «Возникновение и развитие математической науки». Книга для учителя.- М: «Просвещение», 1967г. – 159с.

 «Энциклопедическом словаре юного математика», сост. Савин А.П. –М: «Педагогика»,1989г.-352с.;

Интернет – источники

Египетский треугольник и качества… domsdetat.ru (дата обращения 12/10/2021);

Египетский треугольник в строительстве – История…… domsdetat.ru (дата обращения 12/10/2021);

Египетский треугольник – любопытные подробности lubopinie.ru (дата обращения 12/10/2021);

Египетский треугольник Пифагора, свойства, углы, стороны dasinok.ru (дата обращения 12/10/2021);

Зачем египетский треугольник был нужен pulse.vail/ru (дата обращения 12.10. 2021);

Приложение 1. Построение прямого угла в тетради

1.Алгоритм построения прямого угла с помощью прямоугольного треугольника

1.Провести луч RС—это одна сторона угла, точка R– его вершина.

2.Расположить чертёжный треугольник так, чтобы его вершина совпала с точкой R и одна из его сторон пошла по лучу RC.

3.Карандашом по второй стороне прямого угла прямоугольника провести вторую сторону прямого угла, обозначить его RN. Угол CRN – прямой.

 2 Можно построить прямой угол по клеточкам в тетради

3. Можно построить прямой угол с помощью транспортира

4.Построение с помощью циркуля

а) Можно построить прямой угол, применив свойство пересечения двух окружностей: прямая, проходящая через точки пересечения двух окружностей, образует прямой угол с прямой, проходящей через центры окружностей.

б) Построить окружность , выбрать любую точку окружности и соединить ее отрезками с концами диаметра окружности. Эти радиусы образуют прямой угол.

Приложение 2. Измерительные приборы для построения прямого угла на местности.

Специалисты прямые углы на земельных участках строят с помощью специальных приборов экера и астролябии. Созданоптический измерительный прибор – теодолит, при помощи которого с высокой точностью выполняются измерения и построения вертикальных и горизонтальных углов.

Простейший прибор -экер

Астролябия -угловой прибор, которм пользовалиь геодезисты, посланные Петром Веиким для геодезической съемки Камчатки и Курильских островов. Предназначен главным образом для измерения горизонтальных углов. Появилась астролябия в III ввеке до нашей эры.

Теодолит

Измерительный прибор для определения горизонтальных и вертикальных углов при топографических съёмках, геодезических работах, в строительстве и т. п.

ПРИЛОЖЕНИЕ 3. Буклет “Правило веревки или египетский треугольник”

ПРИЛОЖЕНИЕ 4. Буклеты “Построение прямого угла в тетради и на местности”

Просмотров работы: 640

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

Свойства[править | править код]

• Особенностью такого треугольника, известной ещё со времён античности, является то, что все три стороны его целочисленны, а по теореме, обратной теореме Пифагора, он прямоуголен.
• Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.
• Радиус вписанной в треугольник окружности равен единице.

История[править | править код]

Название треугольнику с таким отношением сторон дали эллины: в VII—V веках до нашей эры древнегреческие философы и математики совершали путешествия в Египет. Так, например, Пифагор в 535 году до нашей эры по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно решение задачи по удвоению площади квадрата с помощью построения на его диагонали большего квадрата привело Пифагора к доказательству знаменитой теоремы. Второй квадрат содержит четыре «половинки» первого, следовательно, его площадь вдвое больше. Эта задача легла в основу характерного для античного искусства способа пропорционирования. Такой способ гармонизации пропорций описал древнегреческий философ Платон (ок. 427—347 гг. до н. э.)^[1].

Такой же приём, если верить Плинию Старшему (23—79 гг. н. э.) и Марку Теренцию Варрону (116—27 гг. до н. э.), использовал знаменитый древнегреческий скульптор Поликлет из Аргоса в сочинении «Канон» (сочинение не сохранилось)^[2].

Египетский треугольник в истории архитектуры[править | править код]

Древнегреческие архитекторы называли строителей египетских пирамид «гарпедонавтами» («натягивателями верёвок» от др.-греч. αρπεδονη — аркан, петля), поскольку они использовали для построения исходной фигуры — прямоугольного треугольника — мерные шнуры. Простейший способ разбивки плана будущего сооружения на земле сводится к построению прямого угла, от которого зависит проецирование центра тяжести будущего сооружения на середину основания — первого условия прочности и надёжности постройки. Древние зодчие решали эту задачу гениально просто. Они брали мерный шнур — верёвку, разделённую узлами на двенадцать равных частей, соединяли её концы (двенадцатый и нулевой узел) и, растягивая на земле, забивали колышки в землю на третьем, седьмом и двенадцатом делениях. При этом получался треугольник с отношениями сторон 3 : 4 : 5 и он при любых размерах будет прямоугольным. Получив прямой угол без всяких вычислений, строители могли его увеличивать до нужных размеров, переносить в вертикальную плоскость. Благодаря своим универсальным свойствам такой треугольник в истории архитектуры получил название: «египетский священный треугольник». Одна из гигантских пирамид в Гизе — пирамида Хефрена — представляет собой в поперечном сечении два «священных треугольника», а отношение высоты к стороне квадратного основания составляет 2:3 (143,5 : 215,25 м). За долгое время эти размеры несколько уменьшились (136,4 : 210,5 м).

Числа треугольника: 3, 4, 5, их сумма 12, а также 7, сумма 3 и 4, — постоянно встречаются в природе и также почитались священными. Согласно религиозным представлениям, универсальная геометрия египетского треугольника олицетворяла Великую триаду богов: Исида и Осирис (два катета) и их сын Гор (гипотенуза). «Бытие и небытие сопоставляются с Исидой и Осирисом, а диагональ с Гором-Соколом» (егип. ḥr — «высота», «небо»)^[3].

Историк и математик Ван дер Варден ставил факт использования египетского треугольника под сомнение, однако более поздние исследования его подтвердили^[4].

Египетский треугольник применяли и в архитектуре средних веков^[5]. Построение треугольника легло в основу средневекового принципа триангуляции (в отличие от квадратуры) при пропорционировании больших кафедральных соборов, причём не только планов и фасадов, но также трифолиев — «трилистников» и иных элементов декора, переплётов окон, резной готический мебели и орнамента типа масверк^[6].

Примечания[править | править код]

См. также[править | править код]

• Пропорционирование
• Теорема Пифагора
• Формула Герона
• Пифагорова тройка