Как найти угол если дано 2 линий

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k ₁ – k ₂ 1 + k ₁· k ₂ = 2 – (-3) 1 + 2·(-3) = 5 -5 = 1

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2 x + 3 y = 0 => y = – 2 3 x ( k ₁ = – 2 3 )

x – 2 3 = y 4 => y = 4 3 x – 8 3 ( k ₂ = 4 3 )

tg γ = k ₁ – k ₂ 1 + k ₁· k ₂ = – 2 3 – 4 3 1 + (- 2 3 )· 4 3 = – 6 3 1 – 8 9 = 18

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

Решение: Так как прямые заданы параметрически, то <2; 1; -1>- направляющий вектор первой прямой, <1; -2; 0>направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.

Преобразуем второе уравнение к каноническому вид.

1 – 3 y = 1 + y -1/3 = y – 1/3 -1/3

3 z – 5 2 = z – 5/3 2/3

Получено уравнение второй прямой в канонической форме

x – 2 -2 = y – 1/3 -1/3 = z – 5/3 2/3

<-2; – 1 3 ; 2 3 >- направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 – 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Упростим и решим:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

Упростим и решим:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Упростим и решим:

Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

m1=αm2, p1=αp2, l1=αl2

(2.7)

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

2. Найти угол между двумя линиями на поверхности в точке их пересечения:
Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле: begin mbox,varphi = displaystylefrac<sqrtcdotsqrt> \ mbox,varphi = displaystylefrac<sqrtcdotsqrt>. end Говорим, что кривая на поверхности $vec=vec(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec=vec_udu+vec_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности: begin S = iintlimits_sqrtdu,dv, end где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой begin I_1=du^2+frac19,mbox^2u,dv^2 end между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии $$ u+v=a, ,, u-v=a,$$ лежащие на поверхности: begin x=u,mboxv, ,, y=u,mbox,v, ,, z=au. end

Решение задачи 2

Первая квадратичная форма данной поверхности: begin I_1=(1+a^2),du^2+u^2,dv^2. end

Данные линии пересекаются в точке: begin left < beginu+v&=a,\ u-v&=a. end right. quad Rightarrow quad P(u=a,v=0). end

Направления данных линий: begin du+dv=0, ,, delta u-delta v=0,, Rightarrow end begin du = -dv, ,, delta u = delta v. end

Задача 3

Дана поверхность: $$z=axy.$$ Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$. Запишем коэффициенты первой квадратичной формы: begin &E=1+(z_x)^2=1+a^2y^2,\ &F=z_xz_y=a^2xy, \ &G=1+(z_y)^2=1+a^2x^2. end

Направления координатных линий: begin &x=x_0 ,, Rightarrow dx=0,\ &y=y_0 ,, Rightarrow delta y=0. end

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

Задача 5 (Феденко 683)

Найти периметр и внутренние углы криволинейного треугольника $$ u=pm av^2/2,,, v=1,$$ расположенного на поверхности $$I_1=du^2+(u^2+a^2)dv^2.$$

Вершины треугольника: begin &A(u=0,, v=0),\ &B(u=-frac<2>,, v=1), \ &C(u=frac<2>,, v=1). end

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника: begin &s_1 = |BC| = a,\ &s_2 = |AC| = frac76 a,\ &s_3 = |BC| = frac76 a,\ &P_<triangle ABC>=s_1+s_2+s_3=frac<10><3>a. end begin &mbox,A = 1, ,, mbox,B=mbox,C=frac23. end

[spoiler title=”источники:”]

http://matworld.ru/analytic-geometry/ugol-mezhdu-prjamymi.php

http://vmath.ru/vf5/diffgeom/seminar8

[/spoiler]

Свойства:     

• накрест лежащие углы равны:    3 = 5, 4 = 6.
• соответственные углы равны:    1 = 5,    4 = 8,     2 = 6,     3 = 7.
• сумма односторонних углов равна 180 градусов:   3 + 6 = 180 градусов,    4 + 5 = 180 градусов.

        

_____________________________________________________________________________________

Теорема    Если две параллельные линии пересекаются третьей (Секущей), тогда выполняется следующее:
ТеоремаТеорема    *      накрест лежащие углы равны   ;
ТеоремаТеорема    *      соответственные углы равны ;
ТеоремаТеорема    *      сумма односторонних углов 180 град. ;
ТеоремаТеорема    *      вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .

_____________________________________________________________________________________

Теорема    Если две прямые перпендикулярны (обе одновременно) к третьей, то они параллельны друг другу.

_____________________________________________________________________________________

Теорема    Если две прямые не параллельны друг другу, то равенства для сумм углов не выполняются:   3 + 6 < 180 ;     4 + 5 > 180 .

_____________________________________________________________________________________

Теорема    Если одна прямая параллельна   второй, а вторая параллельна   третьей, то первая прямая так же параллельна третьей.

_____________________________________________________________________________________

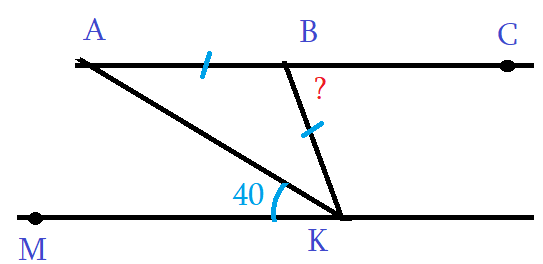
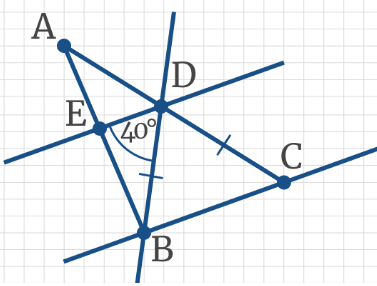
Задача 1:   На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.

• Решение:        АС ║ МК параллельны, АК – секущая, $Rightarrow$   ∠АКМ и ∠КАВ накрест лежащие, $Rightarrow$   ∠КАВ = 40°.
• ∆АВК – равнобедренный, АВ = ВК       $Rightarrow$    углы у основания   ∠КАВ = ∠АКВ значит,   $Rightarrow$   ∠АКВ = 40°.
• Значит, углы   ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность,      ∠МКВ = ∠АКВ + ∠АКМ = 80°.
• АС ║ МК параллельны, АК – секущая, $Rightarrow$   ∠ВКМ и ∠КВС накрест лежащие, $Rightarrow$ Ответ: ∠КВС = 80°.

                 

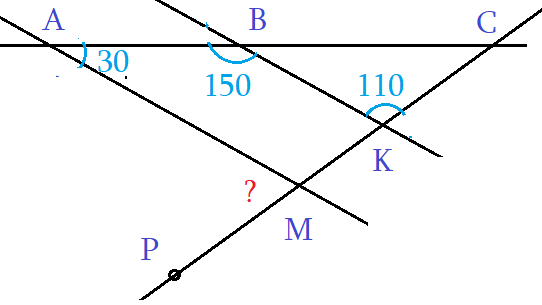
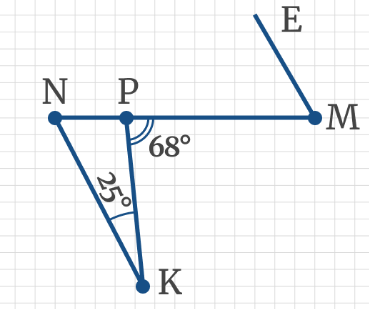
Задача 2:   На рисунке, даны углы ∠ВАМ = 30°,   ∠АВК = 150°,   ∠ВКС = 110°. Найти ∠АМР.

• Решение:     Углы ∠ВАМ и ∠АВК – односторонные от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
• Сумма односторонных 180°? … по теореме “о параллельных”, прямые   АМ и ВК должны быть параллельными. АМ ║ ВК.
• Теперь:    АМ ║ ВК,      СР – секущая. Односторонные углы равные,   ∠ВКС = ∠АМК.       Значит,   ∠АМК = 110°.
• Наконец, углы    ∠АМК и ∠АМР – смежные. Значит,   ∠АМК + ∠АМР = 180°.     $Rightarrow$       ∠АМР = 180° – ∠АМК = 70°.
• Ответ:    ∠АМР = 70°.            Замечание: “надо видеть все секущие к параллельным, и углы к ним”.

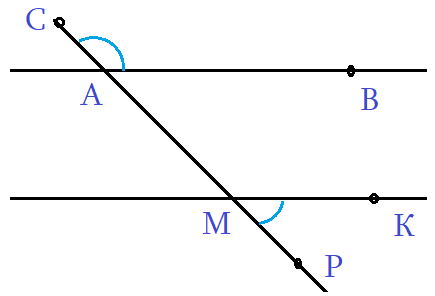
Задача 3:   На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.

• Решение:     Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим:   ∠САВ = 3∠РМК
• Как связаны искомые углы по рисунку?        ∠САВ и ∠МАВ – смежные, значит ∠МАВ = 180° – ∠САВ.
• Углы ∠МАВ и ∠РМК односторонные углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
• Из двух равенств получаем   ∠РМК = 180° – ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим:   ∠РМК = 180° – 3∠РМК
• ∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°.               Ответ:         45°,     135°

     

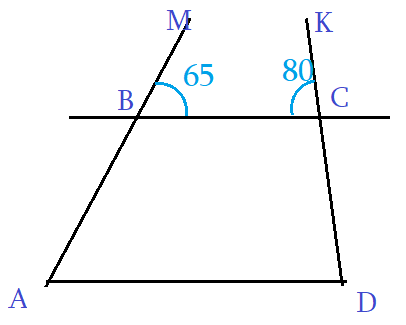
Задача 4:   На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти четырехугольника АВСD.

• Трапеция АВСD:     Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
• Решение:     Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° – ∠МВС = 115°.
• Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° – ∠ВСК = 100°.
• АМ секущая к АD ║ ВС    $Rightarrow$   ∠ВАD и ∠МВС соответственные, значит равные    ∠ВАD = ∠МВС = 65°.
• Аналогично, КD секущая к АD ║ ВС    $Rightarrow$   ∠АDС и ∠ВСК соответственные, значит равные    ∠АDС = ∠ВСК = 80°.
• Ответ:    Углы трапеции   ∠ВАD = 65° ∠АВС = 115°      ∠ВСD = 100°       ∠АDС= 80°

Задача 4, продолжение, “углы в трапеции”:         Пусть углы любые:     ∠МВС = х,    ∠ВСК = у.

• Такими же рассуждениями о смежных и односторонных, получим:    ∠А = х     ∠В = 180° – х    ∠С = 180° – у      ∠D = у
• Видно: ∠А + ∠В = 180°    ∠С + ∠D = 180°.          Сумма углов при боковой стороне трапеции 180° .    Односторонные!
• Видно: ∠А + ∠В + ∠С + ∠D = 180°.            Сумма всех углов трапеции равна 360°. .      Как у четырехугольника?

Факты, Следствия из теорем о углах при параллельных и секущей к ним:

• В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы.         Что секущая?
• В паралеллограмме сумма углов у одной стороны равен 180 град. – внутренные односторонные.     Что секущая?
• В трапеции сумма углов у боковых сторон равен 180 град. – внутренные односторонные. Что секущая?
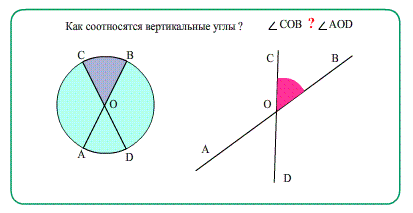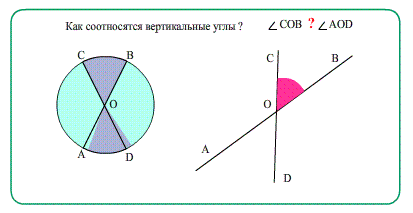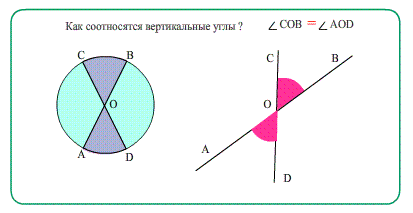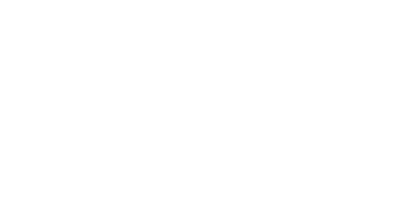
• Еще о углах:          Диаметры в окружности при пересечении образуют равные вертикальные углы.
• Сумма углов треугольника 180 градусов .          Достроить параллельную, увидеть секущую!

Интерактивные Упражнения:

Задачи из сайта https://resh.edu.ru :

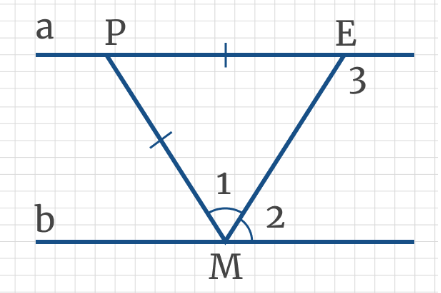
Задача 1:   Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.

                           

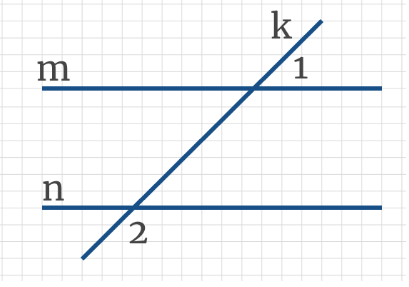
Задача 2:    На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.

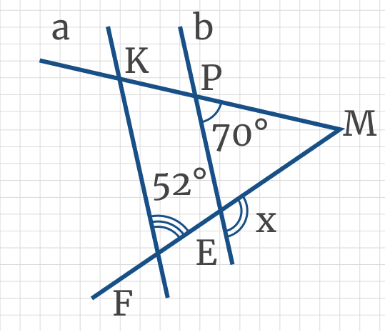
Задача 3:   По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.

                      

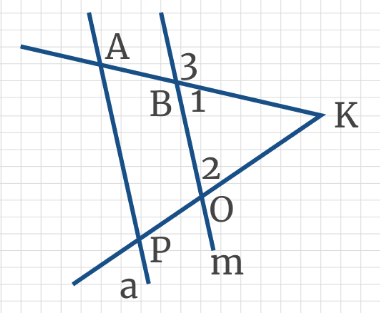
Задача 4:    Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?

Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2   

                       

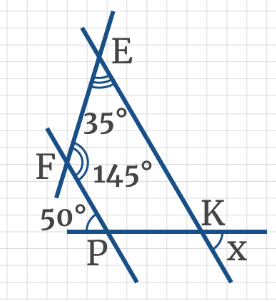
Задача 6:   Прямые FP и EK параллельны, чему равна градусная мера угла x?

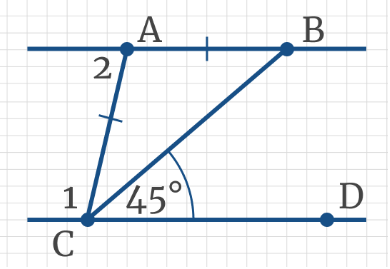
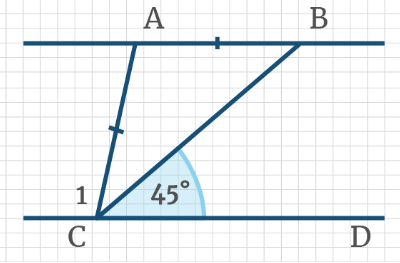
Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.   

                   

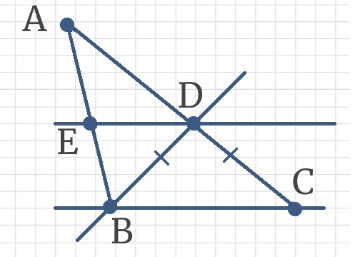
Задача 8:    В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?

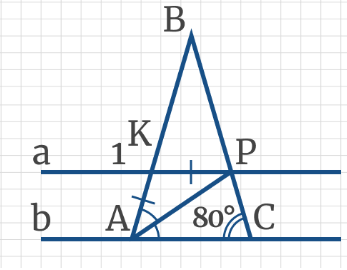
Задача 9:    Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.

                     

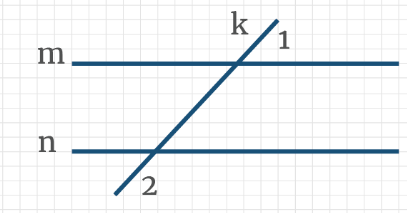
Задача 10:     На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.

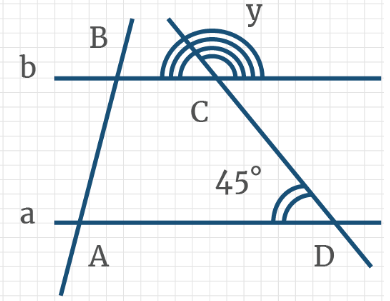
Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.

                      

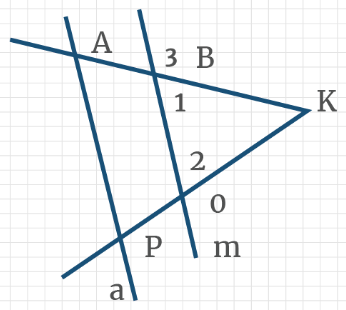
Задача 12:    ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?

Задача 13:   На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.   

                              

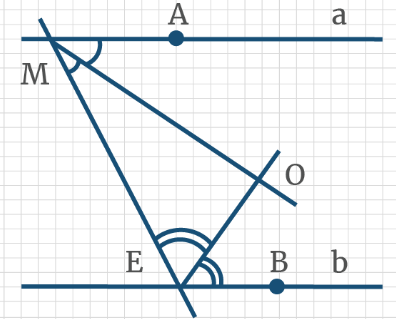
Задача 14:   На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?

Задача 15:   Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?

                                  

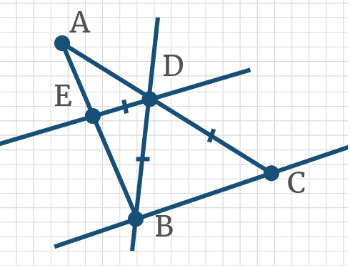
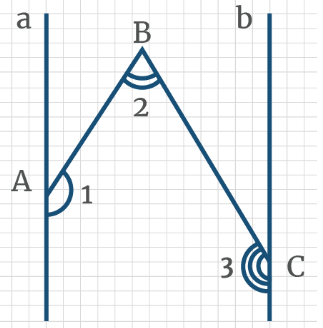
Задача 16:   Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?

Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?   

Задача 18:   Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.

Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.

Задача 20:    “углы в параллелограмме и трапеции”:

1. один из углов параллелограмма 40. найти остальные

2. найти углы параллелограмма, если известно, что сумма двух 80.      (100, 160)

3. найти углы параллелограмма, если известно, что разность двух 70. (110, 130)

4. Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма

5. Углы параллелограмма относятся как 2:3 найти все углы

6. Чему равны углы равнобедренной трапеции, если разность противолежащих 40

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).

Взгляните на рисунок:

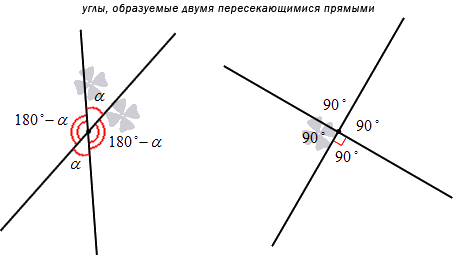
Перейдем к формулированию основного определения.

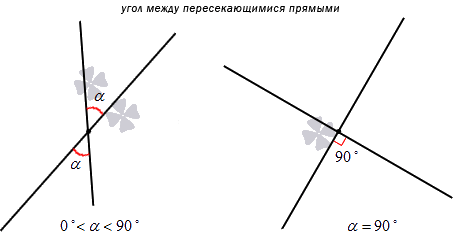
Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.

Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.

Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.

У нас есть прямоугольная (декартова) система координат Oxy, в которой заданы две прямые. Обозначим их буквами a и b. Прямые при этом можно описать с помощью каких-либо уравнений. Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми?

Начнем с формулировки основного принципа нахождения угла в заданных условиях.

Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.

Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:

• угла между направляющими векторами;
• ­угла между нормальными векторами;
• угла между нормальным вектором одной прямой и направляющим вектором другой.

Теперь рассмотрим каждый способ отдельно.

1. Допустим, что у нас есть прямая a с направляющим вектором a→=(ax, ay) и прямая b с направляющим вектором b→(bx, by). Теперь отложим два вектора a→ и b→ от точки пересечения. После этого мы увидим, что они будут располагаться каждый на своей прямой. Тогда у нас есть четыре варианта их взаимного расположения. См. иллюстрацию:

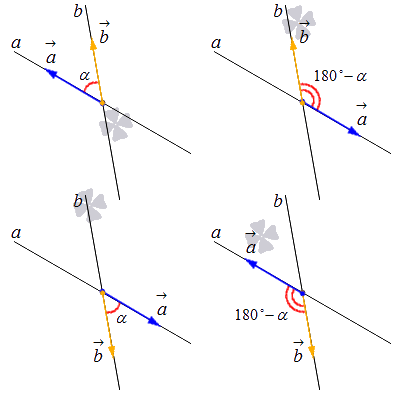
Если угол между двумя векторами не является тупым, то он и будет нужным нам углом между пересекающимися прямыми a и b. Если же он тупой, то искомый угол будет равен углу, смежному с углом a→, b→^. Таким образом, α=a→, b→^ в том случае, если a→, b→^≤90° , и α=180°-a→, b→^, если a→, b→^>90°.

Исходя из того, что косинусы равных углов равны, мы можем переписать получившиеся равенства так: cos α=cos a→, b→^, если a→, b→^≤90°; cos α=cos180°-a→, b→^=-cosa→, b→^, если a→, b→^>90°.

Во втором случае были использованы формулы приведения. Таким образом,

cos αcosa→, b→^, cosa→, b→^≥0-cosa→, b→^, cosa→, b→^<0⇔cos α=cosa→, b→^

Запишем последнюю формулу словами:

Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.

Общий вид формулы косинуса угла между двумя векторами a→=(ax, ay) и b→=(bx, by) выглядит так:

cosa→, b→^=a→, b→^a→·b→=ax·bx+ay·byax2+ay2·bx2+by2

Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:

cos α=ax·bx+ay·byax2+ay2·bx2+by2=ax·bx+ay·byax2+ay2·bx2+by2

Тогда сам угол можно найти по следующей формуле:

α=arccosax·bx+ay+byax2+ay2·bx2+by2

Здесь a→=(ax, ay) и b→=(bx, by) – это направляющие векторы заданных прямых.

Приведем пример решения задачи.

Мы можем решить подобную задачу с помощью нахождения угла между нормальными векторами. Если у нас есть прямая a с нормальным вектором na→=(nax, nay) и прямая b с нормальным вектором nb→=(nbx, nby), то угол между ними будет равен углу между na→ и nb→ либо углу, который будет смежным с na→, nb→^. Этот способ показан на картинке:

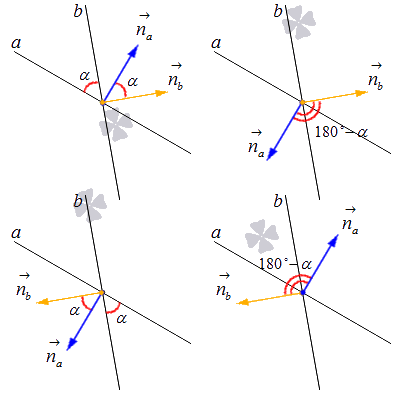
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:

cos α=cosna→, nb→^=nax·nbx+nay+nbynax2+nay2·nbx2+nby2α=arccosnax·nbx+nay+nbynax2+nay2·nbx2+nby2

Здесь na→ и nb→ обозначают нормальные векторы двух заданных прямых.

Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.

Допустим, что прямая a имеет направляющий вектор a→=(ax, ay), а прямая b – нормальный вектор nb→=(nbx, nby). Нам надо отложить эти векторы от точки пересечения и рассмотреть все варианты их взаимного расположения. См. на картинке:

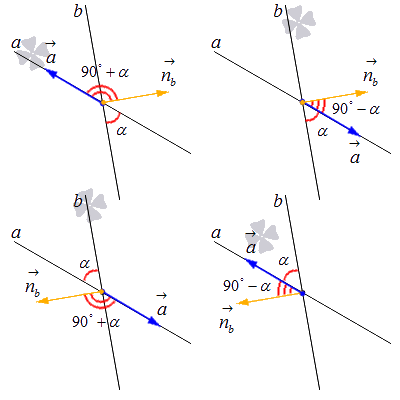
Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.

a→, nb→^=90°-α в том случае, если a→, nb→^≤90°.

Если он менее 90 градусов, то мы получим следующее:

a→, nb→^>90° , тогда a→, nb→^=90°+α

Используя правило равенства косинусов равных углов, запишем:

cosa→, nb→^=cos(90°-α)=sin α при a→, nb→^≤90°.

cosa→, nb→^=cos90°+α=-sin α при a→, nb→^>90°.

Таким образом,

sin α=cosa→, nb→^, a→, nb→^≤90°-cosa→, nb→^, a→, nb→^>90°⇔sin α=cosa→, nb→^, a→, nb→^>0-cosa→, nb→^, a→, nb→^<0⇔⇔sin α=cosa→, nb→^

Сформулируем вывод.

Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.

Запишем необходимые формулы. Нахождение синуса угла:

sin α=cosa→, nb→^=ax·nbx+ay·nbyax2+ay2·nbx2+nby2

Нахождение самого угла:

 α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2

Здесь a→ является направляющим вектором первой прямой, а nb→ – нормальным вектором второй.

Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.

У нас есть прямая a, которая задана в прямоугольной системе координат с помощью уравнения y=k1·x+b1, и прямая b, заданная как y=k2·x+b2. Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:

α=arccosk1·k2+1k12+1·k22+1, гдеk1 и k2 являются угловыми коэффициентами заданных прямых. Для получения этой записи были использованы формулы определения угла через координаты нормальных векторов.

В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.

Как вычислить угол между пересекающимися прямыми в пространстве

Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.

Допустим, что у нас есть прямоугольная система координат, расположенная в трехмерном пространстве. В ней заданы две прямые a и b с точкой пересечения M. Чтобы вычислить координаты направляющих векторов, нам нужно знать уравнения этих прямых. Обозначим направляющие векторы a→=(ax, ay, az) и b→=(bx, by, bz). Для вычисления косинуса угла между ними воспользуемся формулой:

cos α=cosa→, b→^=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2

Для нахождения самого угла нам понадобится эта формула:

α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2

Угол между двумя прямыми

30 мая 2011

Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

Посмотрим, как эта формула работает на конкретных примерах:

Задача. В кубе ABCDA₁B₁C₁D₁ отмечены точки E и F — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AE и BF.

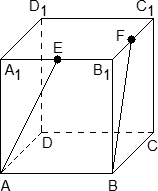
Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.

Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A₁B₁, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).

Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B₁C₁. Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:

Задача. В правильной трехгранной призме ABCA₁B₁C₁, все ребра которой равны 1, отмечены точки D и E — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AD и BE.

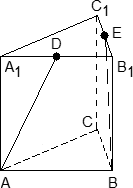
Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA₁. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.

Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A₁B₁. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).

Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C₁B₁ — чуть сложнее. Имеем:

Осталось найти косинус угла:

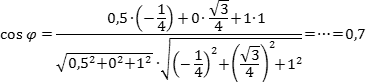
Задача. В правильной шестигранной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 1, отмечены точки K и L — середины ребер A₁B₁ и B₁C₁ соответственно. Найдите угол между прямыми AK и BL.

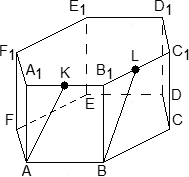
Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:

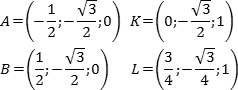
Точки K и L — середины отрезков A₁B₁ и B₁C₁ соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:

Теперь найдем косинус угла:

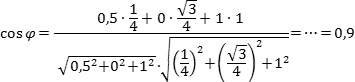
Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.

Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.

Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)

Зная точки, найдем координаты направляющих векторов AE и BF:

Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:

Смотрите также:

1. Задача 14: Угол между плоскостями сечения
2. Видеоурок по задачам C2: расстояние от точки до плоскости
3. Тест к уроку «Что такое логарифм» (средний)
4. Решение задач B12: №440—447
5. Текстовые задачи про рельсы
6. Задача B4: Семья из трех человек едет из Москвы в Нижний Новгород

Когда две непараллельные линии пересекаются, они создают угол между ними. Если линии перпендикулярны, они образуют угол 90 градусов. В противном случае они создают острый, тупой или другой тип угла. Каждый угол имеет «уклон». Например, лестница у стены имеет наклон, значение которого изменяется в зависимости от угла лестницы. Используя небольшую геометрию, вы можете вычислить угол между двумя пересекающимися линиями, определив их наклоны.

Вычислить склоны

Нарисуйте две непараллельные линии на листе миллиметровки. Пометьте линии «Линия А» и «Линия Б.»

Нарисуйте маленький круг в любой точке «Линии А.» Запишите его координаты x и y на миллиметровке и назовите координаты x1 и y1. Предположим, что x1 равен 1, а y1 равен 2.

Нарисуйте еще один маленький круг в другом месте на линии. Запишите координаты и назовите их x2 и y2. Предположим, что x2 равно 3, а y2 равно 4.

Запишите следующее уравнение наклона.

Slope_A = (y2-y1) / (x2-x1)

Подставляя выборочные значения для координат, вы получаете это уравнение:

Slope_A = (4-2) / (3-1)

В этом примере значение Slope_A равно 1.

Повторите эти шаги и вычислите наклон «Линии B.» Маркируйте этот склон “Slope_B.” Для этого примера предположим, что значение для «Slope_B» равно 2.

Вычислить угол

Запишите следующее уравнение:

Tangent_of_Angle = (SlopeB – SlopeA) / (1 + SlopeA * SlopeB)

Выполните расчет. Уравнение выглядит следующим образом с использованием значений, вычисленных в предыдущем разделе:

Tangent_of_Angle = (2-1) / (1 + 1 * 2)

В этом примере значение «Tangent_of_Angle» равно 0, 33.

Используйте таблицу тригонометрии, чтобы найти угол, тангенс которого равен «Tangent_of_Angle», как было вычислено ранее. Если вы посмотрите пример значения 0, 33, вы обнаружите, что соответствующий ему угол, с точностью до десятых градуса, составляет 18 градусов. Угол между «линией A» и «линией B» составляет 18 градусов.

подсказки

• Если у вас нет таблицы тригонометрии, вы можете найти ее в Интернете.