Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы
- Перпендикулярные прямые — определение и свойства
- Правила комбинаторики в задаче B6
- Метод координат в пространстве
- Четырехугольная пирамида: как найти координаты вершин
- Задача B4 про три дороги — стандартная задача на движение
Владимир833
Интересуюсь историей и литературой. · 15 окт 2018
∠1 = 180° – ∠3 (так как они смежные и образуют 180 градусов)
∠1 = 30°
Если ∠1 и ∠2 смежные, то ∠2 =∠3, так как они вертикальные.
Если ∠1 и ∠2 не смежные, то тогда они вертикальные и ∠1=∠2
Ответ:∠1 = 30°; ∠2 = 30° или 150(в зависимости от условия)
10,7 K
Андрей Зубков
26 февраля 2020
угла 3 ? один 150? чо прикол чтоле какойто? 180-150= 30 на два угла.. без длин сторон как ты узнаешь углы.. “американец” штоле?
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Как найти смежный угол
Плоским углом называют фигуру, образованную двумя лучами, исходящими из одной точки. Эта точка называется вершиной угла, а лучи – его сторонами. Если один из лучей продолжить за его начальную точку, то есть сделать прямой линией, то его продолжение образует со вторым лучом еще один угол – он называется смежным. Так как стороны угла равнозначны и продолжить можно любую из них, у каждого угла есть по два смежных.
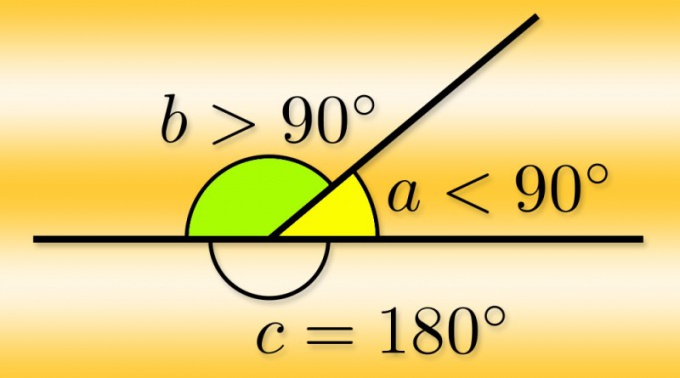
Инструкция
Если вам известна величина основного угла (α) в градусах, рассчитать градусную меру любого из пары смежных (α₁ и α₂) будет очень просто. Каждый из них дополняет основной угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого числа известную величину основного угла α₁ = α₂ = 180°-α.
Величина исходного угла может быть приведена в радианах. Если и результат нужно получить в этих единицах, исходите из того, что развернутому углу соответствует количество радиан, равное числу Пи. Значит, формулу вычисления можно записать в таком виде: α₁ = α₂ = π-α.
Вместо градусной или радианной меры основного угла в условиях может быть дано соотношение величин основного и смежного углов. В этом случае составьте уравнение пропорции. Например, обозначьте через Y величину доли пропорции, относящуюся к основному углу, через X – относящуюся к смежному, а количество градусов, приходящееся на каждую единицу пропорции, обозначьте через k. Тогда общую формулу можно будет записать так: k*X+k*Y=180° или k*(X+Y)=180°. Выразите из нее общий множитель: k=180°/(X+Y). Затем рассчитайте величину смежного угла, умножив полученный коэффициент на долю этого угла в заданной пропорции: k*X = 180°/(X+Y)*X. Например, если это соотношение равно 5/13, величина смежного угла должна составлять 180°/(5+13)*13 = 10°*13 = 130°.
Если в исходных условиях ничего не сказано об основном угле, но дана величина вертикального угла, для вычисления смежных углов используйте формулы двух предыдущих шагов. Согласно определению вертикальный угол образуется двумя лучами, исходящими из той же точки, что и лучи основного угла, но направленными в строго противоположные стороны. Это значит, что градусная или радианная мера основного и вертикального угла равны, а значит, равны и величины смежных им углов.
Видео по теме
Источники:
- как найти смежный угол в треугольнике если
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Лучший ответ
Вахит Вагизович
Высший разум
(375203)
1 день назад
х+х+122= 180
2х= 180-122
х= 58/2= 29°
х+122= 29+151°
Остальные ответы
Artem Zatsepin
Ученик
(191)
6 лет назад
смежный угол=180 градусов, живи с этим
Люля Яресько
Ученик
(192)
6 лет назад
Сумма смежных углов равна 180 градусам.
Найдем самый меньший угол
(180-122)/2=29 градуса
29+122=151 градус – больший угол
Юлия
Знаток
(314)
6 лет назад
Всё просто.
Итак, у нас есть угол 1 и угол 2. Пусть меньший угол, например угол 2, равен х. Тогда угол 1 на 122 градуса больше, значит х+122. Всего – 180 градусов (свойство смежных углов).
И решаем уравнение.
х+х+122=180
2х+122=180
2х=180-122
2х=58
х=29 градусов – это меньший угол 2.
29+122=151 градус – больший угол 1.
Ответ: угол 1 – 151, угол 2 – 29.
Я думаю так. Если хотите, можете поменять обозначения в условии (угол 1 и угол 2). Удачи!
Plyushch DeSanta
Ученик
(164)
4 года назад
х+х+122=180
2х+122=180
2х=180-122
2х=58
х=29 гр. в – это меньший угол 2.
29+122=151 гр. – больший угол 1.
Ответ: угол 1 – 151, угол 2 – 29.
Содержание
- – Как найти угол в равнобедренном треугольнике?
- – Какой угол при основании?
- – Как найти смежный угол в равнобедренном треугольнике?
- – Как найти внешний угол равностороннего треугольника?
- – Что такое угол при вершине?
- – Как найти высоту в равнобедренном треугольнике?
Как найти угол в равнобедренном треугольнике?
Если два угла треугольника равны, такой треугольник является равнобедренным.
…
- В равнобедренном треугольнике углы при основании равны.
- Углы при основании в равнобедренном треугольнике — всегда острые.
- Сумма углов равнобедренного треугольника равна 180 градусам.
Какой угол при основании?
Треугольник называется равнобедренным, если две его стороны равны. Две равные стороны в равнобедренном треугольнике называются боковыми сторонами, а третья сторона – основанием. Свойство углов равнобедренного треугольника. В равнобедренном треугольнике углы при основании равны.
Как найти смежный угол в равнобедренном треугольнике?
д. Смежные углы – два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой. Смежные углы: ∠ A O B и ∠ B O C . Теорема: Сумма смежных углов равна : ∠ A O B + ∠ B O C = 180 ∘ .
Как найти внешний угол равностороннего треугольника?
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. равен половине гипотенузы.
Что такое угол при вершине?
угол при вершине (сверла) — (1.41) Удвоенный угол, образованный осью сверла и проекцией главной режущей кромки на плоскость, проходящую через ось сверла и параллельную этой режущей кромке.
Как найти высоту в равнобедренном треугольнике?
Высота треугольника – это перпендикуляр, который проведен из вершины треугольника к прямой, на которой лежит противолежащая сторона. Высота равнобедренного треугольника вычисляется посредством теоремы Пифагора.
Интересные материалы:
Сколько метров на 1.5 постельное белье?
Сколько метров надо на лестницу?
Сколько метров надо на пододеяльник?
Сколько метров рабицы в рулоне?
Сколько метров тюли нужно на 2 метровый карниз?
Сколько метров ткани на детское постельное белье?
Сколько метров ткани надо на Полутороспальный комплект?
Сколько метров ткани нужно для Двуспального постельного белья?
Сколько метров ткани нужно на детскую кроватку?
Сколько метров ткани нужно на двуспальный комплект?













