Как найти угол если известна медиана

Итак, что нам известно? Треугольник АВС, ВМ – медиана треугольника, ВМ = АМ = СМ. По сути, это – два равнобедренных треугольника с одной общей стороной, ВМ.

Опускаем из М две медианы: на АВ – медиану МК и на ВС – медиану МН. У нас получается четырёхугольник МКВН.

Поскольку в равнобедренных треугольниках медиана является также и высотой, можно сделать вывод, что углы МКВ и МНВ – прямые, их размер составляет 90*. Треугольник АКМ равен треугольнику КМВ, а треугольник МНВ – треугольнику МНС, по двум сторонам и углу между ними: КМ – общая, АК = ВК по условию (не забудем, что МК – медиана!) и углы между ними равны 90* (она же ещё и высота!). То же самое можно сказать и о треугольниках МНВ и МНС -они равны. Значит, равны и углы КАМ и КВМ, с одной стороны, и НВМ и МСН – с другой. Значит, сумма углов КМВ и ВМН равна сумме углов МВК и МВН. А если у четырёхугольника два противоположных угла прямые и ещё два противоположных угла равны, значит, перед нами – прямоугольник, то есть все углы у него – прямые. И угол АВС составляет 90*.

Как найти угол между медианой и стороной

Задача по нахождению угла многоугольника при известных нескольких его параметров достаточно проста. В случае определения угла между медианой треугольника и одной из сторон удобно использовать векторный способ. Для того чтобы задать треугольник, достаточно двух векторов его сторон.

Инструкция

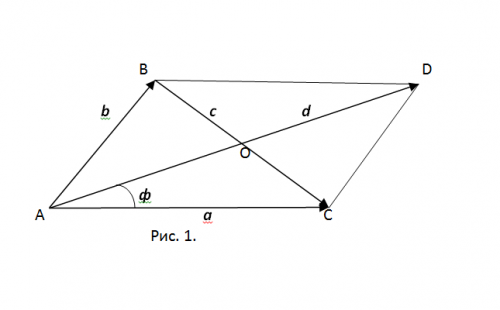
На рис. 1 треугольник достроен до соответствующего ему параллелограмма. При этом известно, что в точке пересечения диагоналей параллелограмма они делятся пополам. Поэтому АО является медианой треугольника АВС, опущенная из А на сторону ВС.
Из этого можно заключить, что необходимо найти угол φ между стороной АС треугольника и медианой АО. Такой же угол, в соответствии с рис. 1, имеется между вектором а и вектором d, соответствующим диагонали параллелограмма AD. По правилу параллелограмма вектор d равен геометрической сумме векторов a и b, d = a + b.

Остается найти способ определения угла φ. Для этого следует использовать скалярное произведение векторов. Скалярное произведение удобнее всего определить на основе тех же векторов a и d, которое определяется по формуле (a, d)= |a||d|cosφ. Здесь φ – угол между векторами a и d. Поскольку скалярное произведение векторов, заданных координатами, определяется выражением:
(a(ax, ay), d(dx, dy))=axdx+aydy, |a|^2= ax^2+ ay^2, |d|^2= dx^2+ dy^2, то
cosφ=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)). Кроме того, сумма векторов в координатной форме определяется выражением: d(dx, dy) = a(ax, ay) + b(bx, by)= {ax+bx, ay+by}, то есть dx= ax+bx, dy=ay+by.

Пример. Треугольник АВС задан векторами a(1,1) и b(2, 5) в соответствии с рис.1. Найти угол φ между его медианой АО и стороной треугольника АС.
Решение. Как уже было показано выше, для этого достаточно найти угол между векторами а и d.
Этот угол задается его косинусом и вычисляется в соответствии со следующим тождеством
cosφ=(axdx+aydy)/(sqrt(ax^2+ ay^2)sqrt(dx^2+ dy^2)).
1. d(dx, dy) = {1+2, 1+5} = d(3, 6).
2. cosφ=(3+6)/(sqrt(1+1)sqrt(9+36))=9/(3sqrt(10))=3/sqrt(10).
φ=arcos(3/sqrt(10)).

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Треугольники общего вида

Треугольники общего вида.

Основные свойства треугольников:

1. Сумма всех углов в треугольнике равна $180°$.
2. В равнобедренном треугольнике углы при основании равны.
3. В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
4. В равностороннем треугольнике все углы по $60°$.
5. Внешний угол треугольника равен сумме двух углов, не смежных с ним.
6. Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ – средняя линия, так как соединяет середины соседних сторон.

Биссектриса – это линия, которая делит угол пополам.

1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
3. Биссектрисы смежных углов перпендикулярны.
4. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.

Медиана – это линия, проведенная из вершины треугольника к середине противоположной стороны.

Свойства медиан:

1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.

2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.

3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.

Высота в треугольнике – это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.

Свойства высот:

1. Три высоты (или их продолжения) пересекаются в одной точке.

2. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.

3. Высоты треугольника обратно пропорциональны его сторонам:

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна 90 градусов.

2. Катет прямоугольного треугольника, лежащий напротив угла в 30 градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

3. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности (R)

4. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.

5. В прямоугольном треугольнике радиус вписанной окружности равен: $r=/<2>$ , где $а$ и $b$ – это катеты, $с$ – гипотенуза.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.

Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$<1>/<2>$	$<√2>/<2>$	$<√3>/<2>$
$cosα$	$<√3>/<2>$	$<√2>/<2>$	$<1>/<2>$
$tgα$	$<√3>/<3>$	$1$	$√3$
$ctgα$	$√3$	$1$	$<√3>/<3>$

Тригонометрические тождества:

1. Основное тригонометрическое тождество:

2. Связь между тангенсом и косинусом одного и того же угла:

3. Связь между котангенсом и синусом одного и того же угла:

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ – коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

1. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
2. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Признаки подобия треугольников:

1. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

В треугольнике $АВС ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Далее подставим числовые данные и найдем $R$

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

[spoiler title=”источники:”]

http://examer.ru/ege_po_matematike/teoriya/treugolniki

[/spoiler]

Геометрия,


вопрос задал marinochkanikitenko,


5 лет назад

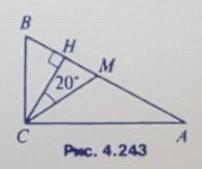
CM-медиана
Найти : угол A, угол B
​

Приложения:

Ответы на вопрос

Ответил elizaburlutskaya

0

треугольник СНМ прямоуг., значит сумма острых углов прямоугольного треугольника равна 90 градусов, следовательно угол СМН=90-20=70. СН-биссектриса угла С=> угол ВСМ=40, а угол В= углу М=70.  По свойству треугольника о сумме углов найдём угол СМА=180-70=110(т.к. смежные), и треугольник СМА равнобедренный, значит угол А=С=(180-110)/2=35.

Ответ: 35, 70.

Ответил marinochkanikitenko

0

Новые вопросы

Как найти угол между медианой и высотой в прямоугольном треугольнике, если известны его острые углы?

Острые углы прямоугольного треугольника равны α и β (β>α). Найти угол между медианой и высотой, проведенными из вершины прямого угла.

Дано: ∆ ABC, ∠C=90º,

CK — медиана,

CF- высота,

∠A=α, ∠B=β, β>α.

Найти: ∠FCK.

Решение:

Так как сумма острых углов прямоугольного треугольника равна 90º, в треугольнике ABC ∠A+∠B=90º, то есть α+β=90º. Значит, β=90º-α.

По свойству прямоугольного треугольника,

   

Следовательно, треугольник ACK- равнобедренный с основанием AC. Отсюда, ∠ACK=∠A=α (как углы при основании равнобедренного треугольника).

Рассмотрим треугольник ACF — прямоугольный (∠CFA=90º, так как CF — высота).

∠A+∠ACF=90º, откуда ∠ACF=90º-∠A=90º-α=β.

∠FCK=∠ACF-∠ACK=β-α.

Вывод: угол между медианой и высотой, проведёнными к гипотенузе, равен разности острых углов прямоугольного треугольника.

Поскольку две другие высоты прямоугольного треугольника совпадают с его катетами, то угол между медианой и высотой, проведённой к катету, есть угол между медианой и другим катетом. Для нахождения этих углов требуются дополнительные данные.

∠CBP — угол между медианой BP и высотой BC

(высота BC является также катетом).

∠CAE — угол между медианой AE и высотой AC

(высота AC является катетом).