Найти угол, зная косинус угла: примеры решения
Евгений Николаевич Беляев
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Имея на руках значение косинуса угла, выяснить угол, которому он принадлежит, совсем не сложно.
Существует специальная тригонометрическая функция, которой можно воспользоваться для этого и называется она арккосинусом (записывается как $arccos$).
Замечание 1
Для того чтобы воспользоваться ей и узнать значение угла, можно применить специальную расширенную таблицу со значениями углов и соответствующих им тригонометрических функций. Эта таблица называется таблицей Брадиса.
Также наиболее часто встречающиеся значения углов и соответствующих им синусов-косинусов собраны в небольшую таблицу внизу:
Рисунок 1. Зная косинус или синус, найти угол. Автор24 — интернет-биржа студенческих работ
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Но есть и другой, более современный вариант нахождения угла по значению косинуса: достаточно включить режим Scientific (Научный) и найти кнопку переключения функций на калькуляторе.
В Windows 10 она обозначается стрелкой как показано на рисунке. При её нажатии кнопка $sin$ поменяется на $sin^{-1}$, а $cos$ на $cos^{-1}$. Теперь для того чтобы узнать значение угла по косинусу — просто набираете значение функции и жмёте кнопку $cos^{-1}$. Не забудьте выбрать нужную единицу измерения — градусы или радианы.
Рисунок 2. Как узнать угол, зная косинус угла. Автор24 — интернет-биржа студенческих работ
Пример 1
Найдите, чему равен $arccos 0,456$.
Решение:
Воспользуемся калькулятором в Научном режиме, на рисунке представлен калькулятор Mac OC, кнопка переключения между $sin$ и $sin^{-1}$ обведена красным:
Рисунок 3. Как по косинусу угла найти угол. Автор24 — интернет-биржа студенческих работ
После нажатия кнопки мы получили значение $α = 27,129°$.
Пример 2
Определите, чему равен угол, если известен его косинус, и он равен $0,95$.
Решение:
Воспользуемся вновь калькулятором и получим, что $α = 18,19°$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 07.05.2023
Арккосинус(y = arccos(x)) – это обратная тригонометрическая функция к косинусу x = cos(y). Область определения -1 ≤ x ≤ 1 и множество значений 0 ≤ y ≤ π.
| arccos(1) = 0° | arccos(-0.5) = 120° | arccos(-0.5) = 240° |
| arccos(0.9998476952) = 1° | arccos(-0.5150380749) = 121° | arccos(-0.4848096202) = 241° |
| arccos(0.999390827) = 2° | arccos(-0.5299192642) = 122° | arccos(-0.4694715628) = 242° |
| arccos(0.9986295348) = 3° | arccos(-0.544639035) = 123° | arccos(-0.4539904997) = 243° |
| arccos(0.9975640503) = 4° | arccos(-0.5591929035) = 124° | arccos(-0.4383711468) = 244° |
| arccos(0.9961946981) = 5° | arccos(-0.5735764364) = 125° | arccos(-0.4226182617) = 245° |
| arccos(0.9945218954) = 6° | arccos(-0.5877852523) = 126° | arccos(-0.4067366431) = 246° |
| arccos(0.9925461516) = 7° | arccos(-0.6018150232) = 127° | arccos(-0.3907311285) = 247° |
| arccos(0.9902680687) = 8° | arccos(-0.6156614753) = 128° | arccos(-0.3746065934) = 248° |
| arccos(0.9876883406) = 9° | arccos(-0.629320391) = 129° | arccos(-0.3583679495) = 249° |
| arccos(0.984807753) = 10° | arccos(-0.6427876097) = 130° | arccos(-0.3420201433) = 250° |
| arccos(0.9816271834) = 11° | arccos(-0.656059029) = 131° | arccos(-0.3255681545) = 251° |
| arccos(0.9781476007) = 12° | arccos(-0.6691306064) = 132° | arccos(-0.3090169944) = 252° |
| arccos(0.9743700648) = 13° | arccos(-0.6819983601) = 133° | arccos(-0.2923717047) = 253° |
| arccos(0.9702957263) = 14° | arccos(-0.6946583705) = 134° | arccos(-0.2756373558) = 254° |
| arccos(0.9659258263) = 15° | arccos(-0.7071067812) = 135° | arccos(-0.2588190451) = 255° |
| arccos(0.9612616959) = 16° | arccos(-0.7193398003) = 136° | arccos(-0.2419218956) = 256° |
| arccos(0.956304756) = 17° | arccos(-0.7313537016) = 137° | arccos(-0.2249510543) = 257° |
| arccos(0.9510565163) = 18° | arccos(-0.7431448255) = 138° | arccos(-0.2079116908) = 258° |
| arccos(0.9455185756) = 19° | arccos(-0.7547095802) = 139° | arccos(-0.1908089954) = 259° |
| arccos(0.9396926208) = 20° | arccos(-0.7660444431) = 140° | arccos(-0.1736481777) = 260° |
| arccos(0.9335804265) = 21° | arccos(-0.7771459615) = 141° | arccos(-0.156434465) = 261° |
| arccos(0.9271838546) = 22° | arccos(-0.7880107536) = 142° | arccos(-0.139173101) = 262° |
| arccos(0.9205048535) = 23° | arccos(-0.79863551) = 143° | arccos(-0.1218693434) = 263° |
| arccos(0.9135454576) = 24° | arccos(-0.8090169944) = 144° | arccos(-0.1045284633) = 264° |
| arccos(0.906307787) = 25° | arccos(-0.8191520443) = 145° | arccos(-0.08715574275) = 265° |
| arccos(0.8987940463) = 26° | arccos(-0.8290375726) = 146° | arccos(-0.06975647374) = 266° |
| arccos(0.8910065242) = 27° | arccos(-0.8386705679) = 147° | arccos(-0.05233595624) = 267° |
| arccos(0.8829475929) = 28° | arccos(-0.8480480962) = 148° | arccos(-0.0348994967) = 268° |
| arccos(0.8746197071) = 29° | arccos(-0.8571673007) = 149° | arccos(-0.01745240644) = 269° |
| arccos(0.8660254038) = 30° | arccos(-0.8660254038) = 150° | arccos(0) = 270° |
| arccos(0.8571673007) = 31° | arccos(-0.8746197071) = 151° | arccos(0.01745240644) = 271° |
| arccos(0.8480480962) = 32° | arccos(-0.8829475929) = 152° | arccos(0.0348994967) = 272° |
| arccos(0.8386705679) = 33° | arccos(-0.8910065242) = 153° | arccos(0.05233595624) = 273° |
| arccos(0.8290375726) = 34° | arccos(-0.8987940463) = 154° | arccos(0.06975647374) = 274° |
| arccos(0.8191520443) = 35° | arccos(-0.906307787) = 155° | arccos(0.08715574275) = 275° |
| arccos(0.8090169944) = 36° | arccos(-0.9135454576) = 156° | arccos(0.1045284633) = 276° |
| arccos(0.79863551) = 37° | arccos(-0.9205048535) = 157° | arccos(0.1218693434) = 277° |
| arccos(0.7880107536) = 38° | arccos(-0.9271838546) = 158° | arccos(0.139173101) = 278° |
| arccos(0.7771459615) = 39° | arccos(-0.9335804265) = 159° | arccos(0.156434465) = 279° |
| arccos(0.7660444431) = 40° | arccos(-0.9396926208) = 160° | arccos(0.1736481777) = 280° |
| arccos(0.7547095802) = 41° | arccos(-0.9455185756) = 161° | arccos(0.1908089954) = 281° |
| arccos(0.7431448255) = 42° | arccos(-0.9510565163) = 162° | arccos(0.2079116908) = 282° |
| arccos(0.7313537016) = 43° | arccos(-0.956304756) = 163° | arccos(0.2249510543) = 283° |
| arccos(0.7193398003) = 44° | arccos(-0.9612616959) = 164° | arccos(0.2419218956) = 284° |
| arccos(0.7071067812) = 45° | arccos(-0.9659258263) = 165° | arccos(0.2588190451) = 285° |
| arccos(0.6946583705) = 46° | arccos(-0.9702957263) = 166° | arccos(0.2756373558) = 286° |
| arccos(0.6819983601) = 47° | arccos(-0.9743700648) = 167° | arccos(0.2923717047) = 287° |
| arccos(0.6691306064) = 48° | arccos(-0.9781476007) = 168° | arccos(0.3090169944) = 288° |
| arccos(0.656059029) = 49° | arccos(-0.9816271834) = 169° | arccos(0.3255681545) = 289° |
| arccos(0.6427876097) = 50° | arccos(-0.984807753) = 170° | arccos(0.3420201433) = 290° |
| arccos(0.629320391) = 51° | arccos(-0.9876883406) = 171° | arccos(0.3583679495) = 291° |
| arccos(0.6156614753) = 52° | arccos(-0.9902680687) = 172° | arccos(0.3746065934) = 292° |
| arccos(0.6018150232) = 53° | arccos(-0.9925461516) = 173° | arccos(0.3907311285) = 293° |
| arccos(0.5877852523) = 54° | arccos(-0.9945218954) = 174° | arccos(0.4067366431) = 294° |
| arccos(0.5735764364) = 55° | arccos(-0.9961946981) = 175° | arccos(0.4226182617) = 295° |
| arccos(0.5591929035) = 56° | arccos(-0.9975640503) = 176° | arccos(0.4383711468) = 296° |
| arccos(0.544639035) = 57° | arccos(-0.9986295348) = 177° | arccos(0.4539904997) = 297° |
| arccos(0.5299192642) = 58° | arccos(-0.999390827) = 178° | arccos(0.4694715628) = 298° |
| arccos(0.5150380749) = 59° | arccos(-0.9998476952) = 179° | arccos(0.4848096202) = 299° |
| arccos(0.5) = 60° | arccos(-1) = 180° | arccos(0.5) = 300° |
| arccos(0.4848096202) = 61° | arccos(-0.9998476952) = 181° | arccos(0.5150380749) = 301° |
| arccos(0.4694715628) = 62° | arccos(-0.999390827) = 182° | arccos(0.5299192642) = 302° |
| arccos(0.4539904997) = 63° | arccos(-0.9986295348) = 183° | arccos(0.544639035) = 303° |
| arccos(0.4383711468) = 64° | arccos(-0.9975640503) = 184° | arccos(0.5591929035) = 304° |
| arccos(0.4226182617) = 65° | arccos(-0.9961946981) = 185° | arccos(0.5735764364) = 305° |
| arccos(0.4067366431) = 66° | arccos(-0.9945218954) = 186° | arccos(0.5877852523) = 306° |
| arccos(0.3907311285) = 67° | arccos(-0.9925461516) = 187° | arccos(0.6018150232) = 307° |
| arccos(0.3746065934) = 68° | arccos(-0.9902680687) = 188° | arccos(0.6156614753) = 308° |
| arccos(0.3583679495) = 69° | arccos(-0.9876883406) = 189° | arccos(0.629320391) = 309° |
| arccos(0.3420201433) = 70° | arccos(-0.984807753) = 190° | arccos(0.6427876097) = 310° |
| arccos(0.3255681545) = 71° | arccos(-0.9816271834) = 191° | arccos(0.656059029) = 311° |
| arccos(0.3090169944) = 72° | arccos(-0.9781476007) = 192° | arccos(0.6691306064) = 312° |
| arccos(0.2923717047) = 73° | arccos(-0.9743700648) = 193° | arccos(0.6819983601) = 313° |
| arccos(0.2756373558) = 74° | arccos(-0.9702957263) = 194° | arccos(0.6946583705) = 314° |
| arccos(0.2588190451) = 75° | arccos(-0.9659258263) = 195° | arccos(0.7071067812) = 315° |
| arccos(0.2419218956) = 76° | arccos(-0.9612616959) = 196° | arccos(0.7193398003) = 316° |
| arccos(0.2249510543) = 77° | arccos(-0.956304756) = 197° | arccos(0.7313537016) = 317° |
| arccos(0.2079116908) = 78° | arccos(-0.9510565163) = 198° | arccos(0.7431448255) = 318° |
| arccos(0.1908089954) = 79° | arccos(-0.9455185756) = 199° | arccos(0.7547095802) = 319° |
| arccos(0.1736481777) = 80° | arccos(-0.9396926208) = 200° | arccos(0.7660444431) = 320° |
| arccos(0.156434465) = 81° | arccos(-0.9335804265) = 201° | arccos(0.7771459615) = 321° |
| arccos(0.139173101) = 82° | arccos(-0.9271838546) = 202° | arccos(0.7880107536) = 322° |
| arccos(0.1218693434) = 83° | arccos(-0.9205048535) = 203° | arccos(0.79863551) = 323° |
| arccos(0.1045284633) = 84° | arccos(-0.9135454576) = 204° | arccos(0.8090169944) = 324° |
| arccos(0.08715574275) = 85° | arccos(-0.906307787) = 205° | arccos(0.8191520443) = 325° |
| arccos(0.06975647374) = 86° | arccos(-0.8987940463) = 206° | arccos(0.8290375726) = 326° |
| arccos(0.05233595624) = 87° | arccos(-0.8910065242) = 207° | arccos(0.8386705679) = 327° |
| arccos(0.0348994967) = 88° | arccos(-0.8829475929) = 208° | arccos(0.8480480962) = 328° |
| arccos(0.01745240644) = 89° | arccos(-0.8746197071) = 209° | arccos(0.8571673007) = 329° |
| arccos(0) = 90° | arccos(-0.8660254038) = 210° | arccos(0.8660254038) = 330° |
| arccos(-0.01745240644) = 91° | arccos(-0.8571673007) = 211° | arccos(0.8746197071) = 331° |
| arccos(-0.0348994967) = 92° | arccos(-0.8480480962) = 212° | arccos(0.8829475929) = 332° |
| arccos(-0.05233595624) = 93° | arccos(-0.8386705679) = 213° | arccos(0.8910065242) = 333° |
| arccos(-0.06975647374) = 94° | arccos(-0.8290375726) = 214° | arccos(0.8987940463) = 334° |
| arccos(-0.08715574275) = 95° | arccos(-0.8191520443) = 215° | arccos(0.906307787) = 335° |
| arccos(-0.1045284633) = 96° | arccos(-0.8090169944) = 216° | arccos(0.9135454576) = 336° |
| arccos(-0.1218693434) = 97° | arccos(-0.79863551) = 217° | arccos(0.9205048535) = 337° |
| arccos(-0.139173101) = 98° | arccos(-0.7880107536) = 218° | arccos(0.9271838546) = 338° |
| arccos(-0.156434465) = 99° | arccos(-0.7771459615) = 219° | arccos(0.9335804265) = 339° |
| arccos(-0.1736481777) = 100° | arccos(-0.7660444431) = 220° | arccos(0.9396926208) = 340° |
| arccos(-0.1908089954) = 101° | arccos(-0.7547095802) = 221° | arccos(0.9455185756) = 341° |
| arccos(-0.2079116908) = 102° | arccos(-0.7431448255) = 222° | arccos(0.9510565163) = 342° |
| arccos(-0.2249510543) = 103° | arccos(-0.7313537016) = 223° | arccos(0.956304756) = 343° |
| arccos(-0.2419218956) = 104° | arccos(-0.7193398003) = 224° | arccos(0.9612616959) = 344° |
| arccos(-0.2588190451) = 105° | arccos(-0.7071067812) = 225° | arccos(0.9659258263) = 345° |
| arccos(-0.2756373558) = 106° | arccos(-0.6946583705) = 226° | arccos(0.9702957263) = 346° |
| arccos(-0.2923717047) = 107° | arccos(-0.6819983601) = 227° | arccos(0.9743700648) = 347° |
| arccos(-0.3090169944) = 108° | arccos(-0.6691306064) = 228° | arccos(0.9781476007) = 348° |
| arccos(-0.3255681545) = 109° | arccos(-0.656059029) = 229° | arccos(0.9816271834) = 349° |
| arccos(-0.3420201433) = 110° | arccos(-0.6427876097) = 230° | arccos(0.984807753) = 350° |
| arccos(-0.3583679495) = 111° | arccos(-0.629320391) = 231° | arccos(0.9876883406) = 351° |
| arccos(-0.3746065934) = 112° | arccos(-0.6156614753) = 232° | arccos(0.9902680687) = 352° |
| arccos(-0.3907311285) = 113° | arccos(-0.6018150232) = 233° | arccos(0.9925461516) = 353° |
| arccos(-0.4067366431) = 114° | arccos(-0.5877852523) = 234° | arccos(0.9945218954) = 354° |
| arccos(-0.4226182617) = 115° | arccos(-0.5735764364) = 235° | arccos(0.9961946981) = 355° |
| arccos(-0.4383711468) = 116° | arccos(-0.5591929035) = 236° | arccos(0.9975640503) = 356° |
| arccos(-0.4539904997) = 117° | arccos(-0.544639035) = 237° | arccos(0.9986295348) = 357° |
| arccos(-0.4694715628) = 118° | arccos(-0.5299192642) = 238° | arccos(0.999390827) = 358° |
| arccos(-0.4848096202) = 119° | arccos(-0.5150380749) = 239° | arccos(0.9998476952) = 359° |
Как найти угол,зная синус либо косинус этого угла?
Знаток
(334),
закрыт
14 лет назад
Наталья
Гений
(53571)
14 лет назад
Для нахождения угла по его синусу, косинусу и т. д. используются так называемые аркфункции: арксинус, арккосинус и т. д. Их обозначают arcsin a, arccos a и т. д.
На Вашем калькуляторе над кнопками с синусом и косинусом есть надписи: sin в степени -1 и cos в степени -1.Это создатели калькулятора так кратко обозначили аркфункции. Чтобы ими воспользоваться, надо набрать число ( например, 0,4965), нажать клавишу SHIFT или 2nd, а затем клавишу, над которой написано cos в степени -1 и равно. У Вас получится угол, косинус которого равен 0,4965.
Понятно?
Sleeper
Знаток
(267)
5 лет назад
Здравствуйте! Я тоже столкнулся с аналогичной проблемой ( учусь программированию языку MQL4), и вот Европа вся сидит на радианах, а нам углы подавай. Вот, я зашел в справочник и там ка-раз все функции в радианах, я сделал свои функции перевода углов в радианы и радианы в углы (они очень просты и не какой сложности), и вот только что написал как по катету и гипотенузе находить косинус, и теперь мне надо найти по косинусу угол, то есть, зная катет и гипотенузу я буду знать угол и наоборот. И хочу использовать в своих расчетах функцию арккосинус которая вернет мне радиану и которую я своей (ранее созданной функцией), переведу в угол. Вот, по ходу и все. Логика понятна?! До свидание. Извините: и совсем не знаю зачем она Вам?! И выпалил, как из пушки – весь свой негатив на Европу. Да будет так – они нам не товарищи. А так я только что был на каком-то сайте и там забиваешь значения и он тебе выводит ответ. Сайты где-то в самом начале поисковиков.
Дмитрий Маштаков
Ученик
(182)
2 года назад
Тут вопрос точности – зная только косинус угла, вы не сможете уверенно вычислить угол, если этот угол маленький. Также и знание синуса вряд ли поможет, если угол близок к 90 градусам. Но если вы знаете одновременно и синус и косинус угла, то
Вот подпрограмма, которая сделает это –
Public Function Usc() As Integer ‘
Dim A As Single, U As Integer
If Abs(Caa) > Abs(Saa) Then
A = Atn(Saa / Caa) * 57.29578
If Caa < 0 Then If Saa > 0 Then A = 180 + A Else A = A – 180
Else: A = Atn(Caa / Saa) * 57.29578
If Saa < 0 Then A = -90 – A Else A = 90 – A
End If: U = A
Usc = U
End Function
‘========
здесь Caa и Saa – косинус и синус, а U это искомое значение угла.
Gras Deus
Профи
(658)
7 месяцев назад
Челу на 2 сообщения выше: хошь прикол? Sin(x)² + Cos(x)² = 1 а знаешь, что это значит? Правильно, это очень простое уравнение, решение которого можно вбить даже в просто компьютер
Как найти угол, если знаешь и синус, и косинус?
МатематикаШколаГеометрия
Владислав Крутиков
22 января 2020 · 5,1 K
ОтветитьУточнить
Mat Mекалль983
22 янв 2020
По знакам синуса и косинуса определяешь, в какой четверти (0-90-180-270-360 градусов) наш угол. Затем, можно хоть арксинус от синуса, хоть арккосинус от косинуса брать (калькулятор, или таблицы). И “разместить” результат в уже найденную четверть. Разумеется угол+_360*i.
4,8 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Как найти угол зная косинус
Кроме прямых тригонометрических функций синус и косинус, существуют и обратные им арксинус и арккосинус. С их помощью можно вычислять величины углов по известным значениям прямых функций. Есть несколько вариантов практической реализации таких расчетов.
Инструкция
Используйте функцию, обратную косинусу (арккосинус) для нахождения угла по известному значению косинуса. Нужное значение арктангенса, а по нему и величину угла, можно найти, например, в «таблицах Брадиса». Бумажные экземпляры этого справочника есть в библиотеках и книжных магазинах, а электронные можно найти в интернете.
Найдите в сети он-лайн калькуляторы для вычисления обратных тригонометрических функций и определите с их помощью нужное значение. Пользоваться такими сервисами намного удобнее, чем искать значения в таблицах. К тому же они могут упростить расчеты, так как многие такие калькуляторы позволяют вычислять не только отдельные значения, но и получать результаты на основе введенных формул, составленных из нескольких операций с тригонометрическими функциями.
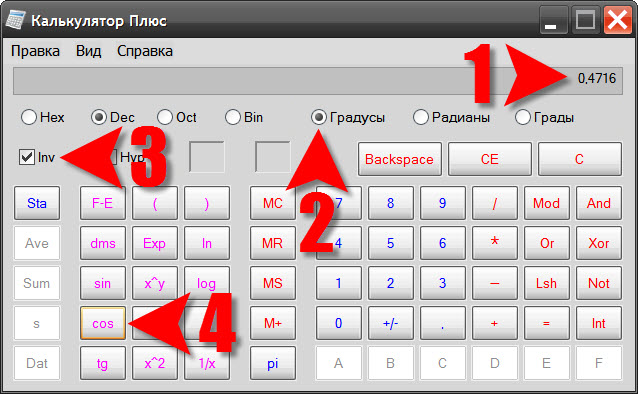
Воспользуйтесь стандартным калькулятором ОС Windows, если хотите обойтись без выхода в интернет. Команда запуска калькулятора помещена в главное меню на кнопке «Пуск». Открыв его, перейдите в раздел «Все программы», затем в подраздел «Стандартные» и щелкните пункт «Калькулятор». По умолчанию он запустится с простейшим интерфейсом, не имеющим инструментов для тригонометрических вычислений. Раскройте в его меню раздел «Вид» и выберите пункт с надписью «Инженерный».
Введите значение косинуса с клавиатуры, или щелкая соответствующие кнопки интерфейса калькулятора. Можно использовать для ввода операции копирования (CTRL + C) и вставки (CTRL + V). Затем выберите единицы измерения, в которых должен быть представлен результат (градусы, радианы или грады) – соответствующий селектор находится строчкой ниже поля ввода числа. После этого надо выставить отметку инвертирования функций в чекбоксе Inv. Этим все приготовления заканчиваются, щелкните кнопку cos и калькулятор рассчитает значение обратной косинусу функции (арккосинус) заданного значения и представит вам результат в выбранных единицах.
Источники:
- как найти значение косинуса если есть угол
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.




