Как найти угол фильм

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

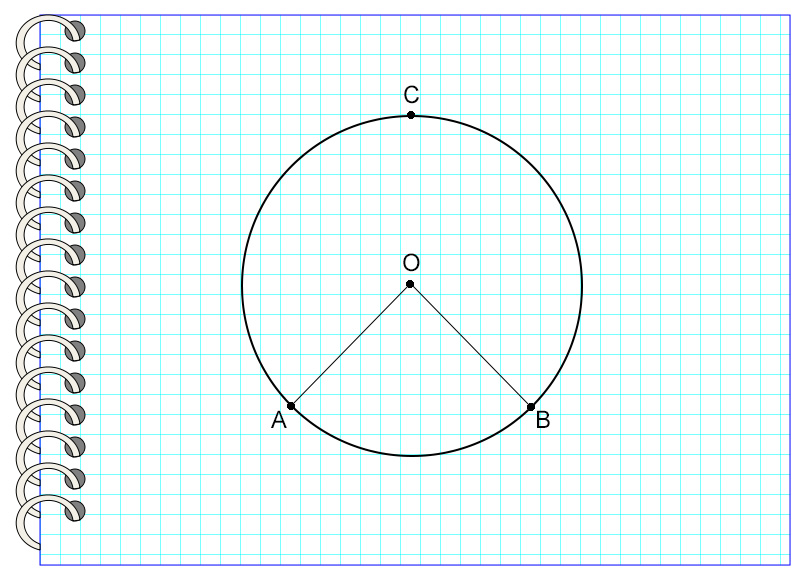
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

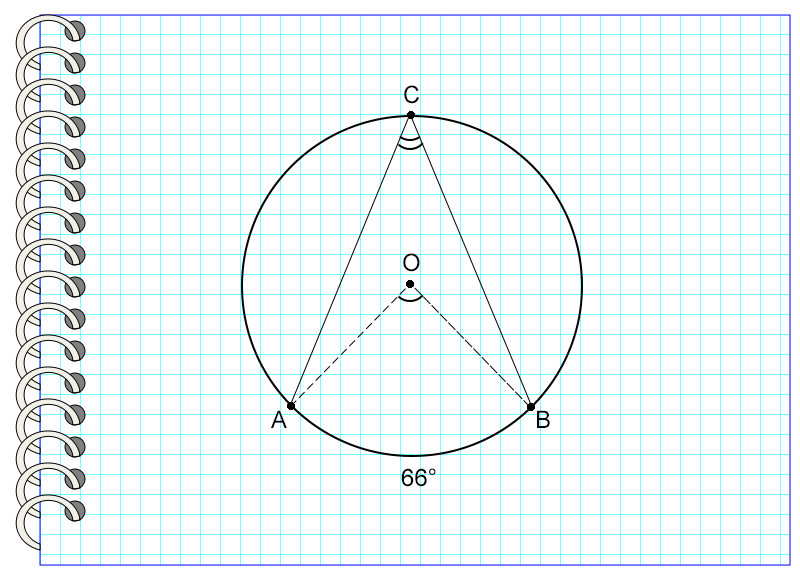
На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

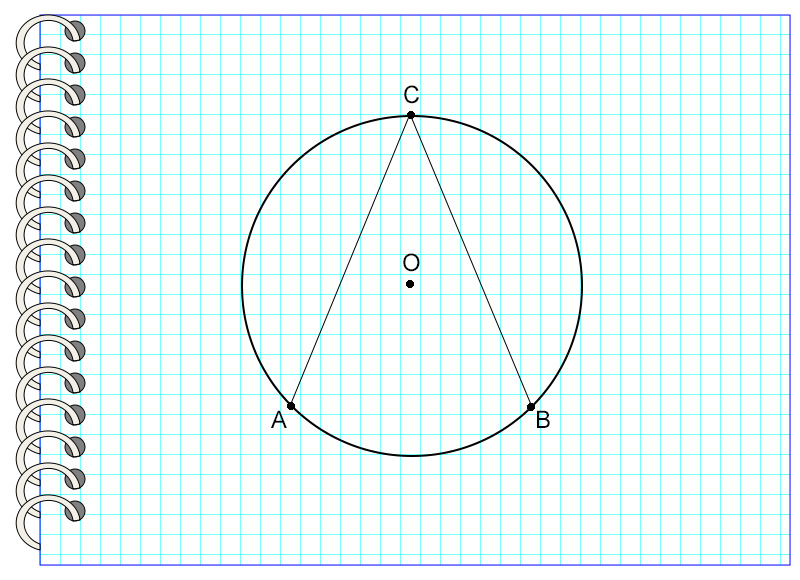
Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

Приведем следующий пример.

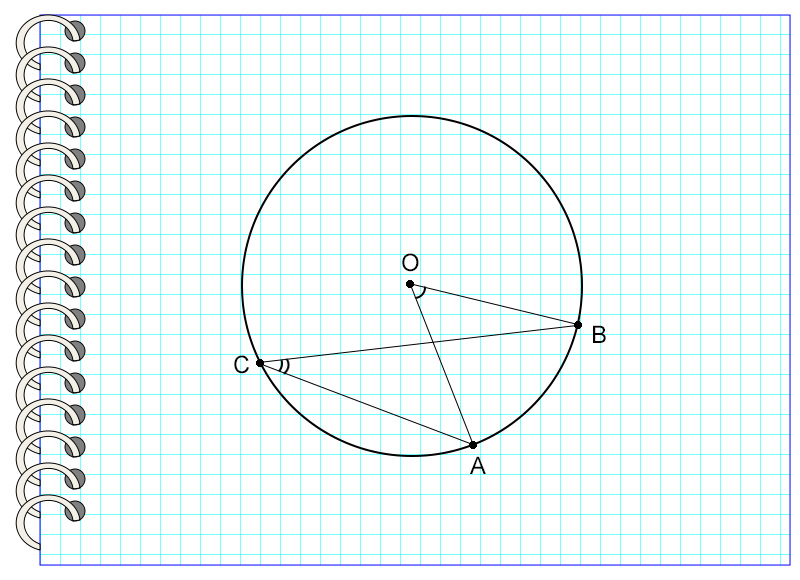
Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

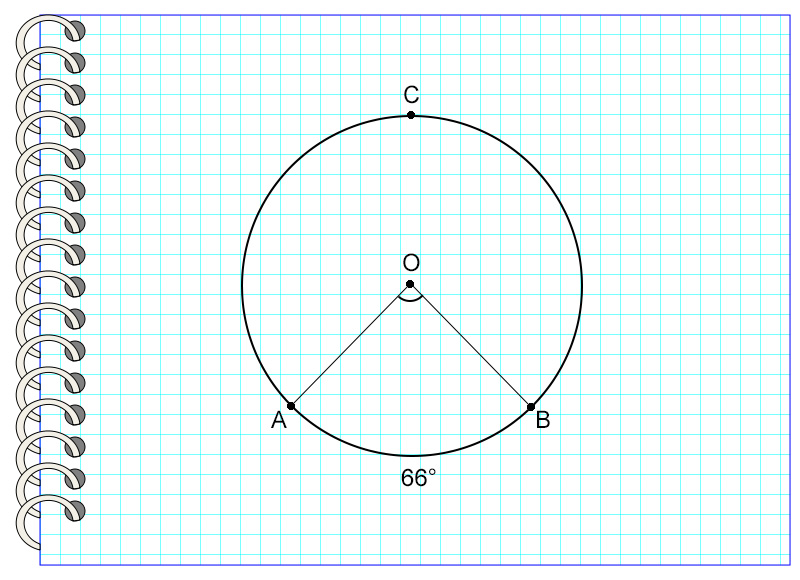
Итак, центральный угол равен градусной мере дуги, на которую он опирается.

На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

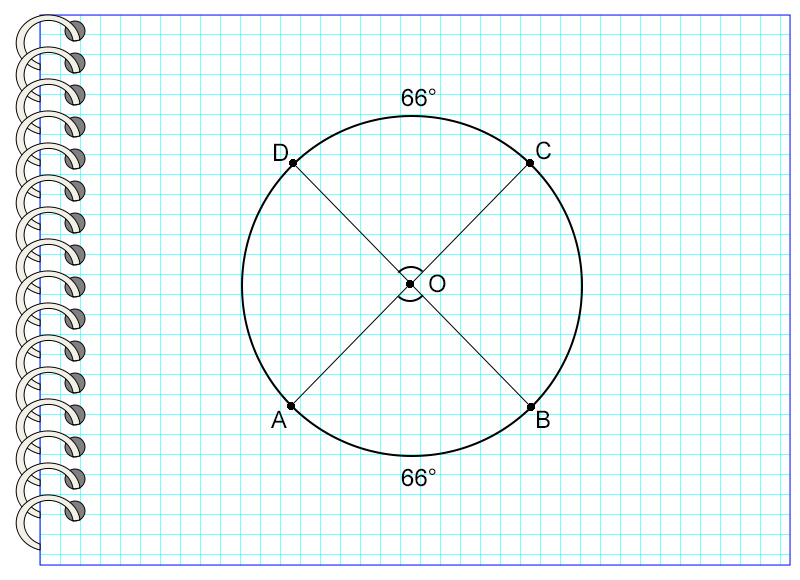
Таким образом, центральные углы, опирающиеся на равные дуги, равны.

На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла – общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

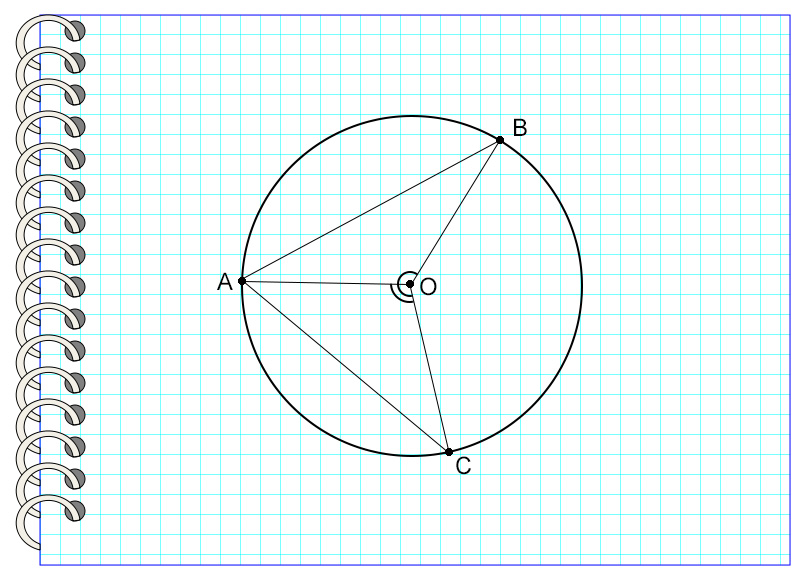
В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° – АС – АВ

ВС = 360° – 120° – 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

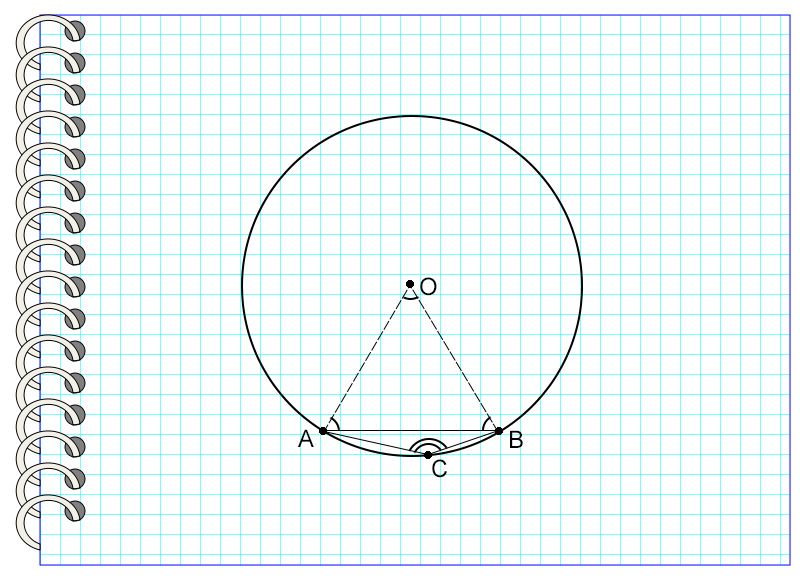
Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° – 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги – 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию – как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° – 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

[spoiler title=”источники:”]

http://fb.ru/article/445770/uglyi-v-okrujnosti-tsentralnyiy-i-vpisannyiy-svoystva-i-sposobyi-nahojdeniya

http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly

[/spoiler]

Правило третей, голландский угол и паралленльный монтаж.

При съёмке фильма операторы руководствуются определёнными правилами, на которые вы не обращаете внимание при просмотре, но тут же заметите, если их проигнорировать. Ведь сделай что-то не так — и зритель запутается, потеряет нить повествования. Сделай в кадре неправильную композицию — зритель не будет знать, на что ему смотреть. Помести в кадре неправильный объект — и он полностью перевернёт смысл происходящего. Вот несколько таких правил.

Правило третей

Правило третей — это такое упрощённое правило «золотого сечения». Суть его заключается в условном разделении кадра на девять равных блоков (3х3, по горизонтали и вертикали). Важные объекты в кадре должны располагаться вдоль разделяющих линий и на точках их пересечения. Такие точки называются «точками интереса».

При взаимодействии персонажей, последние зачастую находятся именно вдоль вертикальных линий. При съёмках природных или городских пейзажей, горизонт припадает на одну из горизонтальных линий. Этого правила придерживаются не только кинематографисты, но и обычные фотографы.

Правило 180 градусов

А это правило позволяет зрителям укладывать происходящее в логически непротиворечивую картину. Правило гласит, что при диалоге двух персонажей камера не должна «залетать» за линию, проходящую между этими персонажами.

Впрочем, правило 180 градусов распространяется не только на диалоги. Если персонаж идет или бежит, то линия — это направление его движения. Если камера «перелетит» через линию, у зрителя создастся впечатление, что персонаж поменял направление и теперь бежит навстречу самому себе. Если персонаж читает, то линия проходит между глазами и книгой. Если в кадре батальная сцена, то один противник должен быть с одной стороны, другой — с другой.

Правило 30 градусов

При смене кадров, камера должна менять угол как минимум на 30 градусов.

Голландский угол

Если вкратце, то голландский угол — это когда в кадре «завален» горизонт. Зачем? Так надо! Это может показать сумасшествие героя, его алкогольное или наркотическое опьянение, конфликт персонажей или просто динамику.

Эффект получается из-за того, что мы, зрители, не смотрим на мир под этим углом, поэтому такой «заваленный» горизонт воспринимается нами как нечто новое, вызывающее своеобразный дискомфорт.

Иногда голландский угол используется для драматизма — при наклоне камеры трагические события и переживания героев воспринимаются острее. А иногда — для подчёркивания царящего вокруг хаоса, ломая заваленным горизонтом всё кадровое пространство.

L-переход и J-переход

Без паники! Сейчас все объясню.

L-переход — это когда кадр меняется, но зритель всё еще слышит звук из предыдущего. Используется приём для того, чтобы лучше ориентировать зрителя в сюжете.

J-переход — это противопоставление L-переходу. В этом случае зритель слышит звук из фрагмента В ещё когда фрагмент А полностью не закончился.

Резкая смена кадра

Такой переход используется, когда необходимо показать серию ключевых кадров с некоторым временным промежутком между ними. Но этот промежуток времени нам не нужен, поэтому мы его вырезаем, оставляя только то, что необходимо для картины.

Переход во время действия

Кадр не обязательно должен сменяться во время логической паузы. Иногда нужно сменить кадр прямо во время действия, чтобы показать это же действие с другой стороны.

Параллельный монтаж

Параллельный монтаж — это несколько сцен, происходящих в один и тот же промежуток времени. Помните «Форсаж 6», когда самолет минут 20 ехал по взлетной полосе? Видимо, авторы хотели применить параллельный монтаж, показать, что несколько сцен происходит в одно и то же время (драка в самолете происходит в то же время, что и погоня кадром спустя). Вышло плохо. Не так, как надо.

Визуальное совпадение

Вы смотрели «Я, снова я и Ирен» с Джимом Керри? Если да, то, должно быть, помните сцену, где… ладно, проще показать, чем описать.

Как вы уже догадались, приём заключается в соединении двух кардинально разных кадров путем какого-либо общего действия, зачастую — движения. Вот другой пример, после него вы сразу поймете, в чём суть.

Взгляд героя

Когда-то режиссёр немого кино Лев Кулешов провёл один интересный эксперимент. Он склеил два кадра, идущих подряд: на первом было лицо человека, смотрящего за кадр, на другом — тарелка супа. При этом зрители были абсолютно уверены, что человек играет голод. Затем режиссёр склеил другие два кадра: на первом было то же самое лицо, что и в первом случае, а на втором — женщина в гробу. На этот раз зрители были уверены, что человек играет не голод, а скорбь.

Зритель привязывает к герою ту эмоцию, которая может возникнуть у последнего, когда он смотрит на тот или иной объект. Смотрит герой на еду — значит, голоден. Смотрит на женщину — значит, с вожделением смотрит, и пускай даже мимика героя не изменилась ни на морщинку.

Аудиовизуальный контрапункт

Впервые я услышал об этом термине на «КиноПоиске». Я даже не уверен, что этот термин не был придуман редакцией, но он всё равно хорош и достоин упоминания.

Кадр в фильме зачастую сопровождается соответствующей мелодией. Если погоня — мелодия быстрая и ритмичная, если главный герой прячется в шкафу от убийцы — щекотливая, а если кто-то лежит на природе и наслаждается умиротворяющими пейзажами — спокойная.

А что, если сделать наоборот? Если расстреливать людей под классику, например. А ведь такая сцена была в «Апокалипсисе сегодня», и никто не скажет, что музыка была ни к месту. Такой приём используется для того, чтобы придать сцене контраста, иронии или юмора, показать отношение героя к действию, которое он совершает.

Фокус

В играх часто встречается такая опция — «Глубина резкости». Суть её заключается в том, что близстоящий объект, на который смотрит игрок, виден чётко, а объекты позади — размыто. Фокус есть в любом из фотоаппаратов, в любом из телефонов — просто откройте камеру на вашем айфоне или нормальном телефоне и сможете сфокусировать тот или иной объект. В кино этим приёмом выделяют ключевой объект в кадре.

Свет

До боли простой приём: зритель подсознательно смотрит на освещённый участок в кадре. Таким образом также выделяются главные объекты композиции.

Насыщенность

Ещё один способ выделения объекта — сделать его насыщенным на блеклом фоне. Смотря фильм, зритель подсознательно обращает внимание на яркие и сочные цвета.

Симметрия

Такое явление как «симметрия» почти не встречается в природе (чур не приводить в пример бабочек и прочих букашек, композицию из них одних не построишь). Именно поэтому она так притягательна для нашего взгляда. Можно найти бесконечно много примеров с симметрией, введя обычный запрос «симметрия в кино» в Google-картинках.

Перспектива

Что такое перспектива? Согласно Гуглу, это «техника изображения пространственных объектов на какой-либо поверхности в соответствии с теми кажущимися сокращениями их размеров, изменениями очертаний формы и светотеневых отношений, которые наблюдаются в натуре». Короче говоря, это чтобы было так, как на картинке снизу.

Правильная перспектива придает кадру объём и глубину. При использовании вышеупомянутых приёмов, можно добиться довольно интересных ракурсов.

Все эти операторские приёмы и создают грамотно поставленное кино, которое может и не блистать гениальным сюжетом, но будет притягивать зрителя своей визуальной составляющей. Засим откланяюсь. Всем хорошего кино!

1. Главная

2. Astro – prorok

3. 
   Как найти угол 90 градусов