A – работа
F – сила
S – путь
a – угол между направлениями движения и силы
Найти
- A
- F
- s
- a
Известно, что:
=
Вычислить ‘A‘
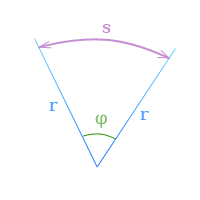
Угловое перемещение (угол поворота) – это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Δφ=φ-φ0
Угловое Δφ перемещения при движении тела по окружности.
Единица измерения угла поворота – 1 радиан [1 рад]. Радиан – это угол, опирающийся на дугу окружности, равную ее радиусу.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Считая, что в начальный момент времени φ0=0, угловое перемещение (угол поворота) часто обозначают φ.
Зная угловую скорость и время, за которое был совершен поворот, можно определить угол поворота:
φ=ωt
Обозначения:
Δφ, φ– угловое перемещение (угол поворота)
Δl – длина дуги
R – радиус окружности
ω – угловая скорость
t – время, за которое был совершен поворот
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
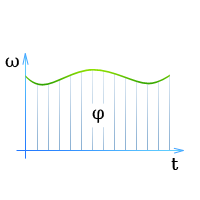
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|
Мы собрали основные формулы по физике с пояснениями в картинках. Более пятидесяти формул, разделенные по категориям физики: кинетика, динамика, статика, молекулярка, термодинамика, электричество, магнетизм, оптика, кинетика. Это не статья, а огромная шпаргалка по физике!
Основные формулы по физике: кинематика, динамика, статика
Итак, как говорится, от элементарного к сложному. Начнём с кинетических формул:
Также давайте вспомним движение по кругу:
Медленно, но уверенно мы перешли более сложной теме – к динамике:
Уже после динамики можно перейти к статике, то есть к условиям равновесия тел относительно оси вращения:
После статики можно рассмотреть и гидростатику:
Куда же без темы “Работа, энергия и мощность”. Именно по ней даются много интересных, но сложных задач. Поэтому без формул здесь не обойтись:
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Основные формулы термодинамики и молекулярной физики
Последняя тема в механике – это “Колебания и волны”:
Теперь можно смело переходить к молекулярной физике:
Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:
Основные формулы электричества
Для многих студентов тема про электричество сложнее, чем про термодинамика, но она не менее важна. Итак, начнём с электростатики:
Переходим к постоянному электрическому току:
Далее добавляем формулы по теме: “Магнитное поле электрического тока”
Электромагнитная индукция тоже важная тема для знания и понимания физики. Конечно, формулы по этой теме необходимы:
Ну и, конечно, куда же без электромагнитных колебаний:
Основные формулы оптической физики
Переходим к следующему разделу по физике – оптика. Здесь даны 8 основных формул, которые необходимо знать. Будьте уверены, задачи по оптике – частое явление:
Основные формулы элементов теории относительности
И последнее, что нужно знать перед экзаменом. Задачи по этой теме попадаются реже, чем предыдущие, но бывают:
Основные формулы световых квантов
Этими формулами приходится часто пользоваться в силу того, что на тему “Световые кванты” попадается немало задач. Итак, рассмотрим их:
На этом можно заканчивать. Конечно, по физике есть ещё огромное количество формул, но они вам не столь не нужны.
Это были основные формулы физики
В статье мы подготовили 50 формул, которые понадобятся на экзамене в 99 случая из 100.
Совет: распечатайте все формулы и возьмите их с собой. Во время печати, вы так или иначе будете смотреть на формулы, запоминая их. К тому же, с основными формулами по физике в кармане, вы будете чувствовать себя на экзамене намного увереннее, чем без них.
Надеемся, что подборка формул вам понравилась!
P.S. Хватило ли вам 50 формул по физике, или статью нужно дополнить? Пишите в комментариях.
Равномерное движение |
|
| S= U∙t, U= S/t, t=S/U | Уравнение движения при равномерном движении?
где U-скорость, t-время, S-расстояние |
| x=x0+U0t | Координата при равномерном прямолинейном движении |
Равномерное движение по окружности |
|
| T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a) |
T – период N – количество оборотов |
| v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t |
v – частота R – радиус окружности |
| ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R) |
ω – угловая скорость t – время |
| υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t |
U – линейная скорость тела |
|
a=υ2/R, a=ω2R, a=Uω |
a – центростремительное ускорение |
| L=φR | L – длина дуги окружности (φ – угол поворота (в радианах)) |
Равноускоренное движение |
|
| X=X0+υ0∙t+(a∙t2)/2 | Уравнение прямолинейного равноускоренного движения |
| S=U0t+a∙t2/2 S= (υ2-υ02) /2а S= (υ+υ0) ∙t /2 = Uср∙t |
Расстояние при равноускоренном движении |
| υ=υ0+a∙t | Rонечная скорость тела при равноускоренном движении |
| a=(υ-υ 0)/t | Ускорение |
| U=√(2gh) tпадения=√(2h/g) S=U∙√(2h/g) |
— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с2, t-время падения, S-расстояние) |
| hmax=U02/2g | Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U0 |
| tподъема=U0/g | Время подъема тела на максимальную высоту |
| tполета=2U0/g | Полное время полета (до возвращения в исходную точку) |
| Sторм=U02/2a | Тормозной путь тела двигавшегося до начала торможения со скоростью U0 , а затем тормозившего с ускорением а |
| U = √(U02+(gt)2) tgβ = Uy/Ux = gt/U0 |
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту |
| hmax=(U0∙sinα)2/2g tподъема=(U0∙sinα)/g |
Бросок с земли на землю под углом к горизонту равным α. Время подъема до высшей точки и максимальная высота |
|
Sx=Ux∙tполета |
Полное время и дальность полета при броске под углом к горизонту |
Импульс |
|
|
p=mυ |
Импульс тела |
|
Ft=∆p |
Импульс силы |
|
F=∆p/∆t |
Второй закон Ньютона в импульсной форме |
|
pk=pn |
Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется |
Энергия |
|
|
A=F∙S∙cosα |
Механическая работа (F – сила, S – путь, – угол между направлением движения и силой) |
|
P=A/t=F∙υ |
Мощность (если мощность переменная, то рассчитывается средняя мощность) |
|
Eп=mgh |
Потенциальная энергия тела, поднятого над землей |
|
Eп=kx2/2 |
Потенциальная энергия упруго деформированного тела |
|
η=Aп/Аз |
Коэффициент полезного действия |
|
Ek=mυ2/2 |
Кинетическая энергия тела |
Молекулярная физика |
|
|
ρ=m/V |
Плотность (ρ – его плотность, m – масса вещества, V – объем) |
|
ν=N/ Na = m/M |
Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса) |
|
М=m/ν |
Молярная масса |
|
m0=m/N=M/Na |
Масса одной молекулы вещества |
|
P=nkT=1/3nm0υ2 |
Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость) |
|
Uкв=√(3kT/m0), Uкв=√(3RT/M) |
Cредняя квадратичная скорость |
|
Ek=3/2∙kT |
Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура) |
|
kNa=R |
Связь универсальной газовой постоянной и постоянной Авогадро |
|
PV=m/M∙RT |
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) |
|
PV=const (m=const и T= const) |
Газовые законы. Закон Бойля-Мариотта (изотермический процесс) |
|
V/T=const (m=const и p= const) |
Газовые законы. Закон Гей-Люссака (изобарный процесс) |
|
P/T =const (m=const и V= const) |
Газовые законы. Закон Шарля (изохорный процесс) |
|
PV/T=const (m=const ) |
Газовые законы. Универсальный газовый закон (Клапейрона) |
|
V=Vo(1+λt) |
Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости) |
|
l=lo(1+αt) |
Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела) |
Динамика |
|
|
Первый закон Ньютона |
Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения |
|
F=ma |
Второй закон Ньютона (F – сила, m – масса, а – ускорение). |
|
F1-2 = — F2-1 |
Третий закон Ньютона (сила действия равна силе противодействия) |
|
Fупр = kx |
Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины) |
|
Fy=-kx |
Закон Гука |
|
Fтр.скольжения=Fтр.макс = μТ |
Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.) |
|
F=mg |
Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел) |
|
gh = GM/(Rn+h)2 = |
Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты) |
|
U = √(GM/(Rn+h)) |
Скорость спутника на круговой орбите радиусом r = Rn + h |
|
U=√(gRn) |
Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты) |
|
T12/T22 = R13/R23 |
Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно |
|
Р=m(g+a) |
Вес тела, движущегося с ускорением а↑ |
Термодинамика |
|
|
Q=cm(T2-T1) |
Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура) |
|
Q=λm |
Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости) |
|
Q=rm |
Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара) |
|
Q=qm |
Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива) |
|
A=P∙ΔV = m/M∙ R∙ΔT, p = const |
Работа идеального газа |
|
U=3/2∙M/µ∙RT |
Внутренняя энергия идеального одноатомного газа |
|
ΔU=A+Q |
Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом) |
|
η= (Q1 — Q2)/ Q1 |
КПД тепловых двигателей |
|
η= (Т1 — Т2)/ Т1 |
КПД идеальных двигателей (цикл Карно) |
|
ρ=pM/RT |
Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура) |
|
φ=ρ/ρ0∙100% |
Относительная влажность (ρ — абсолютная влажность, ρ0 -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре) |
|
Ep = σS |
Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости) |
|
Fн= σL |
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L |
Статика и Гидростатика |
|
|
M=F∙ℓ |
Момент силы (F – сила, ℓ – плечо силы, т.е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы) |
|
Р=F/S |
Давление (F – сила, S – площадь на которую распределено действие силы) |
|
P=ρ∙g∙h |
Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости) |
|
Fa=ρж∙g∙V |
Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости) |
Электростатика |
|
|
q = Ne |
Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд) |
|
λ=q/L, σ=q/S, ρ=q/V |
Линейная, поверхностная и объемная плотность заряда |
|
F=k∙q1∙q2/R2 |
Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε): |
|
E=1/(4πεε0) |
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра |
|
E= σ/(2εε0) |
Напряженность электрического поля, которую создает заряженная плоскость |
|
ε=E0/E |
Диэлектрическая проницаемость |
|
E=F/q |
Напряженность электрического поля |
|
E=k∙q/R2 |
Напряженность электрического поля точечного заряда |
|
E=2πkσ |
Напряженность электрического поля бесконечной плоскости |
|
W= k∙q1q2/R = k∙q1q2/εr |
Потенциальная энергия взаимодействия двух электрических зарядов |
|
U=Ed, Δφ=E∙ Δl |
Cвязь между напряженностью поля и напряжением |
|
A=qU, U=A/q |
Работа электрического поля, Напряжение |
|
A= qEd, U=E∙d |
Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля |
|
φ=W/q |
Потенциал |
|
φ=k∙q/R |
Потенциал точечного заряда |
|
C=q/U |
Электроемкость |
|
C=S∙ε∙ε0/d |
Электроемкость плоского конденсатора |
|
q=CU |
Заряд конденсатора |
|
E = U/d = σ/εε0 |
Напряженность поля внутри конденсатора |
|
F=qE/2 |
Сила притяжения пластин конденсатора |
|
W=qU/2=q²/2С=CU²/2 |
Энергия заряженного конденсатора |
Электрический ток |
|
|
I=q/t |
Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t) |
|
R=ρ∙ℓ/S |
Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника) |
|
R=R0(1+αt) |
Сопротивление проводника |
|
I=U/R |
Закон Ома для участка цепи (U – электрическое напряжение) |
|
I1=I2=I, U1+U2=U, R1+R2=R |
Законы последовательного соединения |
|
U1=U2=U, I1+I2=I, 1/R1+1/R2=1/R |
Законы параллельного соединения |
|
ε=Aст/q |
Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q) |
|
I=ε/(R+r) |
Закон Ома для полной цепи |
|
I=ε/r |
Сила тока короткого замыкания (R=0) |
|
Q=A=I2Rt |
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике |
|
P=IU=U2/R=I2R |
Мощность электрического тока |
|
m = kQ = kIt |
Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит |
Магнетизм |
|
|
Fa=IBℓsinα |
Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля) |
|
M = NBIS∙sinα |
Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции) |
|
Fл=Bqυ∙sinα |
Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля) |
|
R=mU/qB |
Радиус траектории полета заряженной частицы в магнитном поле |
|
B=Fmax/ℓ∙I |
Вектор магнитной индукции |
|
Ф=BSсos α Ф=LI |
Магнитный поток Φ через площадь S |
|
Ei=ΔФ/Δt |
Закон электромагнитной индукции |
|
Ei=Вℓυsinα |
ЭДС индукции при движении проводника |
|
Esi=-L∙ΔI/Δt |
ЭДС самоиндукции |
|
Wм=LI2/2 |
Энергия магнитного поля катушки |
Колебания |
|
|
a+ω02x=0 |
Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0 |
|
x = A cos (ωt + φ0) |
Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний). |
|
Х=Хmax∙cos ωt |
Уравнение гармонических колебаний |
|
T=t/N, v=N/t=1/T |
Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота) |
|
υ = x'(t) = –Aω sin (ωt + φ0) |
Скорость тела при колебательном движении |
|
υm = ωA |
Максимальное (амплитудное) значение скорости |
|
a = υ'(t) = x»(t) |
Ускорение тела при колебательном движении |
|
am = Aω2 |
Максимальное (амплитудное) значение ускорения |
|
ω0=√(g/ℓ) |
Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения) |
|
ω0=√(k/m) |
Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника) |
|
W=CU2/2+LI2/2 |
Электрический контур |
|
T=2π ∙√LC |
Период колебаний кол. контура и циклическая частота |
|
Iд=I0/√2, Iд=Imax/√2 |
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения |
|
P=UдIд =Iд2R=Uд2/R |
Мощность в цепи переменного тока |
|
U1/U2=n1/n2 |
Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2 |
|
λ= υТ=υ/v |
Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота) |
|
XL=ωL=2πLν |
Индуктивное сопротивление |
|
Xc=1/ωC |
Емкостное сопротивление |
|
Z=√(Xc-XL)2+R2 |
Полное сопротивление |
Оптика |
|
|
Lопт=Ln |
Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит) |
|
x=mλL/d |
Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели). |
|
d∙sin φ=k λ |
Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку) |
|
n21=n2/n1= υ 1/ υ 2 |
Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч) |
|
n21=sinα/sinβ |
Показатель преломления |
|
1/F=1/d + 1/f |
Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы) |
|
D=1/F |
Оптическая сила линзы |
|
Δd=kλ, Δd=(2k+1)λ/2 |
max интерференции, min интерференции |
Атомная и ядерная физика |
|
|
E=hv=hc/λ |
Энергия кванта света, т.е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света) |
|
P=mc=h/ λ=Е/с |
Импульс фотона |
|
hν=Aвых+(mU2/2)max |
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (Авых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света) |
|
(mU2/2)max=еUз |
Максимальная кинетическая энергия вылетающих электронов |
|
νк = Aвых/h |
Красная граница фотоэффекта |
|
hνnm = |En – Em| |
Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний |
|
N=N0∙2—t/T |
Закон радиоактивного распада |
|
ECB=(Zmp+Nmn-Mя)∙c2 |
Энергия связи атомных ядер |
Основы СТО |
|
|
ℓ=ℓ0∙√1-υ2/c2 |
Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины |
|
t=t1/√(1-υ2/c2) |
Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета |
|
υ=(υ1+υ2)/1+ υ1∙υ2/c2 |
Релятивистский закон сложения скоростей |
|
Е = mс2 |
Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела) |