Как найти угол гипотенузы онлайн

Как найти углы прямоугольного треугольника

Главная
/
Математика
/
Геометрия
/
Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Прямоугольный треугольник

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

для угла α:

угол β
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

для угла β:

угол α
длины катетов a и b
длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Если ∠β = , то ∠α =

Если ∠α = , то ∠β =

Формула

α = 90° – β

β = 90° – α

Найти углы прямоугольного треугольника зная катеты

Катет a =
Катет b =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2.5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Источник

Если в прямоугольном треугольнике известна гипотенуза и угол α, то можно сразу вычислить катеты и угол β из свойства суммы углов треугольника и отношений синуса и косинуса. (рис. 79.1)
β=90°-α
a=c sin⁡α
b=c cos⁡α

Периметр, заданный суммой катетов и гипотенузы, можно представить в виде суммы известной гипотенузы и выраженных через нее катетов.
P=a+b+c=c sin⁡α+c cos⁡α+c=c(sin⁡α+cos⁡α+1)

Площадь любого прямоугольного треугольника равна половине произведения катетов, следовательно, чтобы рассчитать площадь через гипотенузу и угол α, необходимо также заменить неизвестные на соответствующие выражения.
S=ab/2=(sin⁡α cos⁡α)/2

Треугольник, в котором один угол прямой, будет иметь всего одну высоту, опущенную на гипотенузу. Из любого внутреннего прямоугольного треугольника, полученного с помощью дополнительного построения высоты, можно выразить ее, как произведение катета и синуса угла. (рис. 79.2)
h=b sin⁡α=c cos⁡α sin⁡α

Найти медиану прямоугольного треугольника проще всего, если она опущена на гипотенузу, в таком случае она будет равна ее половине. Медианы катетов вычисляются по стандартным формулам с заменой переменных через гипотенузу. (рис.79.3)
m_с=c/2
m_b=√(2a^2+2c^2-b^2 )/2=√(2a^2+2a^2+2b^2-b^2 )/2=√(4a^2+b^2 )/2=√(4 〖c^2 sin^2〗⁡α+〖c^2 cos^2〗⁡α )/2=(с√(3 sin^2⁡α+1))/2
m_a=√(2c^2+2b^2-a^2 )/2=√(2a^2+2b^2+2b^2-a^2 )/2=√(4 〖c^2 cos〗^2⁡α+sin^2⁡α )/2=(с√(3 cos^2⁡α+1))/2

Рассчитать биссектрисы прямоугольного треугольника тоже достаточно просто, если использовать специальные формулы, зная гипотенузу и угол α. Преобразуя выражения, можно упростить их до следующих тождеств. (рис. 79.4)
l_с=(ab√2)/(a+b)=(c sin⁡α cos⁡α √2)/(sin⁡α+cos⁡α )
l_a=√(bc(a+b+c)(b+c-a) )/(b+c)=√(bc((b+c)^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+c^2-a^2 ) )/(b+c)=√(bc(b^2+2bc+b^2 ) )/(b+c)=√(bc(2b^2+2bc) )/(b+c)=(b√(2c(b+c) ))/(b+c)=(c cos⁡α √(2c(c cos⁡α+c) ))/(c cos⁡α+c)=(c cos⁡α √(2(cos⁡α+1) ))/(cos⁡α+1)
l_b=√(ac(a+b+c)(a+c-b) )/(a+c)=(a√(2c(a+c) ))/(a+c)=(c sin⁡α √(2c(c sin⁡α+c) ))/(c sin⁡α+c)=(c sin⁡α √(2(sin⁡α+1) ))/(sin⁡α+1)

Проведенная средняя линия прямоугольного треугольника создает внутри него еще один подобный треугольник в два раза меньше первоначального, поэтому сама она равна половине параллельной ей стороны. (рис. 79.7)
M_a=a/2=(c sin⁡α)/2
M_b=b/2=(c cos⁡α)/2
M_c=c/2

Прямоугольный треугольник может быть вписан в окружность и описан вокруг нее. Радиус вписанной окружности внутри треугольника можно вычислить, сложив катеты за вычетом гипотенузы, и разделив полученное число на два. Рассчитать радиус описанной окружности для прямоугольного треугольника через гипотенузу еще проще, так как он равен ее половине. (рис. 79.5, 79.6)
r=(a+b-c)/2=(c sin⁡α+c cos⁡α-c)/2=c/2 (sin⁡α+cos⁡α-1)
R=c/2

Источник

Рассчитайте результаты с двух сторон

Рассчитайте результаты с одной стороны и под одним углом

сделано с ❤️

Что такое прямоугольный треугольник?

Прямоугольный треугольник (американский английский) – это треугольник с одним прямым углом (90 °). Он также известен как прямоугольный треугольник (британский английский) или, более формально, ортогональный треугольник.

пример прямоугольного треугольника

Пример прямоугольного треугольника

Что такое калькулятор треугольников?

Треугольники — одна из самых основных фигур в геометрии, и их часто используют для объяснения более сложных фигур. Используя калькулятор треугольников, вы можете легко рассчитать размеры треугольников и решить другие основные математические задачи. Этот простой инструмент может быть полезен, когда вы работаете над домашним заданием или пытаетесь понять более сложную проблему.

Теорема Пифагора

Теорема Пифагора, также известная как теорема Пифагора, связывает три стороны прямоугольного треугольника. Согласно этой формуле, площадь квадрата квадрата, сторона которого является гипотенузой треугольника, равна сумме площадей на двух других сторонах.

См. Визуальную демонстрацию ниже:

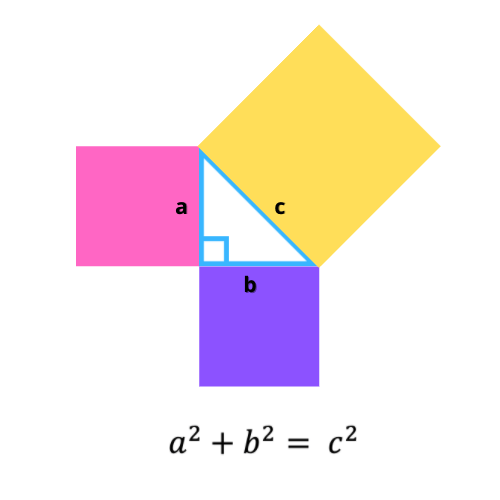
визуализация теоремы пифагора

Теорема Пифагора – Википедия

Формулы прямоугольного треугольника

Прямоугольный треугольник содержит множество полезных формул. Вы можете использовать любую из приведенных ниже формул для вычисления углов, сторон, площади или периметра прямоугольного треугольника. Мы будем ссылаться на треугольник ниже для следующих формул:

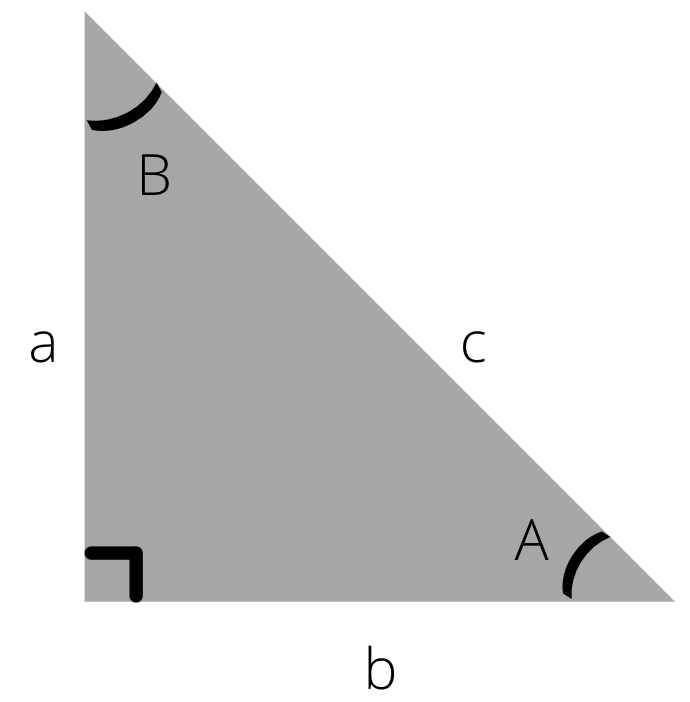
треугольник

Теорема Пифагора

Тригонометрические функции

Площадь треугольника

Периметр треугольника

Также обратите внимание, что вам понадобится следующая таблица при использовании тригонометрических функций:

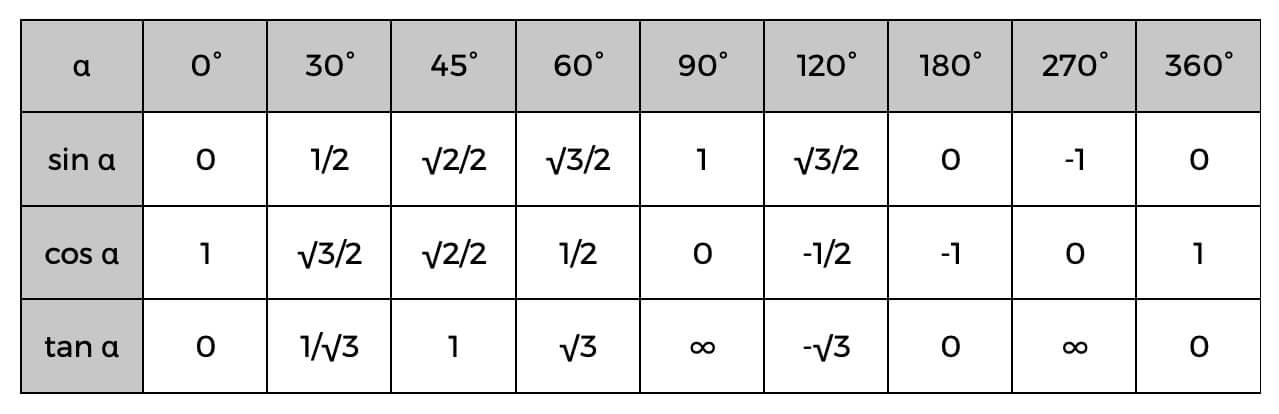
тригонометрическая таблица

Например, если вы используете формулу tan B и рассчитываете, что ее значение равно 1, то, взглянув на таблицу выше, вы узнаете, что значение рассматриваемого угла должно быть 45 °.

Примеры прямоугольного треугольника из повседневной жизни

В прямоугольном треугольнике есть много важных и важных формул, которые используются в математике и в реальной жизни. Ниже вы увидите три наиболее важных использования прямоугольного треугольника:

1) Архитектура и инженерия

Не за горами подумать об использовании прямоугольного треугольника в архитектуре. В основном он используется для расчета длины диагонального соединения, соединяющего две линии. Это используется для расчета диагональной длины ската крыши при проектировании скатной крыши. Вам нужно будет знать только высоту и длину крыши, и все готово!

иллюстрация архитектуры

2) Электроника и электротехника

Правый треугольник используется для решения математических задач в электронике и электротехнике, в первую очередь при проектировании модели. Другой пример важности – внесение эстетических дополнений и обеспечение того, чтобы они не нарушали функцию модели.

Однако прямоугольный треугольник очень удобен при работе со схемами. См. Нижеприведенный наглядный пример для дальнейшей демонстрации и понимания того, как логика прямоугольного треугольника преобразуется в логику схемы.

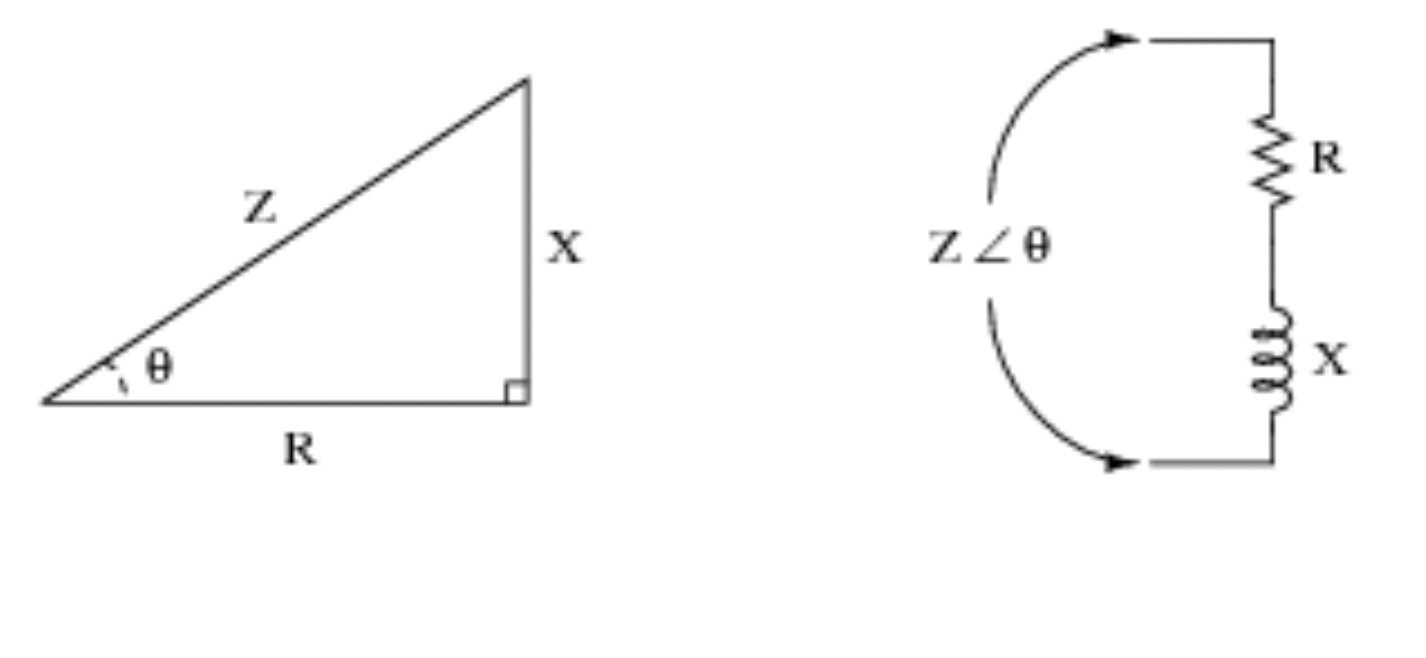
Иллюстрация электроники - изображение от www.learningelectronics.net

3) Землеустройство (гражданское строительство)

Геодезия – это профессия, которая существует уже давно, по крайней мере, столько, сколько показывает история. Это делает геодезист, которому поручено точно измерить поверхность земли в большом масштабе. Вы, наверное, уже догадались об использовании прямоугольного треугольника; в основном, это происходит, когда геодезисту нужно вычислить длину, площади и относительные углы между объектами на ландшафте.

Пример ниже – отличный наглядный демонстратор того, что было объяснено ранее. Геодезист использует соответствующие формулы для расчета своего расстояния от вершины горы или любого другого места, которое он выберет.

иллюстрация гражданского строительства

См. Статью ниже для получения дополнительной информации о том, как работает съемка:

Геодезия – Википедия

Parmis Kazemi

Автор статьи

Parmis Kazemi

Пармис – создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.

Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) русский

Опубликовано: Tue Nov 02 2021

Последнее обновление: Fri Aug 12 2022

В категории Математические калькуляторы

Добавьте Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на свой сайт

Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на других языках

Как добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на мой сайт?

Вы можете легко добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на свой веб-сайт с помощью нашего кода. Вставьте код на свой веб-сайт, и калькулятор автоматически появится на этом месте!

Как добавить виджет Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на сайт WordPress?

Добавить Калькулятор Стороны И Угла Прямоугольного Треугольника (калькулятор Треугольника) на ваш сайт Wordpres быстро и легко! Найдите страницу, на которую вы хотите добавить калькулятор, перейдите в режим редактирования, нажмите «Текст» и вставьте туда код.

Как добавить HTML-виджет на страницу WordPress с помощью нового редактора кодаКак добавить HTML-виджет на страницу WordPress с помощью старого редактора кодаLoading…

Другие математические калькуляторы

Источник

Укажите размеры:

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

β
α

a
b
c

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

tg alpha = dfrac{a}{b}

tg α – тангенс угла α
a – противолежащий катет
b – прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x. Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

angle alpha + angle beta + angle gamma = 180°

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

angle alpha = 90° – angle beta

angle beta = 90° – angle alpha

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла – острые.

Как найти углы прямоугольного треугольника