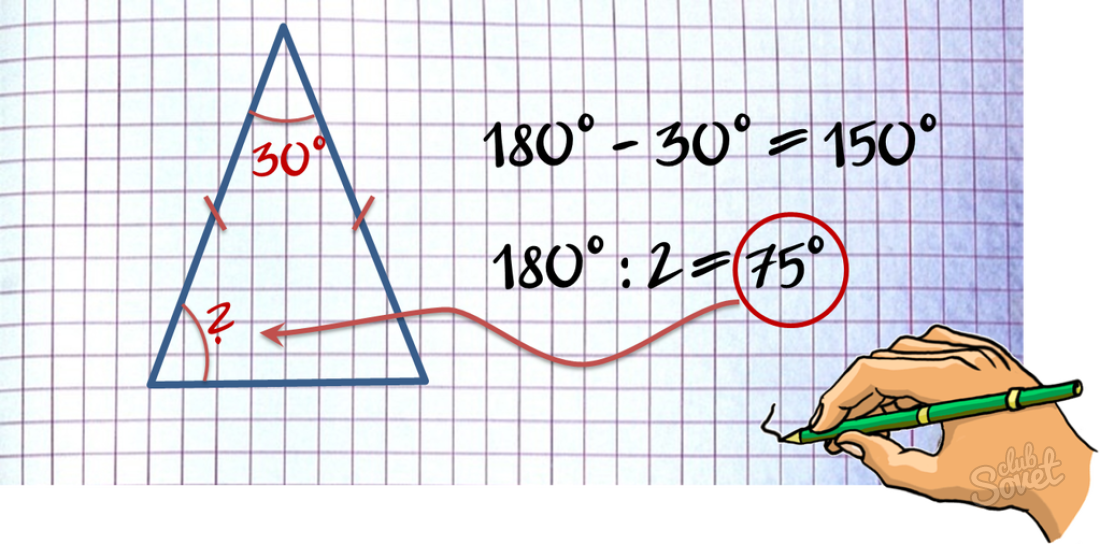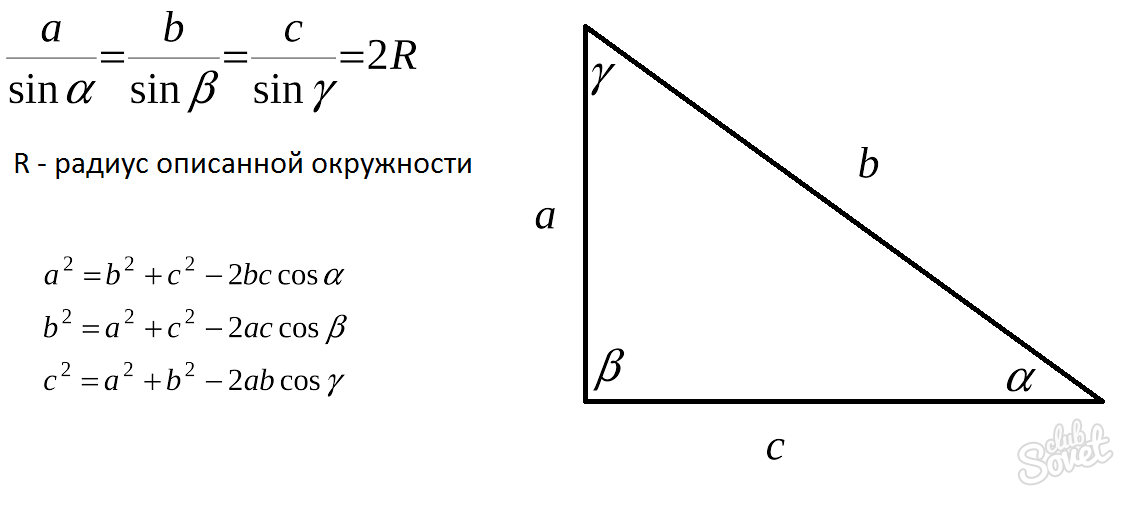Как найти угол гугл

Google Таблицы часто используются для архивирования, доступа и систематизации информации. Но их  также можно использовать для впечатляющих вычислений. Дополнительные сведения об алгоритмах и расчетах Google Таблиц могут дать вам представление о том, как использовать Google для расширенной аналитики и отчетности.

Давайте посмотрим, как найти уклон в Google Таблицах.

«Наклон» — это расчет крутизны линии. Восходящая линия (ниже влево и выше вправо) будет иметь положительный наклон. Нисходящая линия (выше слева и ниже справа) будет иметь отрицательный наклон.

Возможность оценивать и сравнивать наклоны может иметь решающее значение для всего, от научной отчетности до финансовых документов. Тем, кто решает математические задачи, может также потребоваться знать, как найти наклон линии в Google Таблицах.

Начинаем с данных в Google Таблицах

Прежде чем мы сможем найти наклон линии, нам нужно сформировать данные, которые будут создавать линию.

В качестве примера возьмем лист личных финансов. Я записал свои прошлогодние расходы в таблицу, и хотим преобразовать ее в график.

Как видите, данные действительно повсюду. У меня регулярные большие платежи за учебу — поэтому мне сложно увидеть какие-то реальные тенденции. Чтобы я действительно начал видеть тенденции, мне нужно знать, как строить графики.

Как найти уклон в Google Таблицах с помощью диаграммы

Создать диаграмму в Google Таблицах очень просто. Сначала вы выбираете данные, которые хотите превратить в диаграмму, а затем щелкаете значок «Диаграмма» на панели инструментов. На вашем экране появится диаграмма.

Диаграммой немного необычно манипулировать в Google Таблицах, потому что она не является частью структуры ячеек. Его нет в строке или столбце. Скорее, это плавающий объект, который можно перемещать, просто щелкая и перетаскивая.

Но эта линия крайне беспорядочная. Прежде чем мы продолжим, нам нужно сделать четкую линию.

Настройка -> Тип диаграммы -> Точечная диаграмма

Это создает диаграмму рассеяния, а не серию линий.

Настроить -> Серии -> Линия тренда

Это создает единую линию тренда, состоящую из точечной диаграммы. Теперь данные становятся более понятными. Хотя мои расходы поначалу выглядят хаотично, ситуация складывается не так — они только немного увеличиваются.

Теперь у нас есть линия тренда — линия, которую нам нужно использовать, чтобы выяснить, как найти наклон.

На этом этапе можно просто разбить графический калькулятор и определить наклон линии. Но в Google Таблицах есть аналогичная функциональность.

Во-первых, нам нужно определить уравнение, которое Google Таблицы использовали для создания этой линии тренда. Делаем так:

Этикетка -> Использовать уравнение

Мы видим, что используется уравнение 18,2 * x + 1870. Важно отметить, что мы знаем, что наклон равен 18,2.

Как найти уклон в Google Таблицах без диаграммы

Мы также можем найти наклон в Google Таблицах без диаграммы, если нам не нужна вся эта аналитика.

SLOPE ([numerical data], [time data])

Как видите, это дает примерно те же данные, что и наша диаграмма, но в более сложном для восприятия формате. Когда у нас нет диаграммы, сложнее понять наклон, особенно когда данные столь же несопоставимы, как мои данные. Фактически, здесь, без графика, было бы трудно даже увидеть, что график имеет тенденцию к росту с течением времени.

Что можно сделать с уклоном?

Мы знаем, что при таком наклоне, линия растет примерно на 18,20 доллара в месяц. Мы можем видеть, что ситуация имеет тенденцию к росту, и средние значения не указывают на это сами по себе, потому что наклон учитывает то, как диаграмма рассеяния изменяется во времени. Исходя из текущих тенденций, вполне вероятно, что в течение следующего года расходы продолжат расти на эту сумму.

Легче увидеть, были ли данные «проще», хотя простые данные встречаются редко:

Здесь вы можете видеть, что прогрессирование очень простое, а увеличение угла наклона всегда равно 100.

Наклон не дает вам дискретной информации, которую вы можете использовать для определения следующего периода. Скорее, он объединяет все точки данных, которые вы в него вложили, чтобы определить тенденции с течением времени. Это то, что может быть важным во многих отчетах.

Возможно, что более важно, взгляните на следующий пример:

В эту сметную ведомость я внес одно изменение: я снизил расходы на месяц. Теперь мы видим на графике, что наклон идет вниз, и что наклон составляет -3,42. Мы сразу понимаем, что мои расходы снижаются, а не растут.

Основная причина для расчета наклона заключается не только в том, чтобы знать, насколько быстро линия движется вверх или вниз, но и в том, движется ли она вообще вверх или вниз.

Вычисляя наклон без диаграммы, вы можете быстро увидеть, где наблюдаются тенденции данных — без необходимости выполнять какой-либо углубленный анализ.

Однако следует отметить, что наклон расходов не всегда может быть верным. При вычислении информации для отчетов в Google Таблицах качество представленных данных зависит от их качества. Если мои расходы действительно нестабильны, то поведение в прошлом не будет отражать поведение в будущем. Наклоны лучше всего использовать, когда ожидается, что компилируемые данные останутся схожими.

Выводы

В Google Таблицах есть ряд надежных инструментов, которые можно использовать для анализа и построения диаграмм. В этом руководстве вы узнали, как эффективно находить уклон в Google Таблицах.

С помощью передовых методов, таких как наклон, вы можете быстро анализировать данные по определенным факторам, например, определять, идет ли линия вверх или вниз с течением времени. При выполнении этих расчетов вы также можете выбирать между визуальным представлением (например, диаграммами) или просто необработанными числами (с использованием алгоритмов).

Использование этих инструментов позволяет получить более подробные данные, которые можно использовать для получения практических сведений.

Вычисляет тангенс угла (в радианах).

Пример использования

TAN(ПИ())

TAN(A2)

TAN(1)

Синтаксис

TAN(угол)

• угол – угол, тангенс которого необходимо вычислить (в радианах).

См. также:

TANH: Вычисляет гиперболический тангенс вещественного числа.

SINH: Вычисляет гиперболический синус вещественного числа.

SIN: Вычисляет синус угла (в радианах).

РАДИАНЫ: Преобразует величину угла из градусов в радианы.

ПИ: Возвращает число π с точностью до 14 знака после запятой.

ГРАДУСЫ: Преобразует величину угла из радианов в градусы.

COSH: Вычисляет гиперболический косинус вещественного числа.

COS: Вычисляет косинус угла (в радианах).

ATANH: Вычисляет обратный гиперболический тангенс числа (ареатангенс).

ATAN2: Возвращает угол между осью X и линией, проходящей от начала координат (0,0) к точке, обозначенной координатами X и Y. Результат приводится в радианах.

ATAN: Вычисляет арктангенс числа (в радианах).

ASINH: Вычисляет обратный гиперболический синус числа (ареасинус).

ASIN: Вычисляет арксинус числа (в радианах).

ACOSH: Вычисляет обратный гиперболический косинус числа (ареакосинус).

ACOS: Вычисляет арккосинус числа (в радианах).

Примеры

Эта информация оказалась полезной?

Как можно улучшить эту статью?

Тригонометрические функции – синус, косинус и тангенс – основаны на прямоугольном треугольнике (треугольник, содержащий угол, равный 90 градусам).

В математическом классе эти тригонометрические функции находятся с использованием различных тригонометрических соотношений, сравнивающих длину соседних и противоположных сторон треугольника с длиной гипотенузы или друг с другом.

В таблицах Google эти триггерные функции можно найти с помощью функций SIN, COS и TAN для углов, измеренных в радианах .

Степени против радианов

Использование вышеуказанных тригонометрических функций в таблицах Google может быть проще, чем делать это вручную, но, как уже упоминалось, важно понимать, что при использовании этих функций угол необходимо измерять в радианах , а не в градусы – это единица, с которой большинство из нас не знакомо.

Радианы связаны с радиусом круга, причем один радиан приблизительно равен 57 градусам.

Чтобы упростить работу с функциями триггера, используйте функцию РАДИАНЫ Google Spreadsheets, чтобы преобразовать измеряемый угол из градусов в радианы, как показано в ячейке B2 на изображении выше, где угол 30 градусов преобразуется в 0,5235987756 радиан.

Другие варианты для преобразования из градусов в радианы включают в себя:

• вложение функции RADIANS внутрь функции SIN – как показано в строке 3 в примере;
• с помощью PI function Google Spreadsheets в формуле: угол (градусы) * PI ()/180 , как показано в строке 4 в примере.

Синтаксис триггерных функций и аргументы

Синтаксис функции относится к макету функции и включает в себя имя функции, скобки и аргументы.

Синтаксис для функции SIN:

= SIN (угол)

Синтаксис для функции COS:

= COS (угол)

Синтаксис для функции TAN:

= TAN (угол)

угол – вычисляемый угол – измеряется в радианах
– для этого аргумента можно ввести размер угла в радианах или, альтернативно, ссылку ячейки на местоположение этих данных в рабочем листе.

Пример: использование функции SIN Google Spreadsheets

Этот пример охватывает шаги, используемые для ввода функции SIN в ячейку C2 на изображении выше, чтобы найти синус угла 30 градусов или 0,5235987756 радиан.

Те же самые шаги могут использоваться для вычисления косинуса и тангенса для угла, как показано в строках 11 и 12 на изображении выше.

Google Spreadsheets не использует диалоговые окна для ввода аргументов функции, которые можно найти в Excel. Вместо этого у него есть поле auto-offer , которое появляется, когда имя функции вводится в ячейку.

1. Нажмите на ячейку C2, чтобы сделать ее активной ячейкой – здесь будут отображаться результаты функции SIN;
2. Введите знак равенства (=), а затем имя функции sin;
3. По мере ввода появится окно auto-наводить с именами функций, которые начинаются с буквы S;
4. Когда в поле появится имя SIN , щелкните по имени с помощью указателя мыши, чтобы ввести имя функции и открыть круглые или круглые скобки в ячейке C2.

Ввод аргумента функции

Как видно на рисунке выше, аргумент для функции SIN вводится после открытой круглой скобки.

1. Нажмите на ячейку B2 на рабочем листе, чтобы ввести эту ссылку на ячейку в качестве аргумента angle ;
2. Нажмите клавишу Enter на клавиатуре, чтобы ввести закрывающую скобку “) ” после аргумента функции и завершить функцию;
3. Значение 0,5 должно появиться в ячейке C2, которая является синусом угла 30 градусов;
4. Если щелкнуть ячейку C2, полная функция = SIN (B2) появится на панели формул над рабочим листом.

#ЗНАЧЕНИЕ! Ошибки и пустые ячейки

Функция SIN отображает ошибку #VALUE! , если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текст. В пятой строке приведенного выше примера вы можете увидеть это, когда используемая ссылка на ячейку указывает на текстовую метку: Угол (радианы).

Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение (см. Строку шесть выше). Тригонные функции Google Spreadsheets интерпретируют пустые ячейки как ноль, а синус нулевых радиан равен нулю.

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Углы в окружности, центральный и вписанный. Свойства и способы нахождения

Планиметрия – это раздел геометрии, изучающий свойства плоских фигур. К ним относятся не только всем известные треугольники, квадраты, прямоугольники, но и прямые и углы. В планиметрии также существуют такие понятия, как углы в окружности: центральный и вписанный. Но что они означают?

Что такое центральный угол?

Для того чтобы понять, что такое центральный угол, нужно дать определение окружности. Окружность – это совокупность всех точек, равноудаленных от данной точки (центра окружности).

Очень важно отличать ее от круга. Нужно запомнить, что окружность – это замкнутая линия, а круг – это часть плоскости, ограниченная ею. В окружность может быть вписан многоугольник или угол.

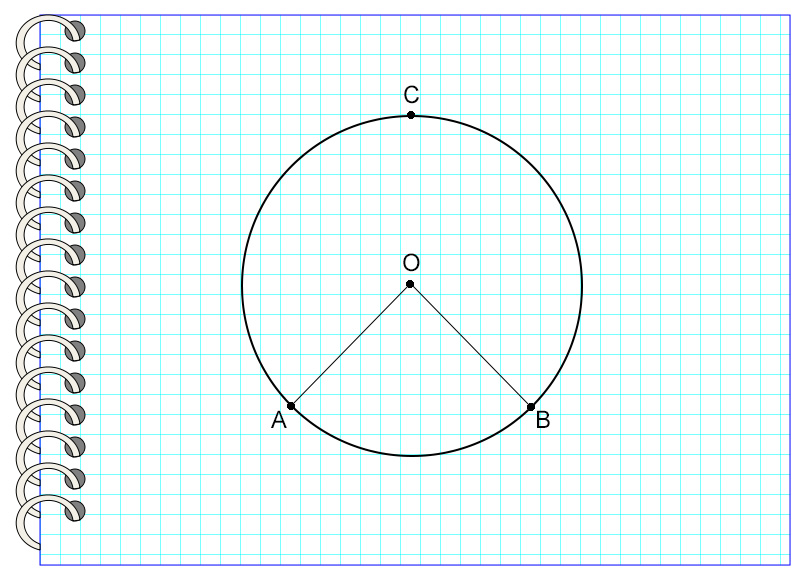
Центральный угол – это такой угол, вершина которого совпадает с центром окружности, а стороны пересекают окружность в двух точках. Дуга, которую угол ограничивает точками пересечения, называется дугой, на которую опирается данный угол.

Рассмотрим пример №1.

На картинке угол AOB – центральный, потому что вершина угла и центр окружности – это одна точка О. Он опирается на дугу AB, не содержащую точку С.

Чем вписанный угол отличается от центрального?

Однако кроме центральных существуют также вписанные углы. В чем же их различие? Так же как и центральный, вписанный в окружность угол опирается на определенную дугу. Но его вершина не совпадает с центром окружности, а лежит на ней.

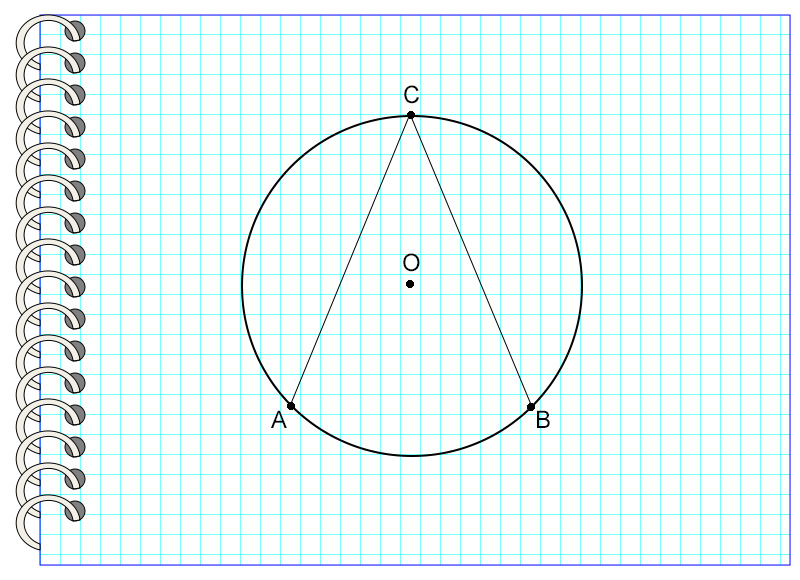
Приведем следующий пример.

Угол ACB называется углом, вписанным в окружность с центром в точке О. Точка С принадлежит окружности, то есть лежит на ней. Угол опирается на дугу АВ.

Чему равен центральный угол

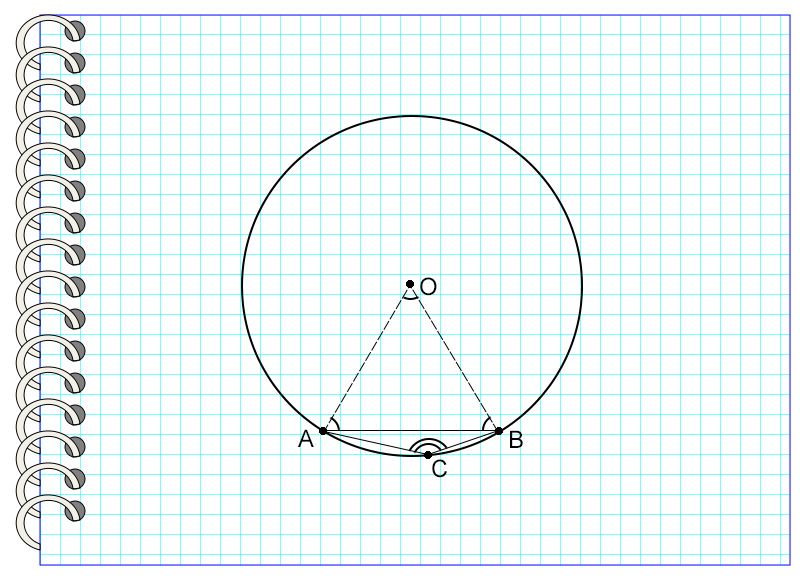
Для того чтобы успешно справляться с задачами по геометрии, недостаточно уметь различать вписанный и центральный углы. Как правило, для их решения нужно точно знать, как найти центральный угол в окружности, и уметь вычислить его значение в градусах.

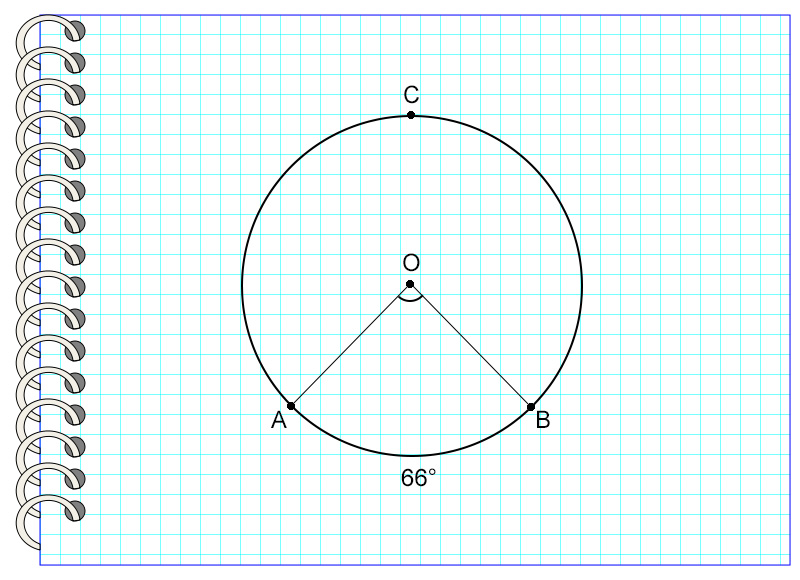
Итак, центральный угол равен градусной мере дуги, на которую он опирается.

На картинке угол АОВ опирается на дугу АВ, равную 66°. Значит, угол АОВ также равен 66°.

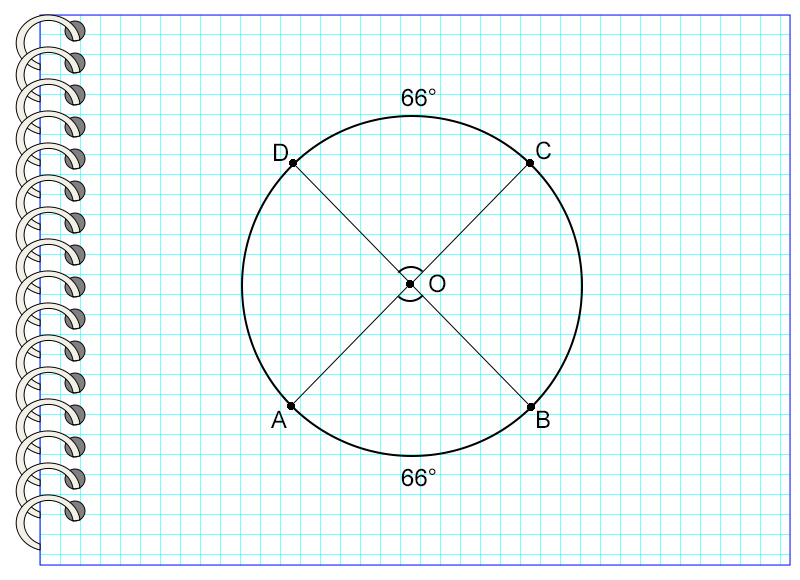
Таким образом, центральные углы, опирающиеся на равные дуги, равны.

На рисунке дуга DC равна дуге AB. Значит, угол АОВ равен углу DOC.

Как найти вписанный угол

Может показаться, что угол, вписанный в окружность, равен центральному углу, который опирается на ту же дугу. Однако это грубая ошибка. На самом деле, даже просто посмотрев на чертеж и сравнив эти углы между собой, можно увидеть, что их градусные меры будут иметь разные значения. Так чему же равен вписанный в окружность угол?

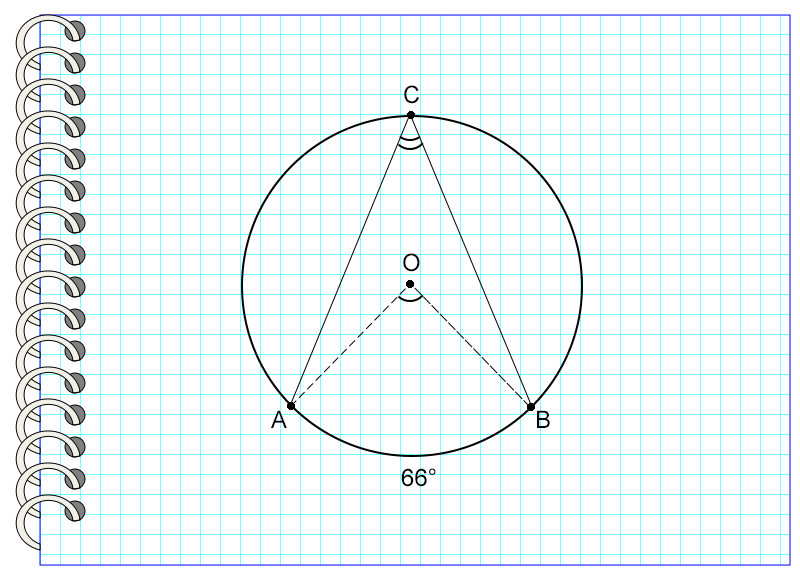
Градусная мера вписанного угла равна одной второй от дуги, на которую он опирается, или половине центрального угла, если они опираются на одну дугу.

Рассмотрим пример. Угол АСВ опирается на дугу, равную 66°.

Значит, угол АСВ = 66° : 2 = 33°

Рассмотрим некоторые следствия из этой теоремы.

• Вписанные углы, если они опираются на одну и ту же дугу, хорду или равные дуги, равны.
• Если вписанные углы опираются на одну хорду, но их вершины лежат по разные стороны от нее, сумма градусных мер таких углов составляет 180°, так как в этом случае оба угла опираются на дуги, градусная мера которых в сумме составляет 360° (вся окружность), 360° : 2 = 180°
• Если вписанный угол опирается на диаметр данной окружности, его градусная мера равна 90°, так как диаметр стягивает дугу равную 180°, 180° : 2 = 90°
• Если центральный и вписанный углы в окружности опираются на одну дугу или хорду, то вписанный угол равен половине центрального.

Где могут встретиться задачи на эту тему? Их виды и способы решения

Так как окружность и ее свойства – это один из важнейших разделов геометрии, планиметрии в частности, то вписанный и центральный углы в окружности – это тема, которая широко и подробно изучается в школьном курсе. Задачи, посвященные их свойствам, встречаются в основном государственном экзамене (ОГЭ) и едином государственном экзамене (ЕГЭ). Как правило, для решения этих задач следует найти углы на окружности в градусах.

Углы, опирающиеся на одну дугу

Этот тип задач является, пожалуй, одним из самых легких, так как для его решения нужно знать всего два простых свойства: если оба угла являются вписанными и опираются на одну хорду, они равны, если один из них – центральный, то соответствующий вписанный угол равен его половине. Однако при их решении нужно быть крайне внимательным: иногда бывает сложно заметить это свойство, и ученики при решении таких простейших задач заходят в тупик. Рассмотрим пример.

Дана окружность с центром в точке О. Угол АОВ равен 54°. Найти градусную меру угла АСВ.

Эта задача решается в одно действие. Единственное, что нужно для того, чтобы найти ответ на нее быстро – заметить, что дуга, на которую опираются оба угла – общая. Увидев это, можно применять уже знакомое свойство. Угол АСВ равен половине угла АОВ. Значит,

1) АОВ = 54° : 2 = 27°.

Углы, опирающиеся на разные дуги одной окружности

Иногда в условиях задачи напрямую не прописана величина дуги, на которую опирается искомый угол. Для того чтобы ее вычислить, нужно проанализировать величину данных углов и сопоставить их с известными свойствами окружности.

В окружности с центром в точке О угол АОС равен 120°, а угол АОВ – 30°. Найдите угол ВАС.

Для начала стоит сказать, что возможно решение этой задачи с помощью свойств равнобедренных треугольников, однако для этого потребуется выполнить большее количество математических действий. Поэтому здесь будет приведен разбор решения с помощью свойств центральных и вписанных углов в окружности.

Итак, угол АОС опирается на дугу АС и является центральным, значит, дуга АС равна углу АОС.

Точно так же угол АОВ опирается на дугу АВ.

Зная это и градусную меру всей окружности (360°), можно с легкостью найти величину дуги ВС.

ВС = 360° – АС – АВ

ВС = 360° – 120° – 30° = 210°

Вершина угла САВ, точка А, лежит на окружности. Значит, угол САВ является вписанным и равен половине дуги СВ.

Угол САВ = 210° : 2 = 110°

Задачи, основанные на соотношении дуг

Некоторые задачи вообще не содержат данных о величинах углов, поэтому их нужно искать, исходя только из известных теорем и свойств окружности.

Найдите угол, вписанный в окружность, который опирается на хорду, равную радиусу данной окружности.

Если мысленно провести линии, соединяющие концы отрезка с центром окружности, то получится треугольник. Рассмотрев его, можно заметить, что эти линии являются радиусами окружности, а значит, все стороны треугольника равны. Известно, что все углы равностороннего треугольника равны 60°. Значит, дуга АВ, содержащая вершину треугольника, равна 60°. Отсюда найдем дугу АВ, на которую опирается искомый угол.

АВ = 360° – 60° = 300°

Угол АВС = 300° : 2 = 150°

В окружности с центром в точке О дуги соотносятся как 3:7. Найдите меньший вписанный угол.

Для решения обозначим одну часть за Х, тогда одна дуга равна 3Х, а вторая соответственно 7Х. Зная, что градусная мера окружности равна 360°, составим уравнение.

По условию, нужно найти меньший угол. Очевидно, что если величина угла прямо пропорциональна дуге, на которую он опирается, то искомый (меньший) угол соответствует дуге, равной 3Х.

Значит, меньший угол равен (36° * 3) : 2 = 108° : 2 = 54°

В окружности с центром в точке О угол АОВ равен 60°, а длина меньшей дуги – 50. Вычислите длину большей дуги.

Для того чтобы вычислить длину большей дуги, нужно составить пропорцию – как меньшая дуга относится к большей. Для этого вычислим величину обеих дуг в градусах. Меньшая дуга равна углу, который на нее опирается. Ее градусная мера составит 60°. Большая дуга равна разности градусной меры окружности (она равна 360° вне зависимости от остальных данных) и меньшей дуги.

Большая дуга равна 360° – 60° = 300°.

Так как 300° : 60° = 5, то большая дуга в 5 раз больше меньшей.

Большая дуга = 50 * 5 = 250

Итак, конечно, существуют и другие подходы к решению подобных задач, но все они так или иначе основаны на свойствах центральных и вписанных углов, треугольников и окружности. Для того чтобы успешно их решать, необходимо внимательно изучать чертеж и сопоставлять его с данными задачи, а также уметь применять свои теоретические знания на практике.

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

• Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

• Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

• Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

• Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

• Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

• Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

• Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

[spoiler title=”источники:”]

http://fb.ru/article/445770/uglyi-v-okrujnosti-tsentralnyiy-i-vpisannyiy-svoystva-i-sposobyi-nahojdeniya

http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly

[/spoiler]

Как узнать угол треугольника

В задачах по геометрии для разных классов целью или промежуточным действием является нахождение угла треугольника. Разберем, как это делается в разных видах треугольников.

1

Универсальные формулы, чтобы узнать угол треугольника

Формулы, приведенные ниже, подойдут для любого типа треугольников.

• ∠А = 180°-(∠В+∠С) (т.к. сумма всех углов треугольника равна 180°).
• ∠А = 180°-∠OAB (т.к. ∠OAB внешний).

2

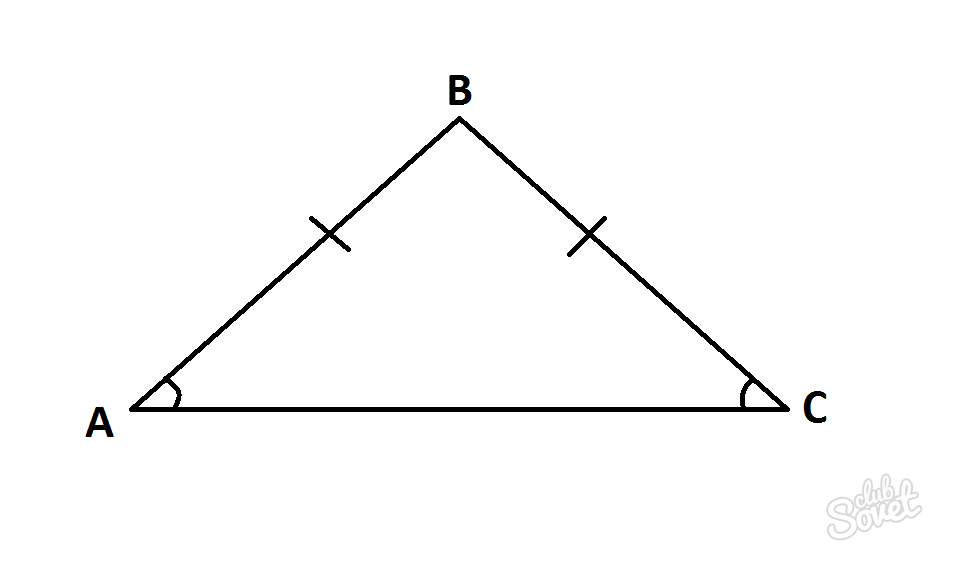
Узнать угол в равнобедренном треугольнике

Равнобедренный треугольник можно опознать по двум равным боковым сторонам или по двум равным углам.

• ∠B = 180°-2•∠A.
• ∠А =∠С (т.к. углы при основании равнобедренного треугольника равны).
• Если ∠А=60°, то все углы равны 60°, а треугольник ABC – равносторонний.

3

Узнать угол в прямоугольном треугольнике

Углы в прямоугольном треугольнике можно найти либо одним из способов, представленных в пункте 1, либо при помощи тригонометрических функций – синуса, косинуса, тангенса и котангенса.

Тригонометрические функции

Если вам даны две стороны, найти угол можно по следующему алгоритму:

• Смотрим, какими являются данные стороны по отношению к прямому углу (катет, гипотенуза) и углу, который нужно найти (прилежащий/противолежащий катет).
• Находим тригонометрическую функцию, которая подходит нам.
• Находим, чему она равна, подставив значения данных сторон.
• Вычисляем угол при помощи обратной функции (арксинус, арккосинус и т.д.).

Теоремы синуса и косинуса

Сами теоремы вы видите на картинке ниже. С помощью них можно узнать косинус или синус интересующего вас угла, и через него вычислить значение.