В прошлой части мы обсудили, как может изменяться момент стержня и как выяснить, не разрушится ли он под действием нормальных и касательных сил. Однако под воздействием момента стержни могут изгибаться и изменять форму, что может приводить к неправильной работе конструкций или даже их разрушению в процессе эксплуатации. Сегодняшняя статья посвящена вопросу нахождения прогибов и углов наклона при изгибе.
Уравнение кривой
В прошлой части мы выяснили, что для нахождения момента нам необходимо знать какой у дуги изгиба радиус кривизны, какой у сечения статический момент и какой модуль Юнга у материала балки:
Затем мы устранили из уравнения такое значение как радиус кривизны, из наших уравнений, так как нас не столько волновало, как под воздействием изменится балка, сколько не сломается ли она.
Однако сейчас нас интересует именно то, как будет деталь изгибаться под воздействием моментов, как будет меняться геометрия .
В прошлый раз мы не заостряли внимание на вопросе «что такое радиус кривизны», да и просто «что такое кривизна». В этой части мы данную проблему решим, а также объясним как это значение поможет нам в сопромате вычислить деформации изгиба.
Фактически, до этого момента мы оперировали не столько радиусом, сколько кривизной, которая обратно пропорциональна радиусу:
А сейчас мы поговорим о том, какое значение она имеет с точки зрения геометрии.
Если нет желания смотреть, как с точки зрения математики выводятся геометрические характеристики, можно промотать до следующего жирного шрифта и принять за данность выводы.
Кривизна – это то, насколько сильно изменяется угол наклона касательной к нашей кривой за единицу длины дуги.
Так как любую кривую можно представить как сумму бесконечно малых дуг, принадлежащих разным окружностям, стоит посмотреть, на сколько будет изменяться угол в двух точках ее дуги.
Углы будем измерять в радианах (180°=π, 360°=2π). Длина окружности равна удвоенному произведению радиуса на π: l=2πR. Круг — фигура симметричная, и поэтому в любой точке кривизна будет одинакова и равна:
χ=frac{2π}{2π*R}=frac{1}{R}
Вот так и находилась формула кривизны балки. И теперь мы хотим поставить её на службу поиска формы балки.
Нам нужно найти изменение угла за бесконечно малый пройденный путь, и мы имеем некоторую функцию. При этом её первая производная будет равна тангенсу угла с осью x, которую мы обозначим греческой тета θ:
Нам же для вычисления кривизны необходимо найти изменение угла θ:
Гуглим таблицу дифференциалов, находим, что дифференциал от тангенса равен следующему выражению:
d(arctg (x))=frac{dx}{1+x^2}
Так как функция сложная (y’ — тоже какая-то функция, пусть нам и не известная), получившееся значение надо будет домножить на производную от аргумента:
dθ=frac{dx}{(1+(y’)²)}*y’’
Кривизна же — это изменение угла за пренебрежительно малый отрезок длины:
Уравнение угла наклона нам известно. Теперь нам нужно вычислить длину малой дуги. Достаточно малой, чтобы можно было пренебречь кривизной и считать её прямой. Тогда мы сможем воспользоваться теоремой Пифагора:
Где dx – пройденный путь по оси x, а dy – по оси y.
Нам для красоты уравнения хотелось бы избавиться побыстрее от дифференциалов, чтобы в формуле остались только производные. Для этого мы делим все, что было под корнем на (dx)^2:
frac{(dx)^2}{(dx)^2}+frac{(dy)^2}{(dx)^2}=1+(y')^2
Так как (dx)^2/(dx)^2=1, а (dy)/(dx) – это производная y по x.
Чтобы уравновесить данное вмешательство, мы должны домножить все выражение на dx (т.к. √(dx)^2=dx):
Теперь у нас есть все для нахождения кривизны:
χ=frac{dθ}{dl}=frac{dx}{(1+(y’)^2)}*y’’*frac{1}{dxsqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^2}
*frac{1}{sqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^{{3}}}
Отсюда стоит читать всем, даже тем, кому математика вывода кривизны не очень интересна.
Итак, мы смогли вычислить чему равна функция кривизны:
χ=frac{1}{R}=frac{y’’}{(sqrt{1+(y’)^2})^{3}}
Где y – прогиб (т.е. расстояние на которое выше или ниже окажется определенная точка балки, по сравнению с недоформированным состоянием), y’ – первая производная от неё, а y» – вторая (или кривизна).
Перед нами же стоит задача вычислить форму. Так как в сопротивлении материалов прогибы достаточно небольшие, изменением длины можно пренебречь. Следовательно, нам остается лишь вычислить изменение координаты y в зависимости от x. И в полученной формуле нам мешает это сделать очень объемный знаменатель (√(1+(y’)²)³.
Если подумать логически, то так как прогибы в сопромате достаточно небольшие, можно было бы не учитывать производную y’, так как она является отношением катетов треугольника, который бы получился опусти мы к оси x перпендикуляр.
Дело в том, что даже если прогиб (координата y) будет составлять 1/10 от x, производная в самом крайнем углу будет чуть больше 0,2x. А ее квадрат 0,04x. А (√(1+(y’)²)³ около 1,06.
Это не назвать пренебрежительно малым значением, однако его проще компенсировать коэффициентами запаса прочности. Да и прогиб этот слишком большой для основ сопротивления материалов (большими деформациями занимается отдельная дисциплина). Вот демонстрация прогиба в натуральном соотношении:
В результате, если мы проигнорируем знаменатель, получим формулу, которую уже можно будет использовать в дальнейших расчетах:
χ=θ’=y’’
Угол поворота и прогиб
Мы уже выяснили, что кривизна балки в каждой части зависит от момента, возникающего в этом сечении, статического момента и модуля Юнга материала, из которого это балка сделана:
Сегодня же мы будем решать обратную задачу и находить изгиб балки. В первой части статьи мы выяснили, что для малых изгибов радиус кривизны (он равен единице деленной на радиус кривизны) практически равен второй производной от прогиба (насколько по оси z поднимется или опустится балка в конкретной точке). В итоге мы, зная как распределяется момент, сможем посчитать вторую производную прогиба для каждой точки балки:
y’’=χ=frac{1}{R}=frac{M_z}{I_z×E}
Нам же интересна форма балки: углы её наклона и на сколько сантиметров выше или ниже она окажется.
Начнём с наклона. Как мы уже выяснили, первая производная будет равна тангенсу наклона. Тангенс равен отношению противолежащего катета к прилежащему:
Углы наклона у нас будут маленькими, поэтому прилежащий катет будет практически равен радиусу. Отношение противолежащей стороны к радиусу является синусом:
А синус малого угла, как мы уже выяснили вначале статьи, численно равен углу в радианах.
Примечание: мы выяснили, что для малых углов тангенс, синус и угол численно равны. Эта закономерность важна не только в сопромате, но и в большинстве других инженерных наук. Например, в геодезии, при определении величины малых скатов.
Как следствие, для того, чтобы найти угол наклона, нам необходимо проинтегрировать кривизну:
θ=∫y''dx=∫frac{M_z*dx}{J_z*E}=frac{1}{J_z*E}∫M_z*dx=y'+C
Углы и прогибы балки под воздействием момента
В простейшем случае к балке приложен только момент:
В таком случае значение момента является константой. Обозначим ее как M. Тогда найти прогиб можно по формуле:
θ=∫y''dx=frac{1}{I_z*E}∫M_z*dx=frac{M_z*x}{I_z*E}+C
Остается найти константу интегрирования. Так как в начале координат балка жестко закреплена, угол в месте закрепления будет равен нулю, как следствие, константа тоже будет равна нулю. Эпюра угла наклона будет выглядеть вот так:
Для того, чтобы найти прогибы надо, соответственно, проинтегрировать получившееся выражение еще раз:
y=∫θdx=∫frac{M_z*x*dx}{I_z*E}+∫Cdx=frac{M_z*x^2*dx}{2*I_z*E}+Cx+D
Константу C мы уже знаем, а константу D можно найти по той же логике: балка жестко закреплена в начальной точке, а значит прогиб y в ней будет равен 0. А полученная нами формула приводит к нулю в начале координат только при нулевой константе:
(M*0)2/2+C*0+D=0, только если D=0
Ну а эпюра прогибов будет выглядеть следующим образом:
Углы и прогибы балки под воздействием силы
В случае же, если момент появляется под воздействием силы, эпюры как бы сдвигаются на одну вперед:
Линейной станет функция момента, а угол будет постепенно увеличиваться (вначале быстро, потом медленнее, так как момент будет меньше).
Mz=P(l-x), где Mz— момент возникающий в балке в точке, которая расположена на расстоянии x от места закрепления балки, а l – длина балки.
Получили мы это уравнение следующим образом: мы знаем что в месте закрепления возникает момент который компенсирует момент от воздействия силы на конце балки:
Также в месте закрепления будет возникать сила, которая будет компенсировать силу внешнюю:
Когда мы будет отдаляться от точки закрепления на величину x, сила реакции опоры будет создавать для нашего сечения момент MRa=Ra*x. Он будет складываться с моментом передавшимся с начала балки:
M_z=M_{z_{0}}-M_{R_{a}}=\=p*l+R_a*x=P*l-P*x=\=P(l-x)
Зная функцию распределения момента мы можем найти функции наклона и прогиба.
Наклон будет увеличиваться по параболе:
θ=∫frac{(P*(l-x))*dx}{I_z*E}=frac{P*(l-x)^2}{2*I_z*E}+C
Ну а прогиб будет изменяться уже по кубическому закону:
y=∫frac{P*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{P*(l-x)^3*dx}{6*I_z*E}+C*x+D
Примечание: если проще, то l-x потому, что в нулевой координате момент равен расстоянию до силы, а затем уменьшается на то расстояние, которое мы до нее прошли
Углы и прогибы балки под воздействием равномерно-распределенной нагрузки
В случае с равномерно-распределенной нагрузкой ситуация абсолютно аналогична: эпюры «сдвигаются» на одну относительно воздействия силы. Поперечная сила изменяется по линейному закону Qy=Ra-qx=ql-qx=q(l-x), момент по параболе Mz=q(l-x)2/2:
Угол наклона, соответственно, будет определяться кубической функцией:
θ=∫frac{q*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{q*(l-x)^3*dx}{6*I_z*E}+C
А прогиб уже функцией четвёртой степени:
y=∫frac{q*(l-x)^3*dx}{6*I_z*E}=\=frac{q*(l-x)^4*dx}{24*I_z*E}+Cx+D
Расчет балки на прогибы и углы наклона. Метод начальных параметров. Пример
На практике достаточно редко случается ситуация, при которой на конструкцию действует только одна сила, а сама конструкция состоит из одной балки, закрепленной только в одном месте. Разберем как пример расчёт балки, в которой есть все виды воздействий:
Примечание: среди внешних воздействий отсутствует сила. Мы сделали это для того, чтобы не загружать статью лишними расчётами: сила реакции опоры в расчетах ничем не отличается от силы внешней.
Первым делом, нужно заменить места закрепления на силы, которые они создают для поддержания равновесия балки. В данном случае это две вертикальные силы (моментов шарнирные опоры не создают):
Теперь наша задача найти эти силы. Сделать это довольно просто: составляем уравнение сил по оси y и момента для точки закрепления балки.
Уравнение равновесия сил по оси Y:
R_a-ql+R_b=R_a-30+R_b=0, R_a+R_b=30
Уравнение равновесия момента в левой точке закрепления:
M_a=ql*a+frac{15l^2}{2}+M-d*R_b=30+30-10-5R_b=0
Где a — расстояние до начала действия равномерно-распределенной нагрузки, d — расстояние до опоры b.
Из уравнения момента мы можем найти, чему равна сила реакции правой опоры:
Подставляем это значение в уравнение равновесия сил и получаем силу реакции первой опоры:
R_a+R_b=R_a+14=30, R_a=16
Для того, чтобы найти прогибы, нам надо составить уравнения момента для каждого участка. В нашем случае удобнее всего Теперь найдём функцию распределения момента для первого участия. Так как в точке a балка закреплена не жестко, момент в ней по условию равен нулю. В ней возникает только сила реакции опоры Ra=16.
Момент на первом участке будет зависеть от удаления от этой силы:
Для нахождения угла наклона это выражение надо проинтегрировать:
θ_{(I)}=frac{1}{I_zE}∫R_axdx=frac{R_ax^2}{2I_zE}+C
И ещё раз для получения прогиба:
y_{(I)}=frac{1}{I_zE}∫frac{R_ax^2dx}{2}+∫Cdx=frac{R_ax^3}{6I_zE}+Cx+D
Затем нам нужно найти геометрию балки на участке с равномерно-распределенной нагрузкой.
При этом, момент на этом участке будет зависеть от двух составляющих: от силы реакции Ra с первого участка и от нагрузки q.
M_{z_{(II)}}=f(R_a,x)+f(q,x)
Функция момента (Mz(I)=Ra*x=12x) возникающего от силы на первом участке будет справедлива и для нашего участка: момент по-прежнему будет равен произведению плеча на силу.
По мере того, как мы будем отступать от начала действия равномерно-распределенной нагрузки, момент будет увеличиваться по квадратичному закону (почему, можно прочитать в статье посвященной теореме Журавского) M(q)=qx’^2/2, где x’ — расстояние от начала приложения нагрузки.
Нам удобнее все расчёты проводить из одной точки, поэтому для второго участка x’=x-a, где a координата начала приложения нагрузки. Таким образом, уравнение момента на втором участке будет выглядеть так:
Mz_{(II)}=Ra*x-frac{q(x-a)^2}2=16x-frac{15(x-1)^2}2
Интегрируем чтобы найти наклон:
θ_{(II)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6)+C
И ещё раз, чтобы найти прогиб:
y_{(II)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32})
На следующем участке действие равномерно-распределенной нагрузки заканчивается. При этом, мы хотим чтобы q(x-a)2/2 в формуле осталась: всё-таки она вносит вклад в момент и геометрию стержня.
Чтобы эту небольшую проблему исправить, мысленно продолжим распределенную силу до конца конструкции, но приложим в противовес ей точно такую же, направленную в другую сторону:
Таким образом на следующий участок стержня (который начинается в точке b) дополнительно будет приложена распределенная нагрузка q, которая будет создавать момент M=q(b-x)2/2.
Суммарный момент для третьего участка будет равен:
Mz_{(III)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2
Ну и, соответственно, найти наклон и прогибы не составляет трудности:
θ_{(III)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6)+C
y_{(III)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32})+Cx+D
Четвёртый участок начинается в месте приложения момента и заканчивается на второй опоре.
Составляем уравнение момента:
Mz_{(IV)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2+10
Где c — расстояние от начала координат до места приложения момента, а x-c, расстояние между точкой, которую мы рассматриваем и местом приложения момента. В нулевой степени это выражение всегда равно единице, поэтому для уравнения момента это константа. Но после интегрирования это выражение становится важной частью уравнения наклона:
θ_{(IV)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))+C
А затем и уравнения прогиба:
y_{(IV)}=\frac{1}{Iz*E}∫(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32}+frac{M(x-c)^2}{2})+Cx+D
Остается вычислить константы интегрирования. На первой и последней опоре прогибы (т.е. вертикальные перемещения) будут равны нулю. Подставляем x=0 в уравнение первого отрезка:
y_{(I)}=frac{R_a0^3}{6I_zE}+C*0+D
И выясняем, что константа интегрирования D равна нулю.
Подставляя константу интегрирования D в уравнение последнего участка для закрепленного конца балки (т.е. x=l=5) мы получим следующее уравнение:
0=frac{1}{Iz*E}*(frac{16*5^3}6-frac{15(5-1)^4}{32}+frac{15(5-3)^4}{32}+frac{10(5-4)^2}{2})+С*5+0
Выражение равно нулю по причине того, что прогибы в месте закрепления образовываться никак не могут.
Решив уравнение мы получим значение второй константы интегрирования:
С=frac{225,83}{5*Iz*E}=frac{45,17}{Iz*E}
Дальше остается лишь подставить эти константы в уравнения и мы получим уравнения наклонов и прогибов.
Итак, мы выяснили по каким законам будет прогибаться каждый участок балки.
Если резюмировать, то для получения уклона и прогиба на некотором участке, нам нужно просуммировать все воздействия и их проинтегрировать.
Метод начальных параметров
В общем виде углы наклона будут считаться так:
А прогибы так:
Примечание: не забывайте компенсировать равномерно-распределенную нагрузку в точке, где она заканчиваться!
На практике гораздо целесообразнее считать момент, наклон и прогиб сразу для всей балки, с помощью трех систем уравнений: системы моментов, наклонов и прогибов.
Уравнения моментов для каждого участка
Так их удобнее составлять, так как достаточно просто для каждого нового участка добавлять воздействия:
Уравнения наклонов
Как можно заметить, для того, чтобы из системы уравнений моментов получить систему уравнений наклонов достаточно проинтегрировать каждый член и добавить константу интегрирования C:
Уравнения прогибов
Как ни странно, для того, чтобы их получить, достаточно проинтегрировать каждый из членов уравнения наклона, добавить ещё одну константу интегрирования D, а первую константу C умножить на x.
Итак, подошёл к концу разговор о том, как материалы противодействуют изгибам. В прошлых частях мы уже выяснили, какие нормальные напряжения возникают в материале при попытке его согнуть. Обсудили и как с распределением момента связаны поперечные силы и касательные напряжения. А сейчас выяснили и как будет материал менять свою форму под воздействием изгиба.
Это имеет далекоидущие последствия для всех инженерных дисциплин и опирающихся на них специальностей. Например, ротор турбин, являющийся по своей сути длинным стержнем на опорах, под силой тяжести достаточно сильно изгибается. По этой причине для всех турбин большой мощности противопоказан быстрый старт. Перед тем, как соединять статор и ротор, стержень турбины необходимо повращать, чтобы он избавился от изгибающих деформаций. Иначе лопатки будут цепляться и в лучшем случае деформироваться, а в худшем ломаться. Но это уже совсем другая история.
В следующей части мы поговорим о другом виде воздействия момента на стержень: о кручении.
Автор: К.А.Овчинников
Редактор: Сабуров Даниил
Эксперт: Ершов Марк
За консультативную поддержку по математической части огромная благодарность Гришиной Ольге Андреевне, старшему преподавателю кафедры высшей математики БГТУ ВОЕНМЕХ.
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники:
- Горбатовский Александр Александрович Дифференциальное уравнение изогнутой оси балки // Курс лекций по сопротивлению материалов МГТУ ИМ. Н.Э.БАУМАНА
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова
- http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi
- https://spravochnick.ru/matematika/krivizna_krivoy/krivizna_i_ee_vychislenie/
- iSopromat Метод начальных параметров. Расчет перемещений сечений балки // https://youtu.be/xRp-ViFUl7Y
4 140
Подборка формул для расчета балок и рам на изгиб и решения задач сопротивления материалов по расчету внутренних сил, напряжений, деформаций и перемещений при изгибе.
Обозначения:
σ — нормальные напряжения,
τ — касательные напряжения,
Qy – внутренняя поперечная сила,
Mx – внутренний изгибающий момент,
Ix – осевой момент инерции сечения балки,
Wx – осевой момент сопротивления сечения,
A — площадь поперечного сечения,
[σ], [τ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.
Расчет внутренних поперечных сил и изгибающих моментов
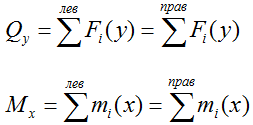
Формула кривизны балки в заданном сечении
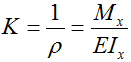
Расчет нормальных напряжений в произвольной точке сечения балки при изгибе
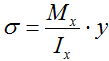
Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)
Осевые моменты инерции I и сопротивления W
Касательные напряжения в произвольной точке сечения при изгибе определяются по формуле Журавского:
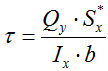
Здесь:
Sx* — статический момент относительно оси x отсеченной части сечения
b — ширина сечения на уровне рассматриваемой точки
Другие видео
Условие прочности балки по касательным напряжениям
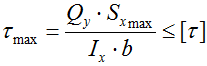
Дифференциальное уравнение линии изогнутой оси балки
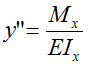
Уравнения метода начальных параметров (МНП)
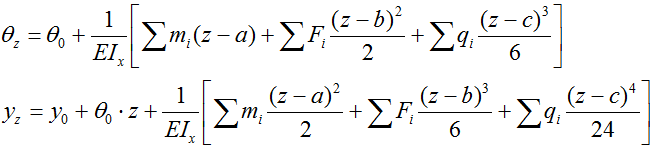
θz, yz — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ0, y0 — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,
a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.
Пример расчета перемещений в балке методом начальных параметров >
Другие формулы >
Примеры решения задач >
Краткая теория >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).
Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:
То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:
А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:
Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема
Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;
• ПРОТИВ часовой стрелки — учитываем её с «минусом».
Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.
Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.
В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;
• нижние волокна, то нужно учесть его с «плюсом».
Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:
Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:
Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.
Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:
Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:
Откладываем полученные значения:
Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.
Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:
Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:
Показываем окончательную эпюру изгибащих моментов:
Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:
Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:
Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:
Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:
Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:
Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:
Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:
Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:
Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:
Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:
Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:
Уравнение для изгибающих моментов будет следующее:
Тогда значения на эпюре будут такими:
На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:
Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:
Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:
Определим реакции опор:
Рассчитываем первый участок:
Строим эпюры на первом участке:
Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:
Затем подставить это значение в уравнение для изгибающих моментов:
Теперь можем указать экстремум на эпюре:
Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:
Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
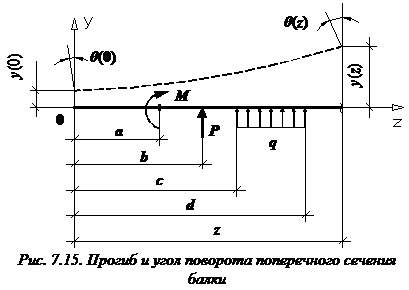
Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений
Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
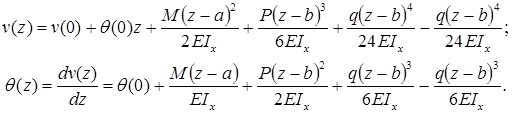
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб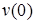 
и угол поворота 
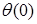балки в начале координат (начальные параметры) определяются из условий закрепления балки.
Уравнение упругой линии балки на примере
Определим прогиб балки на консоли при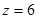 
м, то есть 
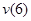. Запишем универсальное уравнение упругой линии балки:
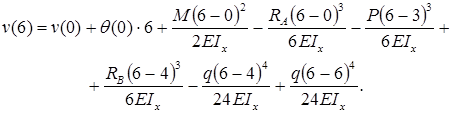
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: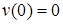 
.
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
,
.
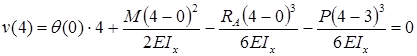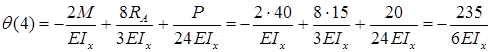Прогиб консоли при z=6м:
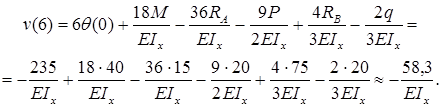
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
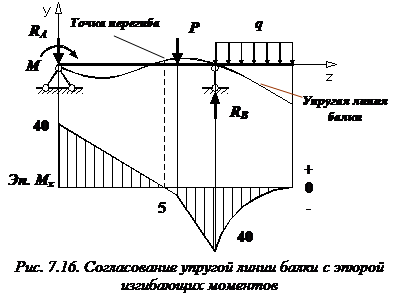
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
6.1. Понятие об упругой
линии. Прогиб и угол поворота.
Дифференциальное уравнение упругой
линии. Условие жесткости при изгибе
Чтобы судить о работе изгибаемых балок,
недостаточно знать только напряжения,
которые возникают в сечениях балки от
заданной нагрузки. Вычисленные напряжения
позволяют проверить прочность системы.
Однако весьма прочные балки могут
оказаться непригодными к эксплуатации
из-за недостаточной жесткости. Если
балка при нагружении сильно прогибается,
то при эксплуатации сооружения, имеющего
гибкие балки, появятся затруднения и,
кроме того, могут возникнуть колебания
балки с большими амплитудами, а вместе
с тем и значительные дополнительные
напряжения.
Под жесткостью
следует понимать способность
элеменов конструкций и деталей машин
сопротивляться внешним нагрузкам без
видимых деформаций.
Расчет на жесткость заключается в оценке
упругой податливости балки под действием
приложенных нагрузок и подбор таких
размеров поперечного сечения, при
которых перемещения не будут превышать
установленных нормами пределов. Для
выполнения такого расчета необходимо
научиться вычислять перемещения сечений
балки под действием любой внешней
нагрузки.
Рассмотрим деформацию
балки при простом изгибе. Ось балки
(Рис.6.1,а) под действием нагрузки,
расположенной в одной из главных
плоскостей инерции (в плоскости
),
искривляется в той же плоскости, а
поперечные сечения поворачиваются и
одновременно получают поступательные
перемещения. Искривленная ось балки
называетсяизогнутой
осью или упругой
линией. На рис.
6.1 упругая линия изображена тонкой
кривой.
Точка
,
лежащая на оси в сечении, отстоящем не
расстоянии
от начала координат, переместится в
точку
.
Обозначим перемещение произвольной
точки оси бруса в направлении оси
через
,
а перемещение вдоль оси бруса – через
.
Если в точке
провести касательную к оси изогнутой
балки, то по отношению к первоначальному
положению оси она будет повернута на
угол
.
Одновременно на тот же угол повернется
сечение в точке
.
Таким образом, три величины
,
и
являются компонентами перемещения
произвольного поперечного сечения
балки. Перемещение
центра тяжести сечения по направлению,
перпендикулярному к оси балки, называетсяпрогибом.
Наибольший прогиб называется стрелой
прогиба и
обозначается буквой
.
Угол
,
на который каждое сечение поворачивается
по отношению к своему первоначальному
положению, называется углом поворота
сечения. Как уже отмечалось, угол поворота
также может быть определен как угол
между касательной к упругой линии и
осью
.
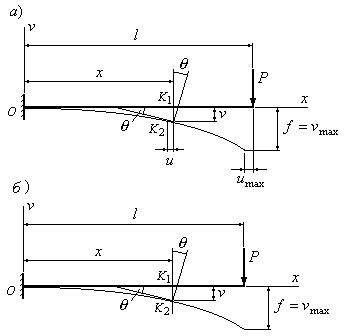
Рис.6.1
Проверка жесткости
балок сводится к требованию, в соответствии
с которым наибольший прогиб
не должен превышать определенной доли
пролета:
.
Число
устанавливается нормами проектирования
примерно в пределах от 300 до 1000. Для
ответственных сооружений, например,
для железнодорожных мостов, величина
принимается равной 1000.
Отсюда видно, что
прогибы при изгибе, как правило, малы
по сравнению с пролетом балки. Это
позволяет внести некоторые упрощения.
Во-первых, при малых прогибах
угол наклона касательной к оси изогнутой
балки можно определять с помощью
выражения:
.
(6.1)
Во-вторых, горизонтальными
перемещениями
можно пренебречь, так как они существенно
меньше
(
).
В связи с этим при расчетах будем
пользоваться условной схемой перемещений,
изображенной на рис 6.1,б. Согласно этой
схеме каждая точка перемещается
перпендикулярно продольной оси бруса.
Для определения полной картины деформаций
необходимо получить уравнение упругой
линии
.
Исходя из физической природы изогнутой
оси бруса, можем утверждать, что упругая
линия должна быть непрерывной и гладкой
кривой, следовательно, на протяжении
всей оси бруса должны быть непрерывны
функция и ее первая производная. Прогибы
и углы поворота и являются перемещениями
сечений балок при изгибе. Деформация
того или иного участка балки определяется
его кривизной.
При выводе формулы для нормальных
напряжений при изгибе нами была получена
связь между кривизной и изгибающим
моментом:
.
(6.2)
Из курса высшей математики известно
следующее уравнение кривизны плоской
кривой:
.
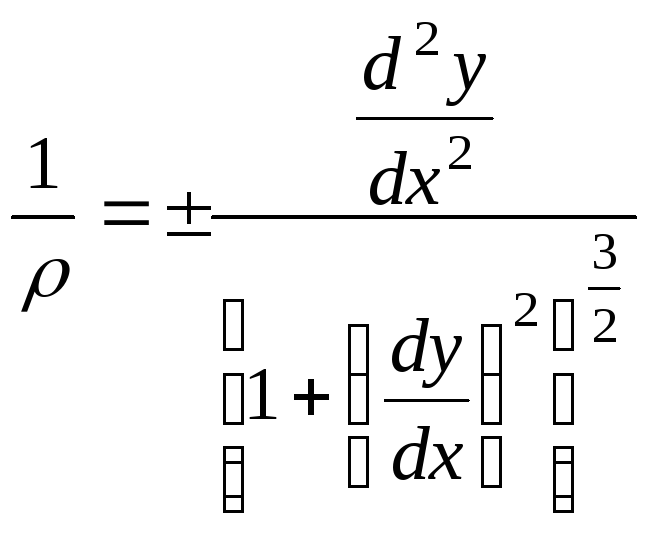(6.3)
Подставляя значение
кривизны в равенство (6.2) и заменяя
координату
прогибом
,
получим точное дифференциальное
уравнение упругой линии балки:
.
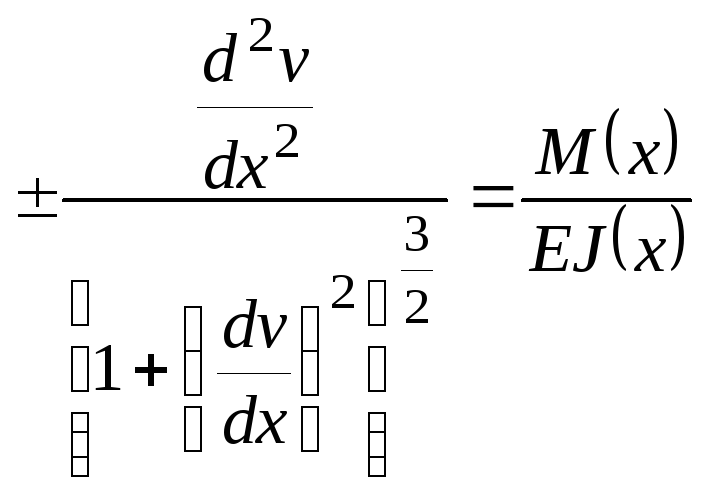(6.4)
Интегрирование этого
нелинейного дифференциального уравнения
связано с большими трудностями. Учитывая,
что на практике приходится иметь дело
с малыми прогибами и что тангенсы углов
наклона
касательной к оси будут малы, квадратом
первой производной
по
сравнению с единицей можно пренебречь.
Тогда получим приближенное (основное)
дифференциальное уравнение
(6.5)
Два
знака в уравнении (6.5) поставлены потому,
что знак кривизны
может не совпадать со знаком изгибающего
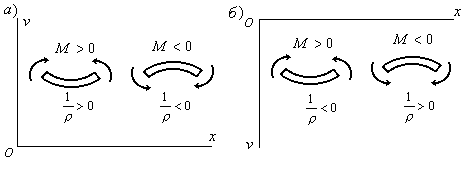
момента. Знак кривизны зависит от
направления осей координат. Знак
изгибающего момента был выбран в
зависимости от того, где расположены
растянутые волокна. Так, например, для
случая, когда ось
направлена вверх, положительному моменту
(Рис.6.2,а) соответствует положительная
кривизна, а отрицательному – отрицательная
кривизна.
Рис
6.2
Таким
образом, в случае, когда ось
направлена вверх, знаки кривизны и
изгибающего момента совпадают. Поэтому
в дифференциальном уравнении берется
знак“+”.
Если ось
направлена вниз, то знаки у кривизны и
изгибающего момента будут различны
(Рис.6.2,б). Поэтому в этом случае в правой
части уравнения (6.5) берется знак“”.
6.2. Метод непосредственного
интегрирования приближенного (основного)
дифференциального уравнения упругой
линии
Решая
задачу аналитическим методом, углы
поворота
и прогибы
вычисляют последовательным интегрированием
приближенного дифференциального
уравнения (6.5). Проинтегрировав уравнение
(6.5) первый раз, получим выражение для
угла поворота
:
,
(6.6)
где
постоянная интегрирования.
Интегрируя
второй раз, получим выражение для прогиба
:
,
(6.7)
где
и
постоянные интегрирования.
Для
вычисления интегралов, входящих в (6.6)
и (6.7), необходимо сначала написать
аналитические выражения для изгибающего
момента и жесткости. Постоянные
интегрирования находятся
из граничных условий,
которые зависят от условий перемещения
границ участков балки.
Рассмотрим несколько
примеров применения метода непосредственного
интегрирования приближенного уравнения
упругой линии балки.
Пример
6.1. Определить
стрелу прогиба и угол поворота сечения
В балки, изображенной на рис.6.3.
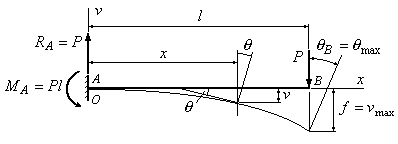
Рис.6.3
Решение:
1. Из условий
равновесия определяем опорные реакции:
;
.
2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Ось
направляем вверх, ось
вправо.
3.
Составляем уравнение изгибающего
момента в сечении
:
.
4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Интегрируем
уравнение первый раз. Получаем:
.
(а)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:
.
(б)
Так как в заделке прогиб и угол поворота
равны нулю, то для определения постоянных
интегрирования граничные условия имеют
вид:
при
;
при
.
Из
уравнения (а) видно, что постоянная
представляет собой угол поворота в
начале координат (сечении А). Задавая в
уравнении (а)
,
находим
.
Из уравнения (б) следует, что постоянная
прогиб в начале координат. Задавая в
уравнении (б)
,
получаем
.
Таким образом,
получаем следующие выражения для прогиба
и угла поворота:
,
.
Подставляя
в первое уравнение
,
найдем стрелу прогиба:
.
Подставляя
во второе уравнение
,
найдем максимальный угол поворота
.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота показывает,
что сечение В повернулось не против, а
по часовой стрелке.
Пример
6.2. Определить
стрелу прогиба двухопорной балки и углы
поворота опорных сечений А и В (рис.6.4).
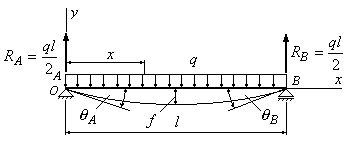
Рис.6.4
Решение:
1. Из условий
равновесия определяем опорные реакции:
.
2.
Выбираем начало координат
на левом конце балки, совмещая его с
точкой А. Ось
направляем вверх, ось
вправо.
3.
Составляем уравнение изгибающего
момента в сечении
:
.
4. Предполагая, что
жесткость балки постоянна, записываем
приближенное дифференциальное уравнение
упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Интегрируем
уравнение первый раз. Получим:
.
(в)
Интегрируя
еще раз, получаем уравнение для прогиба
в сечении
:
.
(г)
Постоянные
интегрирования найдем из граничных
условий:
при
;
при
.
Подставляя
в уравнение (г)
и приравнивая прогиб нулю, получим
;
подставляя в это же уравнение
,
находим постоянную интегрирования
:
.
Найденные значения
постоянных интегрирования подставим
в уравнения (в) и (г) и получим уравнения
углов поворота и прогибов:
;
.
Подставляя
и
в первое уравнение, получим углы поворота
соответственно сечений А и В:
;
.
В
силу симметрии нагрузки максимальный
прогиб
будет посредине балки. Подставляя во
второе уравнение
,
получим:
.
Как
и в предыдущем примере, знак “”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Знак“”
в выражении угла поворота
показывает, что сечение А повернулось
не против, а по часовой стрелке, знак“+”
в выражении угла поворота
показывает, что сечение В повернулось
против часовой стрелки.
Пример
6.3. В сколько
раз прогиб в сечении В на конце изображенной
на рис.6.5 балки, больше, чем прогиб в
сечении С
посредине
балки?
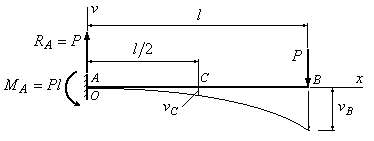
Рис.6.5
Решение:
Воспользуемся
результатами, полученными в примере
6.1. Запишем окончательное выражение для
прогиба:
и подставим в это
уравнение координаты точек С и В. Получим:
при
;
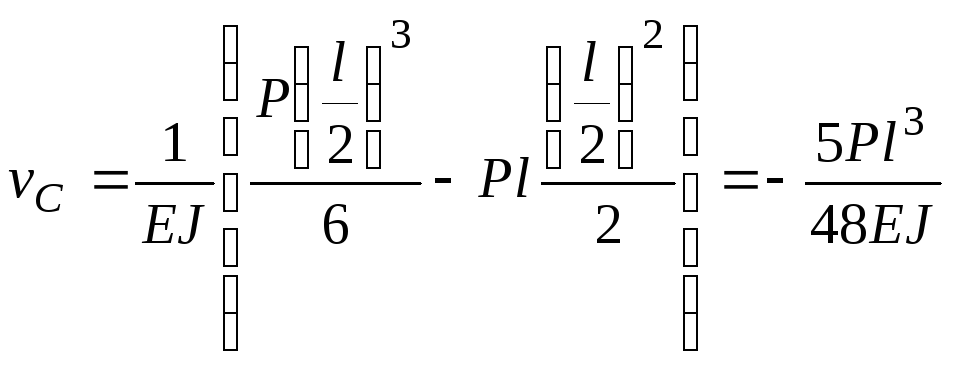при
.
Сравнивая полученные
величины прогибов, приходим к выводу,
что прогиб в сечении В больше, чем прогиб
в сечении С в 3,2 раза:
.
Пример
6.4. В сколько
раз угол
поворота сечения
А
на конце изображенной на рис.6.6 балки
больше, чем угол поворота сечения В на
расстоянии четверти пролета от левого
конца балки?
Решение:
1.
Находим реакции: 
;
.
2.
Выбираем начало координат
на правом конце балки, совмещая его с
точкой А. Ось
направляем вверх, ось
влево.
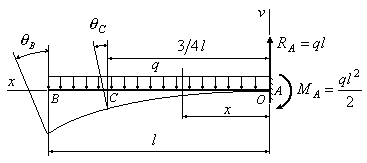
Рис.6.6
3.
Записываем выражение для изгибающего
момента в сечении
:
.
4. Составляем приближенное дифференциальное
уравнение упругой линии балки:
.
Знак
“+”
в уравнении упругой лиинии был принят
потому, что ось
направлена вверх.
5. Принимаем жесткость балки постоянной.
Интегрируем дифференциальное уравнение.
Получаем:
.(д)
Постоянную интегрирования
в уравнении (д) найдем из условия, что
при
угол поворота в сечении А равен нулю.
Подставим в уравнение (д)
и приравняем нулю угол поворота сечения
А. Получим
.
Тогда окончательно уравнение для угла
поворота принимает вид:
.(е)
6.
Подставляем в уравнение (е) координату
,
получим угол поворота в сечении С:
.
7.
Подставляем в уравнение (е) координату
.
Получим угол поворота в сечении В:
.
8. Сравнивая углы
поворота в сечениях В и С, получим:
.
Таким образом,
угол поворота в сечении В в 1,016 раза
больше, чем угол поворота в сечении С.
Пример
6.5.
Найти
стрелу прогиба (в мм) балки, изображенной
на рис.6.7, если жесткость поперечного
сечения балки равна
кНм2.
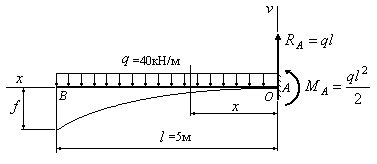
Рис.6.7
Решение:
Воспользуемся
решение задачи, ход которого изложен в
примере 6.4 и проинтегрируем выражение
(д). Получим уравнение для прогиба в
сечении
:
.
(ж)
Постоянные
интегрирования в уравнении (ж) получим,
воспользовавшись граничными усорвиями
закрепления балки, в соответствии с
которыми прогиб и угол поворота в жесткой
заделке равны нулю:
при
и
.
Подставляя
в уравнения (д) и (ж) и приравнивая
последовательно нулю угол поворота и
прогиб нулю, получим:
;
.
Тогда выражение для прогиба принимает
вид:
.
Подставляя
в это уравнение заданные значения
жесткости сечения, интенсивности
распределенной нагрузки, длину балки,
а также координату сечения В, в котором
определяется стрела прогиба (
),
находим:
м
мм.
Знак
“”
у прогиба свидетельствует о том, что
его направление не совпадает с
положительным направлением оси
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
