Как найти угол максимума дифракционной решетки

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

• дифракция на щели (прямоугольном отверстии)
• дифракция на решётке (набор равноотстоящих друг от друга щелей)

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

• для дифракционных максимумов

(1)

• где

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

• для дифракционных минимумов

(2)

• где

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке. 

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Так же, как и для  щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

(3)

Тогда положения максимумов и минимумов дифракции:

• для главных дифракционных максимумов (рис. 3)

(4)

• где

• для дифракционных минимумов

(5)

• где

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):

(6)

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Дифракция на дифракционной решетке

Рассмотрим
дифракцию на одномерной дифракционной
решетке, так как этот вид дифракции
находит широкое применение во многих
методах спектрального анализа.

Дифракционная
решетка представляет собой систему
большого числа одинаковых по ширине и
параллельных друг другу щелей, ле­жащих
в одной плоскости и разделенных
непрозрачными промежутка­ми, равными
по ширине. Изготавливается пу­тем
нанесения параллельных штрихов на
поверхность стекла с помощью делительных
машин. Эти места являются, таким об­разом,
практически непрозрачными промежутками
между неповрежден­ными частями
пластинки, которые играют роль щелей.
Число штрихов на
1 мм
определяется областью спектра исследуемого
излучения –
от
300 мкм
в инфракрасной области до
1200 мкм –
в ультрафиоле­товой).

Итак,
имеется система из N
параллельных щелей с шириной каждой
цели a
и расстоянием между соседними щелями
b
(рис.
2.6). Сумма
a
+ b
= d
называется периодом, или постоянной
дифракцион­ной решетки. На решетку
нормально падает плоская монохроматичес­кая
волна. Требуется исследовать интенсивность
света, распростра­няющегося в
направлении, составляющем угол
φ с нормалью
к пло­скости решетки.

Кроме распределения
ин­тенсивности света вследствие
дифракции на каждой щели, нужно учесть
интерференцию между
N
пучками (пере­распределение световой
энергии за счет интерфе­ренции волн
от N
щелей 
когерентных источников).
Очевидно, минимумы
будут на прежних местах, ибо ус­ловие
минимума дифракции для
всех щелей одинаково. Эти минимумы
называются главными
минимумами.
Они соответствуют таким углам φ
, для которых А_φ
= 0, т.е. свет от разных
частей каждой щели полно­стью гасится.
В этом на­правлении ни одна щель не
дает света. Условие главных
минимумов
совпадает с условием
(2.6).

К
главным минимумам, создаваемым каждой
щелью в от­дельности, добавляются
минимумы, возникающие в результате
интерфе­ренции света, прошедшего
через различные щели. Появляются
добавоч­ные минимумы в областях
дифракционных максимумов. Внешне это
про­является в том, что широкие полосы,
создаваемые одной узкой щелью, покрываются
рядом более тонких полос, вызванных
интерференцией лучей, исходящих от
разных щелей: первой и второй, первой и
треть­ей и т.д. Чем больше щелей, тем
больше добавочных минимумов может
возникнуть. Так как общий световой поток
остается неизменным, про­исходит
усиление световых потоков около
направлений, удовлетворя­вших условиям
максимумов при интерференции от разных
щелей за счет уменьшения световой
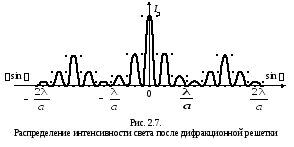
энергии в других направлениях. На рис.
2.7 для примера показано распределение
интенсивности света и расположение
максимумов иминимумов
в случае двух щелей.

Воспользуемся
методом Френеля. В одном и том же
направлении все щели излучают свет
совершенно одинаково. Результат
интерференции зависит от оптической
разности хода в сходственных точках
двух соседних щелей до точки С_–φ,
на экране.
Для всех сходствен­ных точек
эта разность
хода одинакова и равна
d sin
φ. Если

,

(2.7)

колебания
от соседних щелей взаимно усиливают
друг друга, и в точке С_–φ
наблюдается
максимум
ди­фракции. Амплитуда суммарного
колебания в этих точках экрана максимальна:

А_max
≈
NA_φ,

где
A_φ

амплитуда колебания, посылаемого одной
щелью под уг­лом φ.

Интенсивность
главного максимума

,
(2.8)

поэтому
формула
(2.7) определяет
положение главных максимумов
интен­сивности. Число k
дает порядок главного максимума. Максимум
ну­левого порядка один и расположен
в точке С₀;
максимумов первого, второго и т.д.
порядков по два и расположены они
симметрично от­носительно С₀
, на что
указывает знак
“±”.

Кроме
главных максимумов, имеется большое
число более слабых побочных максимумов,
разделенных добавочными
минимумами.
Побочные максимумы значительно слабее
главных
максимумов.
Расчет показывает, что ин­тенсивность
побочных максимумов не превышает
1/23
интенсивности ближайшего главного
максимума. В главных максимумах амплитуда
суммарного колебания в
N
раз, а
интенсивность в
N²
раз больше, чем в соответствующем месте
дает одна щель. Увеличение максимумов
происходит также за счет того, что в
случае решетки отдельные яркие главные
максиму­мы разделены темными областями
добавочных минимумов и очень слабых
побочных максимумов. В итоге происходит
резкое сужение, ди­фракционных
максимумов (пропорционально ~
1/N),
которые стано­вятся тонкими и яркими.
Такие яркие линии, четко локализованные
в пространстве, легко обнаруживаются
и могут быть использованы
для
спектроскопических исследований.

По
мере удаления от центра экрана
интенсивность дифракцион­ных максимумов
убывает (увеличивается расстояние от
источников). Поэтому не удается наблюдать
все возможные дифракционные макси­мумы.

Заметим,
что количество дифракционных максимумов,
даваемых решеткой по одну сторону от
центра экрана, определяется условием
φ = π/2 
максимальный
угол дифракции; sin
φ
< 1, откуда с учетом
(2.8)

.
(2.9)

При
этом не следует забывать, что k

целое число.

Положение
главных максимумов зависит от длины
волны λ.
Поэтому при освещении дифракционной
решетки белым светом все максимумы,
кроме центрального
(k
= 0), разложатся
в спектр, обращенный фиолетовым концом
к центру дифракционной картины. Та­ким
образом, дифракционная решетка может
служить для исследова­ния спектрального
состава света, т.е. для определения
частот (или длин волн) и интенсивности
всех его монохроматических компонент.
Применяемые для этих целей приборы
называются дифракционными спектрографами,
если исследуемый спектр регистрируется
с помощью фотопластинки, и дифракционными
спектроскопами, если спектр на­блюдается
визуально.

Угловая дисперсия
дифракционной решетки

Качество дифракционной решетки
определяется двумя характери­стиками:
угловой дисперсией (D)
и разрешающей силой (разрешающей
спо­собностьюR).

Основное
назначение дифракционной ре­шетки

установление длины волны исследуемого
излучения. Так как положение спектральных
линий задается углом, определяющим
направление лучей (см. уравнение
(2.7)),
целесообразно ввести угловую дисперсию
D:

,
(2.10)

где
∆φ

угловое расстояние между спектральными
линиями, отли­чающимися по длине волны
на ∆λ
(рис.2.8); D

угловое расстояние между двумя линиями,
отличающимися по длине волны на
1
(1=10^-10
м).

Дифференцируя
(2.7)
слева по
φ,
а справа по λ,
находим, что ,
откуда

.

Чем
меньше период решетки d
и чем выше порядок спектра k
, тем больше
угловая дисперсия. В пределах небольших
углов
(cos
φ
~1 )
можно положить

.
(2.11)

Из
выражения
(2.11) следует,
что угловая дисперсия прямо пропорциональна
порядку дифракции k
и обратно
пропорциональна рас­стоянию между
соседними штрихами (периодом решетки)
d
.
Следовательно, для увеличения дисперсии
необходимо увеличивать число штрихов
на единицу длины. Этим объясняется
необходимость изготавливать дифракцион­ные
решетки с возможно большим числом
штрихов на
1 мм
ее ширины.

Разрешающая
сила дифракционной решетки

Большая дисперсия
оптических приборов (в том числе
дифракционной решетки) является
необходимым, но не достаточным условием
для раздельного наблюдения двух
близлежащих линий. В зависимости от
крутизны кривой интенсивности соседние
максимумы длин волн λ₁
и λ₂
могут наблюдаться как два само­стоятельных
или как один максимум. Как видно из рис.
2.9, при одинаковой угловой дисперсии
линий λ₁
и λ₂
возможность их
разре­шения (раздельного восприятия)
различна. Так, на рис. 2.9 слева мини­мум
между линиями λ₁
и λ₂
, отсутствует, и эти линии не разли­чаются
как самостоятельные, а на рис. 2.9
справа имеются наблюдаемые
минимумы между линиями λ₁
и λ₂.

Чтобы
охарактеризовать способность прибора
при данной дис­персии различать две
близлежащие линии, вводится понятие
разре­шающей силы R.
Для количественной характеристики
этого понятия нужно ввести критерий
разрешения. Согласно Рэлею, две близлежащие
спектральные линии с равными интенсивностями
и симметричными одинаковыми контурами
разрешимы, если максимум одной длины
волны λ₁,
совпадает с минимумом дру­гой и
наоборот. При удовлетворении этого
усло­вия интенсивность «провала»
между максимумами составляет
80 %
интенсивности
каждой линии, что является достаточным
для раздель­ного наблюдения линий
λ₁
и λ₂.
Нарушение кри­терия Рэлея приводит
к наблюдению одной линии вместо двух.

Если
разность длин волн | λ₂
– λ₁
| между двумя соседними максимумами,
для которых выполняется критерий Рэлея,
обозначить через ∆λ
, а среднюю
длину волны, соответствующую центру
прова­ла между максимумами,
– через
λ,
то в качестве количественной характеристики
разрешающей силы мож­но взять величину

.
(2.12)

Таким
образом, разрешающей силой R
дифракционной
решетки называется величина, обратная
минимальной раз­ности длин волн ∆λ
(взятой около некоторой длины волны λ),
которые разделены (разрешены) данной
решет­кой. Согласно условию Рэлея, а
также (2.7) разре­шение линий имеет
место при

R
= k
N,

(2.12)

где
k

порядок дифракционного максимума;
N

общее число щелей решетки.

Из
выражения
(2.12) видно,
что чем больше число щелей решетки N
, тем больше
её разрешающая си­ла (разрешающая
способность). При заданном числе щелей
R
увеличивается при переходе к спектрам
высших порядков. Современные дифракционные
решетки обладают до­вольно высокой
разрешающей способностью (до
210⁵
).

Дифракция на
пространственной решетке

Дифракция
света наблюдается не только на плоской
одномерной решетке, но и на двумерной
решетке (штрихи нанесены во взаимно
перпендикулярных направлениях) в одной
и той же плоскости. Но наибольший
практический интерес представляет
дифракция на прост­ранственных
(трехмерных) решетках. В качестве
пространственных дифракционных решеток
могут быть использованы кристаллические
тела (например, монокристаллы), так как
в них неоднородности (ато­мы, ионы)
регулярно повторяются в трех направлениях
(рис. 2.10). Этот случай дифракции привел
Лауэ
(1912 г.) к
открытию метода исследования кристаллов
при помощи дифракции рентгеновских
лучей.

Действительно,
для того, чтобы решетка могла эффективно
разложить излучение в спектр, её
постоянная d
должна быть по порядку ве­личины
примерно такой же, как и длина волны λ.
Для оптической области излучения

это решетка c
периодом d

10^-6 м.
В природе существуют естественные
пространственные структуры с периодом

10^-10 м.
Это
кристаллы,
у которых атомы, ионы или молекулы
расположены упорядоченно и образуют
пространст­венную периодическую
структуру, напоминающую дифракционную
решетку. Период кристаллической решетки
соизмерим с длинами волн рентгеновской
области спектра. Просвечивая кристаллы
рентгеновскими лучами, можно определить
период кри­стал­лической решетки
с по­мощью явления дифракции на
пространственной структуре. Таким
образом, был разработан структурный
анализ кристаллических обра­зова­ний.
С другой стороны, ме­тод Лауэ дал
возможность определять длину волны
рентгеновских лучей, если известна
кристаллическая структура той решетки,
которая слу­жит дифракционной. Метод
явился основой спе­ктроскопии
рентгеновских лучей, позволяющей
установить важнейшие особенности
строения атома.

В
1913 году русский физик
Г.В. Вульф и англичанин У.Л. Брэгг
предложили простой метод расчета
дифракции рентгеновских лучей в
кристаллах. Направления, в которых
получаются дифракционные максимумы,
определяются условием:

,
(2.13)

где
d
– период
структуры, 
– угол скольжения падающих лучей.

Метод позволяет исследовать спект­ральный
состав рентгеновско­го излучения,
если известны расстоя­ния между
отражающими плоскостями ААиВВкристалла
(рентгеновская спектроскопия). И,
наоборот, изучать структуру кристаллов
(определять расстояние между плоскостями,
тип кристаллической решетки и т.д.), если
известна длина волны монохроматического
рентгеновского излучения (рентгеноструктурный
анализ).

ВОПРОСЫ ДЛЯ
САМОКОНТРОЛЯ

1. В чем заключается
   явление дифракции света?

2. При каких условиях
   наблюдается дифракция света?

3. Сущность
   принципа Гюйгенса
   – Френеля.

4. Сущность метода
   зон Френеля. Что такое зона Френеля?

5. Как
   c помощью метода зон Френеля объясняется
   прямолинейное распространение света?

6. При каких условиях
   возникает дифракция Френеля?

7. При каких условиях
   возникает дифракция Фраунгофера?

8. Условия
   образования максимумов и минимумов
   при дифракции от одной щели. Что означает
   величина k
   в формулах максимумов и минимумов
   дифракции?

9. Изобразите
   графически распределение интенсивности
   света на экране при дифракции на одной
   щели. Дайте пояснения.

10. Какой
    вид имеют дифракционные максимумы при
    освещении щели: а) монохроматическим
    светом, б) белым светом? Дайте пояснения.

11. Какое
    устройство называется дифракционной
    решеткой?

12. Перечислите
    характеристики дифракционной решетки.

13. Что
    называют периодом (постоянной)
    дифракционной решетки? Как вычислить
    период дифракционной решетки, зная
    число штрихов на единицу длины?

14. Какую
    величину называют угловой дисперсией
    дифракционной решетки? Как увеличить
    угловую дисперсию дифракционной
    решетки?

15. Какую
    величину называют разрешающей силой
    (разрешающей способностью) дифракционной
    решетки? Как увеличить разрешающую
    способность дифракционной решетки?

16. Напишите
    условия образования главных максимумов
    и главных минимумов при дифракции на
    дифракционной решетке.

17.
В чем преимущества дифракционной решетки
перед щелью?

18.
От каких параметров зависит яркость и
ширина дифракционного максимума при
дифракции на решетке? От чего зависит
общее число дифракционных максимумов,
полученных на экране за решеткой?

19.
Сущность
спектрального анализа. Какие характеристики
определяются с его помощью?

20.Где применяется явление
дифракции рентгеновских лучей? Какие
физические характеристики определяются
с помощью этого явления?

Соседние файлы в папке Уч_Пособие_Часть_3

• #
• #
• #
• #
• #
• #
• #
• #

При перпендикулярном (нормальном) падении параллельного пучка монохроматического света на дифракционную решётку на экране в фокальной плоскости собирающей линзы, расположенной параллельно дифракционной решётке, наблюдается неоднородная картина распределения освещённости разных участков экрана (дифракционная картина).

Главные максимумы этой дифракционной картины удовлетворяют следующим условиям:

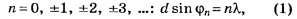
где n — порядок главного дифракционного максимума, d — постоянная (период) дифракционной решётки, λ— длина волны монохроматического света, φ_n— угол между нормалью к дифракционной решётке и направлением на главный дифракционный максимум n-го порядка.

Постоянная (период) дифракционной решётки длиной l

где N — количество щелей (штрихов), приходящихся на участок дифракционной решётки длиной I.

Наряду с длиной волны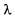часто используется частота v волны.

Для электромагнитных волн (света) в вакууме

где с = 3 *10⁸ м/с — скорость распространения света в вакууме. 

Выделим из формулы (1) наиболее трудно математически определяемые формулы для порядка главных дифракционных максимумов:

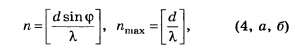
где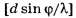 обозначает целую часть числа d*sin(φ/λ).

Недоопределённые аналоги формул (4, а,б) без символа […] в правых частях содержат в себе потенциальную опасность подмены физически обоснованной операции выделения целой части числа 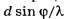операцией округления числа d*sin(φ/λ) до целочисленного значения по формальным математическим правилам.

Подсознательная тенденция (ложный след) подмены операции выделения целой части числа d*sin(φ/λ) операцией округления

этого числа до целочисленного значения по математическим правилам ещё более усиливается, когда речь идёт о тестовых заданиях типа В на определение порядка главных дифракционных максимумов.

В любых тестовых заданиях типа В численные значения искомых физических величин по договорённости округляются до целочисленных значений. Однако в математической литературе нет единых(го) правил(а) округления чисел.

В справочной книге В. А. Гусева, А. Г. Мордковича по математике для учащихся [1] и белорусском учебном пособии Л. А. Латотина, В. Я. Чеботаревского по математике для IV класса [2] приводятся по существу одни и те же два правила округления чисел. В [1] они сформулированы так: “При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяются нулями, а если стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют”.

В справочнике М. Я. Выгодского по элементарной математике [3], выдержавшем двадцать семь (!) изданий, написано (с. 74): “Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится до ближайшего чётного числа, т.е. последняя сохраняемая цифра остаётся неизменной, если она чётная, и усиливается (увеличивается на 1), если она нечётная”.

Ввиду существования различных правил округления чисел следовало бы правила округления десятичных чисел явно сформулировать в “Инструкции для учащихся”, прилагаемой к заданиям централизованного тестирования по физике. Это предложение приобретает дополнительную актуальность, так как в белорусские вузы поступают и проходят обязательное тестирование не только граждане Беларуси и России, но и других стран, и заведомо неизвестно, какими правилами округления чисел они пользовались при обучении в своих странах.

Во всех случаях округление десятичных чисел будем производить по правилам, приведённым в [1], [2].

После вынужденного отступления, возвратимся к обсуждению рассматриваемых физических вопросов.

С учётом нулевого (n = 0) главного максимума и симметричного расположения остальных главных максимумов относительно него общее количество наблюдаемых главных максимумов от дифракционной решётки подсчитывается по формулам:

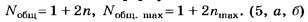
Если расстояние от дифракционной решётки до экрана, на котором наблюдается дифракционная картина, обозначить через Н, то координата главного дифракционного максимума n-го порядка при отсчёте от нулевого максимума равна

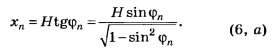
Если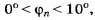 то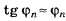 (радиан) 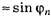и

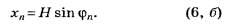
Задачи на рассматриваемую тему часто предлагают на тестированиях по физике.

Начнём обзор с рассмотрения российских тестов, использовавшихся белорусскими вузами на начальном этапе, когда тестирование в Беларуси было необязательным и проводилось отдельными учебными заведениями на свой страх и риск как альтернатива обычной индивидуальной письменно-устной форме проведения вступительных экзаменов.

Тест № 7 [4]

А32. Наибольший порядок спектра, который можно наблюдать при дифракции света с длиной волны λ на дифракционной решётке с периодом d=3,5λ равен

1) 4; 2) 7; 3) 2; 4) 8; 5) 3.

Решение

При освещении дифракционной решётки монохроматическим светом ни о каких спектрах не может быть и речи. В условии задачи речь должна идти о главном дифракционном максимуме наибольшего порядка при перпендикулярном падении монохроматического света на дифракционную решётку.

По формуле (4, б)

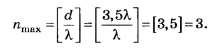
Из недоопределённого условия

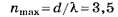
на множестве целых чисел, после округления получаем n_mах=4.

Только благодаря несовпадению целой части числа d/λ с его округлённым целочисленным значением правильное решение (n_mах=3) отличается от неправильного (n_max=4) на тестовом уровне.

Изумительная миниатюра, несмотря на огрехи формулировки, с филигранно выверенным по всем трём версиям округления чисел ложным следом!

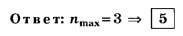
А18. Если постоянная дифракционной решётки d=2 мкм, то для нормально падающего на решётку белого света 400 нм <λ< 700 нм наибольший полностью наблюдаемый порядок спектра равен

1)1; 2)2; 3)3; 4)4; 5)5.

Решение

Очевидно, что n_сп=min(n_1max, n_2max)

По формуле (4, б)

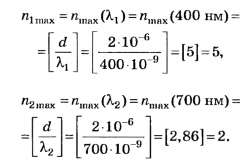
Округляя числа d/λ до целочисленных значений по правилам [1] — [3], получаем:

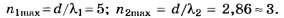
Благодаря тому, что целая часть числа d/λ₂ отличается от его округлённого целочисленного значения, данное задание позволяет на тестовом уровне объективно отличить правильное решение (n_сп=2) от неправильного (n_сп=3). Прекрасная задача с одним ложным следом!

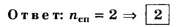
ЦТ 2002 г. Тест № 3 [5]

В5. Найдите наибольший порядок спектра для жёлтой линии Na (λ= 589 нм), если постоянная дифракционной решётки d = 2 мкм.

Решение

Задание сформулировано научно некорректно. Во-первых, при освещении дифракционной решётки монохроматическим светом, как уже отмечалось выше, не может быть и речи о спектре (спектрах). В условии задачи речь должна идти о наибольшем порядке главного дифракционного максимума.

Во-вторых, в условии задания должно быть указано, что свет падает нормально (перпендикулярно) на дифракционную решётку, ибо только этот частный случай рассматривается в курсе физики средних общеобразовательных учреждений. Считать это ограничение подразумевающимся по умолчанию нельзя: в тестах все ограничения должны быть указаны явно! Тестовые задания должны представлять собою самодостаточные, научно корректные задания.

С учётом вышеприведённых уточнений

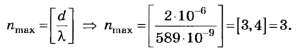
Число 3,4, округлённое до целочисленного значения по правилам арифметики [1] — [3], также даёт 3. Именно поэтому данное задание следует признать простым и, по большому счёту, неудачным, так как на тестовом уровне оно не позволяет объективно различить правильное решение, определяемое по целой части числа 3,4, от неправильного решения, определяемого по округлённому целочисленному значению числа 3,4. Различие обнаруживается только при подробном описании хода решения, что и сделано в данной статье.

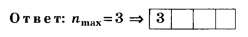
Дополнение 1. Решите вышеприведённую задачу, заменив в её условии d=2 мкм на d=1,6 мкм. Ответ: n_max = 2.

ЦТ 2002 г. Тест 4 [5]

В5. На дифракционную решётку направляется свет от газоразрядной лампы. На экране получаются дифракционные спектры излучения лампы. Линия с длиной волны λ₁= 510 нм в спектре четвёртого порядка совпадает с линией длины волны λ₂ в спектре третьего порядка. Чему равна λ₂(в [нм])?

Решение

В данной задаче основной интерес представляет не решение задачи, а формулировка её условия.

При освещении дифракционной решётки немонохроматическим светом(λ₁, λ₂) вполне естественно говорить (писать) о дифракционных спектрах, которых в принципе нет при освещении дифракционной решётки монохроматическим светом.

В условии задания следовало бы указать, что свет от газоразрядной лампы падает нормально на дифракционную решётку.

Кроме того, следовало бы изменить филологический стиль третьего предложения в условии задания. Режет слух оборот “линия с длиной волны λ^”, его можно было бы заменить на “линия, соответствующая излучению длиной волны λ^” или на более краткий — “линия, соответствующая длине волны λ^”.

Формулировки тестов должны быть научно корректными и литературно безупречными. Тесты формулируют совсем не так, как исследовательские и олимпиадные задачи! В тестах всё должно быть точно, конкретно, однозначно.

С учётом приведённого уточнения условия задания имеем:

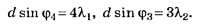
Так как по условию задания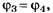то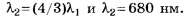

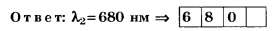
ЦТ 2002 г. Тест № 5 [5]

В5. Найдите наибольший порядок дифракционного максимума для жёлтой линии натрия с длиной волны 5,89·10^-7 м, если период дифракционной решётки равен 5 мкм.

Решение

По сравнению с заданием В5 из теста № 3 ЦТ 2002 г. данное задание сформулировано точнее, тем не менее в условии задания речь следовало бы вести не о “дифракционном максимуме”, а о “главном дифракционном максимуме“.

Наряду с главными дифракционными максимумами всегда имеются ещё и вторичные дифракционные максимумы [6, с. 617, 618]. Не объясняя этого нюанса в школьном курсе физики, тем более надо строго соблюдать сложившуюся научную терминологию и вести речь только о главных дифракционных максимумах.

Кроме того, следовало бы указать, что свет падает нормально на дифракционную решётку.

С учётом вышеприведённых уточнений

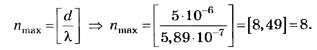
Из неопределённого условия

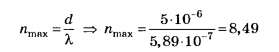
по правилам математического округления числа 8,49 до целочисленного значения опять же получаем 8. Поэтому данное задание, как и предыдущее, следует признать неудачным.

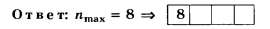
Дополнение 2. Решите вышеприведённое задание, заменив в его условии d=5 мкм на (1=А мкм. Ответ: n_max=6.)

---

Пособие РИКЗ 2003 г. Тест № 6 [7]

В5. Если второй дифракционный максимум находится на расстоянии 5 см от центра экрана, то при увеличении расстояния от дифракционной решётки до экрана на 20% этот дифракционный максимум будет находиться на расстоянии … см.

Решение

Условие задания сформулировано неудовлетворительно: вместо “дифракционный максимум” надо “главный дифракционный максимум”, вместо “от центра экрана” — “от нулевого главного дифракционного максимума”.

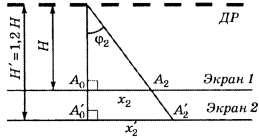
Как видно из приведённого рисунка,

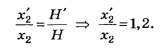
Отсюда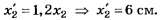

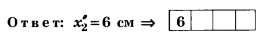
Пособие РИКЗ 2003 г. Тест № 7 [7]

В5. Определите наибольший порядок спектра в дифракционной решётке, имеющей 500 штрихов на 1 мм, при освещении её светом с длиной волны 720 нм.

Решение

Условие задания сформулировано крайне неудачно в научном отношении (см. уточнения заданий № 3 и 5 из ЦТ 2002 г.).

Есть претензии и к филологическому стилю формулировки задания. Вместо словосочетания “в дифракционной решётке” надо было бы использовать словосочетание “от дифракционной решётки”, а вместо “свет с длиной волны” — “светом, длина волны которого”. Длина волны — не нагрузка к волне, а её основная характеристика.

С учётом уточнений

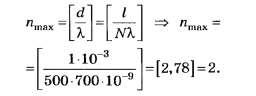
По всем трём вышеприведённым правилам округления чисел округление числа 2,78 до целочисленного значения даёт 3.

Последний факт даже при всех недостатках формулировки условия задания делает его интересным, так как позволяет на тестовом уровне различить правильное (n_max=2) и неправильное (n_max=3) решения.

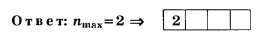
Много заданий на рассматриваемую тему содержится в ЦТ 2005 г. [8].

В условиях всех этих заданий (В1) надо добавить ключевое слово “главный” перед словосочетанием “дифракционный максимум” (см. комментарии к заданию В5 ЦТ 2002 г. Тест № 5).

К сожалению, во всех вариантах тестов В1 ЦТ 2005 г. численные значения d (l,N) и λ подобраны неудачно и всегда дают в дробях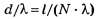

число “десятых” меньше 5, что не позволяет на тестовом уровне отличить операцию выделения целой части дроби (правильное решение) от операции округления дроби до целочисленного значения (ложный след). Это обстоятельство ставит под сомнение целесообразность использования этих заданий для объективной проверки знаний абитуриентов по рассматриваемой теме.

Похоже на то, что составители тестов увлеклись, образно говоря, приготовлением различных “гарниров к блюду”, не думая об улучшении качества основной компоненты “блюда” — подборе численных значений d (l,N) и λ с целью увеличения числа “десятых” в дробях d/λ=l/(N*λ).

ЦТ 2005 г. Вариант 4 [8]

В1. На дифракционную решётку, период которой d₁=1,2 мкм, падает нормально параллельный пучок монохроматического света с длиной волны λ=500 нм. Если её заменить на решётку, период которой d₂=2,2 мкм, то число максимумов увеличится на … .

Решение

Вместо “свет с длиной волны λ” надо “свет длиной волны λ” . Стиль, стиль и ещё раз стиль!

Так как

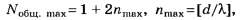
то с учётом того, что X — const, a d₂>di,

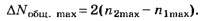
По формуле (4, б)

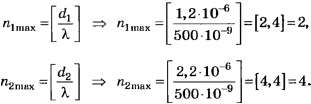
Следовательно, ΔN_{общ. max}=2(4-2)=4

При округлении чисел 2,4 и 4,4 до целочисленных значений тоже получаем соответственно 2 и 4. По этой причине данное задание следует признать простым и даже неудачным.

Дополнение 3. Решите вышеприведённую задачу, заменив в её условии λ=500 нм на λ=433 нм (синяя линия в спектре водорода).

Ответ: ΔN_{общ. max}=6

ЦТ 2005 г. Вариант 6

В1. На дифракционную решётку с периодом d= 2 мкм падает нормально параллельный пучок монохроматического света с длиной волны λ=750 нм. Количество максимумов, которые можно наблюдать в пределах угла а=60°, биссектриса которого перпендикулярна плоскости решётки, равно … .

Решение

Словосочетание “света с длиной волны λ” уже обсуждалось выше в ЦТ 2005 г., вариант 4.

Второе предложение в условии данного задания можно было бы упростить и записать так: “Количество наблюдаемых главных максимумов в пределах угла а = 60°” и далее по тексту исходного задания.

Очевидно, что

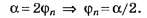
По формуле (4, а)

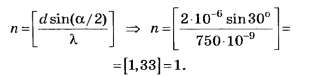
По формуле (5, а)

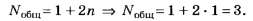
Это задание, как и предыдущее, не позволяет на тестовом уровне объективно определить уровень понимания обсуждаемой темы абитуриентами.

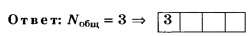
Дополнение 4. Выполните вышеприведённое задание, заменив в его условии λ=750 нм на λ= 589 нм (жёлтая линия в спектре натрия). Ответ: N_o6щ=3.

ЦТ 2005 г. Вариант 7

В1. На дифракционную решётку, имеющую N₁– 400 штрихов на l=1 мм длины, падает параллельный пучок монохроматического света с длиной волны λ=400 нм. Если её заменить решёткой, имеющей N₂=800 штрихов на l=1 мм длины, то количество дифракционных максимумов уменьшится на … .

Решение

Опустим обсуждение неточностей формулировки задания, так как они те же, что и в предыдущих заданиях.

Из формул (4, б), (5, б) следует, что

Следовательно,

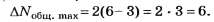
Комментарии о качестве данного задания опустим, “рука… колоть устала”!

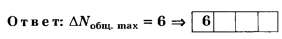
Дополнение 5. Решите вышеприведённую задачу, заменив в её условии λ=400 нм на λ=461 нм (голубая линия в спектре стронция). Ответ: ∆N=6.

ЦТ 2005 г. Вариант 8

В1. На дифракционную решётку с d=1 мкм падает нормально параллельный пучок монохроматического света. Если длина волны света λ=400 нм, то число максимумов, которые образует эта решётка, равно … .

Решение

Злополучное “с” уже перекочевало от “света с длиной волны” к “решётке с d=1 мкм”. Появилось и новое жаргонное выражение — “число максимумов, которые образует эта решётка”. Сама по себе “решётка” не образует дифракционной картины, поэтому следовало бы написать “количество главных максимумов, образованных освещённой решёткой, равно…”.

По формулам (5, б), (4, б)

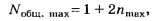
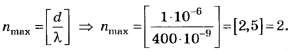
По версии округления чисел [1], [2] целочисленное значение числа 2,5 равно 3, а по версии М. Я. Выгодского [3] — 2.

В сравнении с российским заданием А32 из № 7 Тестов по физике [4], которое рассмотрено выше, данный белорусский тест является ущербным, но на фоне белорусских тестов ЦТ 2005 г. на рассматриваемую в данной статье тему он является лучшим, несмотря на неточности его формулировки.

Итак, N_{общ. max}=1+2*2=5 а по версии округления чисел [1], [2] N_{общ. max}= 1+2*3 =7 (ложный след).

Благодаря этому ложному следу, данное задание в рамках версии округления чисел [1], [2] позволяет на тестовом уровне отличить правильное решение (N_{общ. max}=5) от неправильного (N_{общ. max}=7).

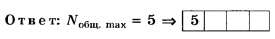
ЦТ 2008 г. Вариант 1 [9]

В12. На дифракционную решётку нормально падает параллельный пучок монохроматического света длиной волны λ=720 нм. Если период решётки d = 5 мкм, то максимальный порядок k_max дифракционного спектра … .

Решение

Задание сформулировано научно некорректно (см. условия предыдущих заданий), но численные значения величин d и λ подобраны удачно и на тестовом уровне правильное решение, определяемое по целой части числа, отличается от неправильного решения, определяемого по округлённому целочисленному значению числа d/λ

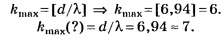
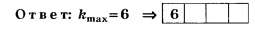
Задания В12 из других вариантов тестов ЦТ 2008 г. предлагаю читателям рассмотреть самостоятельно.

Вывод

За многие годы проведения централизованных тестирований по физике так и не созданы качественные задания на определение порядка главных дифракционных максимумов при перпендикулярном освещении дифракционной решётки монохроматическим светом: то ли условия заданий были сформулированы некорректно, то ли численные значения величин d(l, N) и X были подобраны неудачно и не позволяли на тестовом уровне отличить правильное решение от неправильного.

Список использованной литературы

1. Математика: справочные материалы: кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — Москва : Просвещение, 1988.

2. Математика: учеб. пособие для 4-го класса общеобр. школы с рус. яз. обуч. / Л. А. Лату-тин, В. Д. Чеботаревский; пер. с бел. яз. Т. В. Водневой. — 2-е изд. — Минск : Нар. асвета, 2002.

3. Справочник по элементарной математике. — 27-е изд., испр. / М. Я. Выгодский. — Москва : Наука, 1986.

4. Тесты по физике. 11 кл. / Центр тестирования Министерства образования России. — Москва : Просвещение, 2001.

5. Тесты. Физика. Русский язык: варианты и ответы централизованного тестирования: пособие для подготовки к тестированию / Респ. ин-т контроля знаний. — Минск : Асар, 2003.

6. Справочник по физике для инженеров и студентов вузов. — 6-е изд., испр. / Б. М. Яворский, А. А. Детлаф. — Москва : Наука, 1974.

7. Тесты: Физика. Материалы для подготовки к централизованному тестированию / Респ. ин-т контроля знаний. — Мозырь : Белый Ветер, 2003.

8. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Юнипресс, 2005.

9. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Аверсэв, 2008.

Как определить угол дифракции

Световые волны отклоняются от своего прямолинейного пути при прохождении через малые отверстия или мимо таких же малых препятствий. Это явление возникает, когда размеры препятствий или отверстий сравнимы с длиной волны, и называется дифракцией. Задачи на определение угла отклонения света приходится решать чаще всего применительно к дифракционным решеткам – поверхностям, в которых чередуются прозрачные и непрозрачные участки одинаковых размеров.

Инструкция

Выясните период (d) дифракционной решетки – так называют суммарную ширину одной прозрачной (a) и одной непрозрачной (b) ее полос: d = a+b. Эту пару обычно называют одним штрихом решетки, а измеряют в количестве штрихов на один миллиметр. Например, дифракционная решетка может содержать 500 штрихов на 1 мм, и тогда d = 1/500.

Для вычислений имеет значение угол (α), под которым свет падает на дифракционную решетку. Он отсчитывается от нормали к поверхности решетки, а в формуле участвует синус этого угла. Если в исходных условиях задачи сказано, что свет падает по нормали (α=0), этой величиной можно пренебречь, так как sin(0°)=0.

Выясните длину волны (λ) падающего на дифракционную решетку света. Это одна из наиболее важных характеристик, определяющих угол дифракции. Нормальный солнечный свет содержит целый спектр длин волн, но в теоретических задачах и лабораторных работах, как правило, речь идет о точечном участке спектра – о «монохроматическом» свете. Видимой области соответствуют длины примерно от 380 до 740 нанометров. Например, один из оттенков зеленого цвета имеет длину волны, равную 550нм (λ=550).

Прошедший через дифракционную решетку свет отклоняется на разные углы, образуя при этом неоднородную картину распределения с чередующимися максимумами и минимумами освещенности – дифракционный спектр. Каждому максимуму соответствует собственный угол дифракции. Выясните: угол которого максимума (k) требуется рассчитать. Отсчет ведется от нулевого – центрального – уровня. Например, условия могут требовать расчета искомой величины для второго (k=2) максимума дифракционного спектра.

Воспользуйтесь формулой, связывающей длину волны падающего на дифракционную решетку света с углом дифракции (φ) максимумов определенного порядка: d*(sin(φ)-sin(α)) = k*λ. Выведите из нее определение угла φ – у вас должно получиться такое равенство: φ = arcsin(sin(α)+(k*λ)/d). Подставьте определенные на предыдущих шагах значения в эту формулу и произведите расчеты.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?