Как найти угол между биссектрисами внешних углов

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

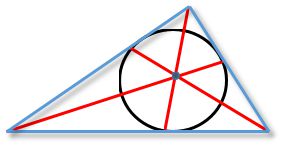
Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

• CD – внутренняя биссектриса ∠ACB;
• CE – биссектриса угла, смежного с ∠ACB;
• ∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

Биссектриса внешнего угла треугольника

Чему равен угол, который образует биссектриса внешнего угла треугольника с биссектрисой смежного ему внутреннего угла?

Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.

Дано: ∆ ABC,

∠BAP — внешний угол при вершине A,

AN — биссектриса ∠BAP,

AM — биссектриса ∠BAC.

Доказательство: (аналогично доказательству об угле между биссектрисами смежных углов).

Так как внешний угол треугольника — это угол, смежный с внутренним углом при данной вершине, то по свойству смежных углов

Так как AN — биссектриса внешнего угла BAP, то

Так как AM — биссектриса угла BAC, то

Итак, мы доказали, что биссектриса внешнего угла треугольника образует с биссектрисой внутреннего угла при данной вершине прямой угол:

Вывод: если требуется найти угол между биссектрисами внешнего и внутреннего углов треугольника, знать градусные меры самих углов не требуется. Каким бы ни был внешний угол треугольника, его биссектриса перпендикулярна биссектрисе смежного внутреннего угла.

4 Comments

докажите что биссектриса внешнего угла противоположного основанию равнобедренного треугольника параллельна основатию этого угла

Решите пожалуйста. Один из углов треугольника равен альфа. Найдите угол между биссектрисами внешних углов, проведённых из вершин двух других углов.

Элементы треугольника. Биссектриса

Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.

Свойства биссектрисы

1. Биссектриса треугольника делит угол пополам.

2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()

3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.

4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.

Некоторые формулы, связанные с биссектрисой треугольника

(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне ,
— стороны треугольника против вершин соответственно,
— длины отрезков, на которые биссектриса делит сторону ,

Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.

Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1

Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы

Чтобы не потерять страничку, вы можете сохранить ее у себя:

[spoiler title=”источники:”]

[/spoiler]

См. также биссектриса угла.

БИССЕКТРИСА УГЛА ТРЕУГОЛЬНИКА

Биссектриса треугольника – отрезок биссектрисы угла, соединяющий вершину этого угла с точкой на противолежащей стороне.

У биссектрис угла треугольника есть масса свойств, которые описываются через свойства треугольника. Это поможет в решении задач.

Свойства биссектрис треугольника

• Биссектриса треугольника, проведенная из данной вершины, тождественна биссектрисе соответствующего угла. Биссектриса угла треугольника, выходящая из его вершины, делит этот угол треугольника пополам 

• Все три биссектрисы треугольника пересекаются в одной точке, которая расположена всегда в плоскости треугольника и является центром вписанной окружности. Примечание. Имеются ввиду биссектрисы внутренних углов треугольника.
  

Свойства биссектрис равнобедренного треугольника

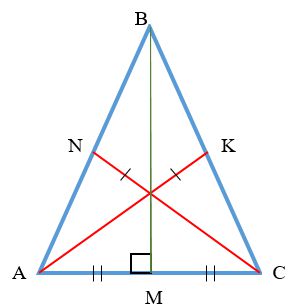
• У равнобедренного треугольника медиана, биссектриса и высота, проведенные к основанию треугольника, совпадают

• Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.

• В равнобедренном треугольнике две биссектрисы равны, а третья биссектриса является его медианой и высотой
  

• Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный

Свойства биссектрис равностороннего треугольника

• У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам

• У равностороннего треугольника все три внутренние биссектрисы равны
• У равностороннего треугольника все три «замечательные» линии (высота, биссектриса и медиана) совпадают и три «замечательных» точки (точки ортоцентра, центра тяжести и центра вписанной и описанной окружностей) находятся в одной точке пересечения «замечательных» линий, т.е. тоже совпадают.

Формулы нахождения биссектрисы угла

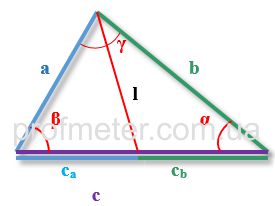
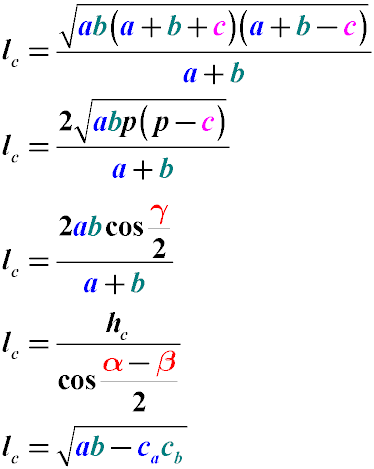
a, b, c – стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
α,β,γ – углы треугольника, противолежащие сторонам a,b,c соответственно
p – полупериметр треугольника (половина суммы всех его сторон)
c_a, c_b – отрезки, на которые биссектрисой, проведенной из угла c разбита сторона c

l_c – длина биссектрисы, проведенной к стороне c из угла γ.

Длина биссектрис треугольника может быть выражена через равенство с квадратом суммы всех его сторон.

Формулы нахождения расстояния от угла до точки пересечения биссектрис

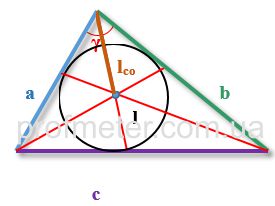
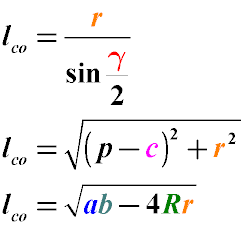
где

l_co – длина отрезка, лежащего на биссектрисе от вершины угла до центра пересечения биссектрис
r – радиус окружности, вписанной в треугольник
R – радиус описанной окружности
a, b, c – стороны треугольника, при этом биссектриса проведена из угла, находящегося между сторонами a, b
γ – угол треугольника, противолежащий стороне c 
p – полупериметр треугольника (половина суммы всех его сторон) 

Примеры решения задач

Примечание. В данном уроке изложены задачи по геометрии о биссектрисе. Если Вам необходимо решить задачу по геометрии, которой здесь нет – пишите об этом в форуме. Почти наверняка курс будет дополнен.

Задача.

Луч AD является биссектрисой угла A. На сторонах угла A отмечены точки B,C так что угол ADC равен углу ADB. Доказать, что AB=AC.

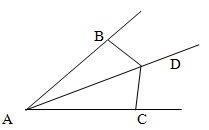
Решение.
Рассмотрим треугольники ADB и ADC. Сторона AD у них общая, углы DAC и DAB равны, так как биссектриса AD делит угол А пополам, а углы ADC и ADB равны по условию задачи. Таким образом, треугольники ADB и ADC равны по стороне и двум углам.

Следовательно AB = AC.

0
 

 Биссектриса угла |

Описание курса

| Биссектриса внешнего угла 

Чему равен угол, который образует биссектриса внешнего угла треугольника с биссектрисой смежного ему внутреннего угла?Утверждение.Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.bissektrisa vneshnego ugla treugolnika Дано: ∆ ABC,∠BAP — внешний угол при вершине A,AN — биссектриса ∠BAP,AM — биссектриса ∠BAC.Доказать: ∠MAN=90º.Доказательство: (аналогично доказательству об угле между биссектрисами смежных углов).Так как внешний угол треугольника — это угол, смежный с внутренним углом при данной вершине, то по свойству смежных углов[angle BAP + angle BAC = {180^o}.]Так как AN — биссектриса внешнего угла BAP, то[angle BAN = frac{1}{2}angle BAP.]Так как AM — биссектриса угла BAC, то[angle BAM = frac{1}{2}angle BAC.]Таким образом,[angle MAN = angle BAN + angle BAM = ][ = frac{1}{2}angle BAP + frac{1}{2}angle BAC = ][ = frac{1}{2}(angle BAP + angle BAC) = frac{1}{2} cdot {180^o} = {90^o}.]svoystvo bissektrisyi vneshnego ugla treugolnika Итак, мы доказали, что биссектриса внешнего угла треугольника образует с биссектрисой внутреннего угла при данной вершине прямой угол:[AM bot AN.]Вывод: если требуется найти угол между биссектрисами внешнего и внутреннего углов треугольника, знать градусные меры самих углов не требуется. Каким бы ни был внешний угол треугольника, его биссектриса перпендикулярна биссектрисе смежного внутреннего угла

Оцени ответ

• Комментировать
• Жалоба
• Ссылка