Многогранник, одна грань которого является (n)-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, (n)-угольник называется основанием пирамиды, а треугольники — боковыми гранями.
Общая вершина боковых граней называется вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.
Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок:
1. первым рисуется основание,
2. по условию задачи находится проекция вершины на плоскости основания,
3. вертикально проводится высота,
4. проводятся рёбра.
На рисунке изображена четырёхугольная пирамида (SABCD)
(первой пишут букву вершины).
Основание — четырёхугольник (ABCD).
Вершина проецируется в точку пересечения диагоналей (O) — основание высоты или проекция вершины.
(SA), (SB), (SC), (SD) — рёбра пирамиды,
(AB), (BC), (CD), (DA) — стороны основания.
В курсе средней школы в основном есть задачи, в которых даны:
– правильная пирамида (вершина проецируется в центр основания);
– пирамида, вершина которой проецируется в центр описанной окружности;
– пирамида, вершина которой проецируется в центр вписанной окружности;
– пирамида, высота которой совпадает с боковым ребром;
– пирамида, высота которой также является высотой боковой грани.
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды.
Двугранный угол между боковой гранью (SCD) и гранью основания равен линейному углу
∠
(OES). Этот угол образован отрезками (OE) и (SE), лежащими в этих гранях и перпендикулярных их общей прямой (CD). То есть (OE)
⊥CD
и (SE)
⊥CD
.
Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах.
Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания.
На рисунке
∠
(OCS).
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды.
Основные формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды:
S=S1+S2+S3+…
(Некоторые формулы годятся только для определённых видов пирамиды.)
Площадь полной поверхности
Sп.п.=S+Sоснования
.
Объём пирамиды (V =)
13Sоснования
(H), где (H) — высота пирамиды.
Формула объёма используется для пирамид любого вида.
Источники:
Рис. 1. Пирамида, © ЯКласс.
Косинус угла между боковой гранью и основанием правильной треугольной пирамиды равен Найдите угол между боковыми гранями этой пирамиды.
Спрятать решение
Решение.
Пусть SABC — данная пирамида с вершиной S, SH — ее высота, M — середина BC, CK — высота треугольника
Угол SMH — угол между боковой гранью пирамиды и основанием.
Пусть тогда
Найдем площадь треугольника двумя способами:
Значит,
Ребро AC перпендикулярно плоскости SBH, поэтому SB и AC перпендикулярны, следовательно, плоскость AKC перпендикулярна ребру Искомый угол между боковыми гранями равен углу при вершине равнобедренного треугольника
Ответ:
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получен верный ответ | 2 |
| Решение содержит обоснованный переход к планиметрической задаче, но получен неверный ответ или решение не закончено
ИЛИ при правильном ответе решение недостаточно обосновано |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, – это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.
Пространственная фигура пирамида
Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово “пирамида”. Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.
Двугранные углы фигуры
Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.
Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:
- При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n – число сторон многоугольника.
- Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.
Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип – на боковых ребрах.
Как рассчитать углы пирамиды?
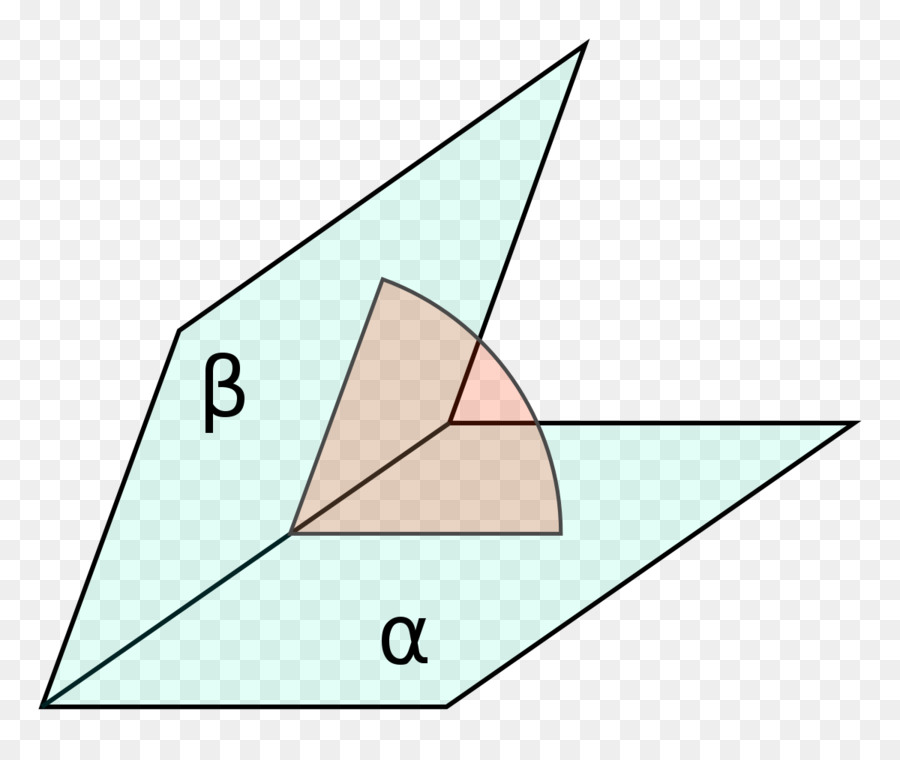
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.
В трехмерном пространстве плоскость задается следующим выражением:
A*x + B*y + C*z + D = 0
Где A, B, C, D – это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:
n¯ = [A; B; C]
Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.
Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:
n1¯ = [A1; B1; C1];
n2¯ = [A2; B2; C2]
Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:
φ = arccos(|(n1¯*n2¯)|/(|n1¯|*|n2¯|))
Или в координатной форме:
φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))
Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.
Углы правильной пирамиды четырехугольной
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.
Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.
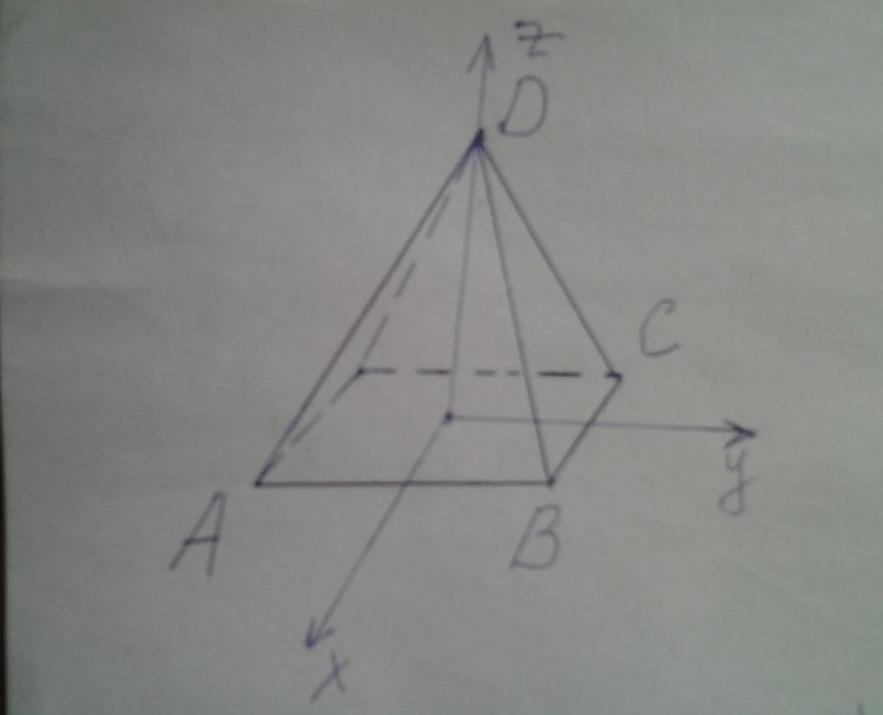
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:
A(a/2; -a/2; 0);
B(a/2; a/2; 0);
C(-a/2; a/2; 0);
D(0; 0; h)
Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:
Для ABC:
AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n1¯ = [AB¯*AC¯] = (0; 0; a2)
Для ABD:
AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n2¯ = [AB¯*AD¯] = (a*h; 0; a2/2)
Для BCD:
BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n3¯ = [BC¯*BD¯] = (0; a*h; a2/2)
Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:
Угол между ABC и ABD:
(n1¯*n2¯) = a4/2; |n1¯| = a2; |n2¯| = a*√(h2 + a2/4);
φ = arccos(a4/2/(a2*a*√(h2 + a2/4))) = arccos(a/(2*√(h2 + a2/4))) = 67,38o
Угол между ABD и BDC:
(n2¯*n3¯) = a4/4; |n2¯| = a*√(h2 + a2/4) ; |n3¯| = a*√(h2 + a2/4);
φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o
Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.
Углы треугольной правильной пирамиды
На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.
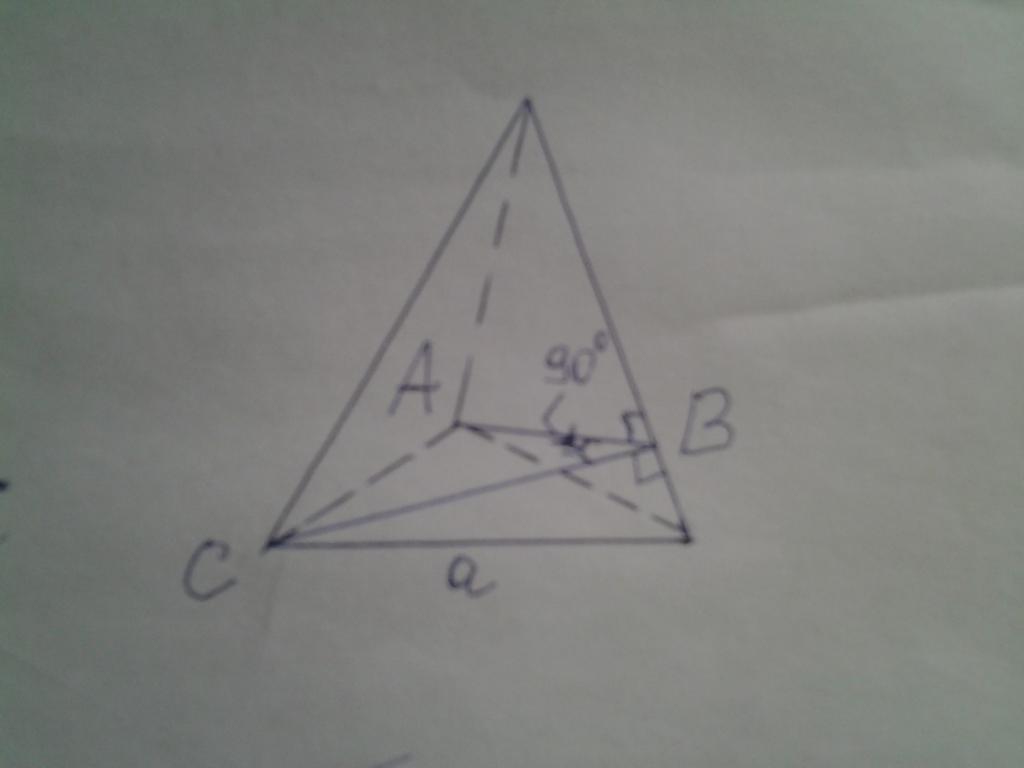
Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры – h, апофему – hb и боковое ребро – b. Теперь можно записать следующие формулы:
S = 1/2*a*hb;
b2 = hb2 + a2/4;
b2 = h2 + a2/3
Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:
x = a/√2;
S = 1/2*b*a/√2
Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:
1/2*a*hb = 1/2*b*a/√2 =>
hb = b/√2;
b2 = b 2/2 + a2/4 =>
b = a/√2;
a2/2 = h2 + a2/3 =>
a = h*√6
Площадь равностороннего треугольника рассчитывается так:
S = √3/4*a2 = 3*√3/2*h2
Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.
|
Можно ли примитивным способом, пусть не совсем точно, вычислить угол между боковыми гранями пирамиды, в основании которой лежит параллелепипед? Нужно для практического использования…. Измерить можем только длинны (рулеткой), углы измерить точно – нереально… Углы треугольников можно несложно посчитать… А вот угол между гранями (боковыми), проблема… Есть ли формула расчёта, которую можно использовать на ходу, с калькулятором телефона? Если основание пирамиды прямоугольник (не параллепипед) и боковые грани равнобедренные треугольники, то можно вывести общую формулу для вычисления угла между гранями и основанием. Измеряя длины ребер (стороны треугольников) можно найти высоту каждого треугольника (апофему). Пусть это будет с – гипотенуза прямоугольного треугольника. Измеряя длину и ширину прямоугольника и деля его пополам можно найти катет этого треугольника а. Тогда по формуле sin x = a/c можно найти искомый угол х (через арксинус, который есть в калькуляторе). Знаете ответ? |
2.5. Пирамида. Правильная пирамида
Одним из важнейших видов многогранников являются пирамиды, с которыми вы уже неоднократно встречались. Любой школьник наверняка сможет отличить пирамиду от многогранника иного вида. Но лишь в этом параграфе даётся формальное определение понятия «пирамида».
Определение 18
n-Угольной пирамидой называется многогранник, имеющий n + 1 грань (т. е. n + 1-гранник), причём одна грань у него — n-угольник, а n оставшихся граней — треугольники с общей вершиной.
n-Угольная грань n-угольной пирамиды называется основанием, а все прочие треугольные грани называются боковыми гранями. Общую для боковых граней вершину называют вершиной пирамиды. Рёбра пирамиды, выходящие из вершины, называют боковыми рёбрами пирамиды.
Простейший многогранник — четырёхгранник или тетраэдр — это также и простейшая пирамида — треугольная. Особенность треугольной пирамиды состоит в том, что любую грань можно рассматривать как основание. (Три другие грани являются соответственно боковыми гранями.) Именно разумный выбор основания может быть залогом успеха решения некоторых задач.
Приведём две полезные теоремы.
Теорема 2.4 (свойство пирамиды с равными боковыми рёбрами)
Если боковые рёбра пирамиды равны между собой, то в основании этой пирамиды лежит многоугольник, около которого можно описать окружность. При этом вершина пирамиды проектируется в центр описанной около основания окружности.

Рис. 58
Доказательство. Утверждение теоремы следует из того, что равные наклонные имеют равные проекции. Пусть S — вершина пирамиды, A и B — две какие-то вершины основания, O — проекция S на плоскость основания (рис. 58). Треугольники SAO и SBO — прямоугольные (∠ SOA = ∠ SBO = 90°) с общим катетом SO и равными по условию гипотенузами: SA = SB. Значит , OA = OB. Таким образом, точка O равноудалена от всех вершин основания.
Теорема доказана. ▼
Теорема 2.5 (свойство пирамиды с равными углами между основанием и боковыми гранями)
Если все углы между плоскостями боковых граней и плоскостью основания равны между собой (иными словами, боковые грани наклонены к плоскости основания под равными углами), то все прямые, на которых лежат стороны основания, касаются одной окружности, а вершина пирамиды проектируется в центр этой окружности.

Рис. 59
Доказательство. Пусть S — вершина пирамиды, O — проекция S на плоскость основания, AB — какая-то сторона основания, K — проекция S на прямую AB, a — угол между плоскостью основания и плоскостями боковых граней. По определению a ⩽ 90° (в данном случае a ≠ 90°, рис. 59, а); ∠ SKO = a — линейный угол соответствующего двугранного угла. Если SO = h, то OK = SO ctg ∠ SKO = h ctg a. Таким же будет расстояние от O до всех сторон основания. ▼
Замечание. Обратите внимание на то, что в условии теоремы говорится об углах между парами плоскостей — плоскостью основания и плоскостями боковых граней. Утверждение теоремы будет тем более верным, если равны двугранные углы при основании, т. е. двугранные углы, рёбрами которых служат стороны основания и одна из граней которых — полуплоскость, содержащая боковую грань, а другая — полуплоскость, содержащая основание пирамиды. В этом случае вершина проектируется непременно внутрь основания (в случае равенства двугранных углов при основании все эти углы непременно острые), в то время как при условиях, сформулированных в теореме, проекция вершины может оказаться и вне основания (рис. 59, б). Итак, мы можем уточнить утверждение теоремы 2.5.
Если в основании пирамиды лежит выпуклый многоугольник и все двугранные углы при основании равны, то основанием является описанный многоугольник, а вершина проектируется в центр вписанной в основание окружности.
Отрезок SO (S — вершина, O — проекция S на плоскость основания) называется высотой пирамиды, O — основание высоты. Нетрудно теперь переформулировать теоремы 2.3 и 2.4 с использованием терминов «высота пирамиды» и «основание высоты».
В следующей теореме формулируется общее свойство произвольных пирамид.
Теорема 2.6 (свойство параллельных сечений пирамиды)
Сечением пирамиды плоскостью, параллельной основанию, является многоугольник, подобный основанию.

Рис. 60
Доказательство. Докажем, что все углы в сечении равны соответствующим углам основания, а стороны сечения пропорциональны соответствующим сторонам основания. Заметим, что достаточно это сделать для двух соседних сторон основания и соответствующих им сторон сечения.

Пусть A, B, C — три последовательные вершины основания, S — вершина пирамиды, A1, B1, C1 — точки, в которых плоскость, параллельная основанию, пересекает рёбра SA, SB и SC соответственно (рис. 60). Так как A1B1 ‖ AB и B1C1 ‖ BC, то ∠ A1B1C1 = ∠ ABC (см. теорему 1.8). Кроме того, из подобия пар треугольников SA1B1 и SAB, SB1C1 и SBC получаем: A1B1 : AB = SB1 : SB = B1C1 : BC. ▼
Среди множества пирамид выделяется один важный тип пирамид: правильные пирамиды.
Определение 19
Пирамида называется правильной, если в основании её лежит правильный многоугольник, а все боковые рёбра равны между собой.
Приведём определение правильного тетраэдра.
Правильным называется тетраэдр (т. е. треугольная пирамида), у которого все рёбра равны между собой.
Понятно, что правильная треугольная пирамида и правильный тетраэдр — это не одно и то же.
|
|
|
1(в). Все боковые рёбра пирамиды равны b, а высота равна h. Чему равен радиус описанной около основания окружности? |
|
2(в). Найдите двугранные углы правильного тетраэдра. |
|
3(в). Найдите высоту правильного тетраэдра с ребром a. |
|
4.Сколько существует различных пирамид, все рёбра которых равны l ? |
|
5(в). Докажите, что если боковые рёбра пирамиды образуют с основанием равные углы, то в основании лежит вписанный многоугольник и вершина пирамиды проектируется в центр описанной около него окружности. |
|
6.В основании треугольной пирамиды лежит прямоугольный треугольник с катетами a и b. Боковые рёбра пирамиды равны l. Найдите высоту пирамиды. |
|
7(в). Докажите, что если у пирамиды равны боковые рёбра и двугранные углы при основании, то эта пирамида является правильной. |
|
8.Три стороны основания четырёхугольной пирамиды равны 5, 7 и 8 (стороны следуют в указанном порядке). Найдите четвёртую сторону основания, если известно, что двугранные углы при основании равны. |
|
9.В пирамиде ABCD площадь грани ABC в четыре раза больше площади грани ABD. Возьмём на ребре CD точку M такую, что CM : MD = 2. Через M проведены плоскости, параллельные граням ABC и ABD. Найдите отношение площадей получившихся при этом сечений. |
|
10.Боковое ребро пирамиды разделено на 100 равных частей, и через точки деления проведены плоскости, параллельные основанию. Найдите отношение площадей наибольшего и наименьшего из получившихся сечений. |
|
11.На боковом ребре AB пирамиды взяты точки K и M так, что AK = BM. Через эти точки проведены сечения, параллельные основанию пирамиды. Известно, что сумма площадей этих сечений составляет |
|
12(т). Все двугранные углы при основании пирамиды равны a, а углы, образуемые боковыми рёбрами с основанием, равны b. Известно, что tg a = k tg b. Сколько сторон имеет основание пирамиды, если k = 2? Чему может быть равно k? |
|
13.Двугранные углы при основании пирамиды равны a, площадь боковой поверхности S. Найдите площадь основания. |
|
14.В основании треугольной пирамиды лежит правильный треугольник. Высота пирамиды равна h. Все боковые грани наклонены к плоскости основания под углом a. Найдите площадь основания. (Рассмотрите все возможности.) |
|
15(в). В основании пирамиды лежит треугольник со сторонами 3, 4 и 5. Боковые грани наклонены к плоскости основания пирамиды под углом 45°. Чему может быть равна высота пирамиды? |
|
16(в). Сторона основания правильной треугольной пирамиды равна a, боковое ребро b. Найдите высоту пирамиды и двугранный угол между боковыми гранями. |
|
17.На гранях правильного тетраэдра с ребром a во внешнюю сторону построены правильные тетраэдры. Докажите, что новые вершины построенных тетраэдров являются вершинами правильного тетраэдра. Найдите его ребро. |
|
18(т). На гранях правильного тетраэдра, как на основаниях, построены равные правильные пирамиды, расположенные вне тетраэдра. Плоские углы в этих пирамидах при вершинах, противолежащих граням тетраэдра, прямые. Рассмотрим многогранник, образованный тетраэдром и указанными пирамидами. Сколько граней у этого многогранника? Как он называется? |
|
19(п). Плоские углы при вершине правильной n-угольной пирамиды равны a. Найдите двугранные углы при основании этой пирамиды. Решите задачу при n = 3; 4. Приведите ответ для произвольного n. |
|
20(в). В основании пирамиды лежит многоугольник, площадь которого равна 6. Плоскость, параллельная основанию, делит высоту пирамиды в отношении 1 : 2 (считая от вершины). Найдите площадь сечения пирамиды этой плоскостью. |
|
21.В основании правильной треугольной пирамиды лежит треугольник площади S, площадь боковой грани равна Q. Найдите площадь сечения этой пирамиды плоскостью, проходящей через сторону основания и середину противоположного рёбра. |
|
22(в). Площадь основания правильной n-угольной пирамиды равна S, а площадь боковой грани равна Q. Найдите двугранные углы при основании этой пирамиды. |
|
23.Имеются две правильные треугольные пирамиды с общим основанием. Все плоские углы при противолежащей вершине одной из пирамид равны 60°, а у другой пирамиды они равны 90°. Найдите отношение высот этих пирамид. |
|
24.В треугольной пирамиде ABCD площади граней ABC и ABD равны 3 и 4. Через точку на ребре CD проведены плоскости, параллельные ABC и ABD и пересекающие пирамиду по равновеликим треугольникам. В каком отношении эта плоскость делит ребро CD ? |
|
25(т). Сколько различных пирамид можно составить из шести отрезков длиной 1, 2, 2, 3, 3, 3 (эти отрезки равны рёбрам пирамиды)? |
|
26(п). Существует ли четырёхугольная пирамида, две противоположные грани которой перпендикулярны плоскости основания? |
|
27(в). Докажите, что в правильной треугольной пирамиде противоположные рёбра попарно перпендикулярны. |
|
28.В пирамиде SABCD с основанием ABCD известны плоские углы при вершине S : ∠ ASB = 30°, ∠ BSC = 40°, ∠ CSD = 50°, ∠ DSA = 80°. В каких пределах могут меняться ∠ ASC и ∠ BSD? |
|
29(п). Все плоские углы при вершине треугольной пирамиды — прямые. Докажите, что эта вершина проектируется в точку пересечения высот противоположной грани. |
|
30.Через середину какого-то ребра правильной треугольной пирамиды проведено сечение, параллельное двум её скрещивающимся рёбрам. Найдите площадь этого сечения, если сторона основания пирамиды равна a, а её боковое ребро равно b. |
|
31(т). Ребро правильного тетраэдра равно a. Чему равно наибольшее значение площади проекции этого тетраэдра на плоскость? |
|
32(т). В пирамиде ABCD грань ABC представляет собой правильный треугольник, ребро DA равно стороне этого треугольника. Все плоские углы при вершине D равны между собой. Чему могут быть равны эти углы? |
|
33(т). В основании пирамиды SABCD лежит четырёхугольник ABCD, в котором AB = BC = 5, AD = DC = AC = 2. Известно также, что SB = 6, а ребро SD является высотой этой пирамиды. Найдите SD. |
|
34(т). Разрежьте пирамиду ABCD на восемь подобных ей и равных между собой пирамид, если: а) AB = CD, ребро AB перпендикулярно CD, а общий перпендикуляр к AB и CD равен половине каждого из них и проходит через середины этих рёбер; б) все плоские углы при вершине D — прямые и DA = DB = DC в) двугранный угол при ребре BC — прямой, ∠ ABC = ∠ BCD = 90° и AB = BC = CD ; г) AC = CB, ∠ ACB = 90°, высота, опущенная из вершины D, проходит через середину AB и равна Существуют ли треугольные пирамиды другого вида, которые можно разрезать на подобные между собой и исходной пирамиде пирамиды (не обязательно на восемь), неизвестно. Эта задача до настоящего момента (времени создания учебника) относится к нерешённым. |

 площади основания пирамиды. Найдите
площади основания пирамиды. Найдите  ;
;
