
Авторы: , Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г..
Издательство:
Просвещение 2015
Тип: Учебник
Подробный решебник (ГДЗ) по Геометрии за 10‐11 (десятый‐одиннадцатый) класс – готовый ответ 10 класс – 279. Авторы учебника: Атанасян, Бутузов, Кадомцев, Киселева, Позняк. Издательство: Просвещение 2015.
Условие /
10 класс / 279
279. Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Решебник №1 / 10 класс / 279

Видеорешение / 10 класс / 279
Решебник №2 / 10 класс / 279


Решебник №3 / 10 класс / 279

Решебник №4 / 10 класс / 279

Оцените решебник:
4.4/5

1476



ГДЗ (готовое домашние задание из решебника) на Номер №279 по учебнику Геометрия. 10-11 классы: учебник для общеобразовательных учреждений : базовый и профильный уровни / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 22-е изд. – Просвещение, 2013-2019г
Условие
Найдите угол между двумя диагоналями граней куба, имеющими общий конец.
Решение 1
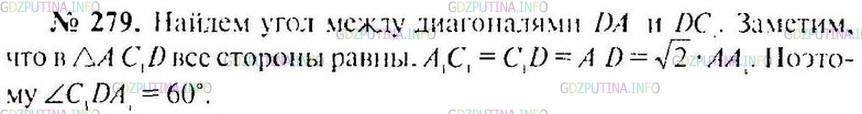
Решение 2
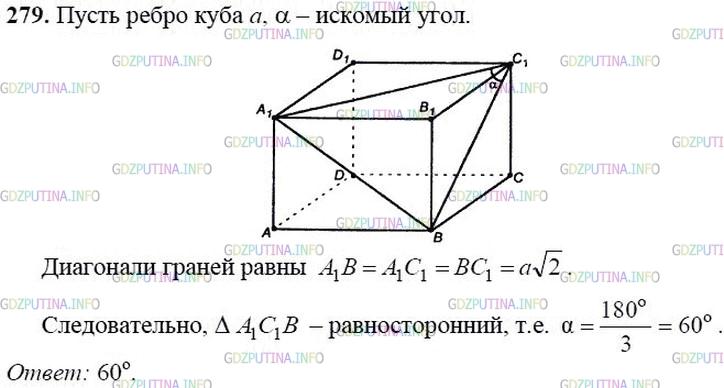
Решение 3
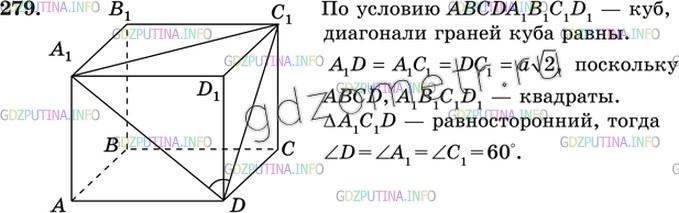
Решение 4
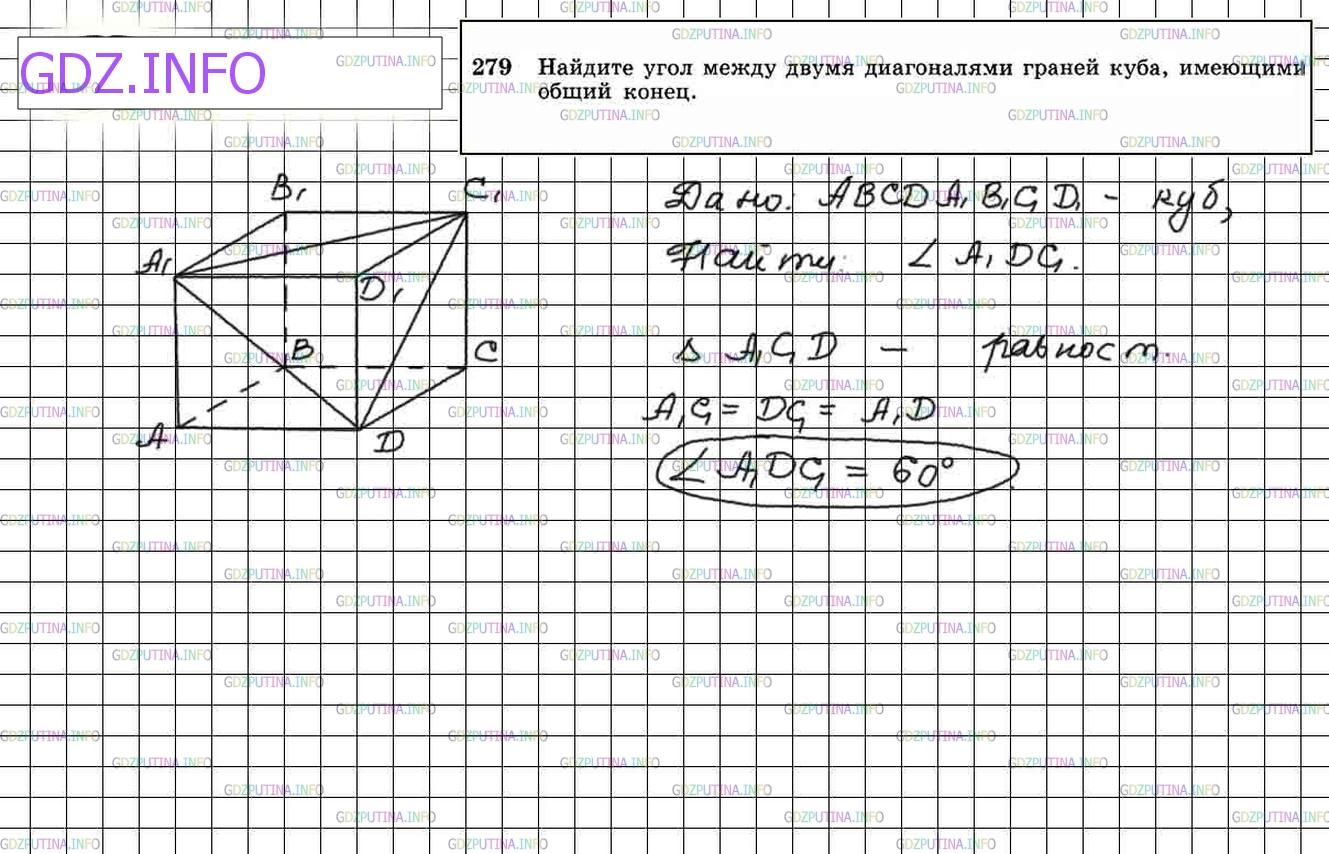
Решение 5

Другие задачи из этого учебника
Популярные решебники
Ваше сообщение отправлено
и скоро будет рассмотрено
Автор:
John Stephens
Дата создания:
27 Январь 2021
Дата обновления:
17 Май 2023

Если бы вы взяли квадрат и нарисовали две диагональные линии, они пересеклись бы в центре и образовали четыре прямоугольных треугольника. Две диагонали пересекаются под углом 90 градусов. Вы можете интуитивно догадаться, что две диагонали куба, каждая из которых проходит от одного угла куба к противоположному углу и пересекается в центре, также пересекаются под прямым углом. Вы бы ошиблись. Определить угол, под которым две диагонали в кубе пересекают друг друга, немного сложнее, чем это может показаться на первый взгляд, но это действительно хорошая практика для понимания принципов геометрии и тригонометрии.
Определите длину ребра как одну единицу. По определению каждое ребро куба имеет одинаковую длину в одну единицу.
Используйте теорему Пифагора, чтобы определить длину диагонали, бегущей от одного угла до противоположного угла на той же грани. Назовите это «короткой диагональю» для ясности. Каждая сторона сформированного прямоугольного треугольника составляет одну единицу, поэтому диагональ должна быть равна √2.
Используйте теорему Пифагора, чтобы определить длину диагонали, бегущей от одного угла до противоположного угла противоположной грани. Назовите это «длинной диагональю». У вас есть прямоугольный треугольник с одной стороной, равной 1 единице, и одной стороной, равной «короткой диагонали», √2 единиц. Квадрат гипотенузы равен сумме квадратов сторон, поэтому гипотенуза должна быть √3. Каждая диагональ, идущая от одного угла куба к противоположному углу, имеет длину √3 единиц.
Нарисуйте прямоугольник, чтобы представить две длинные диагонали, пересекающиеся в центре куба. Вы хотите найти угол их пересечения. Этот прямоугольник будет иметь высоту 1 единицу и ширину √2 единицы. Длинные диагонали делят пополам друг друга в центре этого прямоугольника и образуют два разных типа треугольника. Один из этих треугольников имеет одну сторону, равную одной единице, а две другие стороны равны √3 / 2 (одна половина длины длинной диагонали). Другая также имеет две стороны, равные √3 / 2, но другая ее сторона равна √2. Вам нужно только проанализировать один из треугольников, поэтому возьмите первый и найдите неизвестный угол.
Используйте тригонометрическую формулу c ^ 2 = a ^ 2 + b ^ 2 – 2ab cos C, чтобы найти неизвестный угол этого треугольника. C = 1, а a и b равны √3 / 2. Подставляя эти значения в уравнение, вы определите, что косинус вашего неизвестного угла равен 1/3. Взятие обратного косинуса 1/3 дает угол 70,5 градусов.
btese
Вопрос по геометрии:
Найдите угол между двумя диагоналями граней куба,имеющими общий конец.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
redelund
Найдём угол между диагоналями DA и DC. Заметим, что в ΔAC1D все стороны равны. A1C1=C1D1 = AD = √⋅AA1. Поэтому ∠C1DA1= 60°.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

