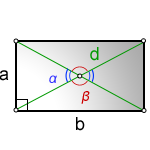
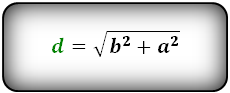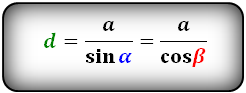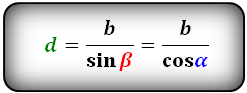Прямоугольник – плоская четырёхугольная геометрическая фигура. Прямоугольник относится к
параллелограммам и обладает некоторыми свойствами:
- Все внутренние углы фигуры прямые.
- Противолежащие стороны попарно параллельны и равны.
- Диагонали прямоугольника (отрезок, соединяющий вершины противоположных внутренних углов) равны.
Точка пересечения делит их на равные отрезки. - Диагональ делит фигуру на 2 одинаковых прямоугольных треугольника.
- Диагональ делит внутренний угол (90°) на 2 угла. Накрест лежащие углы при проведенном отрезке
равны.
- Острый угол между диагоналями прямоугольника через площадь
и диагональ - Угол между диагоналями прямоугольника через угол между
стороной и диагональю - Острый угол между диагоналями прямоугольника через ширину и
диагональ - Острый угол между диагоналями прямоугольника через длину и
диагональ - Острый угол между диагоналями прямоугольника через ширину и
длину - Тупой угол между диагоналями прямоугольника через длину и
диагональ - Тупой угол между диагоналями прямоугольника через ширину и
диагональ - Тупой угол между диагоналями прямоугольника через длину и
ширину
Острый угол между диагоналями прямоугольника через площадь и диагональ
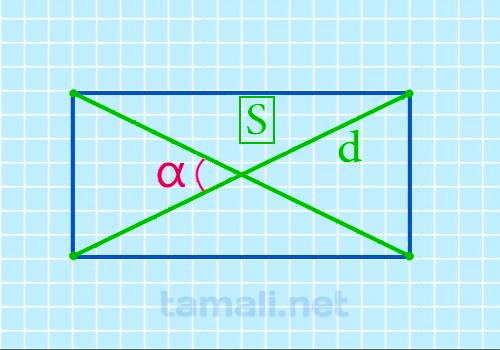
Острый угол (a) между диагоналями, зная площадь (S) и длину диагонали (d) легко можно вычислить по
формуле:
sin a = (2 * S) / d²
где d — диагональ, S — площадь прямоугольника.
Цифр после
запятой:
Результат в:
Через синус находится значение угла. По этой формуле также можно найти тупой угол между диагоналями,
так как 2 данных угла являются смежными, а синусы смежных углов равны.
Пример. Дан прямоугольник, площадь которого равна 108 см², а диагональ – 15 см.
Нужно найти острый угол между диагоналями. Необходимые значения подставляем в формулу sin a = (2 * S) / d² = (2 * 108) / 225 = 0,96. По значению синуса
находится величина острого угла между диагоналями. В данном случае она равна 73,73°.
Угол между диагоналями прямоугольника через угол между стороной и диагональю
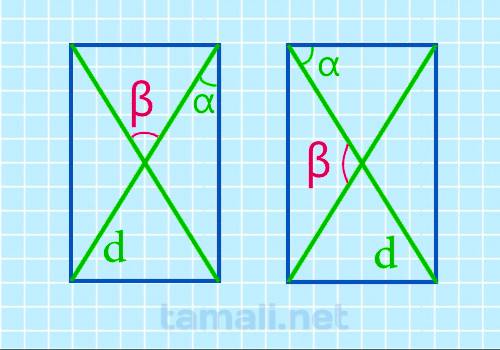
Величина нужного угла (α) в два раза больше угла (β) между стороной и диагональю по свойству углов
равнобедренного треугольника, так как диагонали при пересечении образуют 4 равнобедренных
треугольника. В равнобедренном треугольнике углы при основании (b) равны, а нужный угол является
смежным по отношению к углу при вершине (c), в таком случае c = 180 — α. Сумма углов
треугольника равна 180°. Несложно составить уравнение β+β+180-α=180, которое легко сокращается до
вида
β = 2 * α
где α — угол между стороной и диагональю.
Цифр после
запятой:
Результат в:
Пример. Пусть угол α = 15 (он может быть от 0 до 90º), тогда β = 2 * α = 2 * 15 = 30º
Острый угол между диагоналями прямоугольника через длину и ширину
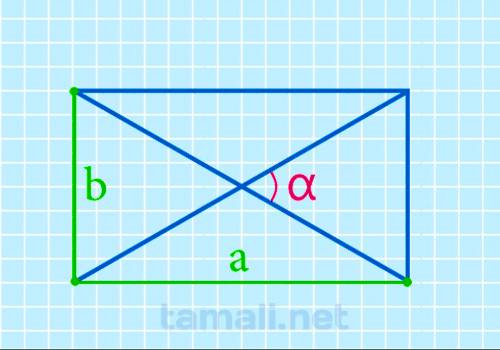
Если в задаче неизвестна длина диагонали, не нужно тратить время на ее поиски. Можно быстро найти
острый угол между диагоналями при помощи длины и ширины прямоугольника по формуле:
α = 2 arctg b / a
где b — ширина прямоугольника, a — длина прямоугольника.
Цифр после
запятой:
Результат в:
Пример. Дан прямоугольник со сторонами 8 см и 6 см. Нужно построить диагонали и
найти острый угол между ними. Угол α = 2 arctg 6 / 8 = 2 arctg 0,75=73,73°.
Острый угол между диагоналями прямоугольника через ширину и диагональ
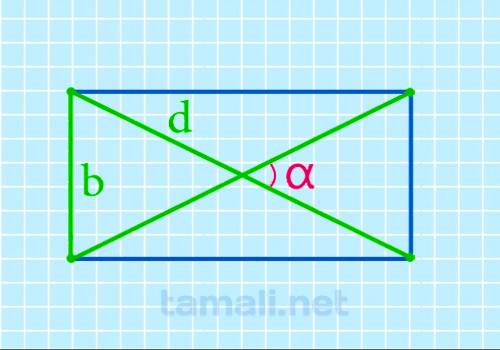
Значение нужного угла можно определить, зная длину диагонали и ширины (B) четырёхугольника, по
формуле:
α = 2 arcsin b / d
где b — ширина прямоугольника, d — диагональ.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим применение формулы в конкретной задаче. Дан прямоугольник, ширина
которого равна 3 мм, а длина диагонали – 5 мм. Необходимо найти острый угол между
диагоналями. Применив данную формулу, находим значение нужного угла: a = 2 * arcsin 0,6 = 73,73°.
Острый угол между диагоналями прямоугольника через длину и диагональ
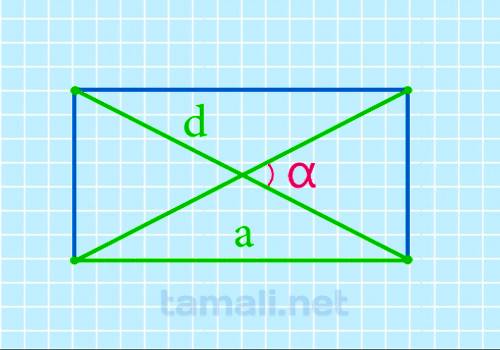
Если неизвестна ширина прямоугольника, но есть значение длины (a), можно также просто найти острый
угол между диагоналями. Формула почти идентична предыдущей:
α = 2 arccos a / d
где a — длина прямоугольника, d — диагональ.
Цифр после
запятой:
Результат в:
Пример. В прямоугольнике с длиной 8 см, в котором проведены диагонали длиной 10 см,
найти острый угол между диагоналями. Угол α = 2arccos 8 / 10 = 2arccos 0,8 = 73,73°.
Тупой угол между диагоналями прямоугольника через ширину и диагональ
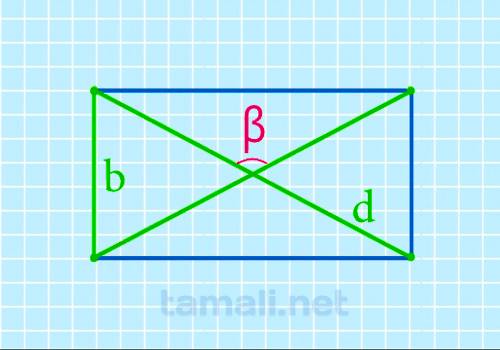
Для того чтобы быстро вычислить значение данного угла при помощи известной ширины и диагонали
прямоугольника, нужно воспользоваться следующей формулой:
β = 2 arccos b / d
где b — ширина прямоугольника, d — диагональ.
Цифр после
запятой:
Результат в:
Пример. Известна ширина прямоугольника, она равна 8 мм. А длина диагонали равна 17
мм. Задача найти значение тупого угла между диагоналями.
Вставив данные в формулу, вы получите
правильный результат. Таким образом, β = 2 arccos 8 / 17 = 2 arccos 0,47 = 123,85°.
Тупой угол между диагоналями прямоугольника через длину и диагональ
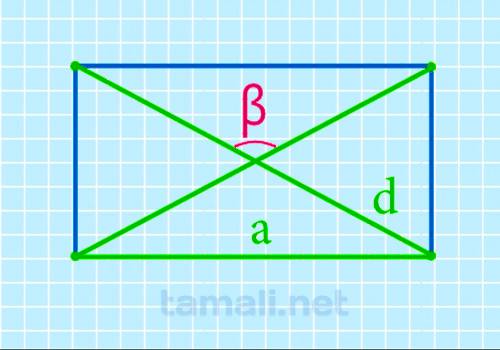
Можно, конечно, применить предыдущую формулу и найти острый угол через длину и диагональ, а потом
вычесть значение из 180°. Но есть упрощенная формула для быстрой скорости решения: тупой угол между
диагоналями
β = 2 arcsin a / d
где a — длина прямоугольника, d — диагональ.
Цифр после
запятой:
Результат в:
Пример. Дан прямоугольник с длиной равной 20 см, в котором проведены диагонали
длиной 25 см. Чтобы найти нужную величину, подставляем значения в формулу: β = 2 arcsin 20 / 25 = 2 arcsin 0,8 = 106°.
Тупой угол между диагоналями прямоугольника через длину и ширину
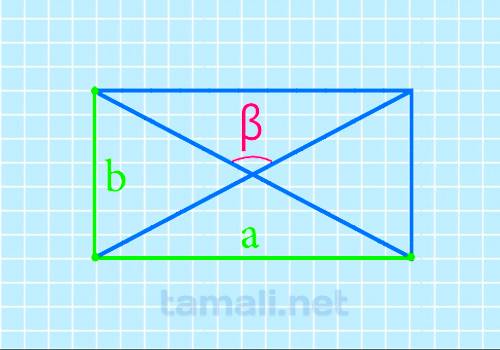
Формула для определения тупого угла между диагоналями прямоугольника через известные значения длины и
ширины такова:
β = 2 arctg a / b
где a — длина прямоугольника, b — ширина прямоугольника.
Цифр после
запятой:
Результат в:
Пример. Дан прямоугольник со сторонами 15 см и 8 см. Вычислим значение тупого угла,
подставив данные в формулу: β = 2arctg 15 / 8 = 2 arctg 0,5= 123,85°.
Стоит отметить, что при использовании указанных в статье правил нужно владеть знаниями о
тригонометрических функциях. Для того чтобы быстро определять углы, образованные пересечением
диагоналей прямоугольника, поможет именно данный список формул, которые необходимо знать наизусть.
Если на решение задач по геометрии дается небольшой промежуток времени, к примеру, контрольная или
экзамен, лучше отложить сложные алгоритмы и воспользоваться упрощенными формулами.
Параллелограмм относится к выпуклым четырехугольным геометрическим фигурам. Его основные
отличительные признаки от других фигур: равные и попарно параллельные противоположные стороны,
равные противолежащие углы. Диагонали фигуры всегда делятся точкой пересечения на равные отрезки, а
также они делят параллелограмм на 2 одинаковых треугольника. Еще одним главным свойством
четырёхугольника является то, что сумма квадратов диагоналей равна двум суммам квадратов смежных
сторон параллелограмма.
Биссектрисы внутренних углов данного четырёхугольника всегда отсекают от него равнобедренный
треугольник, а также они равны между собой. Сумма углов параллелограмма равна 360°, как и у других
четырёхугольников.
К параллелограммам относятся: квадрат (четырёхугольник с равными сторонами и
равными прямыми внутренними углами), прямоугольники и ромбы (параллелограмм с равными сторонами).
Эти фигуры часто встречаются в школьной программе на уроках геометрии.
Для чего необходимо вычисление угла между диагоналями параллелограмма
- Для нахождения сторон четырёхугольника (длины и ширины).
- Для нахождения площади и периметра фигуры.
- Для нахождения углов между стороной и диагональю.
- Для нахождения длины диагонали.
Знание свойств геометрических фигур помогает справиться с задачей любой сложности. Постоянная
практика с использованием формул способствует быстрому запоминанию информации, помогает проработать
маршруты и теоремы, которые западают.
Прямоугольник часто встречается в решении задач по геометрии. Важно знать все его свойства и уметь
пользоваться правилами и теоремами для успешного нахождения результата. Упрощенные формулы и
несколько конкретных примеров помогут определить правильный алгоритм решения и быстро найти
ответ.
Прямоугольник. Формулы и свойства прямоугольника
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 – b2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
|
Угол между диагоналями прямоугольника можно определить по формуле 2*arctg(a/b), где а и b – стороны прямоугольника. Формула справедлива для любого прямоугольника, но ни в коем случае не применима для параллелограммов. система выбрала этот ответ лучшим MrClous 9 лет назад Диагональ многоугольника – отрезок, который соединяет две не граничащие между собой вершины фигуры (т.е. несмежные вершины или не принадлежащие одной стороне многоугольника). В параллелограмме, зная длину диагоналей и длину сторон, можно рассчитать углы между диагоналями. Юрий Восковец 9 лет назад Зная углы между диагоналями и одной из сторон (это через тригонометрические функции, зная размеры прямоугольника) и то, что сумма углов треугольника равна 180 градусов – вполне можно найти желаемый угол между диагоналями. Знаете ответ? |
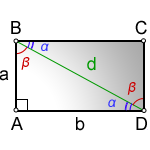
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
d – диагональ прямоугольника
a, b – стороны
α, β – углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
Формулы диагонали через сторону и угол, (d):
Формулы величины углов через диагональ и стороны, (α, β):
2. Формулы углов между диагоналями в прямоугольнике.
d – диагонали прямоугольника
a, b – стороны
α, β – углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):
- Подробности
-
Опубликовано: 27 октября 2011
-
Обновлено: 13 августа 2021
Зная угол между диагоналями, можем найти оба угла пересечения диагонали со стороной. Если построить перпендикуляр из точки пересечения диагоналей в сторону – полуось симметрии прямоугольника, то мы получим прямоугольный треугольник, подобный тому, который образует диагональ со сторонами. Из этого треугольника видно, что углы, образованные сторонами и диагональю, в два раза меньше, чем углы при пересечении диагоналей. (рис. 56.2, 56.3)
α=γ/2
β=δ/2
При этом можно использовать свойство вертикальных углов, которое говорит о том, что острый и тупой угол в сумме дают 180 градусов, для того чтобы найти второй центральный угол.
m(
Или из прямоугольного треугольника с диагональю и сторонами найти сначала угол α и затем вычесть его из 90 градусов.
m(
Теперь имея угол, между стороной и диагональю, и саму диагональ, можно найти стороны, используя прямоугольный треугольник. (рис. 56.1) Отношение противолежащего катета – стороны к гипотенузе – диагонали является синусом угла α, следовательно, сторона прямоугольника равна произведению синуса на диагональ. Вторая сторона будет равна тогда произведению косинуса угла α на диагональ, так как она является прилежащей углу.
b=d sin(α/2)
a=d cos(α/2)
Те же самые формулы в обратном порядке можно использовать для угла β:
a=d sinβ
b=d cosβ
Если необходимо найти периметр и площадь прямоугольника, следует подставить в формулы вместо сторон выведенные выражения.
P=2(a+b)=2(d sinβ+ d cosβ )=2d(sinβ+ cosβ)
P=2d(sinα+ cosα)
S=ab=d sinβ* d cosβ=d^2 sinβ cosβ
S=d^2 sinα cosα
Для того чтобы найти радиус окружности, которую можно описать вокруг прямоугольника, нужно разделить его диагональ на два, так как она совпадает с диаметром. (рис.56.3)
R=d/2