Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны. Частными
случаями параллелограмма являются прямоугольник и ромб. Квадрат одновременно является частным
случаем и прямоугольника и ромба, поэтому все выявленные для параллелограмма зависимости справедливы
для прямоугольника, квадрата и ромба.
На практике необходимость определения угла между диагоналями на основе прочих элементов может
возникнуть, в частности, при необходимости производства построений на местности и для перепроверки
уже проведенных построений.
- Острый угол между диагоналями параллелограмма через площадь
и диагонали - Угол между диагоналями параллелограмма через диагонали и
сторону - Угол между диагоналями параллелограмма через две стороны и
диагонали
Через площадь и диагонали
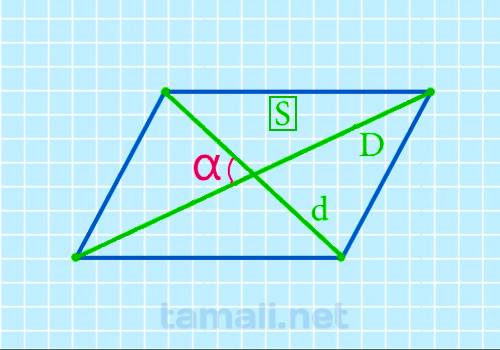
Для нахождения острого угла между диагоналями параллелограмма следует воспользоваться формулой:
sin α = 2S/(Dd)
где α – острый угол между диагоналями, S – площадь параллелограмма, D и d – его диагонали.
Цифр после
запятой:
Результат в:
Приведем пример расчета по формуле для наглядного случая, когда диагонали перпендикулярны, и площадь
данного ромба равняется половине площади прямоугольника, в который данный ромб можно вписать.
При D = 20 мм, d = 10 мм, площадь описанного прямоугольника равна 20*10=200 мм², откуда S = 200/2=100 мм².
Вычисления дают sin α = 2S/(Dd) = 2*100/(20*10) = 1, откуда α = 90°. Известный факт – диагонали
ромба перпендикулярны.
Через две стороны и диагонали
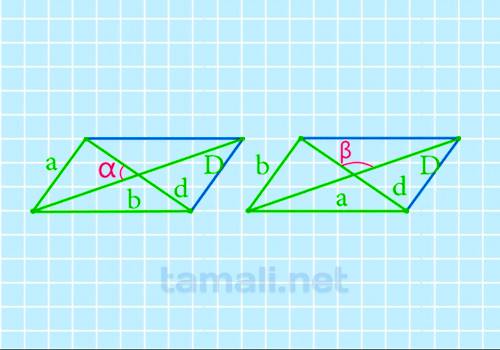
В предыдущей формуле угол определялся через диагонали и одну сторону, в данной задаче требуется
определить угол по диагоналям и 2 сторонам. Тем самым, одно из условий является избыточным, и фигура
по произвольным данным может не оказаться параллелограммом. Но для случая параллелограмма, т.е.
взаимной увязки данных, формулы таковы:
cos α = (b2-a2)/(Dd), cos β = (a2-b2)/(Dd)
где a и b – стороны параллелограмма, α и β – углы между диагоналями (взаимно дополнительные до
180°).
Цифр после
запятой:
Результат в:
Пример приведем по предыдущему случаю, остается только рассчитать недостающую сторону b, которая из
простых соображений (воспользовавшись правилом длины катета против угла в 30°) оказывается равной 20
мм. Вычисляем: cos α = (b²-a²)/(Dd) = (20²-34,64²)/(40*40) = -0,5, откуда
α = 120°.
Через диагонали и сторону
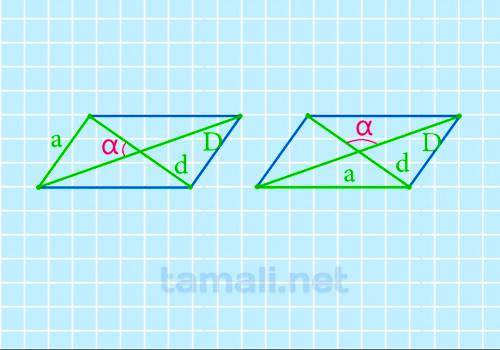
Для нахождения угла между диагоналями параллелограмма через диагонали и сторону формула такова:
cos α = (D² + d² – 4a²)/(2Dd)
где a – сторона параллелограмма, остальные обозначения прежние.
Цифр после
запятой:
Результат в:
Здесь следует считаться с тем, что если в предыдущей задаче угол по условию являлся острым, в данной
задаче он может быть и тупым, с отрицательным значением косинуса угла.
Пример расчета опять-таки по наглядному случаю, когда обе диагонали равны. Это прямоугольник с
диагоналями D = 40 мм и d = 40 мм. При угле между диагоналями 120° половина диагонали составит 40/2 = 20 мм, половина высоты прямоугольника (она же – половина короткой
стороны) составит половину от половины диагонали (в прямоугольном треугольнике противолежащий углу в
30° катет равен половине гипотенузы), т.е. 10 мм, откуда половина стороны параллелограмма составит
√(20²-10²)=√300=17,32 мм, а сторона параллелограмма a = 2*17,32=34,64 мм.
Подставляем в формулу: cos α = (D² + d² – 4a²)/(2Dd) = (40²+40²-4*34,642) = ‑1600/(2*40*40) = -0,5.
Значению косинуса -0,5 соответствует угол 120°. Это же значение даст и калькулятор.
Квадрат достаточно задать одним элементом – стороной. Для задания прямоугольника необходимо задать
уже две его смежные стороны; для ромба сторону и угол между сторонами. Для задания же
параллелограмма необходимо задание 3 его взаимно независимых элементов. Это могут быть 2 смежные
стороны и угол между ними, но возможно и иное задание.
В любом четырехугольнике можно провести 2 диагонали, и они также могут входить в набор элементов для
задания фигуры. В данной статье приводятся справочные формулы для определения угла между диагоналями
параллелограмма через другие его элементы. Рассчитать же этот угол для каждого из 3 рассматриваемых
случаев позволят калькуляторы сайта, в которые необходимо ввести известные элементы, и в результате
получить синус или косинус искомого угла либо сам угол в градусах или радианах.
Как найти угол между диагоналями параллелограмма
Прежде чем искать решение поставленной задачи, следует выбрать наиболее подходящий метод ее решения. Геометрический метод требует тдополнительных построений и их обоснования, поэтому в данном случае наиболее удобным представляется использование векторной методики. Для этого используются направленные отрезки – векторы.

Вам понадобится
- – бумага;
- – ручка;
- – линейка.
Инструкция
Пусть параллелограмм задан векторами двух его сторон (остальные две попарно равны) в соответствии с рис. 1. Вообще-то равных векторов на плоскости сколь угодно много. Для этого требуется равенство их длин (точнее модулей – |a|) и направления, которое задается наклоном к какой-либо оси (в декартовых координатах это ось 0Х). Поэтому для удобства в задачах подобного типа векторы, как правило, задают их радиус-векторами r=а, у которых начало всегда лежит в начале координат.
Для нахождения угла между сторонами параллелограмма понадобится вычислить геометрическую сумму и разность векторов, а также их скалярное произведение (a,b). По правилу параллелограмма геометрическая сумма векторов a и b равна некоторому вектору с=а+b, который построен и лежит на диагонали параллелограмма AD. Разность a и b – вектор d=b-a, построенный на второй диагонали BD. Если векторы заданы координатами, а угол между ними составляет ф, тогда их скалярное произведение – это число, равное произведению модулей векторов и cosф (см. рис1): (a, b) = |a||b|cos ф
В декартовых координатах если а={x1, y1} и b={x2, y2}, то (a, b) = x1y2 +x2y1. При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 +x2^2. Для вектора b – аналогично. Тогда: |a||b|cos ф = x1y2 +x2y1. Следовательно cosф=(x1y2 +x2y1)/(|a||b|). Таким образом алгоритм решения задачи состоит в следующем:1. Нахождение координат векторов диагоналей параллелограмма как векторов суммы и разности векторов его сторон с=а+b и d=b-a. При этом соответствующие координаты a и b просто складываются или вычитаются. c= a+ b ={x3, y3}= { x1+x2, y1+y2},d= b-a ={x4, y4}={ x2 –x1, y2-y1}. 2. Нахождение косинуса угла между векторами диагоналей (назовем его фД) по приведенному общему правилу cosфд=(x3y3 +x4y4)/(|c||d|)
Пример. Найти угол между диагоналями параллелограмма, заданного векторами своих сторон a={1, 1} и b ={1, 4}. Решение. Согласно приведенному алгоритму вам необходимо найти векторы диагоналей c={1+1, 1+4}={2, 5} и d={1-1, 4-1}={0, 3}. Теперь вычислите cosфд =(0+15)/(sqrt(4+25)sqrt9)= 15/3sqrt29=0,92. Ответ: фд= arcos(0,92).
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
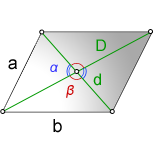
a, b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
β – тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
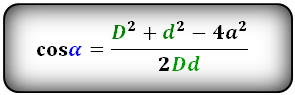
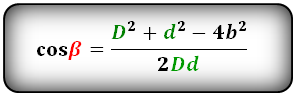
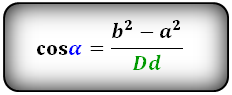
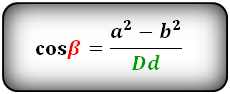
Формула синуса острого и тупого углов через площадь (S) и диагонали:
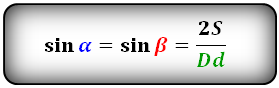
Формулы соотношения острого и тупого углов между диагоналями:

Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
- Подробности
-
Опубликовано: 06 ноября 2011
-
Обновлено: 13 августа 2021
Найти угол между диагоналями параллелограмма
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β

a , b – стороны параллелограмма
D – большая диагональ
d – меньшая диагональ
α – острый угол между диагоналями
β – тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
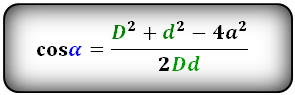
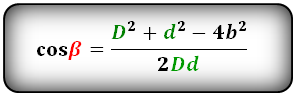
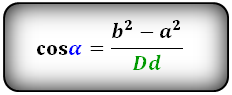
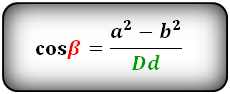
Формула синуса острого и тупого углов через площадь (S) и диагонали:
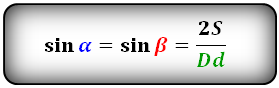
Формулы соотношения острого и тупого углов между диагоналями:

Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Найдите угол между диагоналями параллелограмма, если заданы три его вершины A(2 ; 1 ; 3) , B(5 ; 2 ; −1) , C(−3 ; 3 ; −3) ?
Математика | 10 – 11 классы
Найдите угол между диагоналями параллелограмма, если заданы три его вершины A(2 ; 1 ; 3) , B(5 ; 2 ; −1) , C(−3 ; 3 ; −3) .
Через векторы решается как то.

Даны точки А(2 ; 1 ; 3) В(5 ; 2 ; – 1) С( – 3 ; 3 ; – 3)
Сторонами параллелограмма будут АВ, ВС, СD, DA
Найдем диагональ АС :
Координаты точки D(x ; y ; z)
Надо найти диагональ BD
Диагонали пересекаются и точкой пересечения делятся пополам :
пусть точкой пересечения будет точка О, тогда координаты точки О (на диагонали АС :
с другой стороны координатами точки O (на диагонали BD)будут :
приравняем и найдем координаты точки D
таким образом D( – 6 ; 3 ; 1)
теперь найдем BD
найдем длину |AC| и|BD|

Найдите угол между диагоналями параллелограмма построенного на векторах a = 2i + j и b = – j + 2k?
Найдите угол между диагоналями параллелограмма построенного на векторах a = 2i + j и b = – j + 2k.

Вычислите угол между диагоналями параллелограмма с вершинами : А(2, 1) В(7, 2) С(9, 3) Д(4, 2)?
Вычислите угол между диагоналями параллелограмма с вершинами : А(2, 1) В(7, 2) С(9, 3) Д(4, 2).

Постройте параллелограмм если дана точка пересечения его диагоналей и места расположения двух соседских вершин?
Постройте параллелограмм если дана точка пересечения его диагоналей и места расположения двух соседских вершин.

В параллелограмме ABCD проведена диагональ AC?
В параллелограмме ABCD проведена диагональ AC.
Угол ACB равен 65 градусов, а угол CAB равен 17 градусов.
Найдите угол А параллелограмма ABCD.

Даны три последовательные вершины параллелограмма A( – 5, 5) B(1, 3) C(3, 7)Найтиуравнение стороны ADуравнение диагонали BDугол между диагоналями параллелограмма?
Даны три последовательные вершины параллелограмма A( – 5, 5) B(1, 3) C(3, 7)
уравнение стороны AD
уравнение диагонали BD
угол между диагоналями параллелограмма.

Найдите сумму длин диагоналей параллелограмма построенного на векторах a(3, 1)и b(1, 3)?
Найдите сумму длин диагоналей параллелограмма построенного на векторах a(3, 1)и b(1, 3).

В параллелограмме VHKL диагонали LH в два раза больше стороны HK и угол VLH = 114?
В параллелограмме VHKL диагонали LH в два раза больше стороны HK и угол VLH = 114.
Найдите угол между диагоналями параллелограмма.

Диагональ параллелограмма образует со сторонами углы в 20 и 50?
Диагональ параллелограмма образует со сторонами углы в 20 и 50.
Найти больший угол параллелограмма.

В параллелограмме диагональ BD перпендикулярна стороне AB ?
В параллелограмме диагональ BD перпендикулярна стороне AB .
Найдите периметр параллелограмма если диагональ BD равна 3√3 а угол BAD равен 30°.

В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и угол ACD равен 104 градуса Найдите угол между диагоналями параллелограмма Ответ дайте в градусах?
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и угол ACD равен 104 градуса Найдите угол между диагоналями параллелограмма Ответ дайте в градусах.
Вы зашли на страницу вопроса Найдите угол между диагоналями параллелограмма, если заданы три его вершины A(2 ; 1 ; 3) , B(5 ; 2 ; −1) , C(−3 ; 3 ; −3) ?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 – 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Lg100 = 2 lg10 = 1 3x – 11 = 100 3x = 111 x = 37 37 – 27 = 10 2 + 1 = 3.

1)78дм 2) 89мм 3) 8см 3мм 4) 5дм 6см 5)1м 2дм 6)4дм 7см 7)33см.

, т. к 5% это 0, 05 то : 15000÷1, 05 = 14286 сумма должна пролежать второй год. Т. к. Процент сложный, то : 14286÷1, 05 = 13606 сумма которую необходимо положить на 2 года под 5%. Ответ : 13606 Проверка : 13606 под 5% = 14286 за 1 год 14286 под 5%..
Формулы параллелограмма
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
Признаки и свойства параллелограмма
- Противоположные стороны параллельны и равны.
- Противоположные углы равны
- Точка пересечения диагоналей делит их пополам.
- Сумма углов четырехугольника прилегающих к любой стороне равна 180°
- В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
- Сумма углов параллелограмма равна 360°
- Каждая диагональ делит параллелограмма на два равных треугольника
- Биссектрисы противоположных углов параллелограмма всегда параллельны
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Формулы стороны параллелограмма
Длины сторон через диагонали и угол между ними
Длина стороны через диагонали и известную сторону
Длины сторон через высоты и угол между сторонами
Формулы диагоналей параллелограмма
Длина диагонали через стороны и углы между ними
Длина диагонали через стороны и известную диагональ
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями
Формулы углов параллелограмма
Косинус острого угла
Косинус тупого угла
Синус острого и тупого угла через площадь и стороны параллелограмма
Формулы углов между диагоналями параллелограмма
Косинус острого угла через стороны и диагонали
Косинус тупого угла через стороны и диагонали
Синус острого и тупого угла через площадь и диагонали
[spoiler title=”источники:”]
http://matematika.my-dict.ru/q/2075274_najdite-ugol-mezdu-diagonalami-parallelogramma-esli/
http://calc-online24.ru/formula/parallelogram
[/spoiler]
Для расчёта всех основных параметров параллелограмма воспользуйтесь калькулятором.
Признаки и свойства параллелограмма
- Противоположные стороны параллельны и равны.
- Противоположные углы равны
- Точка пересечения диагоналей делит их пополам.
- Сумма углов четырехугольника прилегающих к любой стороне равна 180°
- В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон
- Сумма углов параллелограмма равна 360°
- Каждая диагональ делит параллелограмма на два равных треугольника
- Биссектрисы противоположных углов параллелограмма всегда параллельны
- Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Формулы стороны параллелограмма
Длины сторон через диагонали и угол между ними
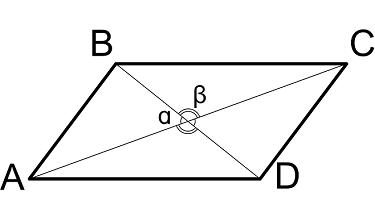
$$
AB = {1 over 2} * sqrt{AC^2 + BD^2 – 2 * AC * BD * cos(α)}
$$
$$
AB = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(β)}
$$
$$
BC = {1 over 2} * sqrt{AC^2 + BD^2 – 2 * AC * BD * cos(β)}
$$
$$
BC = {1 over 2} * sqrt{AC^2 + BD^2 + 2 * AC * BD * cos(α)}
$$
Длина стороны через диагонали и известную сторону
$$
AB = sqrt{AC^2 + BD^2 – 2 * BC^2 over 2}
$$
$$
BC = sqrt{AC^2 + BD^2 – 2 * AB^2 over 2}
$$
Длины сторон через высоты и угол между сторонами
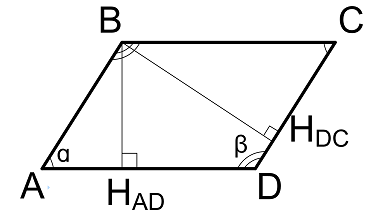
$$
AB = {BH_{AD} over sin(α)} = {BH_{AD} over sin(β)}
$$
$$
BC = {BH_{DC} over sin(α)} = {BH_{DC} over sin(β)}
$$
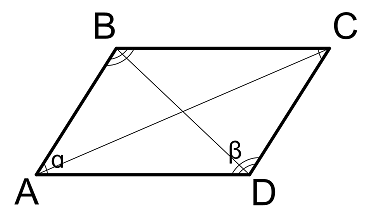
Формулы диагоналей параллелограмма
Длина диагонали через стороны и углы между ними
$$
AC = sqrt{AB^2 + BC^2 – 2 * AB * BC * cos(β)}
$$
$$
AC = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(α)}
$$
$$
BD = sqrt{AB^2 + BC^2 + 2 * AB * BC * cos(β)}
$$
$$
BD = sqrt{AB^2 + BC^2 – 2 * AB * BC * cos(α)}
$$
Длина диагонали через стороны и известную диагональ
$$
AC = sqrt{2 * AB^2 + 2 * BC^2 – BD^2}
$$
$$
BD = sqrt{2 * AB^2 + 2 * BC^2 – AC^2}
$$
Длина диагонали через площадь параллелограмма, известную диагональ и угол между диагоналями

$$
AC = {2 * S over BD * sin(α)} = {2 * S over BD * sin(β)}
$$
$$
BD = {2 * S over AC * sin(α)} = {2 * S over AC * sin(β)}
$$
Формулы углов параллелограмма

Косинус острого угла
$$
cos(α) = {AB^2 + BC^2 – BD^2 over 2 * AB * BC}
$$
Косинус тупого угла
$$
cos(β) = {AB^2 + BC^2 – AC^2 over 2 * AB * BC}
$$
Синус острого и тупого угла через площадь и стороны параллелограмма
$$
sin(α) = sin(β) = {S over AB * BC}
$$
Формулы углов между диагоналями параллелограмма

Косинус острого угла через стороны и диагонали
$$
cos(α) = {AC^2 + BD^2 – 4 * AB^2 over 2 * AC * BD}
$$
$$
cos(α) = {BC^2 – AB^2 over AC * BD}
$$
Косинус тупого угла через стороны и диагонали
$$
cos(β) = {AC^2 + BD^2 – 4 * BC^2 over 2 * AC * BD}
$$
$$
cos(β) = {AB^2 – BC^2 over AC * BD}
$$
Синус острого и тупого угла через площадь и диагонали
$$
sin(α) = sin(β) = {2 * S over AC * BD}
$$
Формула высоты параллелограмма

$$
BH_{AD} = AB * sin(α) = AB * sin(β)
$$
$$
BH_{DC} = BC * sin(α) = BC * sin(β)
$$
Формула биссектрисы параллелограмма
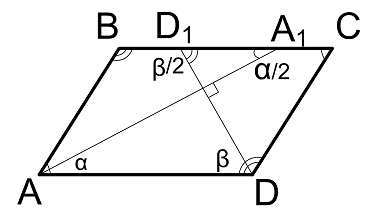
$$
AA_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 – 2 * cos(β)}
$$
$$
AA_1 = 2 * AB * cos({α over 2})
$$
$$
DD_1 = 2 * AB * sin({β over 2}) = AB * sqrt{2 – 2 * cos(β)}
$$
$$
DD_1 = 2 * AB * cos({α over 2})
$$
