Здравствуйте, уважаемые читатели. В этой статье рассмотрим задачу из задания №23 ОГЭ по математике. Это геометрическая задача на вычисление. Бояться второй части ОГЭ не надо. Задание №23 оно почти такое же по простоте, как и задачи из первой части ОГЭ Единственное требование – это написать решение задачи, а не угадать ответ. Давайте начнем.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба
Построим рисунок и запишем дано
Решение
1) Так как диагонали в параллелограмме точкой пересечения делятся пополам, то
2) Рассмотрим треугольник АОК – прямоугольный. АО=30, ОК = 15 (по условию), значит по свойству прямоугольного треугольника (если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30 градусов). Получаем, что:
3) Диагонали в ромбе делят углы пополам, значит:
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог
Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, “сплющите” его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 – 2 * x^2 * cos(a), из него следует a = arccos((2x^2 – d^2)/2x^2). (Я говорю “найти угол”, а не “найти углы”, потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
Учебник
Геометрия, 11 класс
Ромб: Свойства, Формулы. Задачи
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
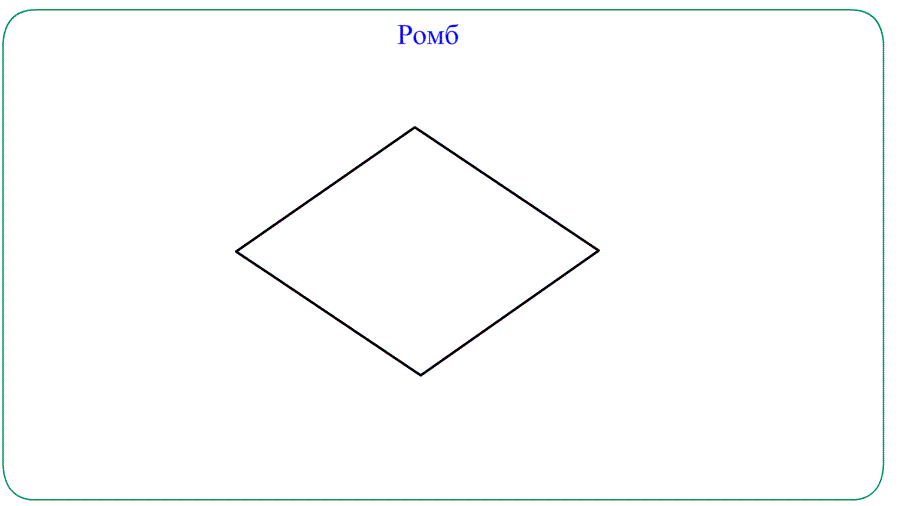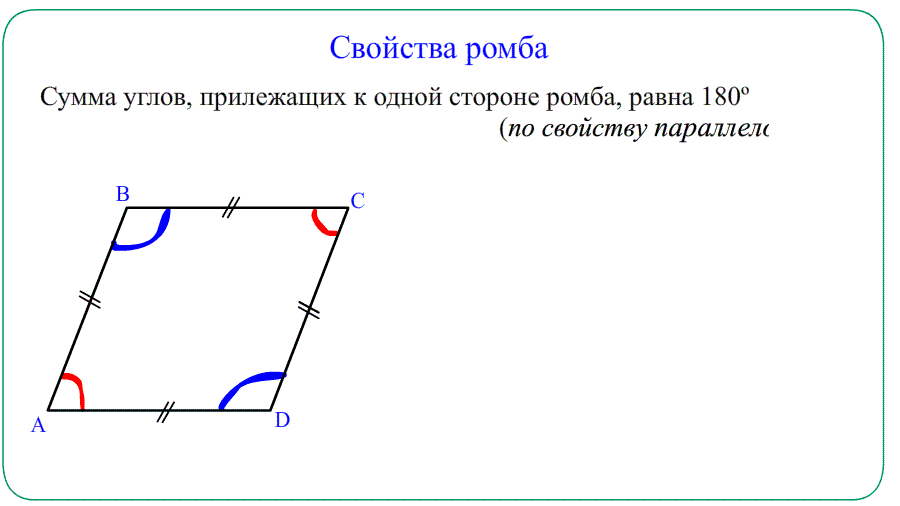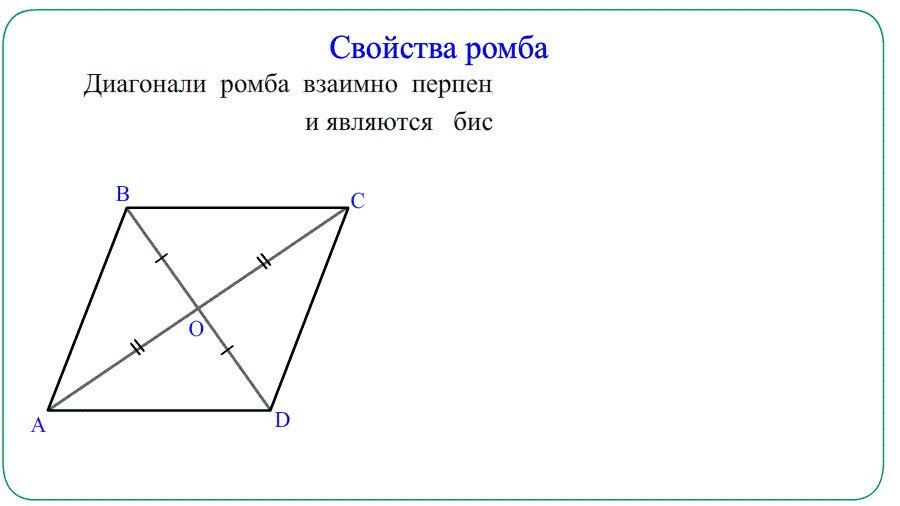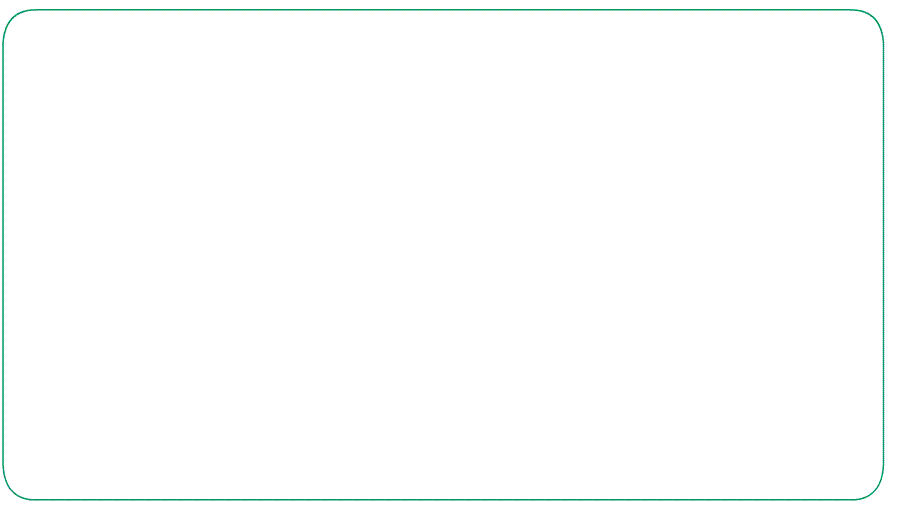
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая – $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . – половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ – пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
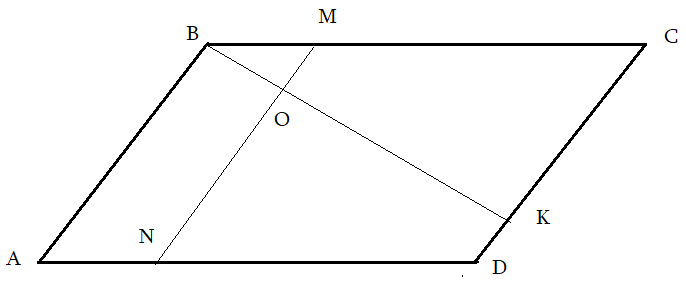
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ – параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ – квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто стоящее – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая – $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . – половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали – суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ – пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ – параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ – квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб – это параллелограмм, у которого все стороны равны.
- “Чтоб Выучить, распознать нечто неподвижное – узнать его в движении, при изменениях”
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей – ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали – новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали – ромб совпадает с самим собой. Симметрия.
Замечание: Если “зряче видим” центральную и осевые симметрии ромба, то все его свойства у нас “в кармане”.
Свойства ромба:
- Ромб симметричен относительно точки O – пересечения диагоналей. O – центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ – ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов – делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.


Квадрат – одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: “Односторонние углы”: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: “В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник – стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Углы ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).

Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac<large h> <large a>) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac<large h><large sin alpha>=frac<large a><large sin 90°>.) | (3) |
| (small sin alpha=frac<large h><large a>) | (4) |
| (small alpha=mathrmfrac<large h><large a>) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).

Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac<large h^2><large S>, ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac<large h><large a>=mathrmfrac<large h><large frac |
(9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).

Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac<large S><large a^2>. ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.

| (small h=frac<large d_1d_2><large sqrt>.) | (11) |
| (small a=frac<large sqrt><large 2>.) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac<large h><large a>) ( small =frac<frac<large d_1d_2><large sqrt>><frac<large sqrt><large 2>> ) ( small =frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (13) |
| (small alpha=mathrm frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).

Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac<alpha> <2>.) Тогда для треугольника AOB имеют места следующие равненства:
(small frac<large AO><large a>=sin frac<alpha><2>,)
(small frac<large AO><large a>=cos frac<beta><2>)
| (small sin frac<alpha><2>=frac<large d><large 2a>) | (15) |
| (small cos frac<beta><2>=frac<large d><large 2a >.) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac<alpha><2>=±sqrt<frac<large 1-cos alpha><large 2 >>,) | (17) |
| (small cosfrac<beta><2>=±sqrt<frac<large 1+cos beta><large 2 >>.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac<alpha><2>,) | (19) |
| (small cos beta=2cdot sin^2 frac<beta><2>-1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac<large d^2><large 2a^2>,) | (21) |
| (small cos beta=frac<large d^2><large 2a^2>-1.) | (22) |
| (small alpha=mathrm left(1- frac<large d^2> <large 2a^2>right),) | (23) |
| (small beta=mathrm left( frac<large d^2><large 2a^2>-1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.

В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac<large 2 cdot r><large a>) | (26) |
| (small alpha=mathrmfrac<large 2 cdot r><large a>) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
Геометрические фигуры. Ромб. Углы ромба. Как найти угол ромба.
Углы ромба, нахождение:
1. Сумма 4-х внутренних углов ромба равняется 360°, точно так же как и у всякого четырехугольника. Противоположные углы ромба имеют одинаковую величину, причем, всегда в 1-ой паре равных углов — углы острые, во второй – тупые. 2 угла, которые прилегают к 1-ной стороне в сумме составляют развернутый угол.
Ромбы с равным размером стороны могут внешне довольно сильно отличаться друг от друга. Это разница объясняется различной величиной внутренних углов. То есть, для определения угла ромба не хватит знать лишь длину его стороны.
2. Для вычисления величины углов ромба хватит знать длины диагоналей ромба. После построения диагоналей ромб разбивается на 4 треугольника. Диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.
Ромб — симметричная фигура, его диагонали есть в одно время и осями симметрии, вот почему каждый внутренний треугольник равен остальным. Острые углы треугольников, которые образованы диагоналями ромба, равняются ½ искомых углов ромба.
3. Тангенс острого угла прямоугольного треугольника соответствует отношению противолежащего катета к прилежащему. ½ любой из диагоналей ромба оказывается катетом прямоугольного треугольника.
Обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — А (острый) и В (тупой), теперь из соотношения сторон в прямоугольных треугольниках внутри ромба находим:
4. Из формулы двойного угла tg (2α) = 2/(сtg α – tg α) находим тангенсы углов ромба:
По тригонометрическим таблицам находят углы, которые соответствуют полученным значениям тангенсов.
Острый угол ромба равен 60 градусам.
Когда острый угол ромба = 60°, значит, диагональ равняется стороне ромба и делит его на 2 одинаковых равносторонних треугольника.

∆ ABD и ∆ BCD — равносторонние,
1) Изучим треугольник ABD.
Т.к. AB=AD (так как являются сторонами ромба), значит, ∆ ABD является равнобедренным треугольником с основанием BD.
Углы при основании равнобедренного треугольника:

Так как каждый угол треугольника ABD равен 60 градусов, значит, ∆ ABD является равносторонним треугольником. Значит, BD=AB.

2) Треугольники ABD и BCD одинаковы по трем сторонам (AB=BC=CD=AD (как стороны ромба), BD=AB (из доказанного)).
То есть, ∆ BCD оказывается равносторонним треугольником.
Что и требовалось доказать.
Т.к. сумма углов ромба, которые прилежат к одной стороне, равна 180º, когда острый угол ромба равен 60º, его тупой угол равен 120º. Таким образом:
Когда тупой угол ромба равен 120 градусам, значит диагональ равняется стороне ромба и делит его на 2 равных равносторонних треугольника.
Ромб с прямыми углами называется квадратом.
Ромб. Формулы, признаки и свойства ромба
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 – 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 – 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://www.calc.ru/Geometricheskiye-Figury-Romb-Ugly-Romba-Kak-Nayti-Ugol-Romba.html
http://ru.onlinemschool.com/math/formula/rhombus/
[/spoiler]
Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формулы косинуса углов через диагональ и сторону:
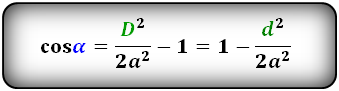
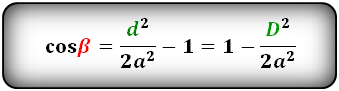
Формулы синуса углов через диагонали :
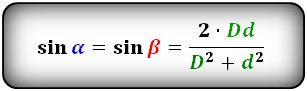
Формулы синуса углов через площадь S и сторону :
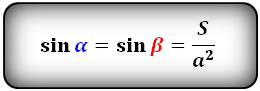
Формулы тангенса половинных углов через диагонали
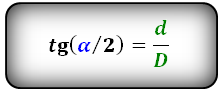
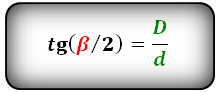
Формулы соотношения острого и тупого углов:

Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
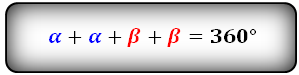
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 25 ноября 2011
-
Обновлено: 13 августа 2021
