В действительности вы задачу озвучили не полностью. Для того чтоб “решить” что то в данной правильной пирамиде надо знать минимум два каких нибудь измерения. Например, что то из основания (сторону, диагональ, пусть половина стороны: MO), поскольку в основании квадрат.
Так же необходимо еще измерение: например высота пирамиды или высота боковой стороны или длина боковой стороны или угол наклона боковой стороны. Поскольку данных нет, не очень понятно, через что выразить ∠DEB (чтоб его найти его надо через некие данные выразить).
Давайте проведем общие исследования. В любом случае надо прийти к ∆DEB
1) ∆DEB – равнобедренный. DE = BE (так как это высоты к боковым сторонам в равных равнобедренных треугольниках ∆BNC и ∆DNC
То есть для нахождения угла, надо “решить” ∆DEB. Для этого надо знать его два элемента.
Например знать сторону BE и сторону BD или пол стороны BO
Тогда sin(∠DEB/2) = OB/BE
Или по т. косинусов cos(∠DEB) = (2BE²-DB²)/2BE² = 1-DB²/2BE²
2) OB можно найти например из данных основания. Пусть дано к примеру MO=q (M-середина AB), тогда MO равна половине стороны квадрата. И ∆OMB – прямоугольный равнобедренный
и OB = q√2
3) Аналогично, зная какой нибудь размер NM или высоту NO или боковую сторону NB, можно найти BE.
Например BE•NB/2 = S = AB•MN/2, откуда BE = AB•MN/NB; При этом NB² = MN² + MB²
BE = 2qMN/NB, NB² = MN²+q²/4
Если вдруг дана была высота NO: то MN² = NO²+OM² = NO² + q²; NB² = NO² + OB² = NO² + 2q²
Все что могло быть выразил.
Могли дать углы. Ну тогда через отношения сторон и косинусов или синусов углов тоже можно выразить.
А так для справки: ∠DEB – будет больше 90˚ и меньше 180˚
Например, если боковые стороны равносторонние ∆, то BE = q√3
sin(∠DEB/2) = √2/√3;
∠DEB = 2•arcsin(√2/√3) ≈ 109,47˚
Тема: Найти угол между двумя плоскостями пирамиды (Прочитано 2311 раз)
0 Пользователей и 1 Гость просматривают эту тему.
В основании пирамиды SABCD лежит прямоугольник ABCD, а все ее боковые ребра одинаково наклонены к основанию. AB:AD:SA=1:корень из 3:2. Точка F-середина АВ, точка К середина АД, точка L середина SC. Найдите угол((FKL),(ABC))
« Последнее редактирование: 11 Сентября 2011, 15:34:30 от Asix »
Задачка с подвохом)) Скоро выложу пояснения….
Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
Задачка с небольшим подвохом)) Угол FKL1 прямой. Что легко доказывается из подобия треугольников: FKO и KmL1. Ну, а дальше все значительно упрощается т.к. искомый угол – это угол LKL1. Надеюсь чертеж поможет)
А угол, как это можно наблюдать, равен 45 градусов.
« Последнее редактирование: 11 Сентября 2011, 13:28:04 от Semen_K »
Пожалуйста не пишите голое условие! Сначало мы выслушаем Ваши мысли или хотябы вопросы, но конкретные и лишь потом дадим необходимые советы!
Но можете всего этого и не делать, если Вас не интересует результат
Если не хотите разбираться сами закажите решение на сайте.
спасибо большое, очень помогли
Найти угол между плоскостями пирамиды
Найти угол между плоскостями пирамиды можно преобразованием чертежа при котором обе грани занимают проецирующее
положение. Таким образом, угол между проекциями плоскостей будет равен углу между плоскостями пирамиды.
Замена плоскостей проекций пирамиды
Для получения проецирующего положения плоскостей пирамиды, можно использовать общее ребро. В примере,
первая замена фронтальной плоскость на плоскость параллельную ребру, вторая замена горизонтальной плоскости на
плоскость перпендикулярную ребру пирамиды. Так как на последней плоскости ребро пирамиды занимает проецирующее
положение, то и прилегающие плоскости граней пирамиды также занимают проецирующее положение и их проекции
выражены отрезками прямых, найденный угол между которыми равен углу между плоскостями.
Плоскопараллельное перемещение пирамиды
Первое плоскопараллельное перемещение выполнено в горизонтальной плоскости до положения фронтали линии пересечения
плоскостей пирамиды. Второе перемещение – во фронтальной плоскости до вертикального положения ребра.
Аналогично замене плоскостей, при проецирующем положении ребра, плоскости пирамиды также оказываются в проецирующем
положении, как результат – найденный угол между проекциями плоскостей пирамиды равен углу между плоскостями.
Угол наклона прямых.
Угол между плоскостями призмы.
Угол между плоскостями параллелепипеда.
Найти угол между плоскостями в кубе.
Презентация угла между плоскостями.
Рисунок угла между плоскостями.
Найти угол.
Решение задач по начертательной геометрии.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
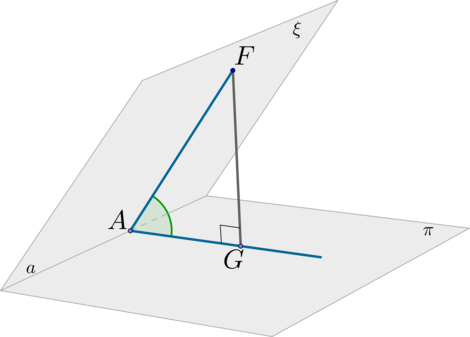
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
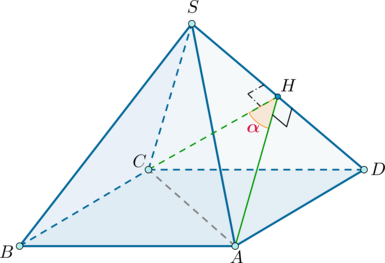
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
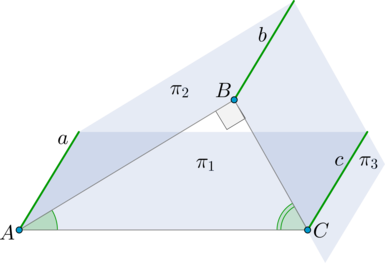
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
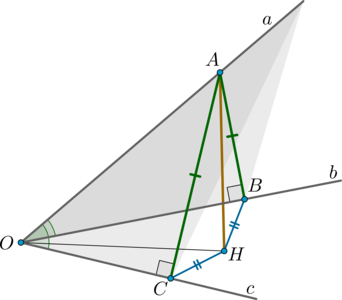
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
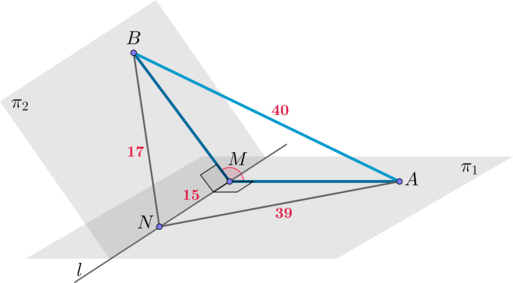
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 – 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 – 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 – 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 – 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
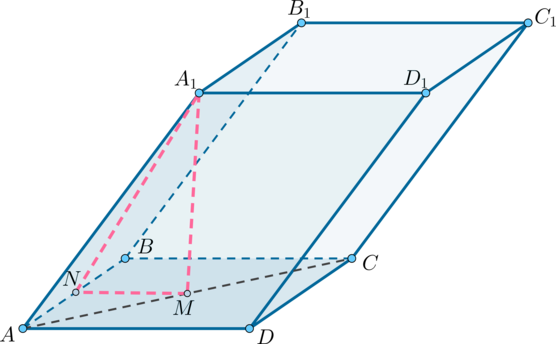
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
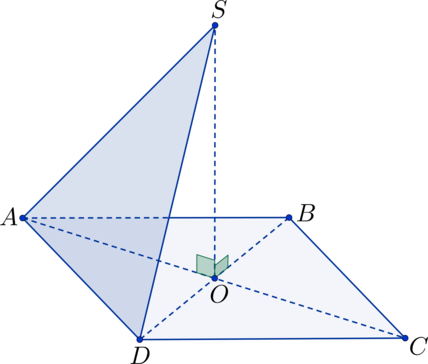
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
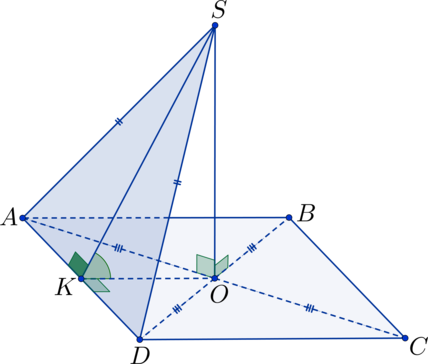
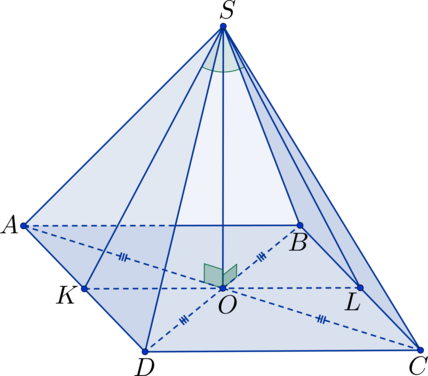
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни
1
МЕТОДЫ НАХОЖДЕНИЯ УГЛОВ МЕЖДУ ПЛОСКОСТЯМ И В. В. Жук, к.ф.-м. н., учитель математики высшей категории, заведующий кафедрой математики РСФМСШИ им. О. Жаутыкова, Алматы Сайт:
2
Основные методы нахождения угла между плоскостями 1.Классический (геометрический) метод 2.Площадь ортогональной проекции 3.Угол между нормалями 4.Угол между плоскостью и нормалью к другой плоскости 5.Векторный метод 6.Теорема о трех синусах 7.Теорема косинусов для двугранного угла 8.Свойства трехгранных углов 9.Метод прямоугольного тетраэдра 1 10.Метод прямоугольного тетраэдра 2 (А. Фельдман) 11. Координатный метод
3
Задача 1. В основании треугольной пирамиды SABC лежит правильный треугольник АВС со стороной 1. Ребро SA пирамиды перпендикулярно плоскости основания, а его длина равна. Плоскость α параллельна прямым SB и АС, а плоскость β параллельна прямым SC и АВ. Найти угол между этими плоскостями.
4
5
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого много- угольника, умноженной на косинус угла между плоскостями много- угольника и его проекции.
6
Задача 1. В основании треугольной пирамиды SABC лежит правильный треугольник АВС со стороной 1. Ребро SA пирамиды перпендикулярно плоскости основания, а его длина равна. Плоскость α параллельна прямым SB и АС, а плоскость β параллельна прямым SC и АВ. Найти угол между этими плоскостями.
7
8
Точка Е – внутри двугранного у α гла величиной α. EF и EG – перпендикуляры на грани угла. Найдите угол FEG равен π – α. Угол между плоскостями равен углу между нормалями к этим плоскостям.
9
Угол между плоскостями равен прямому углу минус угол между одной из этих плоскостей и нормалью к другой плоскости.
10
Задача 2. На ребре СD куба ABCDABCD отметили точку М – середину этого ребра Найти угол между плоскостями (ACD) и (DCM).
11
Задача 1. В основании треугольной пирамиды SABC лежит правильный треугольник АВС со стороной 1. Ребро SA пирамиды перпендикулярно плоскости основания, а его длина равна. Плоскость α параллельна прямым SB и АС, а плоскость β параллельна прямым SC и АВ. Найти угол между этими плоскостями.
12
13
Теорема. В одной из граней двугранного угла, равного γ, проведена прямая, не параллельная его ребру и составляющая с ребром угол, равный α. Если β – угол между данной прямой и плоскостью грани двугранного угла её не содержащей, то. Теорема. В одной из граней двугранного угла, равного γ, проведена прямая, не параллельная его ребру и составляющая с ребром угол, равный α. Если β – угол между данной прямой и плоскостью грани двугранного угла её не содержащей, то.
14
Задача 3. Стороны прямоугольника равны 1 и 2. Меньшая сторона прямоугольника лежит в плоскости π, а диагональ прямоугольника образует с ней угол, равный β. Найти угол между плоскостью π и плоскостью прямоугольника.
15
РЕШИТЕ ЗАДАЧУ 1 С ПОМОЩЬЮ ТЕОРЕМЫ О ТРЕХ СИНУСАХ
16
РЕШИТЕ ЗАДАЧУ 2 С ПОМОЩЬЮ ТЕОРЕМЫ О КОСИНУСОВ ДЛЯ ДВУГРАННОГО УГЛА
17
18
РАССМАТРИВАЛСЯ В ПРЕДЫДУЩЕЙ ЛЕКЦИИ РАССМАТРИВАЛСЯ В ПРЕДЫДУЩЕЙ ЛЕКЦИИ
19
А. Фельдман, Метод прямоугольного Тетраэдра // Математика. 1 сентября, 7, 2012, с
20
РЕШИТЕ ЗАДАЧУ 2 С ПОМОЩЬЮ КООРДИНАТНОГО МЕТОДА Пусть плоскости заданы своими уравнениями: тогда. Пусть плоскости заданы своими уравнениями: тогда.