Как найти угол между двумя сторонами параллелограмма

У параллелограмма 4 угла, это частный случай четырехугольника, у которого противоположные стороны
попарно параллельны. Из этого свойства вытекает равенство противоположных сторон, равенство
противоположных углов и равенство суммы смежных углов двум прямым. Свойства параллелограмма широко
используются в быту и технике.

Острый угол параллелограмма через боковую сторону и высоту

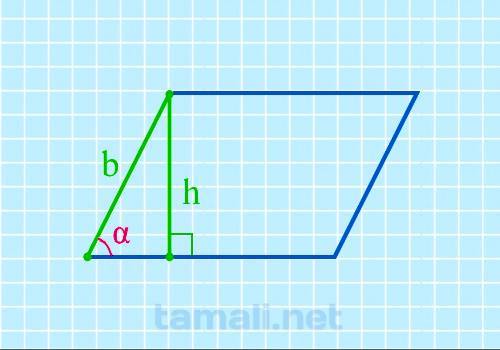
Если известна боковая сторона и высота, то можно найти острый угол параллелограмма по формуле:

sin α = h / b

где α – острый угол, h – высота, b – боковая сторона.

Пример. Пусть h = 4 см, b = 8 см. sin α = h / b = 8 / 4 = 2. α = 90°.

Острый угол параллелограмма через площадь и две стороны

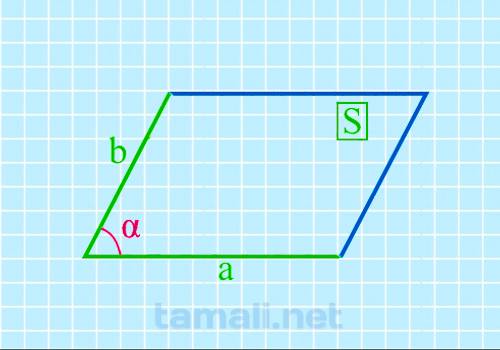
Если известна площадь и две стороны, то можно найти острый угол параллелограмма по формуле:

sin α= S / ab

где α – острый угол, S — площадь параллелограмма, a и b – его стороны.

Пример.  Пусть S=50 м², a=10 м, b=5 м. sin α= S / ab = 50 / (10 * 5) = 1. α = 90°.
Угол прямой, смежные стороны не равны, имеем дело с прямоугольником.

Острый угол параллелограмма через высоту, сторону и периметр

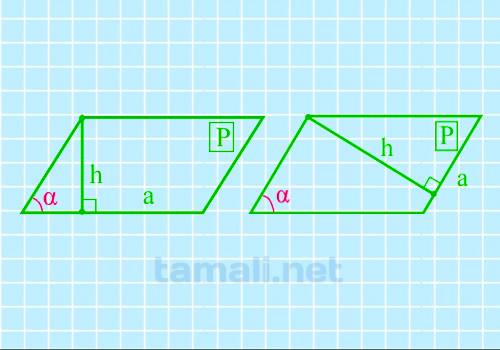
Если известна высота, сторона и периметр, то можно найти острый угол параллелограмма по формуле:

sin α = (2h + a) / P

где α – острый угол, h — высота, a — сторона, P — периметр.

Высота опускается на известную и подставляемую в формулу сторону a. Параллелограмм с заданным
периметром приходится строить, если, например, периметр определен длиной веревки, которую требуется
растянуть на местности в форме параллелограмма.

Пример. Пусть h=10 м, a=15 м, P=70 м. sin α=(2h + a) / P= (2 * 10 + 15) / 70 = 0,5. α = 30°.

Острый угол параллелограмма через две стороны и короткую диагональ

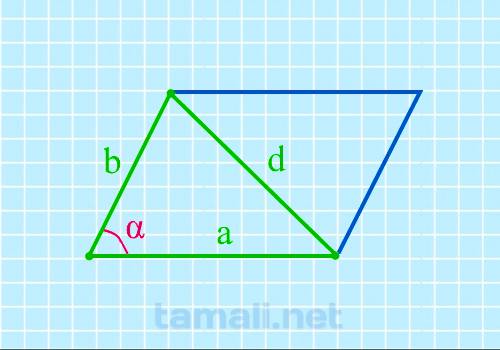
Если известны две стороны и короткая диагональ, то можно найти острый угол параллелограмма по
формуле:

cos α = (a² + b² — d²) / 2ab

где α – острый угол, a и b – стороны параллелограмма, d – его короткая диагональ.

Пример расчета: в данном частном случае 2 прилежащие стороны и короткая диагональ
равны, а именно: a = b = d = 26 мм. cos α=(a² + b² — d²) / 2ab = (26² + 26² — 26²) / (2 * 26 * 26) = 0,5. α=60°.

Из равенства прилежащих сторон следует, что это ромб, а результат расчета показывает, что острый угол
в ромбе равен 60°. Знаете, что это за ромб с подобными размерами? Это нагрудный академический знак
для лиц, окончивших советские высшие учебные заведения, установленный с 1961 года.

Тупой угол параллелограмма через две стороны и длинную диагональ

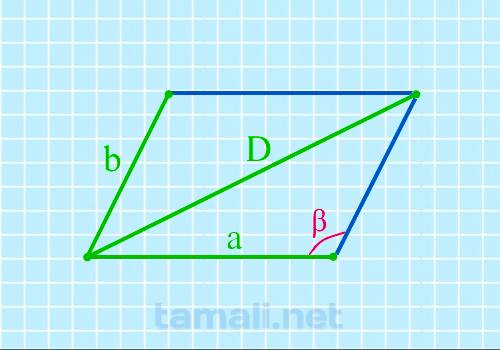
Если известны две стороны и длинная диагональ, то можно найти тупой угол параллелограмма по
формуле:

cos β = (a² + b² — D²) / 2ab

где α – тупой угол, a и b – стороны параллелограмма, D – его длинная диагональ.

Пример расчета: вновь ромб со сторонами a = b = 26 мм и длинной диагональю D=43 мм.
cos β = (a² + b² — D²) / 2ab = (26² + 26² — 43²) / (2 * 26 * 26) = -0,368. α = 112°.
Это опять-таки нагрудный академический знак из предыдущего примера, небольшое отличие полученного
результата от 120° (при остром угле 60° по предыдущему примеру) объясняется округлением исходных
данных до целого числа миллиметров.

Свойства параллелограмма

У любого выпуклого четырехугольника сумма всех внутренних углов равна 360°, исходя из общей формулы
суммы внутренних углов выпуклого многоугольника в градусах s = 180 (n — 2), где n – количество
сторон. Следовательно, если хотя-бы 1 угол параллелограмма равен прямому (90°), остальные 3 угла
также являются прямыми, и параллелограмм вырождается в свой частный вид – прямоугольник.

Если 2 смежные стороны параллелограмма равны, то равны все его 4 стороны, и параллелограмм
вырождается в ромб. И, наконец, если у параллелограмма равны 2 смежные стороны, а угол между ними
прямой, параллелограмм является одновременно и прямоугольником, и ромбом, и вырождается в квадрат.
Зачастую возникает необходимость определения неизвестных характеристик параллелограмма через
известные. Выше ряд примеров подобного рода.

Самый наглядный пример параллелограмма – пантограф электропоезда. При подключении опущенного
пантографа к контактной сети железной дороги изменяется конфигурация пантографа при сохранении длин
сторон, в результате изменяется вертикальная диагональ и происходит касание с подачей электрического
тока.
Форму параллелограмма имеет автомобильный реечный домкрат, велосипедная рама (с
диагональю для увеличения жесткости). Ведь параллелограмм — фигура нежесткая, в отличие от
треугольника. Из нежесткости параллелограмма следует, что знания одних длин сторон недостаточно для
вычисления площади фигуры. Так, пантограф электропоезда можно «сложить» до нулевой площади.
Стеклоочиститель лобового стекла автобуса также представляет собой параллелограмм, и именно
нежесткость фигуры позволяет стеклоочистителю «ометать» при движении стекло.

Здравствуйте, дорогие читатели. В этом выпуске разберемся, что нужно знать из 7 класса для легкого вычисления углов в параллелограмме и трапеции.

Как вы знаете, параллелограмм, прямоугольник, ромб и квадрат – это все параллелограммы. Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны.

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Значит для вычисления углов в параллелограмме и трапеции нам нужно вспомнить теоремы об углах, образованных при пересечении двух параллельных прямых секущей.

1) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 градусам.

Теперь применим это знание для решения задач из ОГЭ.

Задача №1

Для решения, воспользуемся свойством односторонних углов.

Для задания такого типа, можно мысленно продолжить стороны, у вас получится пересечение двух параллельных прямых секущей. Поэтому в данном случае воспользуемся тем, что сумма односторонних углов равна 180 градусов. Больший угол параллелограмма равен 180-61=119

Внимание!!! Будьте внимательны, в задании такого типа может быть написано, что нужно найти меньший угол. Меньший угол – это острый, больший угол – это тупой.

Точно также решается задача №2 с трапецией.

Меньший угол – это острый угол. Значит 180-131=49

Задача №3

Для решения такого типа задачи, нужно найти целый больший угол параллелограмма, он равен 70+35=105.

Найдем меньший угол параллелограмма – он острый, равен 180-105=75

2) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Для этой теоремы подходят следующие задачи:

Задача №4

Решение:

Угол 1 и угол 2 накрест лежащие, значит они раны. Так как АЕ биссектриса, то угол 2 равен углу 3. Значит угол А равен 33+33=66

Задача №5

Решение:

Так как трапеция равнобедренная, то углы при основаниях равны. Значит нам достаточно найти чему равен угол А, тогда мы найдем угол ADC.

Так как накрест лежащие углы при пересечении двух параллельных прямых секущей, равны, то угол А равен 50+30=80, значит угол ADC равен 80

В следующем выпуске, поговорим о том, как найти углы в параллелограмме, где используются другие свойства и теоремы, такие как свойство равнобедренного треугольника, сумма углов треугольника, свойство диагоналей ромба.

Спасибо что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.

Как вычислить угол параллелограмма

У параллелограмма имеется четыре угла. У прямоугольника и квадрата все они равны 90 градусам, у остальных же параллелограммов их значение может быть произвольным. Зная другие параметры фигуры, эти углы можно вычислить.

Инструкция

Параллелограмм -это фигура, у которой противоположные стороны, а также углы равны и параллельны. Существует четыре вида параллелограмма, причем три из них являются частным случаем этой фигуры. У классического параллелограмма два острых и два тупых угла. У квадрата и прямоугольника все углы прямые. Ромб аналогичен классическому параллелограмму и отличается от него лишь тем, что является равносторонним. Все параллелограммы, независимо от вида, имеют ряд общих свойств. Во-первых, диагонали этой фигуры всегда пересекаются в точке, совпадающей с их серединами. Во-вторых, в любом параллелограмме противоположные углы равны.

В ряде задач дан классический параллелограмм с двумя перекрещивающимися между собой диагоналями. Из условия известны две его стороны и площадь. Этого достаточно, чтобы найти один из углов фигуры. Формула связи между площадью, сторонами и углом выглядит так:S=a*b*sin α, где a – длина параллелограмма, b – ширина, α – острый угол, S – площадь.Преобразуйте эту формулу следующим образом:α=arcsin(S/ab).Значение тупого угла β найдите, вычтя значение острого из 180 градусов:β=180-α.

Углы прямоугольника и квадрата находить не требуется – они всегда равны 90°. У ромба же углы могут быть различными, но в связи с одинаковыми длинами всех четырех сторон формула может быть упрощена:S=a^2*sin α, где a – сторона ромба, α – острый угол, S – площадь.Соответственно, угол α равен значению:α=arcsin(S/a^2).Значение тупого угла найдите способом, указанным выше.

Если в параллелограмме или ромбе провести высоту, образуется прямоугольный треугольник. Сторона параллелограмма будет гипотенузой, а высота – катетом этого треугольника. Отношение этого катета к гипотенузе равно синусу угла параллелограмма:sinα=h/c.Отсюда угол α равен:α=arcsin(h/c).

Источники:

• Методика изучения темы “Прямоугольник

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Parallelogram is derived from the Greek word “parallelogrammon” meaning “limited by parallel lines”. So, a parallelogram is a quadrilateral surrounded by parallel lines. Parallelogram is a basic figure in geometry and is a quadrilateral. It is a quadrilateral in which opposite sides are parallel and equal. Parallelogram also has opposite pairs of angles as equal. 

In this article, we will learn more about the properties of a parallelogram, the area, and perimeter of parallelograms, and their examples, in detail.

What is a Parallelogram?

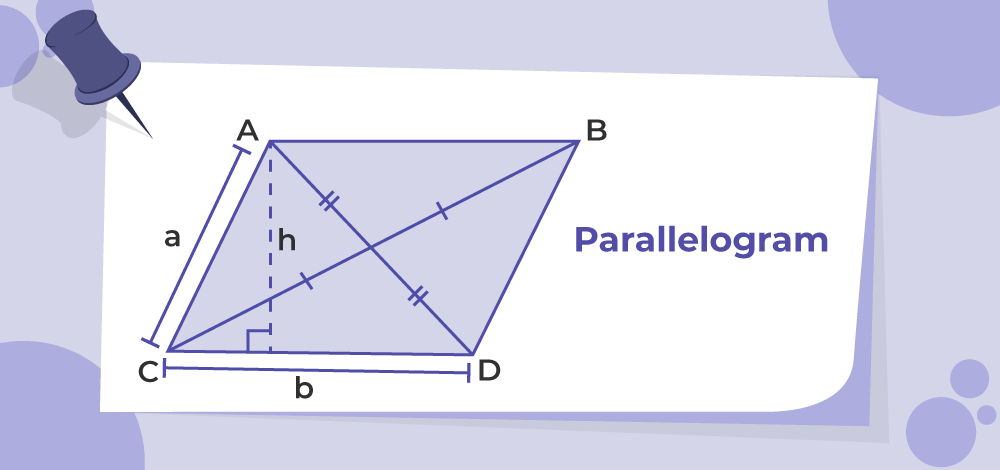
A parallelogram is one of the special types of quadrilateral. The angles between adjacent sides of a parallelogram can vary, but to be a parallelogram, the opposite sides must be parallel. A quadrilateral is a parallelogram if the opposite sides are parallel and equal. Therefore, a parallelogram is defined as a quadrilateral in which two pairs of opposite sides are parallel and equal. Below is the diagram of a parallelogram ABCD having adjacent sides ‘a’ and ‘b’ and height ‘h’.

Real-Life Examples of a Parallelogram

We came across various things in our daily life which resembles a parallelogram. Such as the computer screen, books, buildings, and tiles all are considered to be in a parallelogram shape.

The parallelogram is the most common shape which we encounter daily. Rectangle and square both can be considered a parallelogram and are easily seen in our daily life.

Shape of Parellelogram

A parallelogram is a two-dimensional closed shape with four sides, i.e. it is a quadrilateral. In parallelogram opposite sides are always parallel and equal. Opposite pairs of angles are also equal in parallelograms. In a parallelogram, the interior angle can and can not be a right angle. 

Thus, all rectangles and squares can be considered parallelograms but the opposite is not true, i.e. all parallelograms are not considered to be squares or rectangles.

Special Parallelograms

Some of the special parallelograms which are widely used in geometry are,

Rectangle: It is a special case of the parallelogram in which all the interior angles are equal and their value is equal to 90°.

Square: It is a parallelogram in which all the sides and all the angles are equal and the measure of each interior angle is 90°.

Rhombus: Rhombus is also a parallelogram in which all the sides are equal but all the angles are not equal even though opposite pairs of angles are equal.

Angles of Parallelogram

Parallelogram is a quadrilateral i.e. a polygon with four sides and four angles and the opposite pair of angles are equal in the parallelogram. i.e. in a parallelogram ABCD ∠A is equal to ∠C and ∠B is equal to ∠D.

The sum of all the angles in the quadrilateral is 360°. As a parallelogram is a quadrilateral so sum of all the angles of the parallelogram ABCD equals 360°. Now,

∠A + ∠B + ∠C + ∠D = 360° 

in parallelogram ∠A = ∠C and ∠B = ∠D

Thus,

∠A + ∠B + ∠A + ∠B = 360° 

2(∠A + ∠B) = 360° 

∠A + ∠B = 180°

Similarly, ∠C + ∠D = 180°

Thus, Adjacent angles are supplementry in a parallelogram.

Properties of Parallelogram

There are some special properties of quadrilateral, if applied, make it a parallelogram. Let’s take a look at the properties of parallelograms,

1. The opposite sides of a parallelogram are parallel and equal.
2. The opposite angles of a parallelogram are congruent.
3. If said, one of the angles of a parallelogram is 90°. Then all the angles are 90°, and it becomes a rectangle.
4. The diagonals of the parallelogram bisect each other.
5. The consecutive angles of a parallelogram are supplementary.

Types of Parallelogram

Parallelograms can be classified into several types based on their properties. Based on the properties of a parallelogram and on the sides and angles, the parallelogram is classified into three types,

Rectangle

A rectangle is a parallelogram with two pairs of equal, parallel opposite sides and four right angles. Observe the rectangle ABCD and associate it with the following properties,

1. Two pairs of parallel sides. Here AB || DC and AD || BC
2. Four right angles ∠A = ∠B = ∠C = ∠D = 90°.
3. The opposite sides are the same length, where AB = DC and AD = BC.
4. Two equal diagonals where AC = BD.
5. Diagonals that bisect each other.

Square

A parallelogram with four equal sides and four equal angles is called a square. Observe the square ACDB and associate it with the following properties,

1. Four equal sides are AB = BC = CD = DA.
2. Right angles are ∠A = ∠B = ∠C = ∠D = 90°.
3. There are two pairs of parallel sides. Here AB || DC and AD || BC.
4. Two identical diagonals where AD = BC.
5. Diagonals are perpendicular and bisect each other; AD is perpendicular to BC.

Rhombus

A parallelogram with four equal sides and equal opposite angles is called a rhombus. Consider the diamond ABCD and assign it the following attributes, 

1. In the given figure, the four equal sides are AB = CD = BC = AD. 
2. The two pairs of parallel sides are AB || CD and BC || AD. 
3. The equal opposite angles are ∠A = ∠B and ∠C = ∠D. 
4. Here, the diagonals (AC and BD) are perpendicular to each other and bisect at right angles.

All 2D shapes have two basic formulas for area and perimeter. Let’s discuss these two parallelogram formulas in this section.

Parallelogram Formulas

Parallelogram is a basic 2-dimensional figure which is widely used in mathematics it has various formulas some of them are of Areas and Perimeter

• Area of Parallelogram
• Perimeter of Parallelogram

Let us discuss these two formulas in detail

Area of Parallelogram

The area of ​​a parallelogram is the space between the four sides of the parallelogram. It can be calculated by knowing the length of the base and the height of the parallelogram and measuring it in square units such as cm², m², or inch². Note the following parallelogram representing the base and height.

Consider a parallelogram ABCD with a base (b) and a height (h). The area of ​​a parallelogram is calculated by the formula:

Parallelogram area = base (b) × height (h)

Area of Parallelogram without Height

When the height of the parallelogram is not known, the area of the parallelogram can still be found, provided the angle is known to us. The formula for the area of a parallelogram without height is given as:

Parallelogram area = ab Sinθ

Where a and b are the sides of the parallelogram and θ is the angle between them.

Perimeter of Parallelogram

The perimeter of a parallelogram is the length of its contour, so it is equal to the sum of all sides. In a parallelogram, the opposite sides are equal. Let’s say the sides are a and b. Therefore, the perimeter (P) of a parallelogram with edges is in units of P = 2 (a + b).

Perimeter of Parallelogram = 2 (a + b)

Parallelogram Theorem

Theorem: Parallelograms on the same base and between the same parallels have equal area.

Proof: Let’s assume two parallelograms ABCD and ABEF with the same base DC and between the same parallel lines AB and FC

To Prove: Area of parallelogram ABCD = Area of parallelogram ABEF

In the figure given below, the two parallelograms, ABCD and ABEF, lie between the same parallel lines and have the same base. Area ABDE is common between both parallelograms. Taking a closer look at the two triangles, △BCD and △AEF might be congruent. 

BC = AE (Opposite sides of a parallelogram), 

∠BCD = ∠AEF (These are corresponding angles because BC || AE and CE are the transversal).

∠BDC = ∠AFE (These are corresponding angles because BD || AF and FD are the transversals).

Thus, by the ASA criterion of congruent triangles. These two triangles are congruent, and they must have equal areas. 

area(BCD) = area(AEF)

area(BCD) + area(ABDE) = area(AEF) + area(ABDE) 

area(ABCD) = area(ABEF) 

Hence, parallelograms lying between the same parallel lines and having a common base have equal areas. 

Difference Between Rectangle and Parallelogram

Rectangle and parallelogram are both quadrilaterals, and the rectangle is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a rectangle. Below are the differences in the properties of a rectangle and a parallelogram.

Properties	Parallelogram	Rectangle
Sides	The opposite sides of a parallelogram are equal.	The opposite sides of a rectangle are equal.
Diagonals	The diagonals of a parallelogram bisect each other, but the diagonals are not equal.	The diagonals of a rectangle bisect each other, and the diagonals are equal to each other as well.
Angles	The opposite angles of a parallelogram are equal, and the adjacent angles are supplementary.	All the angles of a rectangle are equal to each other and equal to 90°.

Do Check,

• Area of a Triangle
• Area of a Square
• Area of Rectangle

Solved Examples on Parallelogram

Example 1: Find the length of the other side of a parallelogram with a base of 12 cm and a perimeter of 60 cm.

Solution:

Given perimeter of a parallelogram = 60cm.

Base length of given parallelogram = 12 cm. 

P = 2 (a + b) units 

Where b = 12cm and P = 40cm.

60 = 2 (a + 12)

60 = 2a + 24

2a = 60-24

2a = 36

a = 18cm

Therefore, the length of the other side of the parallelogram is 18 cm. 

Example 2: Find the perimeter of a parallelogram with the base and side lengths of 15cm and 5cm, respectively.

Solution:

Base length of given parallelogram = 15 cm

Side length of given parallelogram = 5 cm

Perimeter of a parallelogram is given by,

P = 2(a + b) units.

Putting the values, we get

P = 2(15 + 5)

P = 2(20)

P = 40 cm

Therefore, the perimeter of a parallelogram will be 40 cm.

Example 3: The angle between two sides of a parallelogram is 90°. If the lengths of two parallel sides are 5 cm and 4 cm, respectively, find the area.

Solution:

If one angle of the parallelogram is 90°. Then, the rest of the angles are also 90°. Therefore, the parallelogram becomes a rectangle. The area of the rectangle is length times breadth.

Area of parallelogram = 5 × 4

Area of parallelogram = 20cm²

Example 4: Find the area of a parallelogram when the diagonals are given as 8 cm, and 10 cm, the angle between the diagonals is 60°.

Solution:

In order to find the area of the parallelogram, the base and height should be known, lets’s first find the base of the parallelogram, applying the law of cosines,

b² = 4² + 5² – 2(5)(4)cos(120°)

b² = 16 + 25 – 40(0.8)

b² = 9

b = 3cm 

Finding the height of the parallelogram,

4/sinθ = b/sin120

4/sinθ = 3/-0.58

sinθ = -0.773

θ = 50°

Now, to find the height,

Sinθ = h/10

0.76 = h/10

h = 7.6cm

Area of the parallelogram = 1/2 × 3 × 7.6
                                         = 11.4 cm²

Example 5: Prove that a parallelogram circumscribing a circle is a rhombus.

Solution:

Given: 

• Parallelogram ABCD
• Circle PQRS

To prove: ABCD is a rhombus.

Proof:

We know that the tangents drawn from an exterior point to a circle are equal to each other. Therefore:

AP = AS ⇢ (1)

BP = BQ ⇢ (2)

DS = DR ⇢ (3)

CR = CQ ⇢ (4)

Adding the LHS and RHS of equations 1, 2, 3, and 4:

AP + BP + DS + CR = AS + BQ + DR + CQ

AB + DR + CR = AS + DS + BC

AB + CD = AD + BC

Since the opposite angles of a parallelogram are equal:

2AB = 2BC

AB = BC, and similarly, CD = AD.

Therefore: AB = CD = BC = AD.

Since all the sides are equal, ABCD is a rhombus.

FAQs on Parallelogram

Q1: What is a parallelogram?

Answer:

A parallelogram is a quadrilateral with opposite pair of lines as parallel and equal. 

Q2: What is the Area of a Parallelogram?

Answer:

The space occupied inside the boundary of the triangle is termed the area of the parallelogram. It can be calculated using the formula,

Area of Parallelogram = Base (b) × Height (h)

Q3: What is the Perimeter of a Parallelogram?

Answer:

The length of all the boundaries of the triangle is termed the perimeter of the parallelogram. It can be calculated using the formula,

Perimeter of Parallelogram = 2(l + b)

where,
l is the length of parallelogram
b is the base of parallelogram

Q4: Does a parallelogram have equal diagonals.

Answer:

No, the diagonals of a parallelogram are not equal. However, the diagonals of a parallelogram bisect each other.

Q5: How many lines of symmetry parallelogram have?

Answer:

In general, a parallelogram has none or 0 lines of symmetry. But in special cases of parallelogram line of symmetry is present. Lines of symmetry of special parallelograms are,

Square	4
Rhombus	2
Rectangle	2

Q6: Does a parallelogram have equal sides?

Answer:

Yes, all parallelograms have equal pairs of opposite sides but not all sides are equal in a parallelogram.

Q7: Is a rhombus a parallelogram?

Answer:

Yes, a rhombus is a parallelogram. A rhombus has all the properties of the parallelogram and more. 

Q8: How is a parallelogram different from a quadrilateral?

Answer:

All parallelograms are quadrilaterals, but not all quadrilaterals are necessarily parallelograms. For example, a trapezoid is a quadrilateral, not a parallelogram. For a quadrilateral to be a parallelogram, all opposite sides must be parallel and equal.

Q9: Is a square a parallelogram?

Answer:

Yes, a square is a parallelogram as it has all the properties of a parallelogram and more since a square has some extra properties (For example, all angles are right angles, etc.), all parallelograms are not squares.

Q10: Is a rectangle a parallelogram?

Answer:

Yes, a rectangle is a parallelogram. Rectangle is a parallelogram as it has all the properties of a parallelogram and more. However, a parallelogram is not always a rectangle.