Как найти угол между гранями пирамиды решение

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)

Краткая теория

---

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды 
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

 найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

Угол между ребрами

 и

 найдем как угол
между направляющими векторами

  и

:

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

 и гранью

.

Для этого вычислим
координаты нормального вектора плоскости

 –им будет
векторное произведение векторов 

 и

.

 

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

  

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

    и 

:

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

  и

:

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

.  Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

 

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

 -уравнение
грани

 

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

 из вершины

:

Нормальный вектор

 является
направляющим вектором высоты, кроме того, высота проходит через точку

 

Искомое уравнение
высоты:

Сделаем схематический чертеж:

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, – это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово “пирамида”. Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

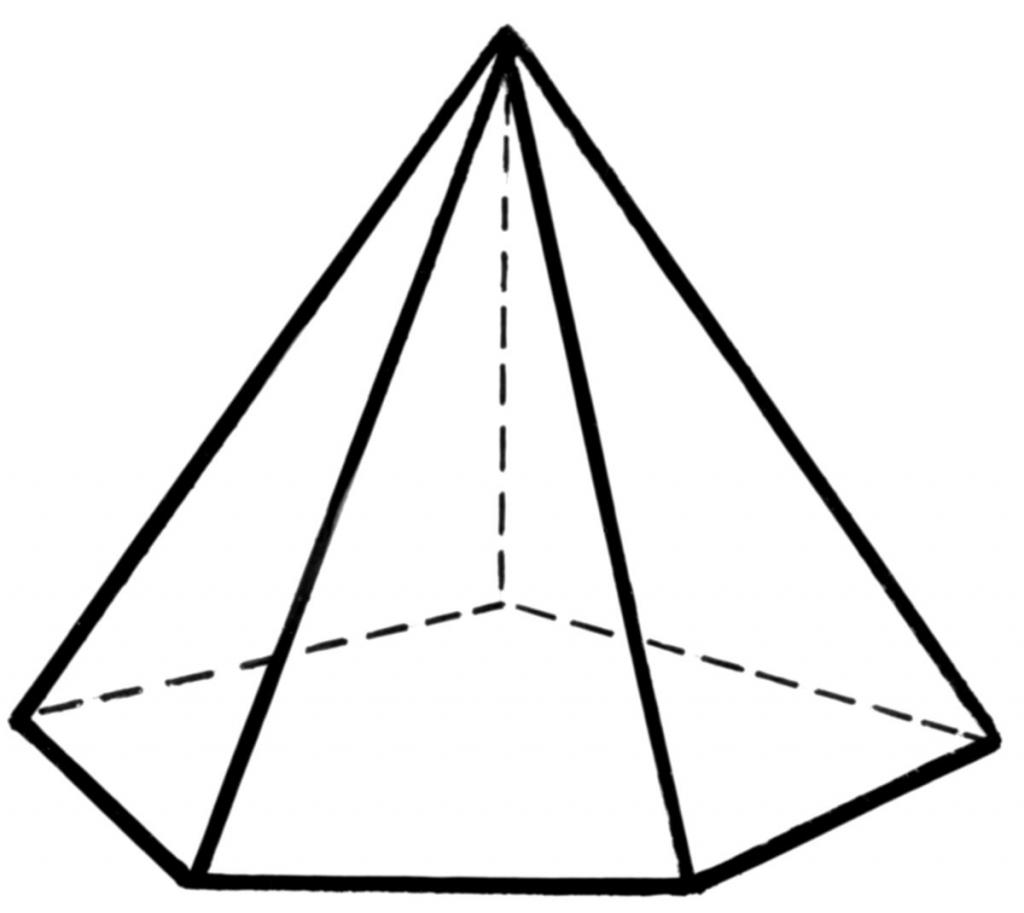
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

Двугранные углы фигуры

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n – число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип – на боковых ребрах.

Как рассчитать углы пирамиды?

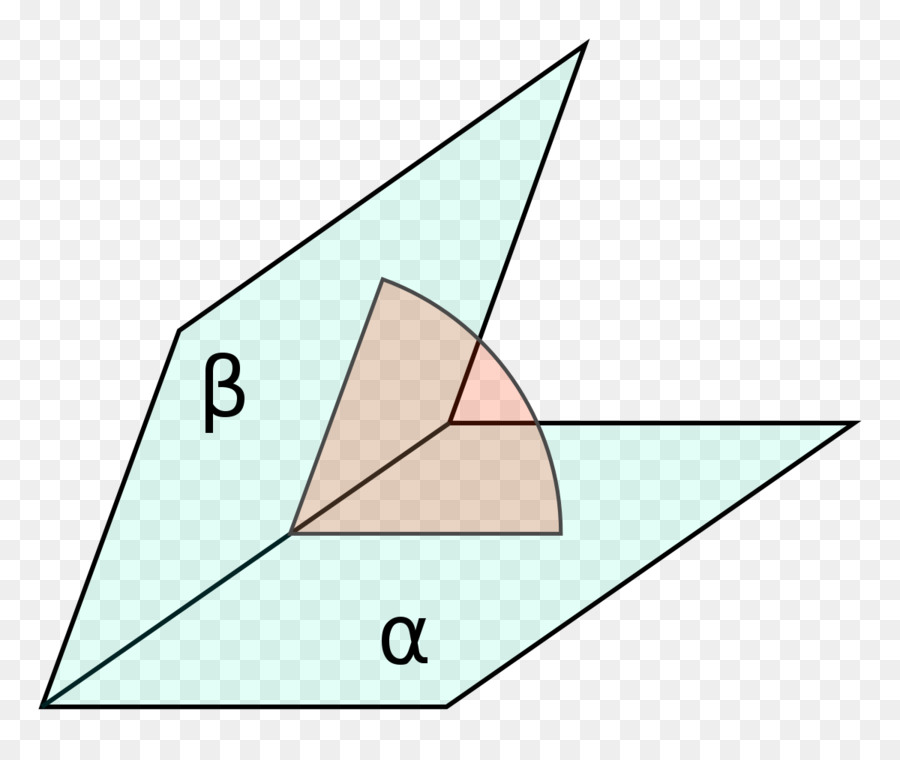
Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D – это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

n¯ = [A; B; C]

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

n₁¯ = [A₁; B₁; C₁];

n₂¯ = [A₂; B₂; C₂]

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

φ = arccos(|(n₁¯*n₂¯)|/(|n₁¯|*|n₂¯|))

Или в координатной форме:

φ = arccos(|A₁*A₂ + B₁*B₂ + C₁*C₂|/(√(A₁² + B₁²+C₁²)*√(A₂² + B₂² + C₂²)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

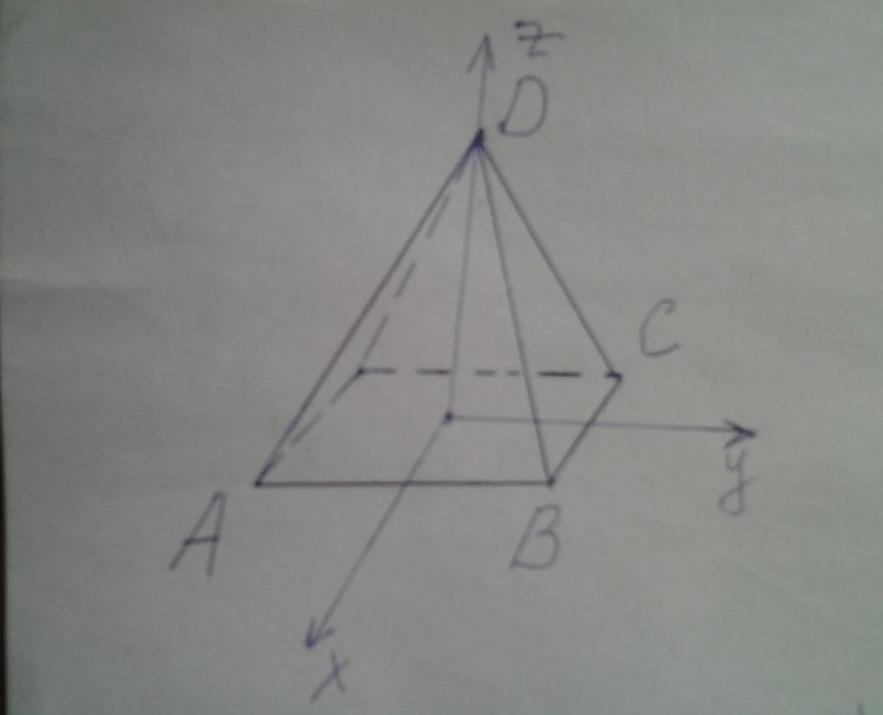
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

A(a/2; -a/2; 0);

B(a/2; a/2; 0);

C(-a/2; a/2; 0);

D(0; 0; h)

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Для ABC:

AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n₁¯ = [AB¯*AC¯] = (0; 0; a²)

Для ABD:

AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n₂¯ = [AB¯*AD¯] = (a*h; 0; a²/2)

Для BCD:

BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n₃¯ = [BC¯*BD¯] = (0; a*h; a²/2)

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

(n₁¯*n₂¯) = a⁴/2; |n₁¯| = a²; |n₂¯| = a*√(h² + a²/4);

φ = arccos(a⁴/2/(a²*a*√(h² + a²/4))) = arccos(a/(2*√(h² + a²/4))) = 67,38^o

Угол между ABD и BDC:

(n₂¯*n₃¯) = a⁴/4; |n₂¯| = a*√(h² + a²/4) ; |n₃¯| = a*√(h² + a²/4);

φ = arccos(a⁴/(4*a²*(h²+a²/4)) = arccos(a²/(4*(h²+a²/4))) = 81,49^o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

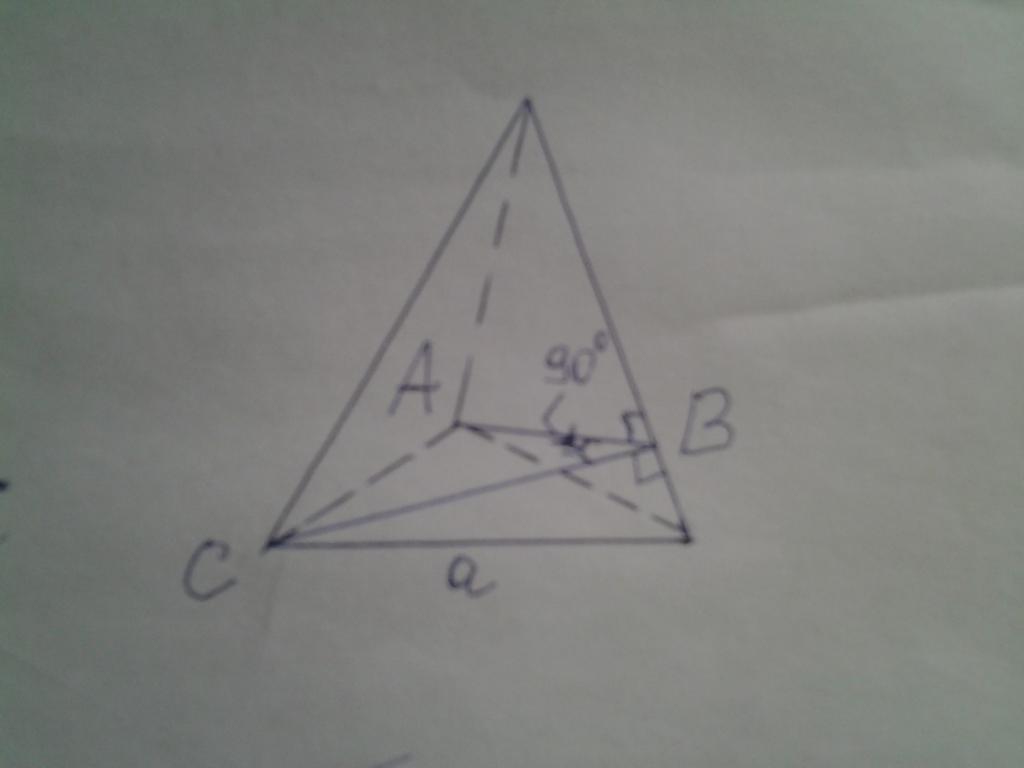
Двугранный угол, равный 90^o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры – h, апофему – h_b и боковое ребро – b. Теперь можно записать следующие формулы:

S = 1/2*a*h_b;

b² = h_b² + a²/4;

b² = h² + a²/3

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

x = a/√2;

S = 1/2*b*a/√2

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

1/2*a*h_b = 1/2*b*a/√2 =>

h_b = b/√2;

b² = b ²/2 + a²/4 =>

b = a/√2;

a²/2 = h² + a²/3 =>

a = h*√6

Площадь равностороннего треугольника рассчитывается так:

S = √3/4*a² = 3*√3/2*h²

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см².

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Двугранные углы пирамиды и методика их расчета

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, – это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово “пирамида”. Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Вам будет интересно: Популяция людей: определение, виды, свойства и примеры

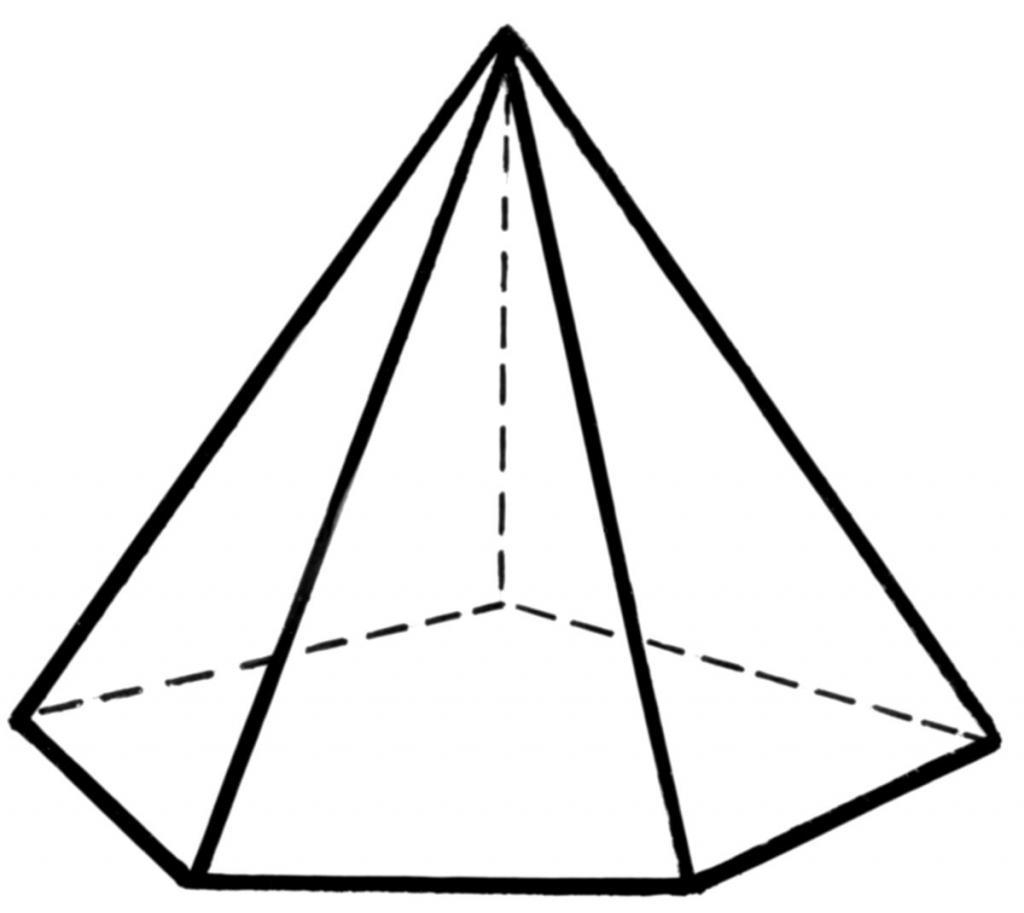
Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

Двугранные углы фигуры

Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n – число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип – на боковых ребрах.

Как рассчитать углы пирамиды?

Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D – это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

Или в координатной форме:

φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

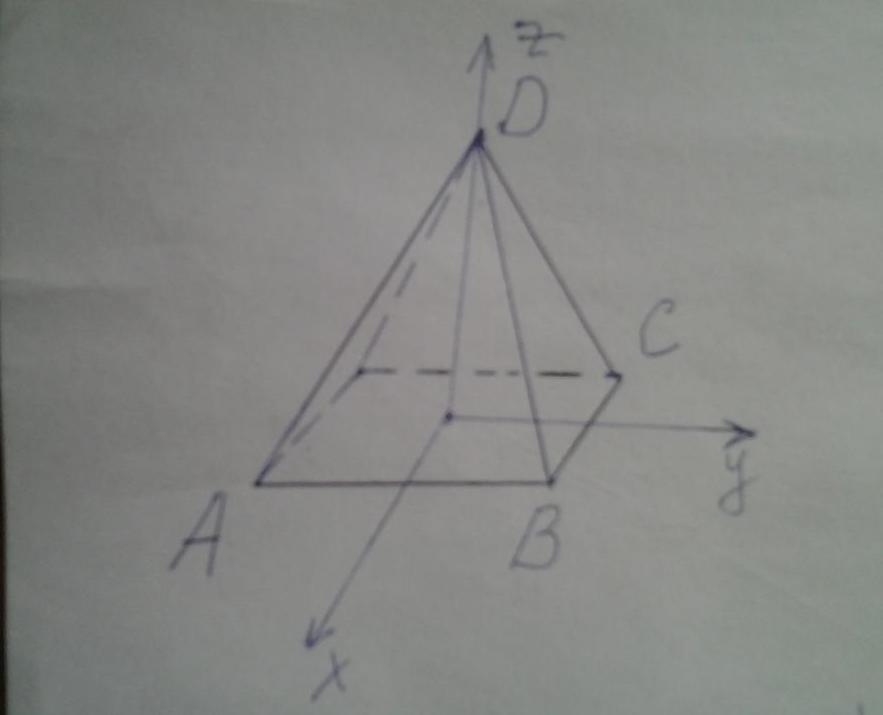
Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

AB¯ = (0; a; 0); AC¯ = (-a; a; 0); n1¯ = [AB¯*AC¯] = (0; 0; a2)

AB¯ = (0; a; 0); AD¯ = (-a/2; a/2; h); n2¯ = [AB¯*AD¯] = (a*h; 0; a2/2)

BC¯ = (-a; 0; 0); BD¯ = (-a/2; -a/2; h); n3¯ = [BC¯*BD¯] = (0; a*h; a2/2)

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

(n1¯*n2¯) = a4/2; |n1¯| = a2; |n2¯| = a*√(h2 + a2/4);

φ = arccos(a4/2/(a2*a*√(h2 + a2/4))) = arccos(a/(2*√(h2 + a2/4))) = 67,38o

Угол между ABD и BDC:

(n2¯*n3¯) = a4/4; |n2¯| = a*√(h2 + a2/4) ; |n3¯| = a*√(h2 + a2/4);

φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

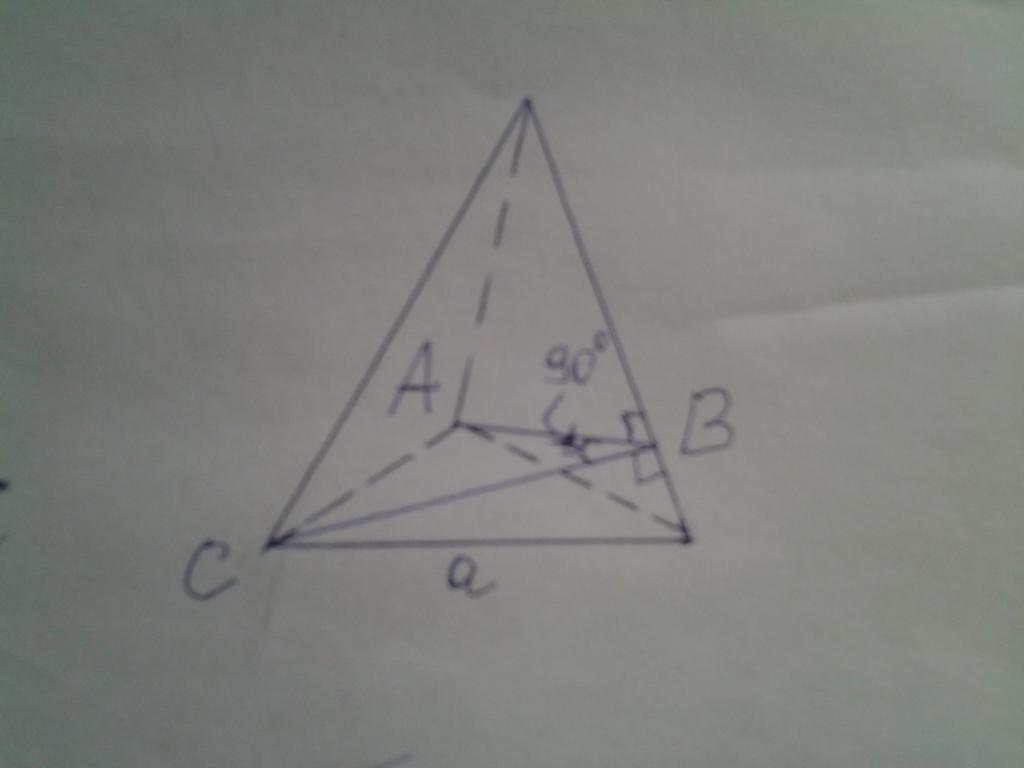
Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры – h, апофему – hb и боковое ребро – b. Теперь можно записать следующие формулы:

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

Площадь равностороннего треугольника рассчитывается так:

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.

Геометрические фигуры. Пирамида. Углы пирамиды.

Углы простейшей пирамиды – тетраэдра, все равняются 60 градусам, как в треугольнике, который лежит в основании, так и в треугольниках образующих граней.

Углы прямоугольной пирамиды, угол в основании, между сторонами квадрата 90°, а в треугольниках образующих граней – 60°. В диагональном сечении, в треугольнике, угол в вершине пирамиды 90°, и 2 угла у основания 45°.

Соседние двугранные углы при основании пирамиды равны.

Если соседние двугранные углы при основании пирамиды равны, значит, вершина пирамиды проецируется на биссектрису угла между соответствующими соседними ребрами основания.

SO – высота пирамиды. Тогда т. O лежит на биссектрисе BM.

Треугольная пирамида, с одной боковой гранью перпендикулярной основанию, а 2 другие наклонены к основанию под одинаковыми углами.

Когда в треугольной пирамиде 1 из боковых граней перпендикулярна основанию, а 2 оставшиеся образуют с основанием одинаковые углы, значит высота пирамиды оказывается высотой боковой грани, а ортогональная проекция вершины пирамиды — основанием биссектрисы треугольника, лежащего в основании пирамиды.

Значит SO — это высота пирамиды и она лежит в боковой грани SAC, а BO — биссектриса треугольника ABC, т.е.:

Пирамиды, в которых все двугранные углы при основании равны.

Когда все двугранные углы при ребрах основания равны, значит:

1) Вершина пирамиды проецируется в центр вписанной в основание окружности;

2) Основание пирамиды – это ортогональная проекция ее боковой поверхности, поэтому площадь основания пирамиды находят по формуле.

где – двугранный угол при основании пирамиды.

Зачастую эту формулу используют для определения площади боковой поверхности пирамиды:

Значит, площадь полной поверхности пирамиды равняется:

3) Площадь боковой поверхности в этом случае тоже находят по формуле:

где p — полупериметр основания, l — высота боковой грани, проведенная из вершины пирамиды.

[spoiler title=”источники:”]

http://1ku.ru/obrazovanie/41949-dvugrannye-ugly-piramidy-i-metodika-ih-rascheta/

http://www.calc.ru/Geometricheskiye-Figury-Piramida-Ugly-Piramidy.html

[/spoiler]

План урока:

Понятие пирамиды

Правильная пирамида

Усеченная пирамида

Типичные задачи на пирамиды

Понятие пирамиды

Построим на некоторой плос-ти α произвольный многоугольник А₁А₂…А_n. Далее отметим в пространстве точку Р, не принадлежащую плос-ти α. Соединив точку Р с вершинами многоуг-ка получим многогранник, который именуется пирамидой (в различной литературе может использоваться сокращение пирам-а).

Та единственная точка Р, не находящаяся в одной плос-ти со всеми остальными вершинами, именуется вершиной пирам-ы. Многоугольник, образованный остальными вершинами – это основание пирамиды.

Основанием пирам-ы может быть многоугольник с любым количеством сторон. Если в основании лежит, например, пятиугольник, то и пирам-у называют пятиугольной. Если же в основании находится десятиугольник, то это будет уже десятиугольная пирам-а. В общем случае пирам-у, у которой в основании располагается n-угольник, именуется n-угольной. Ясно, что треугольная пирам-а и тетраэдр – это по сути одна и та же фигура.

Все грани пирам-ы, за исключением ее основания, именуются боковыми гранями. Понятно, что каждая боковая грань – это треугольник. Ребра пирамиды, выходящие из ее вершины, именуются боковыми ребрами пирамиды.

Посчитаем количество ребер, вершин и граней пирам-ы. Если она n-угольная, то у неё (n + 1) вершин (n точек в основании и ещё одна точка, не лежащая в основании). Также у нее (n + 1) граней, из них одна – это основание, а остальные n – боковые грани пирамиды (по одной на каждую сторону n-угольника). Наконец, у пирам-ы n ребер находятся в плос-ти основания, а ещё n ребер являются боковыми. Итого имеем 2n ребер. Теперь можно убедиться, что теорема Эйлера для пирам-ы выполняется:

Из вершины пирам-ы можно опустить перпендикуляр на плос-ть основания. Он будет именоваться высотой пирамиды.

Как и в случае с призмой, можно подсчитать площадь боковой поверхности призмы, которую обозначают как S_бок. Если же к ней ещё добавить и площадь основания (S_осн), то в сумме получится уже площадь полной поверхности призмы (S_полн). Эту связь между величинами можно представить в виде формулы:

Правильная пирамида

Особый интерес и в геометрии, и в реальной жизни представляют так называемые правильные пирамиды. Их отличают две особенности:

1) в их основании находится правильный многоугольник;

2) высота пирам-ы падает на основание в точке, являющейся центром этого правильного многоуг-ка.

Напомним, что центром правильного многоуг-ка считается центр описанной около него окружности, который одновременно является и центром вписанной окружности.

Действительно, опустим из вершины Р правильной пирам-ы высоту РО. Тогда О будет центром описанной окружности:

Примечание. На рисунках, показывающих объемные фигуры, окружности искажают свою форму и выглядят как эллипсы, то есть овалы.

Построим из О радиусы ОА₁, ОА₂, ОА₃,… Они все будут одинаковы, ведь это радиусы одной и той же окружности. Также заметим, что высота правильной пирамиды РО будет перпендикулярна каждому из этих радиусов, ведь она перпендикулярна и всей плос-ти. Это значит, что ∆РОА₁, ∆РОА₂, ∆РОА₃… – прямоугольные. При этом у них есть общий катет РО, а катеты ОА₁, ОА₂, ОА₃… одинаковы. Значит, эти треугольники равны. Отсюда и вытекает, что их гипотенузы, то есть боковые ребра РА₁, РА₂, РА₃…, также одинаковы, ч. т. д.

Заметим, что можно доказать и почти противоположное утверждение – если у пирам-ы боковые ребра одинаковы, а в основании находится правильный многоуг-к, то она является правильной. Для доказательства предположим, что ребра РА₁, РА₂, РА₂… одинаковы. Опустим из Р высоту, которая упадет в некоторую точку О. Теперь соединим эту точку с вершинами А₁, А₂, А₃… Получатся прямоугольные ∆РОА₁, ∆РОА₂, ∆РОА₃… У них есть общий катет (высота РО) и одинаковые гипотенузы. Значит, эти треугольники равны, и потому одинаковы отрезки ОА₁, ОА₂, ОА₃… Это значит, что точка О равноудалена от вершин многоуг-ка, и если из нее провести окружность радиусом ОА₁, то она также пройдет через остальные вершины многоуг-ка. То есть эта окружность окажется описанной. Это и означает, что точка О – центр многоуг-ка, и тогда вся пирам-а оказывается по определению правильной.

Из равенства боковых ребер напрямую вытекает и тот факт, что все боковые грани правильной пирам-ы – одинаковые равнобедренные треугольники. Высоты, проведенные в этих равнобедренных треугольниках к основанию правильной пирамиды, именуются апофемами.

Ещё раз уточним, что понятие апофемы применимо только к правильной пирам-е. У других пирамид тоже можно на боковых гранях провести высоты к основанию, но они просто не будут называться апофемами пирамиды.

Ясно, что раз в правильной пирам-е все боковые грани – равные друг другу равнобедренные треуг-ки, то и их высоты, то есть апофемы, одинаковы. Также можно утверждать, что каждая апофема делит ребра, на которое она падает, пополам, ведь высоты в равнобедренном треуг-ке – это ещё и медианы.

Апофема используется для вычисления площади боковой поверхности пирам-ы, так как существует такая теорема:

Докажем ее. Пусть у правильной n-угольной пирам-ы в основании находится многоуг-к со стороной а. Тогда его периметр Р вычисляется так:

Каждая боковая грань пирам-ы – это треугольник. Проведем на них апофемы, которые одновременно окажутся и высотами для этих треугольников. Если мы обозначим длину апофемы как d, то площадь каждой грани можно рассчитать по простейшей формуле площади треугольника:

Усечённая пирамида

Возьмем произвольную пирам-у, а далее секущую плоскость, которая будет параллельна основанию, причем она будет пересекать ребра РА₁, РА₂, РА₃… в точках В₁, В₂, В₃… соответственно. В результате, отбросив «верхушку» пирам-ы, мы получим новую фигуру, которая именуется усеченной пирамидой.

У усеченной пирам-ы уже не одна, а две грани считаются основаниями, и они параллельны друг другу. Большее из них именуют нижним основанием, а меньшее – верхним основанием.

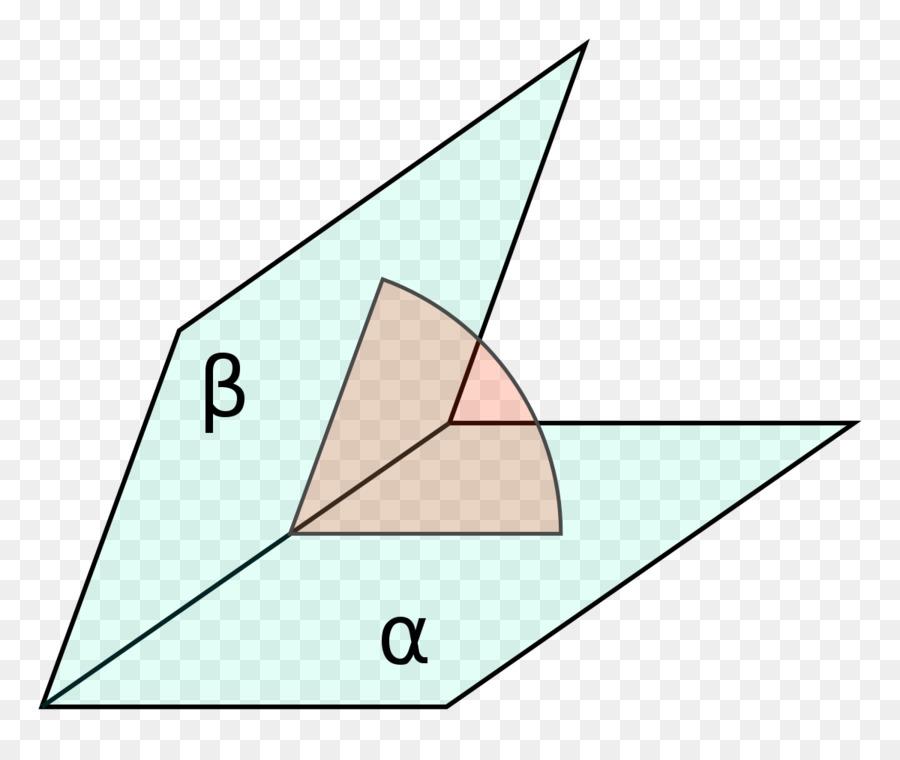
Докажем, что боковые грани любой усеченной пирам-ы – это трапеции. Действительно, обозначим плос-ть верхнего основания как α, нижнее основание как β, а произвольную грань как γ:

Нам надо доказать, что А₁А₂В₂В₁ – это трапеция. Действительно, прямые А₁А₂ и В₁В₂ не могут скрещиваться, ведь они располагаются в единой плос-ти γ. Не могут они и пересекаться, ведь тогда точка их пересечения была бы общей для плос-тей α и β, а эти плос-ти параллельны. Остается один вариант: А₁А₂||В₁B₂. Две другие стороны грани, А₁В₁ и А₂В₂, будут пересекаться в точке Р, вершине исходной пирам-ы. Тогда по определению две четырехугольник А₁А₂В₂В₁ будет трапецией, ведь у него две стороны параллельны, а две другие – нет.

Отдельно отметим, что усеченная пирам-а, полученная из правильной пирам-ы, также называется правильной, а высоты ее боковых граней также именуются апофемами. Докажем одну теорему:

Действительно, пусть из правильной пирам-ы с вершиной в Р получена правильная усеченная пирамида с основаниями А₁А₂А₃…A_n и В₁В₂В₃…B_n:

Так как исходная пирам-а – правильная, то ее грани – равные равнобедренные треугольники, у которых одинаковы углы при основаниях:

Мы уже знаем, что грани А₁А₂В₂В₁ и А₂А₃В₃В₂ – трапеции. Раз у них одинаковы углы при основании, то можно утверждать, что эти трапеции – равнобедренные. Это значит, что любые два боковых ребра, находящиеся на одной грани, одинаковы. Значит, одинаковы вообще все боковые ребра. Получается, что все боковые грани – это равнобедренные трапеции с одинаковыми основаниями, боковыми сторонами и углами при основании. Этого достаточно для того, чтобы считать эти трапеции равными, ч. т. д.

Из этой теоремы вытекает тот факт, что стороны многоуг-ка, образующего верхнее основание, одинаковы. Более того, углы этого многоуг-ка равны таким же углам в нижнем основании. Например, ∠А₁А₂А₃ = ∠В₁В₂В₃. Действительно, мы знаем, что А₁А₂||В₁В₂ и А₂А₃||B₂B₃, и потому стороны углов ∠А₁А₂А₃ = ∠В₁В₂В₃ оказываются сонаправленными лучами.

Так как в нижнем многоуг-ке А₁А₂А₃…A_n все углы одинаковы (ведь он правильный), то и в верхнем многоуг-ке В₁В₂В₃…B_n также будут одинаковы углы. В итоге можно утверждать, что верхнее основание усеченной пирамиды является правильным многоуг-ком, также как и нижнее.

Отметим ещё один факт. При построении секущей плос-ти пирам-а делится на две части. Нижняя из них – это усеченная пирам-а, а верхняя – это обычная пирам-а, меньшая исходной. Докажем, что если исходная пирам-а РА₁А₂А₃…Р_n была правильной, то оставшаяся после отсечения «верхушка» также будет правильной пирам-ой. Мы уже выяснили, что ее основание В₁В₂В₃…В_n– правильный многоуг-к. Отрезки РА₁, РА₂, РА₃… одинаковы как боковые ребра исходной правильной пирам-ы. В свою очередь отрезки А₁В₁, А₂В₂, А₃В₃ одинаковы как боковые ребра правильной усеченной пирам-ы. Но отсюда получается, что одинаковы также и отрезки РВ₁, РВ₂, РВ₃… Значит, в пирам-е РВ₁В₂В₃…В_n в основании лежит правильный многоуг-к, а ее боковые ребра одинаковы. Из этого вытекает, что эта пирам-а – правильная.

Ещё одна теорема позволяет вычислять площадь боковой поверхности правильной усеченной пирам-ы:

Действительно, каждая грань такой пирам-ы – это трапеция. Обозначим длину ее верхнего основания буквой а, а нижнего – буквой b.Тогда, если основания пирам-ы – это многоуг-ки с n сторонами, периметр этих оснований будет вычисляться так:

Теперь проведем на каждой боковой грани апофему, чья длина будет обозначаться как d. Тогда, используя формулы площади трапеции, сможем вычислить площадь грани:

Типичные задачи на пирамиды

Рассмотрим несколько задач, в которых фигурируют пирам-ы. Перед просмотром решения попытайтесь решить их самостоятельно.

Задание. Существует ли пирамида, у которой ровно 999 ребер?

Решение. Если в основании пирам-ы находится n-угольник, то у нее 2n ребер. Так как n– целое число, то 2n будет уже четным числом. То есть количество ребер у любой пирам-ы всегда четно. Поэтому не существует пирам-ы с 999 ребрами, ведь 999 – нечетное число.

Задание. Верно ли, что всякий правильный тетраэдр одновременно является и правильной пирам-ой? И наоборот, является ли каждая правильная треугольная пирам-а правильным тетраэдром?

Решение. Напомним, что правильный тетраэдр – это тетраэдр, у которого все ребра одинаковы. Если одну из вершин тетраэдра принять за вершину пирам-ы, то получится, что в ее основании равносторонний треугольник, который, как мы знаем, является правильным многоуг-ком. Также окажется, что все боковые ребра пирам-ы также одинаковы. Это значит, что она – правильная.

Теперь посмотрим на произвольную правильную треугольную пирам-у. Будет ли она обязательно правильным тетраэдром? Нет, ведь ее боковые ребра могут отличаться по длине от ребер, находящихся в основании. Например, в основании может находиться равносторонний треуг-к со стороной 5 см, а боковое ребро правильной пирамиды может иметь длину 10 см. Таким образом, можно считать правильный тетраэдр лишь частным случаем правильной пирам-ы.

Задание. В основании пирам-ы находится ромб со стороной 5 см.Одна из его диагоналей имеет длину 8 см. Высота пирам-ы имеет длину 7 см и проходит через точку, в которой пересекаются диагонали ромба. Вычислите длину боковых ребер.

Решение.

Обозначим ромб в основании как АВСD, а вершину пирам-ы буквой Р. Пусть диагонали пересекаются в точке О, тогда РО – высота. Также пусть диагональ АС равна 8 см. По свойству ромба О будет серединой диагоналей, поэтому

Отрезок OD будет иметь ту же длину 3 см, ведь О – середина BD.

Так как высота РО перпендикулярна всем прямым в плос-ти основания, то ∆АОР, ∆ВОР, ∆СОР, ∆DOP – прямоугольные, и боковые ребра пирам-ы будут гипотенузами этих треугольников. Вычислим АР по теореме Пифагора:

Задание. В основании пирам-ы лежит квадрат, а одно из ее боковых ребер перпендикулярно основанию. Одна из боковых граней образует с плос-тью основания угол в 45°. Длина длиннейшего ребра пирам-ы составляет 12 см. Определите высоту пирам-ы и площадь ее боковой поверхности.

Решение.

Обозначим квадрат, находящийся в основании, как АВСD, а вершину пирам-ы как Р. Пусть ребро PD перпендикулярно основанию. Тогда PD⊥AD и PD⊥CD. Ясно, что PD как раз и является искомой нами высотой пирам-ы.

Теперь надо понять, какие углы в пирам-е составляют 45° и какое ребро равно 12 см. Грани ADP и СDP проходят через перпендикуляр PDк основанию, а потому они перпендикулярны основанию. Значит, угол в 45° с основанием образует либо грань АВР, либо грань СВР.

Заметим, что АВ⊥AD (это смежные стороны квадрата), а AD – это проекция ребра АР на основание. Тогда по теореме о трех перпендикулярах АВ⊥АР. Аналогично из того факта, что ВС⊥СD, вытекает, что ВС⊥СР. Также заметим, что ∆ADP и ∆СDP прямоугольные, имеют общий катет PD и одинаковые катеты AD и CD (это стороны квадрата). Значит, это равные треугольники, и

∠PAD = ∠PCD

Грань АВР пересекается c основанием по прямой АВ, причем AD⊥АВ и АР⊥АВ. Значит, ∠РАD – это угол между гранью АВР и основанием. Аналогично и ∠РСD является углом между гранью СВР и основанием. Но эти углы одинаковы. Значит, каждый из этих углов будет равен 45°, иначе в пирам-е не останется угла между плос-тями, который мог бы составлять 45°.

Ясно, что ребро АР длиннее ребра РD, ведь в прямоугольном ∆ADP АР – это гипотенуза, а РD катет (гипотенуза всегда длиннее катета). Теперь заметим, что ∆РАВ и ∆РСВ – также прямоугольные, ведь АВ⊥АР и ВС⊥СР. Но в них гипотенузой является уже РВ, то есть РВ длиннее АВ, ВС, АР и РС. Так как отрезки AD и AC равны АВ как стороны квадрата, получаем, что именно ребро РВ – длиннейшее в пирам-е, то есть его длина составляет 12 см.

В прямоугольном ∆ADP∠PAD = 45°. Это значит, что ∆ADP является прямоугольным и равнобедренным, то есть AD = PD. Обозначим искомую нами длину РD как x. Теперь проведем диагональ BD:

Её длину можно вычислить из ∆ADB:

Итак, высоту нашли, теперь нужно рассчитать боковую площадь. Но для этого предварительно найдем АР из ∆АРD:

Такую же длину имеет и РС, ведь ∆АРD и ∆СРD равны.

Мы уже выяснили, что каждая боковая грань – прямоугольный треугольник. Зная длины катетов, легко найдем площадь каждой грани:

Задание. В правильной шестиугольной пирам-е ребро при основании равно 3 см. Высота этой пирам-ы составляет 4 см. Вычислите длину апофемы этой пирам-ы, а также угол, который ее боковые грани образуют с основанием.

Решение.

Основание пирам-ы обозначим как АВСDEF, а вершину как Р. Пусть РО – высота, тогда О – центр описанной окружности. Напомним, что у правильного шестиугольника радиус описанной окружности совпадает с длиной его стороны, то есть

Теперь надо найти угол между гранью АВР и основанием. Они пересекаются по прямой АВ. РН⊥АВ, ведь РН – апофема. ОН – это проекция РН на основание. Так как АВ⊥РН, то по обратной теореме о трех перпендикулярах и ОН⊥АВ. Значит, ∠ОНР и является искомым углом между гранью АВР и основанием. Для его вычисления применим тригонометрию к ∆ОНР:

Задание. В правильной шестиугольной пирам-е все ребра имеют длину, равную единице. Найдите угол между прямыми АР и BD:

Решение. Для нахождения угла между АР и BD, у которых нет общей точки, можно вычислить угол между прямыми, которые будут им параллельны. Легко заметить, что АЕ||BD. Докажем это, рассмотрев основание пирам-ы:

Каждый угол правильного шестиугольника составляет 120°. В частности, это относится к ∠F и ∠С. ∆АFЕ – равнобедренный, ведь его стороны FE и AF одинаковы. Тогда и углы при основании будут одинаковыми. Найдем их:

Аналогично можно определить, что все углы четырехугольника АВDE прямые, то он представляет собой прямоугольник. Его противоположные стороны параллельны, в частности, АЕ||BD. Это означает, что искомый нами угол – это ∠РАЕ:

Для его вычисления необходимо вычислить длины сторон ∆РАЕ. Ребра РА и РЕ по условию равны единице. Длину ЕА найдем из ∆FAE, применив теорему косинусов:

Задание. В правильной шестиугольной пирам-е боковые ребра имеют длину 2, а ребра в основании равны 1. Вычислите угол между плос-тями РFA и PDE:

Решение. Сначала надо найти прямую, по которой эти две грани пересекаются. Мы видим одну их общую точку – Р. Продолжим ребра FA и ED до тех пор, пока они не пересекутся в некоторой точке К. Эта точка K также будет общей для плос-тей, проходящих через грани PFA и РЕD. Значит, они пересекаются по прямой РК:

Найдем углы в ∆КЕF, помня при этом, что все в шестиугольнике АВСDEF составляют по 120°:

Получили, что все углы в ∆КЕF составляют по 60°, то есть он равносторонний, и поэтому стороны KE и KF одинаковы. Но также одинаковы и грани FA и DE. Отсюда получаем и равенство отрезков АК и DK:

Теперь сравним ∆АРК и ∆KPD. КР – их общая сторона, АР = РD как боковые ребра правильной пирам-ы, и АК = DK. Получается, что эти треугольники равны.

Далее в ∆АРК опустим высоту АН. Из равенства ∆АРК и ∆KPD вытекает, что и HD будет высотой в ∆PHD, ведь в равных треугольниках высоты должны делить равные стороны в одном и том же отношении. Тогда по определению двугранного угла ∠AHD и будет искомым углом между гранями, ведь KP – линия их пересечения, АН⊥KP и DH⊥KP.

∆AKP – равнобедренный, ведь отрезки АК и АР оказались одинаковыми. Значит, АН не только высота, но и медиана. Поэтому

Отрезок AD окажется диаметром окружности, описанной около шестиугольника. Мы знаем, что радиус такой окружности равен длине стороны шестиугольника, то есть единице. Тогда диаметр будет вдвое больше:

Сегодня мы познакомились с ещё одним видом многогранника –пирамидой. Они нередко встречаются в задачах ЕГЭ, посвященных стереометрии. Особо часто используются правильные пирамиды, поэтому важно помнить их основные свойства.