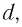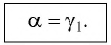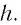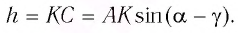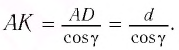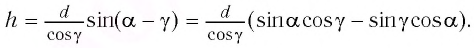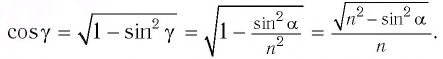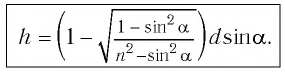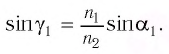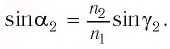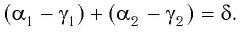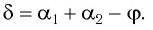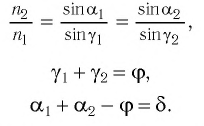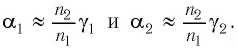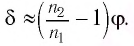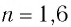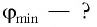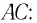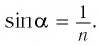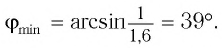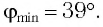Как найти угол между гранями пластинки - Сайт, где вы сможете решить свои вопросы

Максимум излучения будет при 2 m, где m = 0, 1, 2, …. Тогда

Рис.2	2 m 2 d cos ,



	cos (2 m )		(m		).
	2 d	d
				2

б) Условие минимума в направлении φ = 0 имеет вид

2 2 d cos0 2 m .

2 d 2 m .	(1)

В направлении φ = π разность хода	меняет знак, и условие максимума
имеет вид
2 d	2 m ,

2 d 2 m .	(2)

Из уравнений (1) и (2) найдем		и d m	1 .
	2		4

5.2.2. Имеются 2 когерентных источника излучения S1 и S2, расстояние между

которыми d, а длина волны излучения . На экране, расположенном параллельно

линии источников излучения и на большом удалении L наблюдается интерференционная картина (рис. 3). Определить: а) условие, при котором в точке Х будет наблюдаться максимум интерференции; б) ширину интерференционной полосы.

Решение. Запишем уравнения колебаний от источников в точке Х:

							E1 E0 cos( t kL1 ) .
							E	2	E	0	cos( t kL )
													2
Амплитуда результирующего колебания будет
E E1 E2	E0 cos( t kL1 ) cos( t kL2 )
									L L				L	L
	2E	0	cos k	2		1		cos t	k	1	2	.
2					2

Максимальная амплитуда будет при	cos(k	L2	L1	) 1	или	k	L2 L1	= πm,
		2
где m = 0, 1, 2, … Отсюда										2

	2		L2 L1	m,				L L m .

	2										2			1

В точках экрана, до которых разность хода волн от источников равна целому числу длин волны, будет наблюдаться максимум освещенности. В

точке О разность хода 0.		Следовательно, здесь будет интерференционный
максимум. Следующий максимум будет в точке Х, для	которой 1 .
Ширина интерференционной полосы	Х будет равна отрезку ОХ.
Проведем прямую S1M параллельно оси. Из	S1MX L12	L2 ( X d )2
								2
проведем прямую S2N также параллельно оси. Из	S2NX L22	L2 ( X d )2 .
Разность								2

L2	L2	(L L )(L L ) 2L(L L)	2L 2 Xd.
2	1	2	1	2	1	2	L
		2L 2 Xd.	X	.

							d

			X
S1	L1
		M
	L2
d	L	O
		N
S2

	Рис.3
Из рис. 3	видно, что	X	tg , отсюда
		L

угловой размер ширины интерференционной полосы или угловой размер интерференционного максимума d .

5.2.3. Направление распространения	двух плоских волн одной и той же длины
составляют угол φ/2 с нормалью к	плоскости экрана, на котором наблюдаются
интерференционные полосы (рис.4). Показать, что при малых φ расстояние х между
соседними интерференционными полосами х ≈ /φ.

Решение. Запишем уравнение волн
		E1 E0 cos( t k1x r)	,
где		E2	E0	cos( t k2 x r)
		2
k	k sin	sin
		1
	1x	1			.
k		k sin	2	sin

2 x		2
	1					Рис.4
Суммарное колебание

E E1 E2 E0 [cos( t k1x r) cos( t k2 x r)] 2E0 cos(k2 x k1x r) cos( t k2 x r). 2

Максимум результирующего колебания будет при k2 x 2 k1x r m , или

		2						2			r	m ,
				sin 2			sin 1
	2

2		r	(sin		sin	)		(		) m ,

2				2			1		2	1
			r[	( )] m ,	r m .
				2				2

Следующий соседний максимум будет на экране в точке, отстоящей от первоначальной на х. Здесь условие максимума будет иметь вид

r1 (m 1) .

Вычитая из этого уравнения предыдущее, получим

5.2.4. Найти число полос интерференции N, получающихся в установке с бипризмой Френеля. Показатель преломления бипризмы n, преломляющий угол α, длина волны

излучения , расстояние от источника до бипризмы равно а, а расстояние от

бипризмы до экрана равно b.

S
1 d/ 2	a	b
S


S2		L

Рис.5

Решение. Обозначим на чертеже ход лучей и исходные данные (рис.5). Преломляющий угол призмы α, показатель преломления n и угол наименьшего отклонения связаны соотношением

		1
	sin	2	( )
n				,
	sin

				2

которое при малых α переходит в примерное равенство

n ,

отсюда угол отклонения

(n 1) .

По углу отклонения рассчитаем расстояние d между мнимыми

источниками S1 и S2:

d 2atg 2a .

Аналогично найдем ширину интерференционной картины

2L 2b .

Ширина интерференционной полосы

			x (a b) (a b) .
			d	2a
Полное число интерференционных полос N
N	2L		2b 2a	4ab 2	4ab 2 (n 1)2 .
x	(a b)
		(a b)		(a b)

5.2.5. Квазимонохроматический источник света с длиной волны характеризуется

разбросом длин волн . Какому условию должна удовлетворять разность хода

между лучами для наблюдения интерференционной картины?

Решение. Условие наблюдения интерференции – разность хода меньше длины когерентности.

Lêîã .

Длину когерентности можно определить так:

Lêîã c têîã ,

;

êîã

Используемое условие примет вид

2 .

5.2.6. Квазимонохроматический источник света с длиной волны имеет поперечный

размер D. Оценить поперечные размеры области в окрестности точки наблюдения Р, находящейся на расстоянии а от источника, в пределах которой световое поле сохраняет когерентность.

S1		S ‘
	L

S0	a
	1	x

		2
		S”
	‘
		Рис.6

Решение. Пусть узкий источник S0 освещает когерентно две точки S‘ и S”, расположенные симметрично точке Р и находящиеся на расстоянии d друг от друга. В этом случае, если рассматривать S‘ и S” как вторичные источники излучения на экране, перпендикулярном линии S0P и удаленном от Р на расстоянии L, возникает интерференционная картина с шириной интерференционной полосы Х:

X dL .

Угловой размер полуширины интерференционной полосы составит

1 X L . 2 L 2d

Сместим источник S0 в положение S1 на угол α, сместится и интерференционная картина. Если отрезок S0S1 будет представлять собой непрерывный источник света размера D, то каждый участок этого источника создаст свою интерференционную картину. Освещенность экрана станет равномерной при условии, что смещение максимумов в интерференции, возникающих от осевой части излучателя S0 и от края излучателя S1 составит ½ Х. В этом случае про точки S‘ и S” можно сказать, что они перестали быть когерентными. Исходя из этого условие когерентности S‘ и S” можно представить в виде

α < ,

где α – угловой радиус источника излучения. 2Da . Из α < следует

2Da 12 d или d D .

5.2.7. В интерференционной схеме с зеркалами Френеля угол между зеркалами α = 12′, расстояние от линии пересечения зеркал до узкой щели S и экрана Э равны соответственно r = 10,0 см и b = 130 см. Длина волны света = 0,55 мкм. Определить:

а) ширину интерференционных полос на экране и число возможных максимумов; б) сдвиг интерференционной картины на экране при смещении щели δl = 1,0 мм по дуге радиуса r с центром в точке О; в) при какой ширине hmax интерференционные полосы на экране пропадут?

Решение. На рис.7 показан ход лучей в		M2‘ M1		S
установке с бизеркалами Френеля. S1 и S2	S1		r	x2
– это изображения источника света S в			b
	d	O
	S2
	S1	M2	x ‘
			1
				Э

2r sin

d 2r sin .

зеркалах. С другой стороны, мы их рассматриваем как когерентные источники, создающие интерференционную картину.

А) Выразим расстояние между S1 и S2 через r
и угол α.	Рис.7
Из	S1ОS2
	d 2r sin ,
из	S1ОS следует
	S1OM 2 ‘ SOM1 ,

из S2ОS

SOM1 S1OM 2 ‘ 2 .

Отсюда α = φ и Если обозначить расстояние от источников S1 и S2 до экрана через L, то получим L r cos b .

Ширина интерференционной полосы Х

X L (b r cos ) d

при условии, что мал.

X (b r) . 2r

На рис.7 отрезок х1х2 на экране есть ширина интерференционного поля. Число интерференционных полос N

N x1 x2 .

Выразим х1х2 через α и b:

x1 x2 2btg 2bsin 2b ,

тогда	2b 2r		4br 2
N		.
(b r)	(b r)

Число максимумов n с учетом нулевого	n N 1.

б) Точки S, S1 и S2 удалены от O на одинаковое расстояние, следовательно, они лежат на окружности радиуса r. При повороте S вокруг О на расстоянии δl по окружности смещение по углу составит δl/r. На такой же угол сместятся и точки S1 и S2, а следовательно, и интерференционная картина. Линейное смещение картины по экрану составит

x b l / r.

в) В случае, если источник не точечный, а имеет размер h, на экране будут создаваться интерференционные картины каждым участком δх источника, и эти картины будут смещены относительно картины, полученной от центра источника, на величину

x bdh / r.

Отсюда найдем максимальный размер hmax, при котором исчезает интерференционная картина:

b	1 h / r	1		(b r)	,
	2 max	2		2r

h	(b r)	(1 r / b) .
max	4 b	4

Подставляя данные условия, находим	х = 1,1 мм, h = 9, nmax = 43 мкм.

5.2.8. Плоская монохроматическая волна падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми d = 2,5 мм на экране, расположенном за диафрагмой на L = 100 см образуется интерференционная картина. На какое расстояние и в какую сторону смещаются интерференционные полосы, если одну из щелей перекрыть стеклянной пластиной толщиной h = 10 мкм.

Решение. На рис.8. приведена схема опыта.

В	отсутствие стеклянной	пластинки				X
интерференционный	максимум	будет	S1		L1
наблюдаться в точке О. Отрезки S1O и S2O			M


равны.	Если	рассматривать	d		L2	O
	L
интерференционные	максимумы	выше			N
S2

точки О, например, в точке О1, то можно
заметить, что путь S1O‘ меньше S2O‘. Для			Рис.8

того	чтобы	разность	путей	S1O‘ и	S2O‘

стала равна нулю, необходимо как-то увеличить оптический путь S1O‘, например, перекрыв отверстие S стеклянной пластинкой толщины h.

Добавочная длина пути составит

h(n 1),

где n – показатель преломления стекла.

Таким образом, интерференционная картина смещается в сторону источника, который перекрывается пластинкой. Величина смещения интерференционной картины X OO‘ связана с разностью хода лучей

соотношением		x d	h(n 1). Отсюда	x h(n 1)L	0,01 0,5 1 103	2
L	2,5
			d

мм.

5.2.9. В очень тонкой клиновидной пластинке в отраженном свете при нормальном падении наблюдаются интерференционные полосы. Расстояние между соседними темными полосами х = 5 мм. Зная, что длина световой волны = 5800 Å, а

показатель преломления пластинки n = 1,5, найти угол α между гранями пластинки.

Решение. Интерферировать будут лучи, отраженные от передней и задней поверхностей клина (рис.9). Два соседних интерференционных минимума (темные полосы I и II) отличаются друг от друга тем, что в месте нахождения полосы II оптический путь луча удлинился на величину 2ln и

это удлинение равно длине волны

2ln .

Из рис.9 видно, что l x tg x . Тогда 2 x n .

	5,8 10	4	5	Рис.9
2n x	2 1,5	5 3,87 10
ðàä 8 .

5.2.10. В оптических приборах потери света при прохождении через прибор происходят, главным образом, вследствие отражения света от поверхностей оптических деталей. Для увеличения поверхностной прозрачности стекла его поверхность покрывают тонкой пленкой, показатель преломления которой меньше показателя преломления стекла. Каковы должны быть толщина пленки и ее показатель преломления, чтобы отражательная способность обратилась в ноль?

Решение. Отражательная способность будет иметь минимальное значение в случае, когда световые волны, отраженные от верхней и нижней поверхностей пленки, будут иметь противоположные фазы. Толщина пленки должна быть такой, чтобы разность хода равнялась /2. При нормальном падении света на пленку

2dn 2 .

Оба отраженных луча будут испытывать скачок фазы на π, поэтому разность хода от скачка фаз не зависит. Условие минимума интерференции примет вид

2dn	,	d	.
2
		4n

Можно сказать, что минимальная толщина пленки равна четверти длины волны излучения в вакууме.

Рассмотрим условия на показатель преломления. Отраженного излучения не будет при условии равенства интенсивностей излучения, отраженного от верхней и нижней поверхностей пленки.

При нормальном падении излучения из воздуха на пленку по формулам Френеля коэффициент отражения излучения на верхней поверхности 1 равен

1 1 n 2 .1 n

Коэффициент отражения на нижней поверхности пленки 2 равен

2 n ncò 2 ,

n nñò

где n – показатель преломления пленки, а nст – показатель преломления стекла. Равенство отраженных потоков излучения будет при 1 = 2. Отсюда

			1 n	n ncò ,	n nñò .
II			1 n	n nñò
		Если показатель преломления стекла nст = 1,50,
I
		то показатель преломления пленки n = 1,22.

i	K	n0= 1	5.2.11. На тонкую плоскопараллельную пластинку падает
		параллельный пучок монохроматического света под углом
A	O	C	i с длиной волны . Толщина пластинки d, показатель
d		n

преломления n. Найти условие, при котором отраженный свет будет максимально ослаблен вследствие интерференции.

Решение. Рассмотрим ход падающих, отраженных и преломленных лучей (рис.10). Луч I в точке A частично отражается, частично преломляется.

Преломленный луч в точке В (нижней плоскости пластинки) испытывает

отражение и в точке С выходит из пластинки под углом i. Луч II, падающий

на пластинку в точке С, также отразится под углом i. Таким образом, лучи I и

Рис.10

II будут интерферировать на верхней плоскости пластинки, если

разность хода лучей будет меньше длины когерентности.

Рассчитаем разность хода .

Луч I по сравнению с

лучом

проходит

дополнительно

путь 1,

равный АВ + ВС. Луч II проходит в воздухе дополнительный путь

2, равный

отрезку КС + /2. /2 появляется за счет изменения фазы при отражении от

более плотной среды.

1 2 2AB n KC

Из

AOB: AB

;

AO d tg .

cos

AKC KAC KCA / 2,

KCA i / 2,

следовательно KCA i.

KC AC sin i 2AOsin i 2dtg sin i.

2dn

2d sin sin i

(n sin sin i)

cos

Углы β

связаны

законом

преломления

sin i

отсюда

sin

sin i

sin

. Тогда

2 i

n2 sin

2 i

sin

cos

Выразим cosβ сначала через sinβ, а затем через sini:

cos

1 sin2

1 sin2 i

n2 sin2 i.

Подставим это выражение в

2dn (n2

sin2 i)

sin2

n2 sin2

i n

Условие минимума интерференции примет вид

sin2 i

k ,

sin2 i k ,

где k = 1, 2, 3, … .

5.2.12. Сферическая линза радиуса R = 1 м лежит на плоскопараллельной стеклянной пластинке выпуклой поверхностью. Система освещается монохроматическим

излучением с длиной волны = 500 нм. Найти радиус пятого светлого кольца.

Наблюдение ведется в отраженном свете.

O	R		Решение.	Нарисуем ход лучей	(рис.11). В	точке А,
		лежащей	на верхней грани	пластинки,	падающее

K	rm	B	излучение частично отразится,	а частично пройдет и
A	отразится	от сферической поверхности в точке В.
h
			Отраженный в точке В луч вернется в точку А, где
			произойдет наложение с лучом, отраженным в точке А.
			В случае,	если разность хода лучей меньше длины
			когерентности, будет наблюдаться интерференционная

	Рис.11	картина в виде концентрических темных и светлых
	колец.

		Найдем радиус m-го светлого кольца rm. Пусть

толщина воздушного зазора в точках, где наблюдается m-ое светлое кольцо, равна d. Из KOВ rm2 R2 (R h)2 2hR. Отсюда 2h rm2 / R. Найдем разность

хода лучей с учетом скачка фазы отраженного луча в точке В:

2h 2 .

Условие интерференционного максимума примет вид

2h m . 2

rm2 / R m 2 .

Отсюда радиус m-го светлого кольца

2		2m 1
rm	R	2	.

Здесь m = 1, 2, 3, … . Условие минимума интерференции приводит к выражению для радиуса m-го темного кольца в виде

rm2 R m.

Подставляя данные условия задачи для 5-го светлого кольца, получим r5 = 1,5

O	мм, для 5-го темного кольца r5 = 1,6 мм. Центр
	интерференционной картины будет темным.

		R1
D
	N	B
M		n
rm	С
K	A

2a n1

5.2.13. На поверхности жидкости с показателем преломления n1 плавает очень тонкая линза с показателем преломления n < n1, геометрические размеры которой показаны на рис.12. Рассчитать, какая картина будет видна в отраженном

монохроматическом свете с длиной волны , если

смотреть на линзу сверху.

Решение. Так как линза образована сферическими поверхностями, интерференционная картина

Рис.12

Источник

Содержание:

Прохождение света через плоскопараллельные пластинки и призмы:

Законы отражения и преломления света широко используются для управления ходом световых пучков. Для отражения света в приборах применяются зеркала и призмы, для преломления — призмы, плоскопараллельные пластинки, линзы.

Зеркала, призмы, пластинки и линзы являются элементами, комбинируя которые, создают различные оптические приборы. Рассмотрим отдельные элементы оптических приборов.

Плоскопараллельная пластинка

Рассмотрим ход луча в плоскопараллельной пластинке. На рисунке 77 показан ход светового луча в плоскопараллельной пластинке толщиной

Согласно закону преломления на первой и второй границах раздела для луча, падающего под углом на первую границу, имеем:

Здесь — угол преломления на первой границе, — угол падения луча на вторую границу, — угол преломления на второй границе, — абсолютный показатель преломления вещества пластинки.

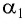
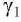
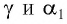
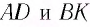
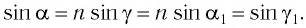
Накрест лежащие углы при параллельных прямых (перпендикулярах к первой и второй параллельным границам) равны, т. е. Следовательно, Откуда следует, что

Таким образом, луч света, проходя через плоскопараллельную пластинку, с обеих сторон которой находится одна и та же среда, смещается параллельно своему начальному направлению на некоторое расстояние

Соответственно, все предметы, если смотреть на них сквозь прозрачную плоскопараллельную пластинку под углом, не равным нулю, будут также казаться смещенными.

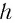
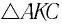
Найдем, от каких параметров пластинки зависит смещение луча. Из 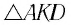следует, что

Из имеем:

Отсюда:

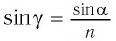
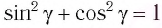
С учетом закона преломления и тригонометрического тождества находим:

Расстояние между направлениями входящего и выходящего лучей можно определить из соотношения

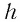
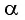
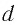
Как видно из соотношения (2), смещение луча при данном угле падения зависит от толщины пластинки и ее показателя преломления

Трехгранная призма

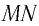
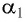
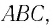
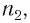
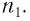
Рассмотрим ход луча в трехгранной призме. Пусть световой луч падает под углом на боковую грань трехгранной призмы сечение которой показано на рисунке 78. Призма, изготовленная из вещества с абсолютным показателем преломления находится в среде с абсолютным показателем преломления Угол при вершине называется преломляющим углом призмы. Грани призмы, образующие преломляющий угол называются преломляющими. Грань, лежащая напротив преломляющего угла, называется основанием призмы.

Пусть луч лежат в одной плоскости — плоскости листа книги. Из закона преломления света находим угол преломления

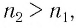
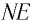
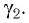
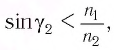
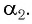
Если показатель призмы то преломленный луч падает на вторую боковую грань призмы под углом Полного отражения на второй преломляющей грани не происходит при условии и луч выходит из призмы под углом Его находим из закона преломления:

Отклонение от начального направления луча вследствие преломлений на гранях призмы определяется углом (см. рис. 78). Угол между направлениями входящего и выходящего лучей называется углом отклонения.

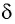
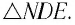
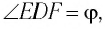
Рассмотрим С учетом того, что по теореме о внешнем угле треугольника находим:

Применим эту же теорему к

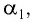
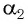
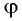
Из формул (5) и (6) определим связь угла падения угла преломления с преломляющим углом призмы и углом отклонения выходящего луча от начального направления:

В результате получим систему уравнений (3), (4), (5), (7):

Система уравнений (8) позволяет решить задачу на прохождение луча света через трехгранную призму без полного отражения на ее гранях.

Заказать решение задач по физике

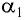
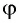
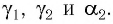
Если угол падения на грань призмы и преломляющий угол призмы малы, то малыми будут и углы Поэтому в законах преломления (3) и (4) отношение синусов можно заменить отношением углов, выраженных в радианах, т. е.:

Подставляя полученные выражения для 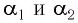в соотношение (7), находим:

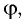
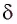
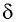
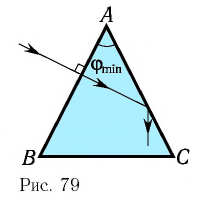
Из соотношения (9) следует, что, во-первых: чем больше преломляющий угол тем больше угол отклонения лучей призмой; во-вторых, угол отклонения лучей увеличивается с ростом абсолютного показателя преломления вещества призмы. Как видно из рисунка 78, луч света, проходя через трехгранную призму, отклоняется к ее утолщенной части, если абсолютный показатель преломления вещества призмы больше абсолютного показателя преломления окружающей среды

Пример решения задачи

Определите наименьший преломляющий угол 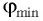стеклянной призмы, находящейся в воздухе, при котором луч, падающий нормально на грань призмы, не выйдет через ее вторую боковую грань (рис. 79). Показатель преломления стекла призмы

Дано:

Решение:

Запишем условие полного отражения на боковой грани

Вследствие того, что 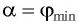как углы с взаимно перпендикулярными сторонами:

Ответ:

Поляризация света
Линзы в физике
Глаз как оптическая система
Звук в физике и его характеристики
Электромагнитная природа света
Интерференция света
Дифракция света
Принцип Гюйгенса — Френеля

Источник

Геометрическая оптика: пластинки

В этой статье решаем задачи с пластинками – средние по сложности. Будем применять закон преломления Снеллиуса, а также геометрические знания.

Задача 1. Прямоугольная стеклянная пластинка толщиной 4 см имеет показатель преломления 1,6. На ее поверхность падает луч света под углом . Определите, на сколько сместится луч после выхода из пластинки в воздух.

К задаче 1

По закону Снеллиуса

Из рисунка

Ответ: 2,4 см.

Задача 2.

Луч света падает под углом на плоскопараллельную стеклянную пластинку и выходит из нее параллельно первоначальному лучу. Показатель преломления стекла равен 1,5. Какова толщина пластинки, если расстояние между лучами равно 1,94 см?

К задаче 2

По закону Снеллиуса

Из рисунка

Откуда

По теореме Пифагора

Ответ: 10 см.

Задача 3.

Узкий параллельный пучок света падает на плоскопараллельную стеклянную пластинку под углом , синус которого равен 0,8. Вышедший из пластинки пучок оказался смещенным относительно продолжения падающего пучка на расстояние 2 см. Какова толщина пластинки, если показатель преломления стекла равен 1,7?

Задача аналогична предыдущей, только данные чуть-чуть иные, поэтому просто подставим их в готовую формулу:

По закону Снеллиуса

Из рисунка

Откуда

По теореме Пифагора

Ответ: 4,73 см.

Задача 4.

Имеются две плоскопараллельные пластинки толщиной 16 и 24 мм, сложенные вплотную. Первая сделана из кронгласа с показателем преломления 1,5, а вторая – из флинтгласа с показателем преломления 1,8. На поверхность одной из них падает луч света под углом . Определите, на сколько сместится этот луч после выхода из пластинок в воздух. Зависит ли полученный результат от того, в какой последовательности свет проходит пластинки?

Порядок установки пластинок неважен: это показано на рисунке.

К задаче 4

По закону Снеллиуса

Тогда

Ответ: 16,38 мм.

Задача 5. На плоскопараллельную стеклянную пластинку толщиной 1 см падает луч света под углом . Показатель преломления стекла равен 1,73. Часть света отражается, а часть, преломляясь, проходит в стекло, отражается от нижней поверхности пластинки и, преломляясь вторично, выходит в воздух параллельно первому отраженному лучу. Найдите расстояние между отраженными лучами.

К задаче 5

В треугольнике угол равен . В этом треугольнике нам нужно найти , а его гипотенуза:

По закону Снеллиуса

Ответ: см.

Задача 6. Плоскопараллельная пластинка толщиной 5 см посеребрена с нижней стороны. Луч падает на верхнюю поверхность пластинки под углом , частично отражается, а часть света проходит в пластинку, отражается от нижней ее поверхности и, преломляясь вторично, выходит в воздух параллельно первому отраженному лучу. Определите показатель преломления материала пластинки, если расстояние между двумя отраженными лучами 2,5 см.

К задаче 6

В треугольнике угол равен . В этом треугольнике нам известен катет см, что позволяет нам найти гипотенузу:

По закону Снеллиуса

Ответ:

Источник

В курсе школьной физики изучаются две преломляющие системы:

плоскопараллельная пластинка
призма

Плоскопараллельной пластинкой называется оптически прозрачная система (параллелепипед с двумя параллельными гранями). Расстояние между этими двумя плоскостями достаточно мало (рис. 1).

Рис. 1. Плоскопараллельная пластинка

Пусть дана плоскопараллельная пластинка шириной и точечный источник $displaystyle {{n}_{2}}$ , из материала с показателем преломления $displaystyle {{n}_{1}}$ . Данная плоскопараллельная пластинка помещена в среду с показателем преломления $displaystyle {{alpha }_{1}}$ . От источника под углом $displaystyle {{alpha }_{1}}$ к вертикали падает луч света (на границу раздела сред 1/2). В точке А происходит преломление луча. Далее луч, распространяющийся внутри пластины, падает на вторую границу раздела (в данном случае, 2/1). В точке В также происходит преломление, и луч выходит из системы. Проанализируем ход луча:

преломление в точке А можно описать законом Снеллиуса:

$displaystyle {{n}_{1}}sin {{alpha }_{1}}={{n}_{2}}sin {{alpha }_{2}}$ (1)

за счёт параллельных граней пластинки, в точку В луч падает под тем же углом $displaystyle {{alpha }_{2}}$ (накрест лежащие углы)
преломление в точке В также можно описать законом Снеллиуса:

$displaystyle {{n}_{2}}sin {{alpha }_{2}}={{n}_{1}}sin {{alpha }_{3}}$ (2)

Т.е. анализ прохождения луча основывается на законах преломления. Избавимся в соотношениях (1) и (2) от параметров второй среды (пластинки), тогда:

$displaystyle {{n}_{1}}sin {{alpha }_{1}}={{n}_{1}}sin {{alpha }_{3}}$ (3)

Или, сократив:

$displaystyle sin {{alpha }_{1}}=sin {{alpha }_{3}}$ (4)

Из соотношения (4) можно сделать вывод, что $displaystyle {{alpha }_{1}}={{alpha }_{3}}$ , что говорит о том, что луч, проходя плоскопараллельную пластинку, выходит из неё под тем же углом (угол падения на пластинку равен углу выхода из пластинки). Таким образом, плоскопараллельная пластинка не меняет направления распространения луча, а смещает его. Для характеристики смещения луча относительно первоначального направления — displaystyle x (рис. 2).

Призмой называется оптически прозрачная система в форме геометрического тела — призмы, которая имеет плоские полированные грани, через которые входит и выходит свет.

Рис. 2. Призма

Одним из параметров призмы являются преломляющий угол призмы () — угол между гранями на призмы, на одну из которых луч света падает, с другой грани уходит. В основном, задачи на призму касаются угла отклонения луча ( displaystyle alpha ), т.е. угла между падающим лучом (его продолжением) и лучом, выходящим из призмы (его продолжением). Тогда для призмы выведено соотношение:

displaystyle alpha =i+r-varphi (5)

Вывод: для оптических систем достаточно прорисовать ход лучей через систему (исходя из законов преломления). А далее, с помощью рисунка, найти необходимые в задаче элементы чаще всего с помощью закона Снеллиуса и геометрических соотношений.

Источник

Условие

В тонкой клинообразной пластинке в отраженном свете при нормальном падении лучей с длиной волны Л=450 нм наблюдаются темные интерференционные полосы, расстояние между которыми 1,5 мм. Найти угол в между гранями пластинки, если ее показатель преломления 1,5.

физика ВУЗ
6983

Решение

★

tga = kλ/2nL
a = 10^(-4) рад

Написать комментарий

Источник

Плоскопараллельная пластинка

Трехгранная призма

Пример решения задачи

Геометрическая оптика: пластинки

Условие

Решение

Написать комментарий

Вам также может понравиться

Как найти на матросской тишине

Как найти айфон по датчику

Как исправить дефект краски

Добавить комментарий Отменить ответ