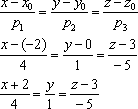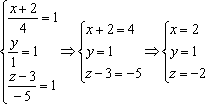Как найти угол между каноническими прямыми

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

и

где q₁=(m₁, p₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

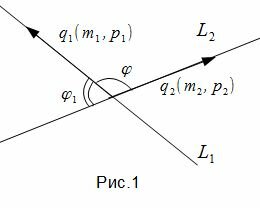
Пример 1. Определить угол между прямыми

и

Решение. Прямая (1.5) имеет направляющий вектор q₁=(m₁, p₁)=(3, 4), а прямая (1.6) − q₂=(m₂, p₂)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m₁, p₁, m₂, p₂ в (1.4):

Упростим и решим:

Найдем угол φ

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Ответ.

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

и

Решение. Прямая (1.10) имеет направляющий вектор q₁=(m₁, p₁)=(3, 3), а прямая (1.11) − q₂=(m₂, p₂)=(−2, −2). Тогда

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

и

Решение. Прямая (1.14) имеет направляющий вектор q₁=(m₁, p₁)=(3, 1), а прямая (1.15) − q₂=(m₂, p₂)=(−2, 6). Тогда

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

и

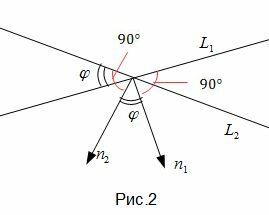
Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

где |n₁| и |n₂| модули нормальных векторов n₁ и n₂ соответственно, φ -угол между векторами n₁ и n₂.

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

и

Решение. Прямая (1.21) имеет нормальный вектор n₁=(A₁, B₁)=(5, −2), а прямая (1.22) − n₂=(A₂, B₂)=(1, 3). Задача определения угла между прямыми L₁ и L₂ сводится к определению угла между векторами n₁ и n₂. Из определения скалярного произведения векторов имеем: (n₁,n₂)=|n₁||n₂|cosφ. Тогда

Подставляя значения A₁, B₁, A₂, B₂ в (1.23), получим:

Упростим и решим:

Найдем угол φ:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

и

Решение. Прямая (1.26) имеет нормальный вектор n₁=(A₁, B₁)=(4, 2), а прямая (1.27) − n₂=(A₂, B₂)=(2, 1). Тогда подставляя значения A₁, B₁, A₂, B₂ в (1.24), получим

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

и

Решение. Прямая (1.29) имеет нормальный вектор n₁=(A₁, B₁)=(4, −1), а прямая (1.30) − n₂=(A₂, B₂)=(2, 8). Тогда подставляя значения A₁, B₁, A₂, B₂ в (28), получим

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

и

где q₁=(m₁, p₁, l₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂, l₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

и

Решение. Прямая (2.5) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 1, 3), а прямая (2.6) − q₂=(m₂, p₂, l₂)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.4):

Упростим и решим:

Найдем угол φ

Ответ.

Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

и

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 4), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(6, 4, 8). Тогда

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

и

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 2, 0), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(2, 4, 0). Подставляя значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.8), получим

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

и

Решение. Прямая (2.16) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 1), а прямая (2.17) − q₂=(m₂, p₂, l₂)=(4, −6, 0). Тогда

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Определение угла между прямыми

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Угол между прямыми через направляющие векторы этих прямых

Угол между прямыми через векторы нормалей этих прямых

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Примеры задач на вычисления угла между прямыми на плоскости

Угол между прямыми в пространстве

Угол между двумя прямыми

Угол φ между
двумя прямыми, заданными общими
уравнениями A₁x
+ B₁y
+ C₁ =
0 и A₂x
+ B₂y
+ C₂ =
0, вычисляется по формуле: 

Угол φ между
двумя прямыми, заданными каноническими
уравнениями (x-x₁)/m₁ =
(y-y₁)/n₁ и
(x-x₂)/m₂ =
(y-y₂)/n₂,
вычисляется по формуле: 

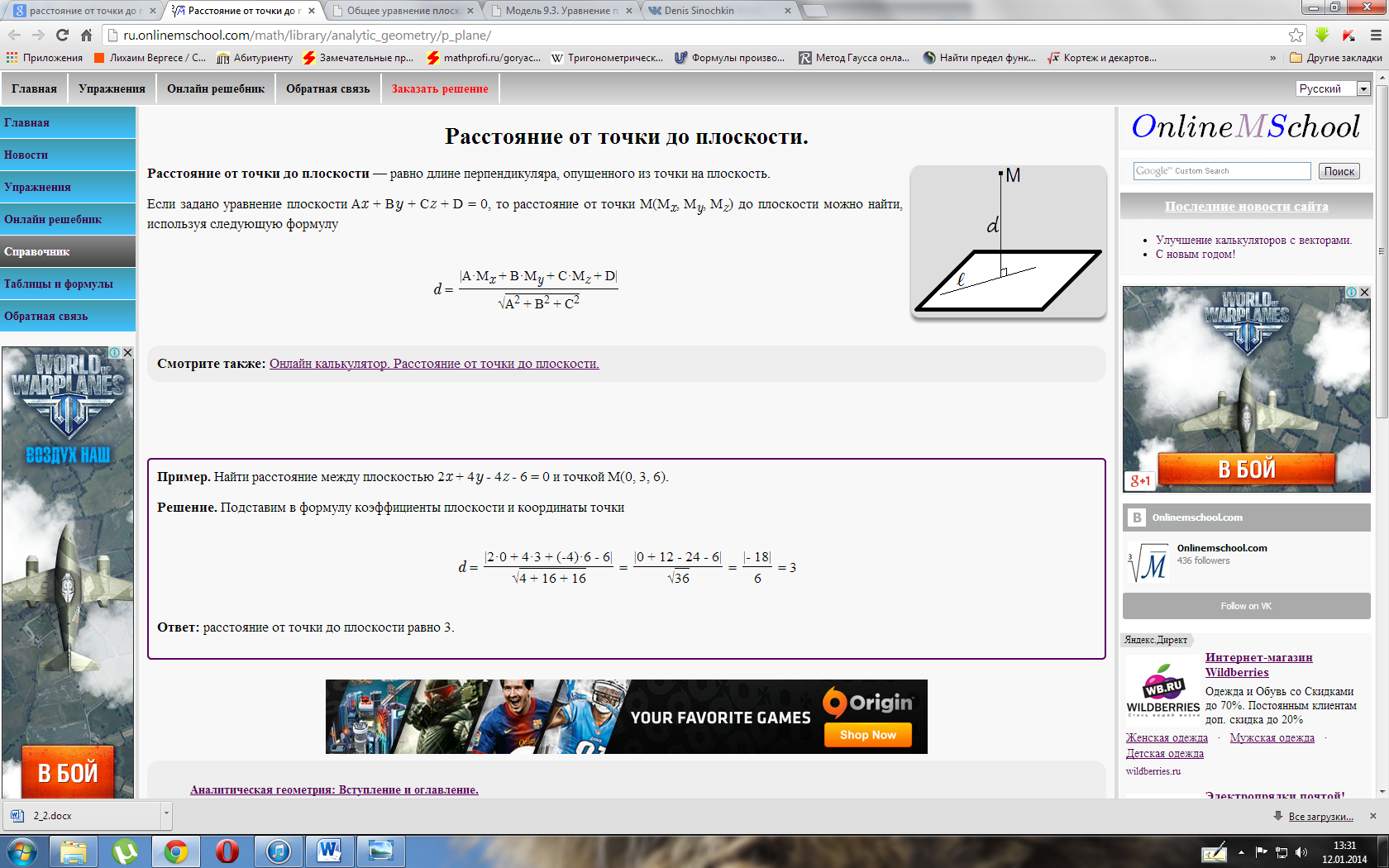
Расстояние от точки до прямой

3,2

Каждую
плоскость в пространстве можно представить
как линейное уравнение, называемое общим
уравнением плоскости

 ,

Частные
случаи.

o     Если
в уравнении (8) ,
то плоскость проходит через начало
координат.

o     При (,)
плоскость параллельна оси(оси,
оси)
соответственно.

o     При (,)  плоскость
параллельна плоскости(плоскости,
плоскости).

Решение:
используем (7)

  ,    

  .

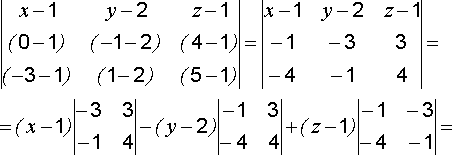
Ответ:
общее уравнение плоскости .

• Пример.

Плоскость
в прямоугольной системе координат Oxyz задана
общим уравнением плоскости .
Запишите координаты всех нормальных
векторов этой плоскости.

Решение.

Нам
известно, что коэффициенты при
переменных x, y и z в общем
уравнении плоскости являются
соответствующими координатами нормального
вектора этой плоскости. Следовательно,
нормальный вектор заданной
плоскостиимеет
координаты.
Множество всех нормальных векторов
можно задать как.

Ответ:

• Пример.

Напишите
уравнение плоскости, если в прямоугольной
системе координат Oxyz в пространстве
она проходит через точку ,
а–
нормальный вектор этой плоскости.

Решение.

Приведем
два решения этой задачи.

Из
условия имеем .
Подставляем эти данные в общее уравнение
плоскости, проходящей через точку:

• Пример.

Напишите
общее уравнение плоскости параллельной
координатной плоскости Oyz и
проходящей через точку .

Решение.

Плоскость,
которая параллельна координатной
плоскости Oyz, может быть задана общим
неполным уравнением плоскости вида .
Так как точкапринадлежит
плоскости по условию, то координаты
этой точки должны удовлетворять уравнению
плоскости,
то есть, должно быть справедливо
равенство.
Отсюда находим.
Таким образом, искомое уравнение имеет
вид.

Решение. Векторное
произведение по определению
10.26 ортогонально
векторам p и q.
Следовательно, оно ортогонально искомой
плоскости и вектор можно
взять в качестве ее нормального вектора.
Найдем координаты вектора n:

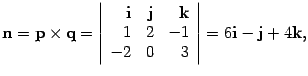
то
есть .
Используя формулу (11.1),
получим

Раскрыв
в этом уравнении скобки, приходим к
окончательному ответу.

Ответ: .
        

• Найти
  единичный нормальный вектор плоскости .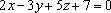

Перепишем
вектор нормали в виде и
найдём его длину:

Согласно
вышесказанному:

Ответ: 

• Построить
  плоскость, проходящую через
  точку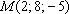  параллельно
  плоскости .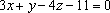

У
параллельных плоскостей один и тот же
вектор нормали. 1) Из уравнения найдём
вектор нормали плоскости:.

2)
Уравнение плоскости составим
по точкеи
вектору нормали:

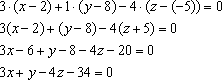
Ответ: 

Векторное
уравнение плоскости в пространстве

Параметрическое
уравнение плоскости в пространстве

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть
в трехмерном пространстве задана
прямоугольная декартова система
координат. Сформулируем следующую
задачу:

Составить
уравнение плоскости, проходящей через
данную точку
M(x0,
 y0,
 z0) перпендикулярно
данному вектору 
n =
{A, B, C}
.

Решение. Пусть P(x, y, z)
— произвольная точка пространства.
Точка P принадлежит
плоскости тогда и только тогда, когда
вектор
MP =
{x − x0, y − y0, z − z0}
ортогонален вектору n =
{A, B, C}
(рис.1).

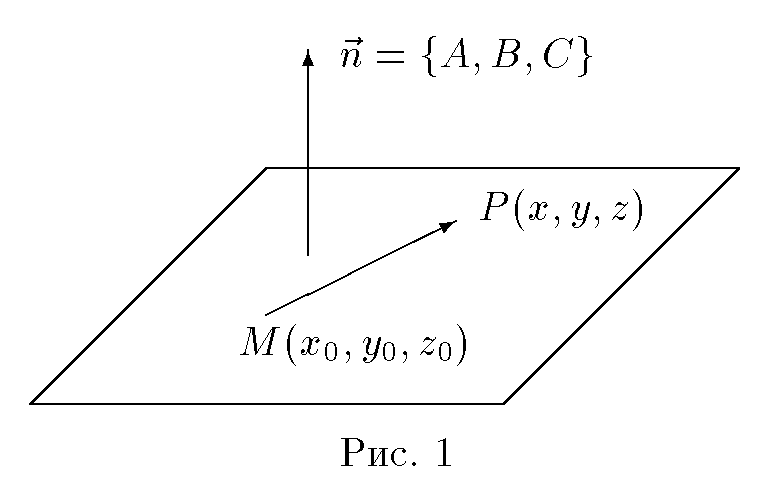
Написав
условие ортогональности этих векторов
(n, MP)
= 0 в координатной форме, получим:

A(x − x0) + B(y − y0) + C(z − z0) = 0

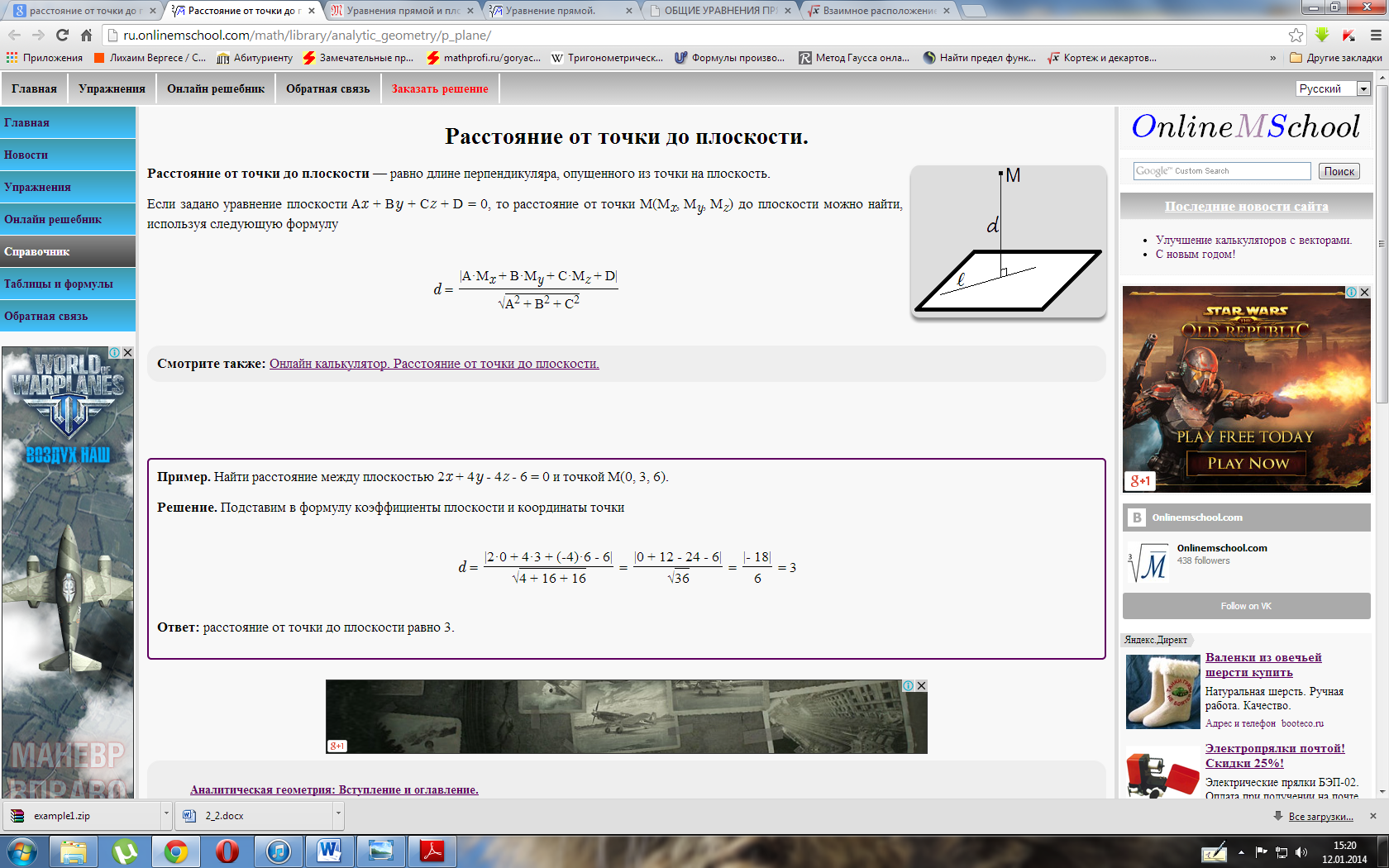
 Уравнение
плоскости по трем точкам 

     В
векторном виде

     В
координатах

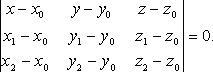
Взаимное
расположение плоскостей в пространстве

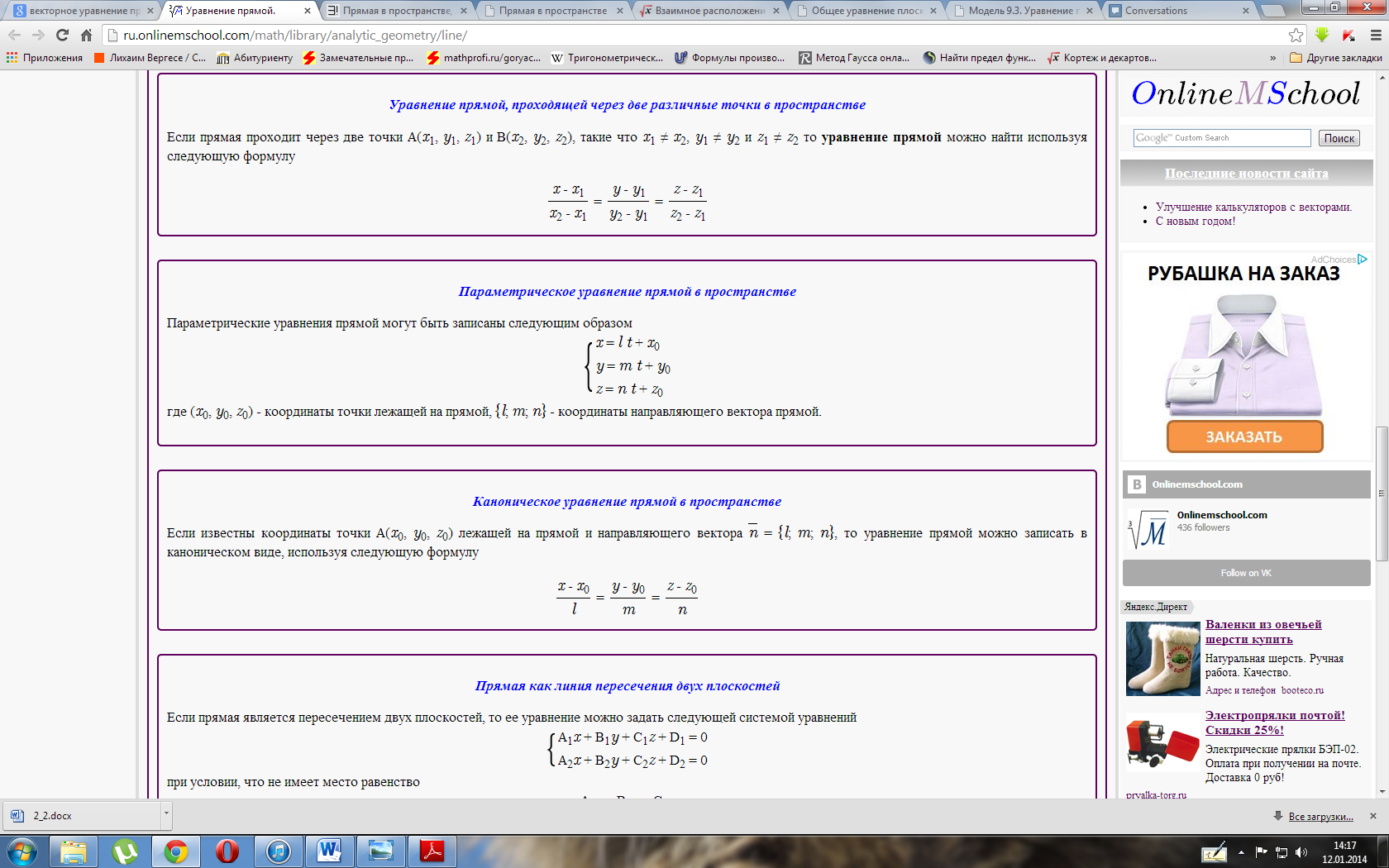
Пусть

 и 

– общие уравнения двух
плоскостей. Тогда:

1)
если ,
то плоскости совпадают;

2)
если ,
то плоскости параллельны;

3) 
если  или ,
то плоскости пересекаются и системауравнений

                       
 (6)

является
уравнениями прямой пересечения данных
плоскостей.

3.3

Составить канонические уравнения прямой по точке  и направляющему вектору  Решение: Канонические уравнения прямой составим по формуле: Ответ:

В ряде задач требуется найти какую-нибудь другую точку , принадлежащую данной прямой. Как это сделать? Берём полученные уравнения  и мысленно «отщипываем», например, левый кусочек: . Теперь этот кусочек приравниваем к любому числу (помним, что ноль уже был), например, к единице: . Так как , то и два других «куска» тоже должны быть равны единице. По сути, нужно решить систему:

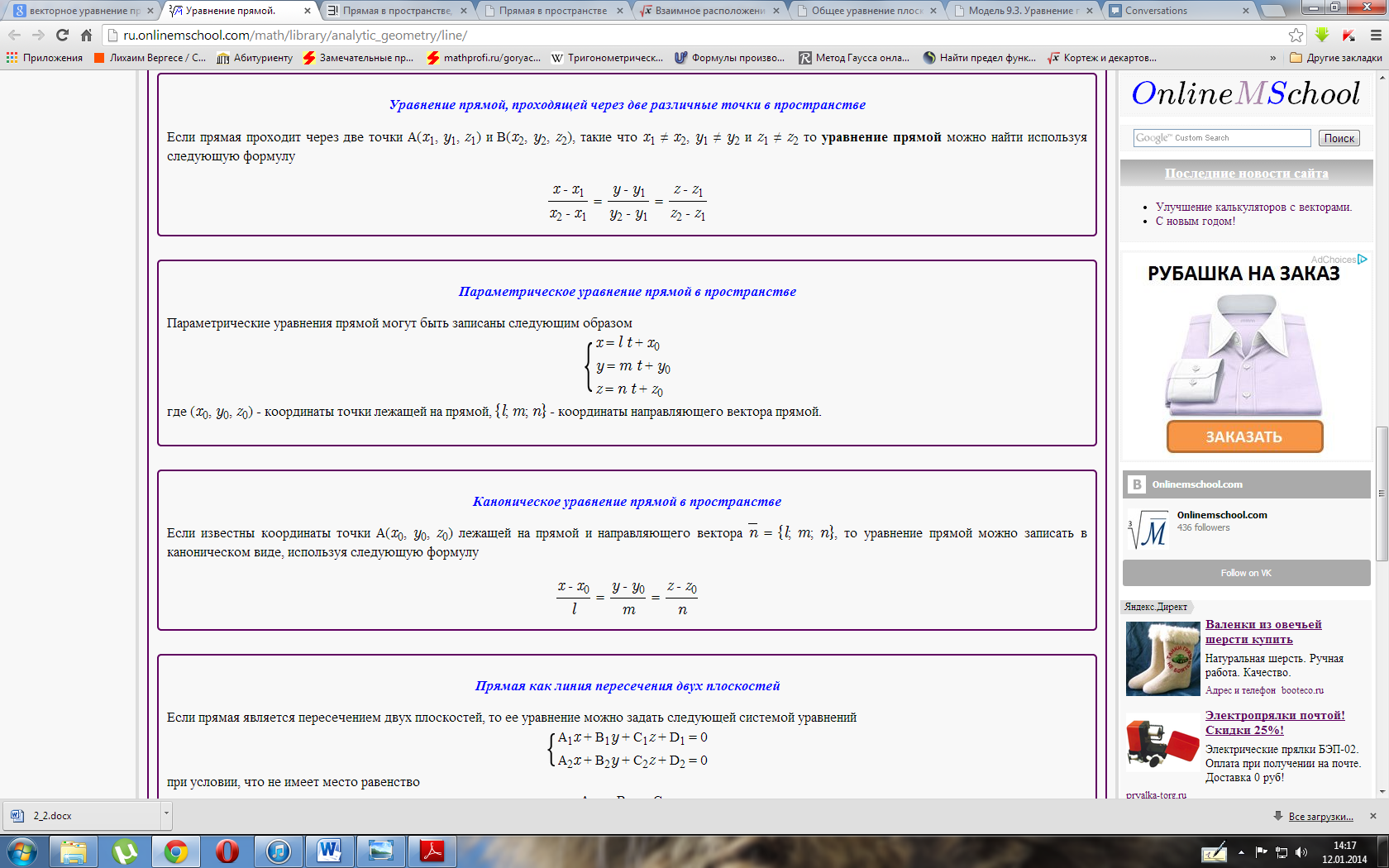
Составить
параметрические уравнения следующих
прямых:

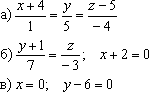
Решение:
Прямые заданы каноническими уравнениями
и на первом этапе следует найти
какую-нибудь точку, принадлежащую
прямой, и её направляющий вектор.

а)
Из уравнений  снимаем
точку и направляющий вектор: .
Точку можно выбрать и другую (как это
сделать – рассказано выше), но лучше
взять самую очевидную. Кстати, во
избежание ошибок, всегда подставляйте
её координаты в уравнения.

Составим
параметрические уравнения данной
прямой:

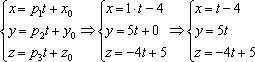
Удобство
параметрических уравнений состоит в
том, что с их помощью очень легко находить
другие точки прямой. Например, найдём
точку ,
координаты которой, скажем, соответствуют
значению параметра :

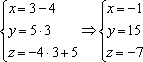
Таким
образом: 

б)
Рассмотрим канонические уравнения .
Выбор точки здесь несложен, но
коварен:  (будьте
внимательны, не перепутайте координаты!!!).
Как вытащить направляющий вектор? Можно
порассуждать, чему параллельна данная
прямая, а можно использовать простой
формальный приём: в пропорции находятся
«игрек» и «зет», поэтому запишем
направляющий вектор ,
а на оставшееся место поставим ноль: .

Составим
параметрические уравнения прямой:

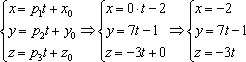
в)
Перепишем уравнения  в
виде ,
то есть «зет» может быть любым. А если
любым, то пусть, например, .
Таким образом, точка  принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях  находятся
«икс» и «игрек», и в направляющем векторе
на данных местах записываем нули: .
На оставшееся место ставим единицу: .
Вместо единицы подойдёт любое число,
кроме нуля.

Запишем
параметрические уравнения прямой:

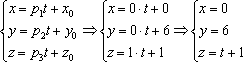
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

,

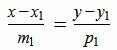(1.1)

,

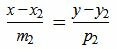(1.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

,

,

(1.3)

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

.

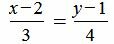(1.5)

.

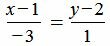(1.6)

.

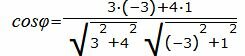Упростим и решим:

.

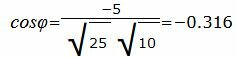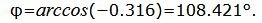
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

.

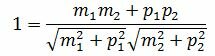(1.7)

Сделаем преобразования с выражением (1.7):

,

,

,

,

.

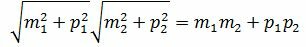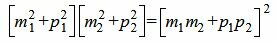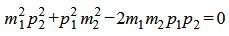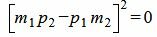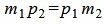(1.8)

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

.

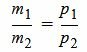(1.9)

Пример 2. Определить, параллельны ли прямые

.

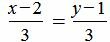(1.10)

.

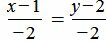(1.11)

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

.

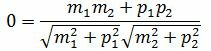(1.12)

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

.

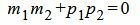(1.13)

Пример 3. Определить, перпендикулярны ли прямые

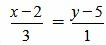(1.14)

.

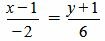(1.15)

.

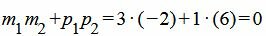(16)

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

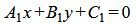(1.17)

.

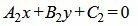(1.18)

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

.

Из определения скалярного произведения двух векторов, имеем:

.

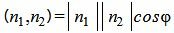(1.19)

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

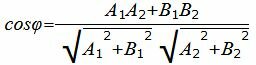(23)

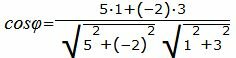
Упростим и решим:

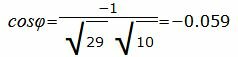
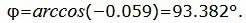
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

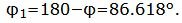
1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

.

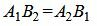(1.24)

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

.

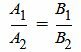(1.25)

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

,

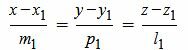(2.1)

,

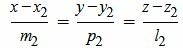(2.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

,

(2.3)

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

.

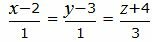(2.5)

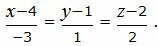(2.6)

.

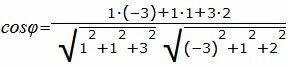Упростим и решим:

.

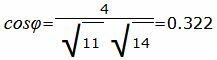Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

m1=αm2, p1=αp2, l1=αl2

(2.7)

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

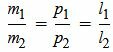(2.8)

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

.

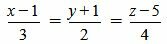(2.9)

.

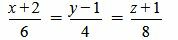(2.10)

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

.

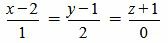(2.11)

.

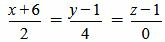(2.12)

.

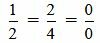(2.13)

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

.

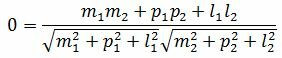(2.15)

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

.

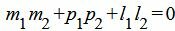(2.16)

Пример 3. Определить, перпендикулярны ли прямые

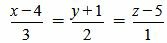(2.17)

.

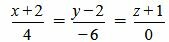(2.18)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Онлайн калькулятор. Угол между прямыми

Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между прямыми.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между прямыми и закрепить пройденный материал.

Найти угол между прямыми

Уравнение 1-ой прямой:

Уравнение 2-ой прямой:

Ввод данных в калькулятор для вычисления угла между прямыми

В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора вычисления угла между прямыми

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Угол между прямыми

Угол между прямыми можно найти, воспользовавшись направляющими векторами этих прямых.

Если вектор a является направляющим вектором первой прямой, а вектор b – направляющий вектор второй прямой то угол между прямыми можно найти, воспользовавшись формулой:

cos φ = | a · b | | a | · | b |

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

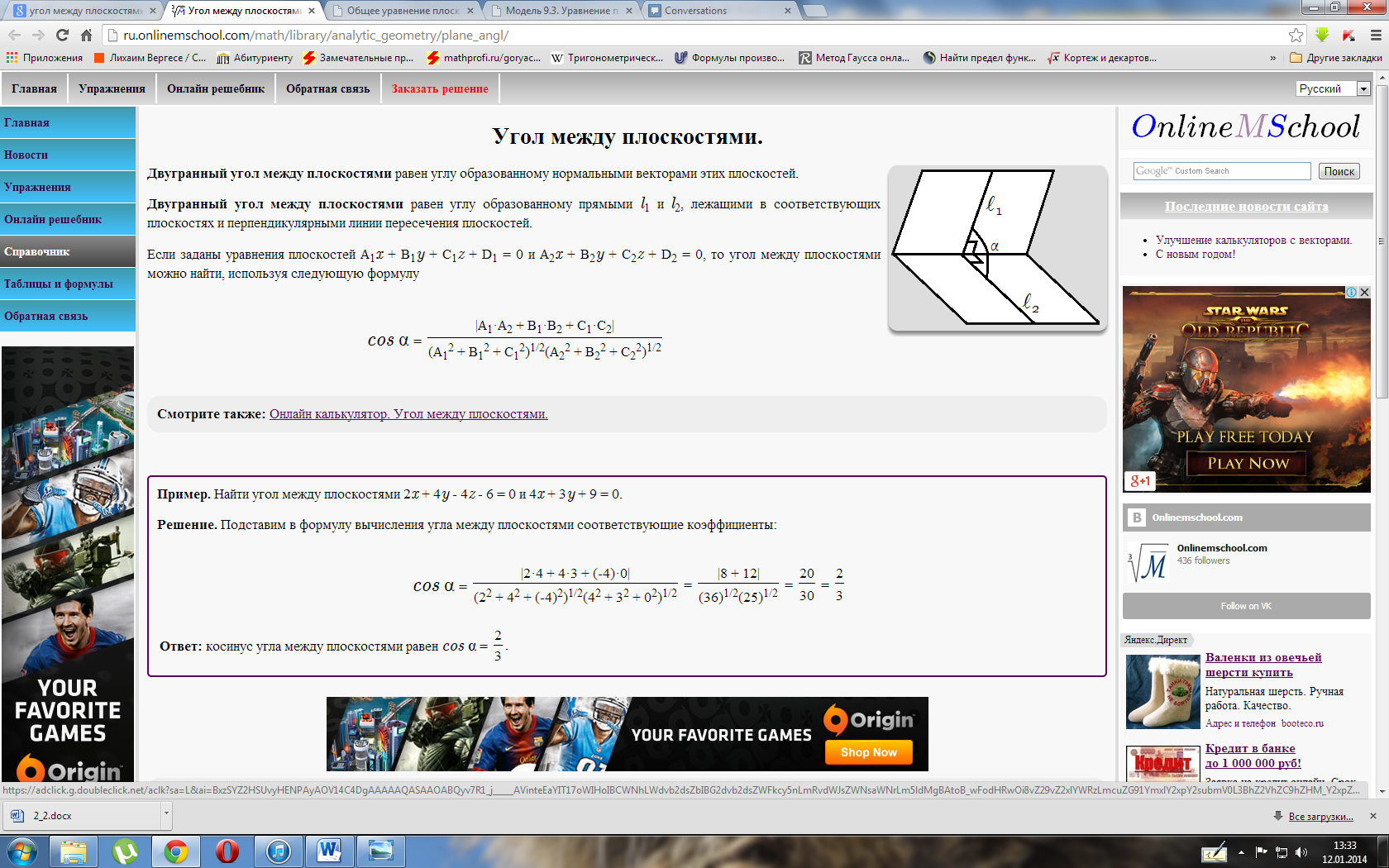
4.2.9. Угол между прямыми. Угол между прямой и плоскостью

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

Косинус угла между ними можно найти по формуле:

(9)

Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:

Условие параллельности прямых,

Условие перпендикулярности прямых.

Угол φ между прямой, заданной каноническими уравнениями

И плоскостью, определяемой общим уравнением

Можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда

Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов N и А:

А Условием перпендикулярности прямой и плоскости – условие параллельности этих векторов:

[spoiler title=”источники:”]

http://ru.onlinemschool.com/math/assistance/cartesian_coordinate/lines_angle/

http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/4-2-9-ugol-mezhdu-priamymi-ugol-mezhdu-priamoi-i-ploskostiu

[/spoiler]

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

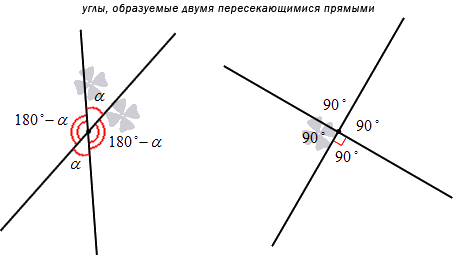
Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).

Взгляните на рисунок:

Перейдем к формулированию основного определения.

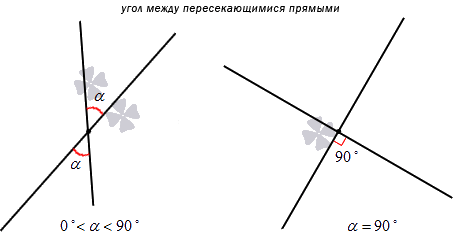
Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.

Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, то угол между ними в любом случае будет равен 90 градусам.

Как найти угол между пересекающимися прямыми на плоскости

Умение находить меру угла между двумя пересекающимися прямыми полезно для решения многих практических задач. Метод решения можно выбрать из нескольких вариантов.

Для начала мы можем взять геометрические методы. Если нам известно что-то о дополнительных углах, то можно связать их с нужным нам углом, используя свойства равных или подобных фигур. Например, если мы знаем стороны треугольника и нужно вычислить угол между прямыми, на которых эти стороны расположены, то для решения нам подойдет теорема косинусов. Если у нас в условии есть прямоугольный треугольник, то для подсчетов нам также пригодится знание синуса, косинуса и тангенса угла.

Координатный метод тоже весьма удобен для решения задач такого типа. Поясним, как правильно его использовать.

У нас есть прямоугольная (декартова) система координат Oxy, в которой заданы две прямые. Обозначим их буквами a и b. Прямые при этом можно описать с помощью каких-либо уравнений. Исходные прямые имеют точку пересечения M. Как определить искомый угол (обозначим его α) между этими прямыми?

Начнем с формулировки основного принципа нахождения угла в заданных условиях.

Нам известно, что с понятием прямой линии тесно связаны такие понятия, как направляющий и нормальный вектор. Если у нас есть уравнение некоторой прямой, из него можно взять координаты этих векторов. Мы можем сделать это сразу для двух пересекающихся прямых.

Угол, образуемый двумя пересекающимися прямыми, можно найти с помощью:

• угла между направляющими векторами;
• ­угла между нормальными векторами;
• угла между нормальным вектором одной прямой и направляющим вектором другой.

Теперь рассмотрим каждый способ отдельно.

1. Допустим, что у нас есть прямая a с направляющим вектором a→=(ax, ay) и прямая b с направляющим вектором b→(bx, by). Теперь отложим два вектора a→ и b→ от точки пересечения. После этого мы увидим, что они будут располагаться каждый на своей прямой. Тогда у нас есть четыре варианта их взаимного расположения. См. иллюстрацию:

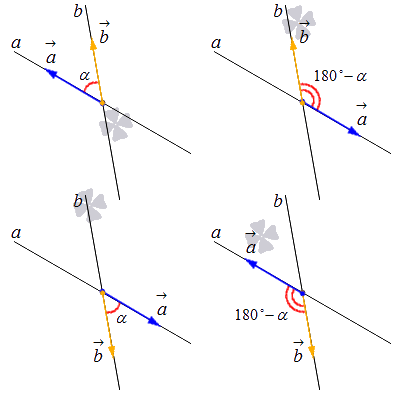
Если угол между двумя векторами не является тупым, то он и будет нужным нам углом между пересекающимися прямыми a и b. Если же он тупой, то искомый угол будет равен углу, смежному с углом a→, b→^. Таким образом, α=a→, b→^ в том случае, если a→, b→^≤90° , и α=180°-a→, b→^, если a→, b→^>90°.

Исходя из того, что косинусы равных углов равны, мы можем переписать получившиеся равенства так: cos α=cos a→, b→^, если a→, b→^≤90°; cos α=cos180°-a→, b→^=-cosa→, b→^, если a→, b→^>90°.

Во втором случае были использованы формулы приведения. Таким образом,

cos αcosa→, b→^, cosa→, b→^≥0-cosa→, b→^, cosa→, b→^<0⇔cos α=cosa→, b→^

Запишем последнюю формулу словами:

Косинус угла, образованного двумя пересекающимися прямыми, будет равен модулю косинуса угла между его направляющими векторами.

Общий вид формулы косинуса угла между двумя векторами a→=(ax, ay) и b→=(bx, by) выглядит так:

cosa→, b→^=a→, b→^a→·b→=ax·bx+ay·byax2+ay2·bx2+by2

Из нее мы можем вывести формулу косинуса угла между двумя заданными прямыми:

cos α=ax·bx+ay·byax2+ay2·bx2+by2=ax·bx+ay·byax2+ay2·bx2+by2

Тогда сам угол можно найти по следующей формуле:

α=arccosax·bx+ay+byax2+ay2·bx2+by2

Здесь a→=(ax, ay) и b→=(bx, by) – это направляющие векторы заданных прямых.

Приведем пример решения задачи.

Мы можем решить подобную задачу с помощью нахождения угла между нормальными векторами. Если у нас есть прямая a с нормальным вектором na→=(nax, nay) и прямая b с нормальным вектором nb→=(nbx, nby), то угол между ними будет равен углу между na→ и nb→ либо углу, который будет смежным с na→, nb→^. Этот способ показан на картинке:

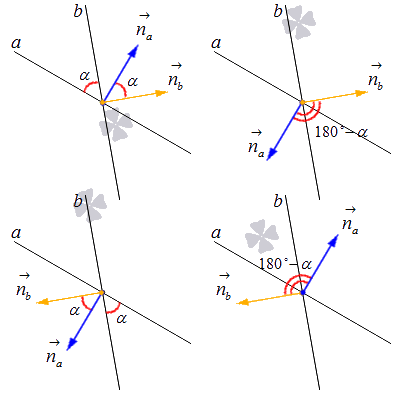
Формулы для вычисления косинуса угла между пересекающимися прямыми и самого этого угла с помощью координат нормальных векторов выглядят так:

cos α=cosna→, nb→^=nax·nbx+nay+nbynax2+nay2·nbx2+nby2α=arccosnax·nbx+nay+nbynax2+nay2·nbx2+nby2

Здесь na→ и nb→ обозначают нормальные векторы двух заданных прямых.

Разберем последний случай – нахождение угла между прямыми, если нам известны координаты направляющего вектора одной прямой и нормального вектора другой.

Допустим, что прямая a имеет направляющий вектор a→=(ax, ay), а прямая b – нормальный вектор nb→=(nbx, nby). Нам надо отложить эти векторы от точки пересечения и рассмотреть все варианты их взаимного расположения. См. на картинке:

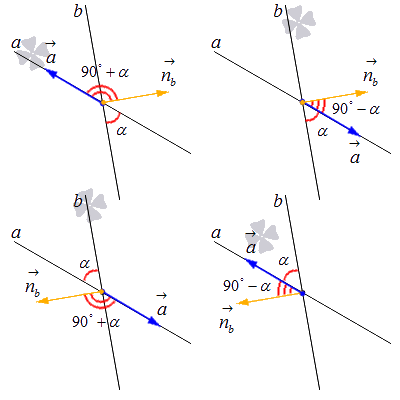
Если величина угла между заданными векторами не более 90 градусов, получается, что он будет дополнять угол между a и b до прямого угла.

a→, nb→^=90°-α в том случае, если a→, nb→^≤90°.

Если он менее 90 градусов, то мы получим следующее:

a→, nb→^>90° , тогда a→, nb→^=90°+α

Используя правило равенства косинусов равных углов, запишем:

cosa→, nb→^=cos(90°-α)=sin α при a→, nb→^≤90°.

cosa→, nb→^=cos90°+α=-sin α при a→, nb→^>90°.

Таким образом,

sin α=cosa→, nb→^, a→, nb→^≤90°-cosa→, nb→^, a→, nb→^>90°⇔sin α=cosa→, nb→^, a→, nb→^>0-cosa→, nb→^, a→, nb→^<0⇔⇔sin α=cosa→, nb→^

Сформулируем вывод.

Чтобы найти синус угла между двумя прямыми, пересекающимися на плоскости, нужно вычислить модуль косинуса угла между направляющим вектором первой прямой и нормальным вектором второй.

Запишем необходимые формулы. Нахождение синуса угла:

sin α=cosa→, nb→^=ax·nbx+ay·nbyax2+ay2·nbx2+nby2

Нахождение самого угла:

 α=arcsin=ax·nbx+ay·nbyax2+ay2·nbx2+nby2

Здесь a→ является направляющим вектором первой прямой, а nb→ – нормальным вектором второй.

Приведем еще один способ нахождения нужного угла с помощью угловых коэффициентов заданных прямых.

У нас есть прямая a, которая задана в прямоугольной системе координат с помощью уравнения y=k1·x+b1, и прямая b, заданная как y=k2·x+b2. Это уравнения прямых с угловым коэффициентом. Чтобы найти угол пересечения, используем формулу:

α=arccosk1·k2+1k12+1·k22+1, гдеk1 и k2 являются угловыми коэффициентами заданных прямых. Для получения этой записи были использованы формулы определения угла через координаты нормальных векторов.

В выводах этого пункта следует отметить, что приведенные здесь формулы нахождения угла не обязательно учить наизусть. Для этого достаточно знать координаты направляющих и/или нормальных векторов заданных прямых и уметь определять их по разным типам уравнений. А вот формулы для вычисления косинуса угла лучше запомнить или записать.

Как вычислить угол между пересекающимися прямыми в пространстве

Вычисление такого угла можно свести к вычислению координат направляющих векторов и определению величины угла, образованного этими векторами. Для таких примеров используются такие же рассуждения, которые мы приводили до этого.

Допустим, что у нас есть прямоугольная система координат, расположенная в трехмерном пространстве. В ней заданы две прямые a и b с точкой пересечения M. Чтобы вычислить координаты направляющих векторов, нам нужно знать уравнения этих прямых. Обозначим направляющие векторы a→=(ax, ay, az) и b→=(bx, by, bz). Для вычисления косинуса угла между ними воспользуемся формулой:

cos α=cosa→, b→^=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2

Для нахождения самого угла нам понадобится эта формула:

α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2