Как найти угол между кривыми калькулятор

Online trigonometry calculator, which helps to find angle between two curves with easy calculation.

Find Angle Between Two Curves

Curve Equation1 (y)

x²+

Curve Equation2 (y)

x²+

Angle between two curves

Calculator
Formula

Online trigonometry calculator, which helps to find angle between two curves with easy calculation.

Code to add this calci to your website

Formula

tan(θ) = (m2-m1)/(1+(m1.m2)) ∀ m2>m1
tan(θ) = (m1-m2)/(1+(m1.m2)) ∀ m1>m2
Where,
m1 = Curve 1 Tangent line slope
m2 = Curve 2 Tangent line slope

How to find angle between two curves?

Related Calculators:

Distance Between Two Points Calculator
Ratio Or Section
Mid Point
Point Slope Form Calculator
Find Acute Angle Between Two Lines And Plane
Date Calculator

Источник

Онлайн калькулятор. Угол между прямыми

Предлагаю вам воспользоваться онлайн калькулятором для вычисления угла между прямыми.

Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между прямыми и закрепить пройденный материал.

Найти угол между прямыми

Уравнение 1-ой прямой:

y = x +

Уравнение 2-ой прямой:

y = x +

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Источник

Данный калькулятор предназначен для вычисления угла между двумя прямыми онлайн.

Две прямые могут иметь три варианта взаимного расположения друг к другу. Они могут совпадать, быть параллельны или же пересекаться. Для определения угла между прямыми наиболее интересным случаем является угол между скрещивающимися (или пересекающимися) прямыми.

Если две прямые имеют одну общую точку, то такие прямые называются пересекающимися. Точка пересечения делит каждую из прямых на два луча. Между лучами пересекающихся прямых образовываются четыре угла (два острых и два тупых). Итак, угол между двумя скрещивающимися прямыми – это наименьший угол (острый), образованный при пересечении этих прямых. Следует отметить, что, если известно значение одного из углов, можно легко найти значения остальных трех углов благодаря свойствам вертикальных и смежных углов.

Для того чтобы найти угол между двумя прямыми с помощью данного калькулятора, необходимо ввести коэффициенты в уравнения прямых и нажать кнопку «Вычислить».

Если прямые заданы следующими уравнениями:

A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0

тогда направляющие векторы этих прямых будут равны:

a₁ = (- B₁ ; A₁) и a₂ = (- B₂ ; A₂)

Воспользуемся формулой скалярного произведения двух векторов:

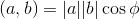
из этой формулы получим:

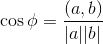
Выразим угол φ :

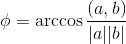
Из последней формулы получим:

Источник

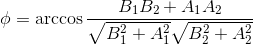
Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

где q₁=(m₁, p₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Решение. Прямая (1.5) имеет направляющий вектор q₁=(m₁, p₁)=(3, 4), а прямая (1.6) − q₂=(m₂, p₂)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m₁, p₁, m₂, p₂ в (1.4):

Упростим и решим:

Найдем угол φ

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Ответ.

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

Решение. Прямая (1.10) имеет направляющий вектор q₁=(m₁, p₁)=(3, 3), а прямая (1.11) − q₂=(m₂, p₂)=(−2, −2). Тогда

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

Решение. Прямая (1.14) имеет направляющий вектор q₁=(m₁, p₁)=(3, 1), а прямая (1.15) − q₂=(m₂, p₂)=(−2, 6). Тогда

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

где |n₁| и |n₂| модули нормальных векторов n₁ и n₂ соответственно, φ -угол между векторами n₁ и n₂.

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

Решение. Прямая (1.21) имеет нормальный вектор n₁=(A₁, B₁)=(5, −2), а прямая (1.22) − n₂=(A₂, B₂)=(1, 3). Задача определения угла между прямыми L₁ и L₂ сводится к определению угла между векторами n₁ и n₂. Из определения скалярного произведения векторов имеем: (n₁,n₂)=|n₁||n₂|cosφ. Тогда

Подставляя значения A₁, B₁, A₂, B₂ в (1.23), получим:

Упростим и решим:

Найдем угол φ:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Решение. Прямая (1.26) имеет нормальный вектор n₁=(A₁, B₁)=(4, 2), а прямая (1.27) − n₂=(A₂, B₂)=(2, 1). Тогда подставляя значения A₁, B₁, A₂, B₂ в (1.24), получим

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Решение. Прямая (1.29) имеет нормальный вектор n₁=(A₁, B₁)=(4, −1), а прямая (1.30) − n₂=(A₂, B₂)=(2, 8). Тогда подставляя значения A₁, B₁, A₂, B₂ в (28), получим

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

где q₁=(m₁, p₁, l₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂, l₂) направляющий вектор прямой L₂.

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Решение. Прямая (2.5) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 1, 3), а прямая (2.6) − q₂=(m₂, p₂, l₂)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.4):

Упростим и решим:

Найдем угол φ

Ответ.

Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 4), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(6, 4, 8). Тогда

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 2, 0), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(2, 4, 0). Подставляя значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.8), получим

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

Пример 3. Определить, перпендикулярны ли прямые

Решение. Прямая (2.16) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 1), а прямая (2.17) − q₂=(m₂, p₂, l₂)=(4, −6, 0). Тогда

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Источник

Калькулятор онлайн.
Вычисление угла между двумя прямыми

Этот калькулятор онлайн вычисляет угол между двумя прямыми заданными в каноническом виде (для трехмерного пространства):

$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} $$

и в виде уравнения прямой с угловым коэффициентом (для двухмерного пространства):

$$ y = kx+b $$

Онлайн калькулятор для вычисления расстояния от точки до плоскости не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода чисел

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )

Уравнения прямой

Линию в пространстве можно рассматривать как пересечение двух поверхностей и определять заданием двух
уравнений. В частности, каждую прямую линию можно рассматривать как пересечение двух плоскостей и соответственно этому определять
заданием двух уравнений первой степени.

Пусть заданы некоторая прямоугольная система координат Oxyz и произвольная прямая L. Обозначим через ( pi_1 ), и ( pi_2 ) две
различные плоскости, пересекающиеся по прямой L, заданные соответственно уравнениями
$$ left{ begin{array}{l} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 end{array} right. tag{1} $$

Два уравнения вида (1) совместно определяют прямую L в том и только в том случае, когда плоскости ( pi_1 ), и ( pi_2 ) не
параллельны и не совпадают друг с другом, т.е. нормальные векторы этих плоскостей ( N_1(A_1;B_1;C_1) ) и ( N_2(A_2;B_2;C_2) ) не
коллинеарны (коэффициенты A₁, B₁, C₁ не пропорциональны коэффициентам A₂, B₂,
C₂).

Уравнения (1) называются общими уравнениями прямой.

Канонические уравнения прямой.

Для решения задач уравнения (1) не всегда удобны, поэтому используют специальный вид уравнений прямой.

Пусть дана какая-нибудь прямая L и ненулевой вектор ( vec{a} ), лежащий на данной прямой или параллельный ей.
Вектор а называется направляющим вектором данной прямой. Выведем уравнения прямой, проходящей через данную точку
( M_0(x_0;y_0;z_0) ) и имеющей данный направляющий вектор ( vec{a}(l;m;n) )

Пусть ( M(x;y;z) ) — произвольная точка. Она лежит на прямой тогда и только тогда, когда вектор
( vec{M_0M}(x-x_0; y-y_0; z-z_0) ) коллинеарен направляющему вектору ( vec{a}(l;m;n) ), т.е. когда координаты
вектора ( vec{M_0M} ) пропорциональны координатам вектора ( vec{a} ):

$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} tag{2} $$

Уравнения (2) и являются искомыми. Они называются каноническими уравнениями прямой.

Для того чтобы составить канонические уравнения (2), если прямая L задана уравнениями (1), необходимо:
1) найти какую-нибудь точку ( M_0(x_0;y_0;z_0) in L ); для этого следует задать числовое значение одной из неизвестных
координат ( x_0, ; y_0, ; z_0 ) и подставить его вместо соответствующей переменной в уравнения (1), после этого две другие
координаты определяются в результате совместного решения уравнений (1);
2) найти направляющий вектор ( vec{a}(l;m;n) ). Так как прямая L определена пересечением плоскостей ( pi_1 ) и ( pi_2 ), то
она перпендикулярна каждому из нормальных векторов ( vec{N_1} ) и ( vec{N_2} ). Поэтому в качестве
вектора ( vec{a} ) можно взять любой вектор, перпендикулярный векторам ( vec{N_1} ) и ( ; vec{N_2} ),
например их векторное произведение ( vec{a}= vec{N_1} times vec{N_2} ). Так как координаты векторов
( vec{N_1} ) и ( vec{N_2} ) известны:
( vec{N_1}(A_1;;B_1;;C_1), ;; vec{N_2}(A_2;;B_2;;C_2) ) , то по теореме найдем координаты вектора ( vec{a} ):

( vec{a} = left{ begin{vmatrix} B_1 & C_1 \ B_2 & C_2 end{vmatrix} ; ; ;
begin{vmatrix} C_1 & A_1 \ C_2 & A_2 end{vmatrix} ; ; ; begin{vmatrix} A_1 & B_1 \ A_2 & B_2 end{vmatrix} right} =
(l; m; n) )

Параметрические уравнения прямой

Иногда прямую полезно задавать не в виде канонических уравнений (2), а иначе. Пусть прямая L задана уравнениями (2). Обозначим
через t каждое из равных отношений. Тогда

$$ frac{x-x_0}{l} = frac{y-y_0}{m} = frac{z-z_0}{n} = t $$
откуда
$$ x=x_0+lt, ;; y=y_0+mt, ;; z=z_0+nt tag{3} $$

Равенства (3) называются параметрическими уравнениями прямой L, проходящей через точку ( M_0(x_0;y_0;z_0) ) и имеющей
направляющий вектор ( vec{a}(l;m;n) ). В уравнениях (3) t рассматривается как произвольно изменяющийся параметр
( (-infty < t < +infty ) ) ; x, y, z – как функции от t. При изменении t величины x, y, z изменяются, так что точка
( M(x;y;z) ) движется по данной прямой.

Параметрические уравнения удобны в тех случаях, когда требуется найти точку пересечения прямой с плоскостью. В самом деле,
пусть непараллельные плоскость ( pi ) и прямая ( L ) заданы соответственно уравнениями
( Ax + By + Cz + D = 0 )
( x=x_0+lt, ;; y=y_0+mt, ;; z=z_0+nt )

Для определения точки пересечения прямой и плоскости подставим выражения для x, y, z из уравнений L в уравнение ( pi ).
В результате преобразований получаем
$$ t= -frac{Ax_0 + By_0 + Cz_0 + D }{Al+Bm+Cn} $$
причем знаменатель дроби не равен нулю, так как плоскость не параллельна прямой. Подставляя найденное значение t в уравнения прямой,
находим искомую точку ( M(x;y;z) ) пересечения прямой ( L ) с плоскостью ( pi ).

Угол между прямыми

Рассмотрим две прямые ( L_1 ) и ( L_2 ), заданные соответственно уравнениями

$$ frac{x-x_1}{l_1} = frac{y-y_1}{m_1} = frac{z-z_1}{n_1} $$

$$ frac{x-x_2}{l_2} = frac{y-y_2}{m_2} = frac{z-z_2}{n_2} $$

При любом расположении прямых ( L_1 ) и ( L_2 ) в пространстве один из двух углов между ними равен углу ( varphi ) между их
направляющими векторами ( vec{a_1}(l_1;m_1;n_1) ) и ( vec{a_2}(l_2;m_2;n_2) ), а второй угол равен ( 180^circ – varphi ).
Угол ( varphi ) вычисляется по следующей формуле:

$$ cos varphi = frac{l_1 l_2 + m_1 m_2 + n_1 n_2}{sqrt{l_1^2 + m_1^2 + n_1^2} ; sqrt{l_2^2 + m_2^2 + n_2^2} } $$

Источник