Как найти угол между отрезками по координатам

Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.

Для того, чтобы успешно решать задачи методом координат, полезно помнить:

Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.

Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.

Задача. Найти координаты и длины векторов  AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).

AB = (1−5; 0-8; −3−3) = (−4; −8; −6)

AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)

BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)

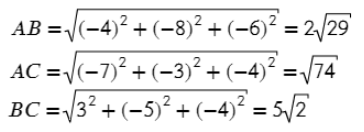
 Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):

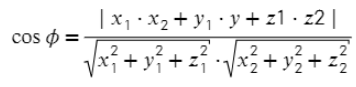
 Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

1. Находим координаты векторов.
2. Вычисляем косинус угла между векторами.
3. Через основное тригометрическое тождество получаем синус.
4. Подставляем в формулу площади.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)

AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)

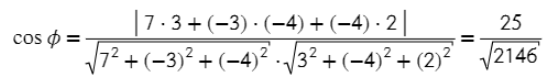
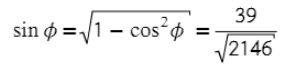
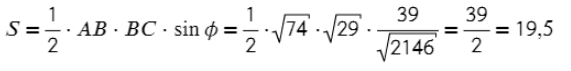
Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

1. Находим координаты векторов.
2. Задаем матрицу плоскости.
3. Вычисляем ее определитель, это и есть уравнение плоскости.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4) 

AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)

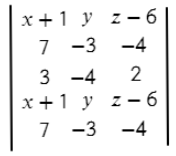Первая строчка заполняется переменными x, y, z, и из них вычитаются координаты любой точки плоскости. В данном случае вычитается точка С = (−1; 0; 6). Тогда получится такая строка: (x−(−1); y−0; z−6).

Вторая строчка – координаты первого вектора.

Третья строчка  – координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).

Четвертая заполняется аналогично первой.

Пятая – аналогично второй.

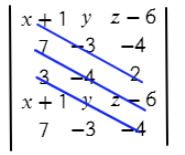
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:

(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)

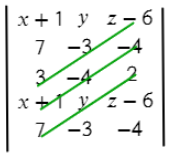
Аналогично делаем с зелеными отрезками:

(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7

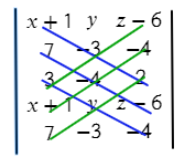
Осталось из значений синих отрезков вычесть значения зеленых отрезков:

(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =

= −22х −26y −19z + 92

−22х −26y −19z + 92  – искомое уравнение плоскости, проходящей через точки  A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета – это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.

Задача. Найдите угол между плоскостью, проходящей через точки  A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением 

14x + 6y −27z + 51 = 0.

1. Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
2. Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).

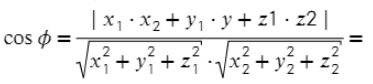
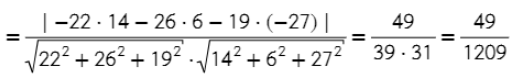
Будь в курсе новых статеек, видео и легкого математического юмора.

Угол между векторами

На изображении это α, который также можно обозначить следующим образом:

(left(widehat{overrightarrow a;overrightarrow b}right))

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как и любой другой угол, векторный может быть представлен в нескольких вариациях.

Острый:

Тупой:

Прямой:

С величиной (0^circ) (то есть, векторы сонаправлены):

С величиной (180^circ) (векторы направлены в противоположные стороны):

Нахождение угла между векторами

Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.

Формула скалярного произведения:

(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))

1. Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
2. Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
3. Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
4. Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
5. Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.

В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})

Если же координаты находятся в трехмерном пространстве и заданы в виде:

(overrightarrow a=left(a_x;a_y;a_zright))

( overrightarrow b=left(b_x;b_y;b_zright))

то формула принимает такой вид:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).

Решение

Для начала найдем их координаты по известным координатам заданных точек:

(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))

(overrightarrow{BC}=(6-2, -1-1)=(4,-2))

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})

Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)

Примеры решения задач

Для наглядности, взглянем на примеры решения задач по данной теме.

Задача 1

Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.

Решение

Применим формулу:

( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Подставим известные значения:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)

Далее найдем угол между данными векторами:

(arccosleft(-frac12right)=frac{3pi}4)

Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)

Задача 2

В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.

Решение

Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})

Подставляем значения и получаем:

(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})

Теперь находим угол α:

(alpha=arccosleft(frac2{sqrt2}right)=45^circ)

Ответ: (45^circ).

Задача 3

Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.

Решение

Для расчета используем формулу:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})

Подставим известные значения и получим:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})

Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})

Имеем три точки с координатами – A, B и C, точки образуют отрезки AB и AC, необходимо определить угол α между этими отрезками:

function getAnglePoints($x1, $y1, $x2, $y2, $x3, $y3)
{
	return rad2deg(atan2($y3 - $y1, $x3 - $x1) - atan2($y2 - $y1, $x2 - $x1));		
}

function getAnglePoints(x1, y1, x2, y2, x3, y3)
{
	return (Math.atan2(y3 - y1, x3 - x1) - Math.atan2(y2 - y1, x2 - x1)) * 180 / Math.PI;		
}