Как найти угол между пересекающимися биссектрисами - Сайт, где вы сможете решить свои вопросы

Как найти угол между биссектрисами треугольника?

Задача.

В треугольнике ABC угол C равен α, AD и BE — биссектрисы, пересекающиеся в точке O.

Найти угол AOB.

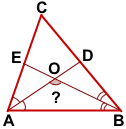Решение:

1) Так как сумма углов треугольника равна 180°, то в треугольнике ABC

∠BAC+∠ABC+∠C=180°, отсюда

∠BAC+∠ABC=180°-∠C,

∠BAC+∠ABC=180°-α.

2) Так как AD и BE — биссектрисы углов ∠BAC и ∠ABC, то

$[ angle BAO = frac{1}{2}angle BAC,angle ABO = frac{1}{2}angle ABC, ]$

$[ angle BAO + angle ABO = frac{1}{2}angle BAC + frac{1}{2}angle ABC = ]$

$[ = frac{1}{2}(angle BAC + angle ABC) = frac{1}{2}(180^o - alpha ) = 90^o - frac{alpha }{2}. ]$

3) Для треугольника AOB

∠BAO+∠ABO+∠AOB=180°,

∠AOB=180°-(∠BAO+∠ABO),

$[ angle AOB = 180^o - (90^o - frac{alpha }{2}) = 90^o + frac{alpha }{2}.]$

Замечание.

В треугольнике AOB ∠BOD — внешний угол при вершине O. Следовательно,

$[ angle BOD = angle BAO + angle ABO = 90^o - frac{alpha }{2}. ]$

Вывод:

Один уз углов, образованный при пересечении биссектрис двух углов треугольника, равен сумме 90° и половины третьего угла,

другой — разности 90° и половины третьего угла.

Запоминать для экзамена эти соотношения необязательно. Достаточно самостоятельно провести аналогичные рассуждения.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 9 апреля 2022 года; проверки требуют 32 правки.

Биссектриса AD делит пополам угол A

Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла^[1].

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.

Удобно биссектрисы треугольника обозначать следующим образом.

Если ― треугольник, и , , ― длины сторон (или просто стороны), то ${displaystyle l_{a}}$ , ${displaystyle l_{b}}$ , $l_{c}$ ― биссектрисы, проведённые соответственно из вершин , , к сторонам , , .

Связанные определения[править | править код]

Точка пересечения биссектрисы угла треугольника с его стороной, не являющейся стороной этого угла, называется основанием биссектрисы.

Свойства[править | править код]

Свойства точек пересечения биссектрис[править | править код]

Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности (инцентре).
Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами[править | править код]

Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства, связанные с дугами[править | править код]

Свойство биссектрисы вписанного угла: биссектриса вписанного угла делит на две равные части дугу, на которую этот угол опирается.
То же свойство верно и для биссектрисы центрального угла.

Свойства биссектрис равнобедренного треугольника[править | править код]

Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной внутреннему углу стороне — основанию, если треугольник равнобедренный.
У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис[править | править код]

Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть ${frac {BD}{CD}}={frac {AB}{AC}}$ или ${frac {BD}{AB}}={frac {CD}{AC}}$ .
Теорема о биссектрисе — частный случай теоремы Штейнера.
Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
Через точку Фейербаха проходит окружность, проведённая через основания трёх биссектрис.
В общем случае не пересекаются в одной точке 3 перпендикуляра к сторонам треугольника, проведённые через основания 3 внутренних его биссектрис, которые лежат на этих сторонах. ^[4]

Свойства осей биссектрис[править | править код]

Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.

Свойство проекции одной вершины на биссектрисы двух других вершин[править | править код]

Если из двух вершин треугольника провести сразу две пары биссектрис (две внутренние и две внешние), а затем на четыре полученные биссектрисы ортогонально спроектировать третью вершину, тогда полученные четыре точки проекций вершины на биссектрисы будут лежать на одной прямой (коллинеарны)^[5]. Эта прямая является средней линией треугольника, параллельной той стороне, концами которой являются упомянутые выше две вершины.

Замечание[править | править код]

В утверждении: ” Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис”,- не понятно, о каких конкретно четырёх осях биссектрис идет речь. Видимо, речь идет о каких-то осях биссектрис четырёх треугольников, фигурирующих в теореме Микеля. Возможно, что речь идет об осях внешних биссектрис или антиортовых осях этих треугольниов.

Другие свойства[править | править код]

Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
Расстояния от сторон угла до любой точки биссектрисы одинаковы.
Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно,^[6] причём даже при наличии трисектора.^[7]
Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника^[8].
Три продолжения трёх биссектрис исходного треугольника, через три их основания до их пересечения в трёх вершинах его треугольника трёх внешних биссектрис оказываются в последнем треугольнике в качестве трёх высот.

Тройки отрезков, параллельных трем бессектрисам треугольника[править | править код]

Тройки отрезков, параллельных трем бессектрисам и одновременно пересекающихся в одной точке[править | править код]

Каждый кливер есть отрезок, один конец которого находится в середине стороны треугольника и который параллелен биссектрисе угла, противоположного этой стороне. Три кливера, подобных описанному выше, пересекаются в центре Шпикера.
Если проведен отрезок с одним концом в точке касания вписанной окружности треугольника с его стороной в направлении параллельно биссектрисе угла, противоположного этой стороне, а затем для двух других сторон построены аналогичные отрезки, то эти три отрезка пересекаются в одной точке^[9].

Тройки отрезков, параллельных трем бессектрисам и одновременно образующих 2 треугольника[править | править код]

Во всякий треугольник ABC можно вписать 2 треугольника, 3 стороны которых параллельны 3 биссектрисам треугольника ABC. Эти треугольники имеют общую окружность типа окружности Эйлера, то есть 6 их вершин лежат на 1 окружности.^[10]

Длина биссектрис в треугольнике[править | править код]

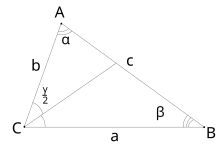
Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.

${displaystyle l_{c}={{sqrt {ab(a+b+c)(a+b-c)}} over {a+b}}={dfrac {2{sqrt {abp(p-c)}}}{a+b}}}$

, где

— полупериметр.

$l_{c}={sqrt {ab-a_{l}b_{l}}}$

$l_{c}={frac {2abcos {frac {gamma }{2}}}{a+b}}$

${displaystyle l_{c}={dfrac {2a_{l}b_{l}cos {dfrac {gamma }{2}}}{sqrt {a_{l}^{2}+b_{l}^{2}-2a_{l}b_{l}cos {(gamma })}}}}$

$l_{c}={frac {h_{c}}{cos {frac {alpha -beta }{2}}}}$

Для трёх биссектрис углов , и с длинами соответственно ${displaystyle l_{a},l_{b},}$ и $l_{c}$ , справедлива формула^[11]

${displaystyle {dfrac {(b+c)^{2}}{bc}}l_{a}^{2}+{dfrac {(c+a)^{2}}{ca}}l_{b}^{2}+{dfrac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}}$

${displaystyle w_{c}^{2}=a_{w}cdot b_{w}-ab=CE^{2}=BEcdot AE-ab}$

где:

— стороны треугольника против вершин соответственно,
— внутренние углы треугольника при вершинах соответственно,
$h_{c}$ — высота треугольника, опущенная на сторону .
$l_{c}$ — длина внутренней биссектрисы, проведённой к стороне ,
$a_{l},b_{l}$ — длины отрезков, на которые внутренняя биссектриса $l_{c}$ делит сторону ,
${displaystyle w_{c}}$ — длина внешней биссектрисы, проведённой из вершины к продолжению стороны .
${displaystyle a_{w},b_{w}}$ — длины отрезков, на которые внешняя биссектриса ${displaystyle w_{c}}$ делит сторону и её продолжение до основания самой биссектрисы.
Если медиана , высота и внутренняя биссектриса выходят из одной и той же вершины треугольника, около которого описана окружность радиуса , тогда^[12]^:p.122,#96

${displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}$

Длина частей биссектрис в треугольнике[править | править код]

Уравнения биссектрис[править | править код]

${displaystyle y={frac {a_{1}{sqrt {a_{2}^{2}+1}}pm a_{2}{sqrt {a_{1}^{2}+1}}}{{sqrt {a_{2}^{2}+1}}pm {sqrt {a_{1}^{2}+1}}}},x+{frac {b_{1}{sqrt {a_{2}^{2}+1}}pm b_{2}{sqrt {a_{1}^{2}+1}}}{{sqrt {a_{2}^{2}+1}}pm {sqrt {a_{1}^{2}+1}}}}}$

См. также[править | править код]

Антибиссектриса
Высота (геометрия)
Высота треугольника
Инцентр
Медиана треугольника
Симедиана
Теорема о биссектрисе
Ось внешних биссектрис или антиортовая ось
Треугольник
Треугольник трёх внешних биссектрис
Центроид
Чевиана

Примечания[править | править код]

↑ Иванов А. Б. Биссектриса угла // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1977. — Т. 1: А — Г. — С. 496. — 1152 стб. : ил. — 150 000 экз.
↑ Kimberling, Clark (1994), Central Points and Central Lines in the Plane of a Triangle, Mathematics Magazine Т. 67 (3): 163–187, DOI 10.2307/2690608.
↑ v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig.
↑ , . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 105.
↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 6. Глава I, п.8
↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам? Архивная копия от 18 октября 2009 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор Архивная копия от 26 августа 2015 на Wayback Machine. Дистанционный консультационный пункт по математике МЦНМО.
↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
↑ Решения заданий первого этапа Всесибирской открытой олимпиады школьников 2015-2016 г. по математике. Задача 10.3, С. 5-6// https://sesc.nsu.ru/upload/iblock/1ad/2015_1_math_s.pdf Архивная копия от 20 сентября 2022 на Wayback Machine
↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 26. Глава I. Упражнения. п.33
↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
↑ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
↑ Уравнение биссектрисы угла между двумя прямыми. Задачи повышенной трудности. Прикладная математика. Дата обращения: 3 декабря 2021. Архивировано 3 декабря 2021 года.

Литература[править | править код]

Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.

Источник

Naumenko

Высший разум

(856086)

9 лет назад

1. держа в уме задачу биссектрисы – разделить угол пополам.
2. смотря какой 4-к:
а) прямоугольник или ромб- биссектрисы взаимно перпендикулярны

б) трапеция – аналогично, тк сумма углов прилежащих к боковой стороне!!! внимание! ! 180.но есть нюансы.

в) произвольный 4-к. . особый случай.

Аркадий Жижин

Гуру

(4091)

9 лет назад

Имея углы четырёхугольника Находишь углы под биссектрисами. Далее по свойству треугольника отнимаешь сумму этих углов от 180 и всё. Если известна только сумма углов, то сумма углов под биссектрисами равна половине этой суммы и дальше так же.

Источник

Элементы треугольника. Высоты, медианы, биссектрисы

Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.

Высотой треугольника называется перпендикуляр,
опущенный из вершины треугольника
на противоположную сторону.

В тупоугольном треугольнике высота
опускается на продолжение стороны.

Три высоты треугольника всегда
пересекаются в одной точке.

В случае тупого угла пересекаются
продолжения высот.

Медианой треугольника называют отрезок,
соединяющий вершину треугольника с
серединой противоположной стороны.

Три медианы треугольника пересекаются в
одной точке и делятся в ней в отношении
2 : 1 , считая от вершины.

Биссектриса треугольника делит
угол треугольника пополам.

Три биссектрисы пересекаются в одной точке,
которая является центром окружности,
вписанной в треугольник.

Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.

Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки A на отрезок BC, зато можем опустить его на прямую BC — то есть на продолжение стороны BC.

В этом случае в одной точке пересекаются не сами высоты, а их продолжения.

В прямоугольном треугольнике каждый катет является высотой к другому катету. Три высоты прямоугольного треугольника пересекаются в вершине прямого угла.

Как доказать, что три высоты треугольника пересекаются в одной точке?
Доказательство здесь: Свойство высот треугольника.

Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.

Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2 : 1, считая от вершины.

Доказательство этой теоремы смотрите здесь: Свойства медиан треугольника.

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.

Читайте доказательство теоремы о том, что три биссектрисы треугольника пересекаются в одной точке:
Свойства биссектрис треугольника.

Еще одно свойство биссектрисы часто применяется при решении задач.

Теорема. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон:

$displaystyle frac{a}{b}=frac{m}{n}$

Доказательство этой теоремы здесь: Свойство биссектрисы треугольника.

Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.

Задача 1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.
Ответ дайте в градусах.

Решение:

Пусть биссектрисы треугольник ABC (в котором угол C равен $90^{circ}$ ) пересекаются в точке M.

Рассмотрим треугольник ABM.

, тогда $angle AM mkern -3mu B=180^{circ} - angle M mkern -3mu AB - angle AB mkern -3mu M = 180^{circ} - 0,5 left( angle ABC + angle B mkern -3mu AC right)$ .

Острый угол между биссектрисами на рисунке обозначен varphi .

Угол varphi смежный с углом AMB , следовательно, .

Поскольку треугольник ABC — прямоугольный, то $angle ABC + angle B mkern -3mu AC = 90^{circ}$ .

Тогда $varphi = 0,5 left( angle ABC + angle B mkern -3mu AC right) = 90^{circ}:2=45^{circ}$ .

Ответ: 45.

Задача 2. Острые углы прямоугольного треугольника равны $29^{circ}$ и $61^{circ}$ . Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Решение:

Пусть CH — высота, проведенная из вершины прямого угла C, CK — биссектриса угла C.

Тогда $angle AC mkern -3mu H = angle ABC = 61^{circ}$ ;

$angle AC mkern -3mu K = 90^{circ}:2=45^{circ}$ .

Угол между высотой и биссектрисой — это угол .

$angle K mkern -2mu C mkern -2mu H = angle A mkern -1mu C mkern -2mu H - angle AC mkern -3mu K = 61^{circ}-45^{circ}=16^{circ}$ .

Ответ: 16.

Задача 3. Острые углы прямоугольного треугольника равны $24^{circ}$ и $66^{circ}$ . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Решение:

Рассмотрим треугольник АВС, в котором угол С – прямой, CD – высота, СМ – медиана.

$angle CAB=24^{circ }, angle ABC=66^{circ }.$ Требуется найти угол МСD.

Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.

Следовательно, $angle MCB=angle MBC=66^{circ }.$

$angle BCD=angle BAC=24^{circ }.$

Искомый $angle MCD=angle MCB- angle BCD=66^{circ }-24^{circ }=42^{circ }.$

Ответ: 42.

Задача 4. Острые углы прямоугольного треугольника равны $27^{circ}$ и $63^{circ}$ . Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Решение:

Рассмотрим треугольник АВС, в котором угол С – прямой, CL – биссектриса, СМ – медиана.

$angle CAB=23^{circ }, angle ABC=67^{circ }.$ . Требуется найти угол МСL.

Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.

Следовательно, $angle MCB=angle MBC=67^{circ }.$

$angle BCL=angle ACL=90^{circ }:2=45^{circ },$ т.к. CL – биссектриса.

Искомый $angle MCL=angle MCB- angle BCL=67^{circ }-45^{circ }=22^{circ }.$

Ответ: 22.

Задача 5. Два угла треугольника равны $58^{circ}$ и $72^{circ}$ . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

Решение:

Из треугольника ACH (угол H — прямой) найдем угол CAH. Он равен $18^{circ}$ .

Из треугольника ACK ( K — прямой) найдем угол ACK. Он равен $32^{circ}$ .

В треугольнике AOC известны два угла. Найдем третий, то есть угол AOC, который и является тупым углом между высотами треугольника ABC:

$angle AOC = 180^{circ} - 18^{circ} - 32^{circ} = 130^{circ}$ .

Ответ: 130.

Задача 6. В треугольнике ABC угол С равен $58^{circ}$ , AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.

Решение:

Пусть в треугольнике ABC угол BAC равен A, угол ABC равен B.

Рассмотрим треугольник AOB.

, тогда $angle AO mkern -2mu B = 180^{circ} - left( angle A + angle B right)$ .

Из треугольника ABC получим, что $angle A + angle B = 180^{circ} - 58^{circ} = 122^{circ}$ .

Тогда $angle AO mkern -2mu B = 180^{circ} - left( angle A + angle B right) = 180^{circ}-61^{circ}= 119^{circ}$ .

Ответ: 119.

Задача 7. В треугольнике ABC угол A равен $60^{circ}$ , угол B равен $82^{circ}$ . AD, BD и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

Решение:

Найдем угол ACB. Он равен $38^{circ}.$

Тогда $angle AC mkern -3mu F = angle AC mkern -3mu B = 19^{circ}.$

Из треугольника ACF найдем угол $angle AF mkern -2mu C = angle AC mkern -3mu B = 19^{circ}$ . Он равен $101^{circ}$ .

Рассмотрим треугольник AOF.

$angle AF mkern -2mu O = 101^{circ}$ , $angle F mkern -3mu AO = angle B mkern -3mu AC = 30^{circ}$ . Значит $angle AO mkern -3mu F = 49^{circ}$ .

Ответ: 49.

Задача 8. В треугольнике ABC, CD — медиана, угол ACB равен $90^{circ}$ , угол B равен $58^{circ}$ . Найдите угол ACD. Ответ дайте в градусах.

Решение:

В прямоугольном треугольнике медиана равна половине гипотенузы.

Поэтому

Треугольник ADC равнобедренный, следовательно, углы при основании равны:

Поскольку в прямоугольном треугольнике сумма острых углов равна 90 градусов, получим:

$angle CAD=90^{circ }-angle ABC=90^{circ }-58^{circ }=32^{circ }.$

$angle ACD=angle CAD=32^{circ }.$

Ответ: 32.

Задача 9. В треугольнике АВС АD — биссектриса, угол С равен $50^{circ}$ . Угол САD равен $28^{circ}$ . Найдите угол В. Ответ дайте в градусах.

Решение:

Поскольку AD – биссектриса, то $angle A=2cdot angle CAD=2cdot 28^{circ }=56^{circ }.$

Сумма углов треугольника равна $180^{circ}$ , следовательно,

$angle B=180^{circ }- angle A-angle C=180^{circ }-50^{circ }-56^{circ }=74^{circ }.$

Ответ: 74.

Задача 10. В треугольнике АВС CH – высота, AD – биссектриса, О – точка пересечения прямых CH и AD, угол BAD равен $26^{circ}$ . Найдите угол АОС. Ответ дайте в градусах.

Решение:

Угол АОС – внешний в треугольнике АНО, следовательно,

$angle AOC=angle OAH+angle AHO=26^{circ }+90^{circ }=116^{circ }.$

Ответ: 116.

Задача 11. В треугольнике АВС проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника АВС. Ответ дайте в градусах.

Решение:

AD = CD, следовательно, треугольник ADC – равнобедренный и

AD – биссектриса, следовательно,

AB = AD, следовательно, треугольник ABD – равнобедренный и

– внешний в треугольнике ADC, следовательно,

Таким образом, наименьшим углом треугольника АВС является , два других угла – в два раза больше.

Воспользуемся тем, что сумма углов треугольника АВС равна $180^{circ}$ :

$angle A+angle B+angle C=2alpha +2alpha +alpha =5alpha =180^{circ }$ , откуда получаем: $alpha =180^{circ }:5=36^{circ }.$

Наименьший угол треугольника АВС равен $36^{circ}$ .

Ответ: 36.

Задача 12. Биссектриса треугольника делит противоположную сторону на отрезки 2,8 и 4,2. Периметр треугольника равен 22. Найдите стороны треугольника.

Решение:

Пусть стороны треугольника равны a, b и . Биссектриса делит сторону c на отрезки 2,8 и 4,2.
Значит,

В соответствии со свойством биссектрисы:

$displaystyle frac{a}{b}=frac{2,8}{4,2}=frac{28}{42}=frac{2}{3}.$

Или: $displaystyle a=frac{2}{3}b.$

Одновременно выполнено условие для периметра:

Тогда $displaystyle frac{5}{3}b=15, b=9, a=6.$

Ответ: 9, 6, 7.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Элементы треугольника. Высоты, медианы, биссектрисы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Биссектриса угла

Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.

Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…

Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!

Приступим!

Биссектриса угла — коротко о главном

Биссектриса угла — это линия, делящая угол пополам.

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

peresechenie bissektris v tsentre okruzhnosti

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.

bissektrisa v ravnobedrennom treugolnike

Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

bissektrisa parallelogramma otsekaet treugolnik

Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

bissektrisy vnutrennego i vneshnego uglov perpendikulyarny

Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

bissektrisy vnutrennih uglov parallelogramma

Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

( displaystyle frac{x}{y}=frac{a}{b})

bissektrisa storona treugolnika otnoshenie

А теперь подробнее…

Определение биссектрисы угла

Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?

Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):

Биссектриса угла – это линия, делящая угол пополам.

Или еще вот такое определение биссектрисы:

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

А вот определение биссектрисы треугольника:

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.

Биссектриса равнобедренного треугольника

Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.

Но представляешь, это ещё не всё. Верна ещё и обратная теорема:

Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.

Мы скоро докажем обе этих теоремы, а пока твердо запомни:

Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!

Зачем же это твердо запоминать? Как это может помочь?

А вот представь, что у тебя задача:

Дано: ( AB=5,~angle ~ABD=~angle DBC,~AD=DC. )

Найти: ( displaystyle BC. )

Ты тут же соображаешь, (displaystyle BD ) биссектриса и, о чудо, она разделила сторону ( displaystyle AC ) пополам! (по условию…).

Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.

Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!

Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике

Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?

Как это доказать?

Смотри: у ( triangle ABL ) и ( triangle CBL ) равны стороны ( AB ) и ( BC ), сторона ( BL ) у них вообще общая и ( angle 1=angle 2). (( BL ) – биссектриса!)

И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.

Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что ( triangle ABL=triangle CBL ), а значит ( AL )= ( CL ) и ( angle 3=angle 4 ).

( AL ) = ( CL ) – это уже хорошо – значит, ( BL ) оказалась медианой.

А вот что такое ( angle 3=angle 4 )?

Готов дальше?

Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.

Биссектриса, медиана, высота — определения и отличия

Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?

Если нет, не страшно. Сейчас разберемся.

Основание равнобедренного треугольника – это та сторона, которая не равна никакой другой. Посмотри на рисунок, как ты думаешь, какая это сторона? Правильно – это сторона ( AC. );
Медиана – это линия, проведенная из вершины треугольника и делящая противоположную сторону (это снова ( AC ) пополам. Заметь, мы не говорим: «Медиана равнобедренного треугольника». А знаешь почему? Потому что медиана, проведенная из вершины треугольника, делит противоположную сторону пополам в ЛЮБОМ треугольнике.;
Высота – это линия, проведенная из вершины и перпендикулярная основанию. Ты заметил? Мы опять говорим о любом треугольнике, а не только о равнобедренном. Высота в ЛЮБОМ треугольнике всегда перпендикулярна основанию.

Чем биссектриса, медиана и высота похожи между собой?

Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.

Чем биссектриса, медиана и высота отличаются между собой?

Биссектриса делит угол, из которого выходит, пополам.
Медиана делит противоположную сторону пополам.
Высота всегда перпендикулярна противоположной стороне.

Вернемся к нашим баранам — к свойствам биссектрисы…

Угол между биссектрисами любого треугольника

B ( triangle ABC )проведем две биссектрисы ( AO )и ( OC ).

Они пересеклись. Какой же угол получился у точки ( O )?

Давай его посчитаем. Ты помнишь, что сумма углов треугольника равна ( 180{}^circ ) ?

Применим этот потрясающий факт. С одной стороны, из ( triangle ABC ):

( angle A+angle B+angle C=180{}^circ ), то есть ( angle B=180{}^circ text{ }-text{ }left( angle A+angle C right) ).

Теперь посмотрим на ( triangle AOC ):

( angle 2+angle 6+angle 3=180{}^circ )

Но биссектрисы, биссектрисы же!

( angle 2=frac{angle A}{2}; angle 3=frac{angle C}{2} )

Значит ( left( triangle AOC right) )

( frac{angle A}{2}+angle 6+frac{angle C}{2}=180{}^circ ), то есть

( angle 6=180{}^circ -frac{angle A}{2}-frac{angle C}{2} );

( angle 6=180{}^circ -frac{angle A+angle C}{2} )

Вспомним про ( triangle ABC : angle A+angle C=180{}^circ -angle B )

Значит, ( angle 6=180{}^circ -frac{180{}^circ -angle B}{2}=90+frac{angle B}{2} )

Теперь через буквы

( angle AOC=90{}^circ +frac{angle B}{2} )

Не удивительно ли?

Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!

Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?

Или будет так:

Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла

Ленивые математики как обычно в двух строчках спрятали четыре.

Итак, что же значит, «Биссектриса – геометрическое место точек»? А это значит, что выполняются сразу два утверждения:

Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
Если у какой-нибудь точки расстояния до сторон угла равны, то эта точка обязательно лежит на биссектрисе.

Видишь разницу между утверждениями 1 и 2? Если не очень, то вспомни Шляпника из «Алисы в стране чудес»: «Так ты еще чего доброго скажешь, будто «Я вижу то, что ем» и «Я ем то, что вижу», — одно и то же!»

Итак, нам нужно доказать утверждения 1 и 2, и тогда утверждение: «биссектриса – это геометрическое место точек, равноудаленных от сторон угла» будет доказано!

Почему же верно 1?

Возьмём любую точку на биссектрисе и назовём её ( displaystyle A. )

Опустим из этой точки перпендикуляры ( displaystyle ) AB и ( displaystyle AC ) на стороны угла.

А теперь… Приготовились вспоминать признаки равенства прямоугольных треугольников! Если ты их подзабыл, то загляни в раздел «Прямоугольный треугольник».

Итак… Два прямоугольных треугольника: ( displaystyle AOC ) и ( displaystyle AOB. ) У них:

Почему же верно 2?

Возьмем какую-то точку ( displaystyle E) внутри угла, для которой расстояние до сторон угла равны.

И соединим точки ( displaystyle E) и ( displaystyle O).

Теперь ( displaystyle triangle EOC=triangle EOB) как прямоугольные по катету и гипотенузе.

Значит, ( displaystyle angle 1=angle 2), то есть ( displaystyle E) лежит на биссектрисе!

Вот и всё!

Как же все это применить при решении задач? Вот например, в задачах часто бывает такая фраза: «Окружность касается сторон угла….». Ну, и найти нужно что-то.

То быстро соображаешь, что:

Окружность касается сторон угла – значит, ( displaystyle AC=AB). (Правда, для этого нужно ещё знать, что радиус, проведённый в точку касания, перпендикулярен касательной)
А раз ( displaystyle AC=AB), то ( displaystyle AO) – точно биссектриса!

И можно пользоваться равенством ( displaystyle angle 1=angle 2).

Три биссектрисы в треугольнике пересекаются в одной точке

Из свойства биссектрисы быть геометрическим местом точек, равноудаленных от сторон угла, вытекает следующее утверждение:

Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

Как именно вытекает? А вот смотри: две-то биссектрисы точно пересекутся, правда?

А третья биссектриса могла бы пройти так:

Но на самом деле-то всё гораздо лучше!

Давай рассмотрим точку пересечения двух биссектрис. Назовём её ( displaystyle O).

Эта точка лежит на биссектрисе ( displaystyle AD). Что из этого следует?

Правильно! ( displaystyle OK=OM)!

Точка ( displaystyle O) лежит ещё и на биссектрисе ( displaystyle CE), поэтому ( displaystyle OK=ON).

Что мы тут оба раза применяли?

Да пункт 1, конечно же! Если точка лежит на биссектрисе, то она одинаково удалена от сторон угла.

Вот и получилось ( displaystyle OK=OM) и ( displaystyle OK=ON).

Но посмотри внимательно на эти два равенства! Ведь из них следует, что:

Переходим к следующему свойству… Ух и много же свойств у биссектрисы, правда? И это здорово, потому что, чем больше свойств, тем больше инструментов для решения задач про биссектрису.

Биссектриса и параллельность, биссектрисы смежных углов

Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например, некоторые из них:

Случай 1

Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Здорово, правда? Давай поймём, почему так.

С одной стороны, ( displaystyle angle 1=angle 2) — мы же проводим биссектрису!

Но, с другой стороны, ( displaystyle angle 2=angle 3) — как накрест лежащие углы (вспоминаем тему «Параллельные прямые»).

И теперь выходит, что:

Случай 2

Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Представь треугольник (или посмотри на картинку)

Давай продолжим сторону ( displaystyle AC) за точку ( A). Теперь получилось два угла ( displaystyle A):

( displaystyle angle 1) – внутренний угол ( displaystyle triangle ABC)
( displaystyle angle 2) – внешний угол ( displaystyle triangle ABC) – он же снаружи, верно?

Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для ( displaystyle angle 1), и для ( displaystyle angle 2). Что же получится?

bissektrisy vnutrennego i vneshnego uglov perpendikulyarny dokazatelstvo

А получится прямоугольный ( displaystyle triangle ALK)!

Удивительно, но это именно так.

Разбираемся.

bissektrisy vnutrennego i vneshnego uglov

Как ты думаешь, чему равна сумма ( displaystyle angle 1+angle 2+angle 3+angle 4)?

Случай 3

Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Видишь, что здесь все так же, как и для внутреннего и внешнего углов?

Или ещё раз подумаем, почему так получается?

Снова, как и для смежных углов,

( angle 1+angle 2+angle 3+angle 4=180{}^circ ) (как соответственные при параллельных основаниях).

И опять, ( angle 2+angle 3 ) составляют ровно половину от суммы ( angle 1+angle 2+angle 3+angle 4=180{}^circ )

Значит, ( angle 2+angle 3=90{}^circ ).

Вывод:

Биссектриса и противоположная сторона

Оказывается, биссектриса угла треугольника делит противоположную сторону не как-нибудь, а специальным и очень интересным образом:

( displaystyle frac{x}{y}=frac{a}{b})

То есть:

Отношение отрезков, на которые биссектриса поделила сторону ( displaystyle AB), такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

Удивительный факт, не правда ли?

Сейчас мы этот факт докажем, но приготовься: будет немного сложнее, чем раньше.

Снова – выход в «космос» — дополнительное построение!

Проведём прямую ( BKparallel AC).

Зачем? Сейчас увидим.

Продолжим биссектрису ( displaystyle CD) до пересечения с прямой ( displaystyle BK).

Знакомая картинка? Да-да-да, точно так же, как в пункте 4, случай 1 – получается, что ( angle 1=angle 2) (( displaystyle CD) – биссектриса)

( angle 2=angle 3) — как накрест лежащие

( Rightarrow angle 1=angle 3) и ( BC=BL)

Значит, ( BL) – это тоже ( a).

А теперь посмотрим на треугольники ( ACD) и ( BLD).

Что про них можно сказать?

Теперь можешь смело использовать! Разберём ещё одно свойство биссектрис углов треугольника. Самое сложное кончилось – будет проще.

Угол между биссектрисами треугольника

Пусть ( AO) и ( CO) – биссектрисы.

Найдём ( angle AOC) (помним, что сумма углов треугольника равна ( displaystyle 180{}^circ )).

( angle text{ }!!~!!text{ AOC}=180{}^circ -text{ }!!~!!text{ }frac{angle A}{2}-frac{angle text{C}}{2}=180{}^circ -frac{angle text{A}+angle text{C}}{2}=180{}^circ -frac{180{}^circ -angle text{B}}{2})

Получаем, что

( angle text{ }!!~!!text{ AOC}=90{}^circ +frac{angle B}{2})

Это знание можно применить в тех задачах, где участвуют две биссектрисы и дан лишь угол ( B), а искомые величины выдерживаются через ( angle AOC) или, наоборот, ( angle AOC) дан, а нужно найти что-то с участием угла ( B).

Основные знания о биссектрисе закончились. Комбинируя эти факты, ты найдёшь ключ к любой задаче о биссектрисе!

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

Связанные определения[править | править код]

Свойства[править | править код]

Свойства точек пересечения биссектрис[править | править код]

Свойства, связанные с углами[править | править код]

Свойства, связанные с дугами[править | править код]

Свойства биссектрис равнобедренного треугольника[править | править код]

Свойства оснований биссектрис[править | править код]

Свойства осей биссектрис[править | править код]

Свойство проекции одной вершины на биссектрисы двух других вершин[править | править код]

Замечание[править | править код]

Другие свойства[править | править код]

Тройки отрезков, параллельных трем бессектрисам треугольника[править | править код]

Тройки отрезков, параллельных трем бессектрисам и одновременно пересекающихся в одной точке[править | править код]

Тройки отрезков, параллельных трем бессектрисам и одновременно образующих 2 треугольника[править | править код]

Длина биссектрис в треугольнике[править | править код]

Длина частей биссектрис в треугольнике[править | править код]

Уравнения биссектрис[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Элементы треугольника. Высоты, медианы, биссектрисы

Биссектриса угла

Биссектриса угла — коротко о главном

Определение биссектрисы угла

Биссектриса равнобедренного треугольника

Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике

Биссектриса, медиана, высота — определения и отличия

Угол между биссектрисами любого треугольника

Биссектриса угла – геометрическое место точек, равноудалённых от сторон угла

Три биссектрисы в треугольнике пересекаются в одной точке

Биссектриса и параллельность, биссектрисы смежных углов

Биссектриса и противоположная сторона

Угол между биссектрисами треугольника

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Вам также может понравиться

Как найти содержанку по телефону

Как найти порно женщина с собакой

Как найти приложенное к участку цепи напряжение

Добавить комментарий Отменить ответ