Тип урока: урок изучения нового материала и первичного закрепления знаний.
Оборудование: компьютер, мультимедийный проектор, карточки, чертежи.
Задачи урока:
- Обучающая – повторить определение угла между прямой и плоскостью, признак перпендикулярности прямой и плоскости, теорему о трёх перпендикулярах , ввести определение угла между плоскостями, доказать, что угол между плоскостями не зависит от выбора точки на прямой пересечения плоскостей.
- Воспитательная – следить за чёткостью, аккуратностью, правильным выполнением чертежей, видеть связь между различными прямыми, плоскостями, воспитывать внимание, трудолюбие.
- Развивающая – развивать логическое мышление, уметь выделять главное, делать выводы, обобщать, развивать монологическую речь.
План урока
- Организационный момент.
- Проверка домашнего задания и устные упражнения ( подготовка учащихся к восприятию нового материала.
- Изучение нового материала.
- Решение задач – первичное закрепление материала.
- Решение задач с оформлением решения учителем у доски
- Запись домашнего задания.
- Проведение самостоятельной работы с проверкой в классе.
- Подведение итогов, выставление оценок.
Содержание урока
- Организационный момент.
- а) Устные упражнения.
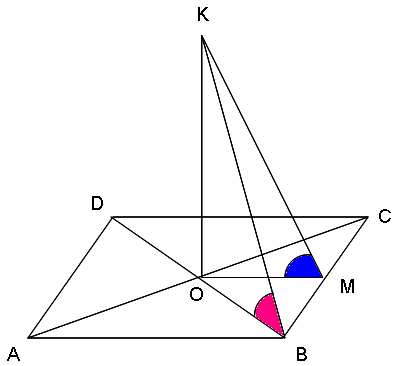
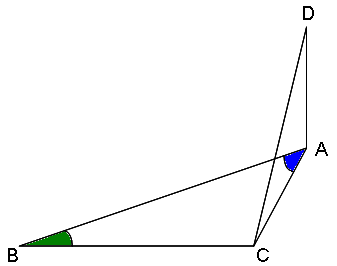
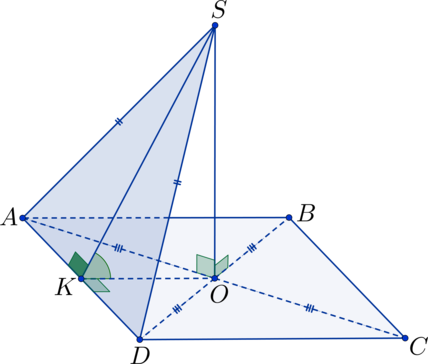
– К плоскости прямоугольника через точку пересечения его диагоналей проведён перпендикуляр ОК. Ответить на следующие вопросы:
- Назвать угол между прямой KB и плоскостью прямоугольника;
- Назвать угол между прямой КМ и плоскостью прямоугольника, где- середина стороны ВС;
- Чему равен угол между прямыми КМ и CB?
- Чему равен угол между плоскостью КОМ и прямой CB?
Презентация.
(При ответе на первые два вопроса повторяется определение между прямой и плоскостью, при ответе на третий вопрос учащимся необходимо применить теорему о трёх перпендикулярах, при ответе на четвёртый вопрос повторяется признак перпендикулярности прямой и плоскости).
Рассмотрим ответы на поставленные вопросы:
(См. рисунок №2.)
Решение задачи подготовлено в виде слайда.
1. Угол между прямой KB и плоскостью (АВС)- это угол КВО, т.к. ( по определению)угол между прямой и плоскостью- это угол между этой прямой и её проекцией на плоскость. KO – перпендикуляр, OB – проекция наклонной КВ на плоскость АВС. (При ответе на вопрос следует требовать от учащихся чёткого применения алгоритма нахождения угла между прямой и плоскостью.)
2. 1) М- это точка пересечения прямой КМ с плоскостью (АВС), т.е.
(АВС) ∩ КМ = М.
2) КО ┴ (АВС); (АВС) ∩ КО = О,
3) Соединяем точку О с точкой М, имеем ОМ- проекция КМ на плоскость (АВС), значит угол между прямой КМ и плоскостью (АВС) есть угол КМО.
3. KO – перпендикуляр, KM- наклонная, OM – проекция. Прямая CB проходит через основание наклонной и лежит в плоскости АВС, CB ┴ ОМ, т.е. CB перпендикулярна проекции ОМ, значит по теореме о трёх перпендикулярах CB ┴ КМ, значит угол между прямой CB и КМ прямой.
4. Воспользуемся признаком перпендикулярности прямой и плоскости:
CB ∩ (КОМ) = М; прямые ОМ и КМ проходят через точку пересечения прямой СВ и (КОМ); ОМ ┴ СВ; КМ ┴ СВ, значит по теореме СВ ┴ (КОМ), следовательно угол между прямой СВ и плоскостью (КОМ) –прямой.
Рисунок №1
2. б) Проверка домашнего задания.
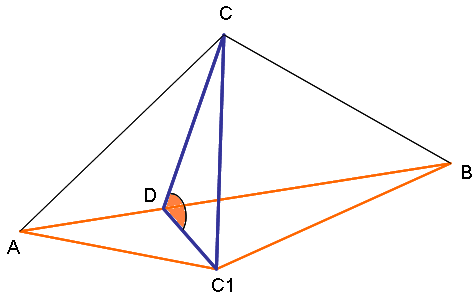
Через гипотенузу AB прямоугольного треугольника АВС проведена плоскость β. Высота СД данного треугольника образует с плоскостью β угол 60° . Найти площадь АСВ, где СС┴ β, если АС = 5, АВ =12.(См. рисунок №2.)
Решение задачи подготовлено в виде слайда.
Рисунок №2
Дано:
∆ АВС, угол АВС= 90°
CD ┴ AB
CC1 ┴ β
АС=5, AB=12
угол между прямой СD и плоскостью равен 60°
Найти: S ∆ ABC1 .
Решение:
- Отметим на чертеже угол между прямой СD и плоскостью β. СD ∩ β=D; СС1┴ β (по условию), значит DC1- проекция наклонной CD на плоскость β, значит по определению угла между прямой и плоскостью, угол CDC1- угол между прямой СD и плоскостью β; угол CDC1 =60° (по условию)
- Рассмотрим треугольник АС1В. Докажем, что С1- высота ∆ АС1В, т.е. С1D┴ АВ.
СD ┴ AB ( по условию), AB проходит через основание наклонной СD, значит по теореме обратной теореме о трёх перпендикулярах получаем, AB ┴ DС1, следовательно С1D- высота ∆ АС1В. - (При проверке домашнего задания следует особое внимание уделить стереометрической части задачи, вычислительную часть, которая теперь уже не вызывает особых затруднений, можно выписать на доске или подготовить в виде слайда без особых объяснений.)
Вид доски на втором этапе урока.
(если чертежи выполнены на доске без применения проектора)
|
Рисунок №1 Рисунок №3 |
Рисунок№2 Решение: |
Вычисления. 4. |
Переход от этапа №2 к этапу №3
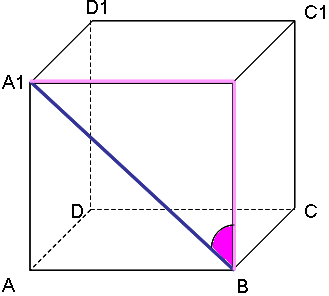
Рисунок №3.
На примере нахождения угла между прямой А1В и плоскостью ВВ1с повторяем чётко алгоритм нахождения угла между прямой и плоскостью. Воспользуемся этой идеей для определения угла между данными плоскостями.
Вид доски на втором этапе урока.
(если чертежи выполнены на доске без применения проектора)
|
Тема: Рисунок №4 |
Рисунок №1 Рисунок №3 Не стирается |
Рисунок№2 Решение: |
Вычисления. 4. Не стирается |
- Изучение нового материала.
Пусть данные плоскости пересекаются.
(См. рисунок №4)
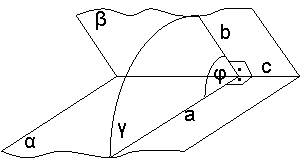
Рисунок №4.
Проведём третью плоскость, перпендикулярную линии пересечения плоскостей. Плоскость пресекает данные плоскости по двум прямым. Так вот:
«угол между этими прямыми называется углом между данными плоскостями».
– Как провести третью плоскость, перпендикулярную линии пересечения? Исходной теоремой, на которую мы будем опираться – это признак перпендикулярности прямой и плоскости.
Итак, алгоритм нахождения угла между плоскостями:
- Находим линию пересечения плоскостей.
- Через точку на линии пересечения в каждой плоскости проводим прямые, перпендикулярные линии пересечения. Они однозначно задают секущую плоскость, которая по признаку перпендикулярности прямой и плоскости будет перпендикулярна линии пересечения.
- Угол между прямыми а и в – есть угол между плоскостями.
4. Первичное закрепление материала.
(Задание предлагается в виде слайда)
Дан куб АВСDА1B1C1D1. Вычислить угол между плоскостями:
1) АDD1и АВС;
2) А1ВС и АВС.
Учащиеся проговаривают алгоритм и называют угол.
5. Решение задачи с оформлением.
Задача. Через вершину острого угла прямоугольного треугольника АВС проведён перпендикуляр АD к его плоскости. Угол АВС=30°. Вычислить угол между плоскостями BAD и CAD
Решение:
1. ∆АВС, угол C = 90°,угол АВС = 30°, значит угол САВ = 60°
2. (BAD) ∩ (CAD) = DA. По условию DA ┴ (АВС), АС ┴ DA и ВА ┴ DА (DВА) ∩ (АВС) = AB; (DАС) ∩ (АВС) = АС, значит по определению угла между плоскостями угол ВАС искомый и угол ВАС = 30°.
6. Запись домашнего задания.
7. Самостоятельная работа.
Вариант №1.
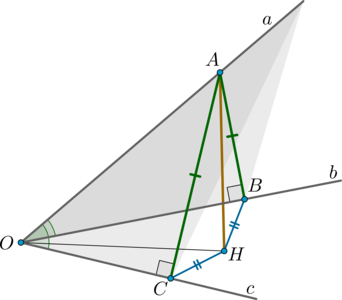
Сторона AB квадрата АВСD лежит в плоскости а. DD1перпендикулярна плоскости α. Угол между плоскостью квадрата и плоскостью α равен φ . Выполнить чертёж, отметить угол между плоскостью квадрата и плоскостью α и обосновать, что отмеченный угол, есть угол между указанными плоскостями.
Вариант №2.
Через катет МР прямоугольного треугольника МРК проведена плоскость а. Угол между плоскостью треугольника и плоскостью α равен φ. Из вершины K на плоскость α опущен перпендикуляр КВ. Выполнить чертёж, отметить угол φ и обосновать, что отмеченный угол, есть угол между указанными плоскостями.
8. Подведение итога урока.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
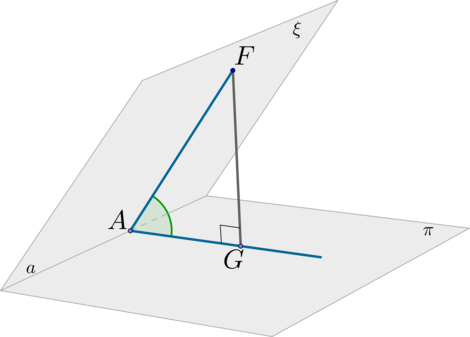
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
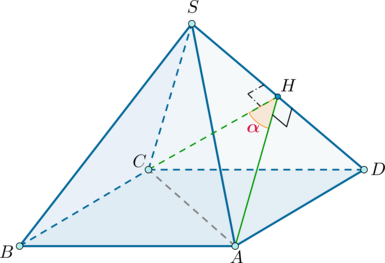
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
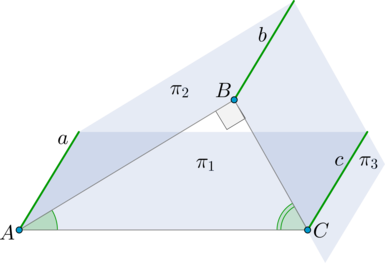
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
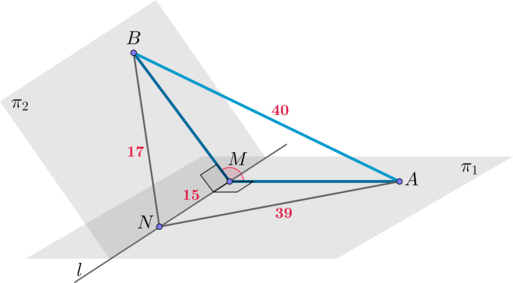
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 – 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 – 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 – 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 – 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
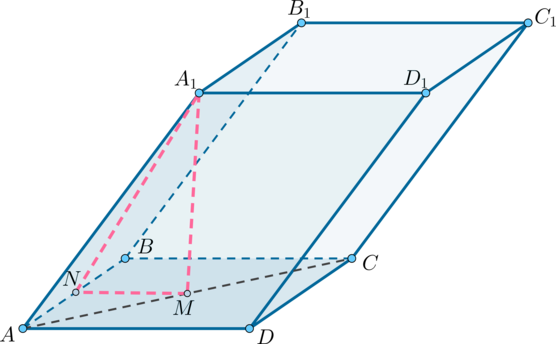
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
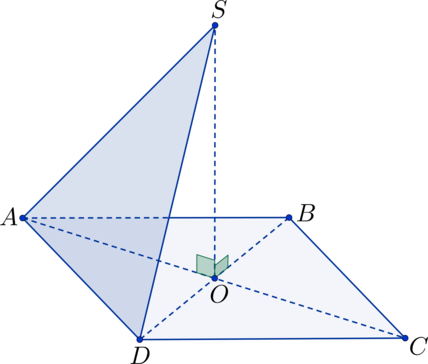
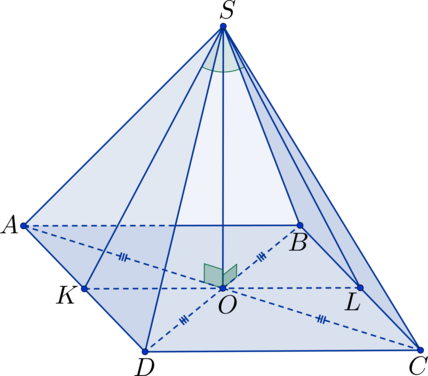
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни
Здравствуйте, дорогие подписчики и гости канала. Сегодня разбираем 13 задачу с сайта РЕШУ ЕГЭ
Вот условие задачи
Первое легко доказывается с помощью теоремы о трех перпендикулярах:
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной
Теперь зная, что А1Н перпендикурно BD легко найти угол между плоскостями – это угол между перпендикулярами, проведенными к линии пересечения плоскостей, то есть угол между А1Н и АН
Рассмотрим прямоугольный треугольник АА1Н
Найдем тангенс угла А1АН:
Спасибо за внимание
Буду рада вашим лайкам, комментариям и вашей подписке
Также приглашаю на канал в
Телеграм и в группу Вконтакте
До новых встреч на канале Простаяматематика.рф
Угол между плоскостями. Перпендикулярность плоскостей
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.
Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.
Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.
Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.
Читаем дальше: Угол и расстояние между скрещивающимися прямыми.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Угол между плоскостями. Перпендикулярность плоскостей» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
§ 14.Двугранные углы. Угол между двумя плоскостями
14.1. Двугранный угол и его измерение
Рассмотрим два полупространства, образованные непараллельными плоскостями. Пересечение этих полупространств назовём двугранным углом.
Прямую, по которой пересекаются плоскости — границы полупространств, называют ребром двугранного угла, а полуплоскости этих плоскостей, образующие двугранный угол, — гранями двугранного угла.
Двугранный угол с гранями α, β и ребром a обозначают αaβ. Можно использовать и такие обозначения двугранного угла, как K(AB)T; α(AB)β (рис. 94, 95).
Рис. 94
Рис. 95
Рис. 96
Замечание. Иногда говорят, что двугранный угол αaβ образован двумя полуплоскостями α и β, имеющими общую граничную прямую a.
Фигуры, образованные двумя страницами одной книги, двумя соседними гранями куба, — модели двугранного угла.
Для измерения двугранного угла введём понятие его линейного угла. На ребре a двугранного угла αaβ отметим произвольную точку O и в гранях α и β проведём из точки O соответственно лучи OA и OB, перпендикулярные ребру a (рис. 96, а). Угол AOB, образованный этими лучами, называется линейным углом двугранного угла αaβ.
Так как OA ⊥ a и OB ⊥ a, то плоскость AOB перпендикулярна прямой a. Это означает, что линейный угол двугранного угла есть пересечение данного двугранного угла и плоскости, перпендикулярной его ребру.
Вследствие произвольного выбора точки O на ребре двугранного угла заключаем, что двугранный угол имеет бесконечное множество линейных углов. Докажем, что все они равны. Действительно, рассмотрим два линейных угла AOB и A1O1B1 двугранного угла αaβ (рис. 96, б). Лучи OA и O1A1 лежат в одной грани α и перпендикулярны прямой a — ребру двугранного угла, поэтому они сонаправлены. Аналогично получаем, что сонаправлены лучи OB и O1B1. Тогда ∠ AOB = ∠ A1O1B1 (как углы с сонаправленными сторонами).
Таким образом, нами доказана теорема.

Иначе говоря, все линейные углы данного двугранного угла равны между собой.
Это позволяет ввести следующее определение.
Определение. Величиной двугранного угла называется величина его линейного угла.
Рис. 97
Величина двугранного угла, измеренная в градусах, принадлежит промежутку (0°; 180°).
На рисунке 97 изображён двугранный угол, градусная мера (величина) которого равна 30°. В этом случае также говорят, что двугранный угол равен тридцати градусам.
Двугранный угол является острым (рис. 98, а), прямым (рис. 98, б) или тупым (рис. 98, в), если его линейный угол соответственно острый, прямой или тупой.
Рис. 98
Заметим, что аналогично тому, как и на плоскости, в пространстве определяются смежные (рис. 99, а) и вертикальные (рис. 99, б) двугранные углы. При этом справедливы и аналогичные теоремы о величинах этих углов.
Попробуйте доказать самостоятельно следующие два утверждения, важные для решения задач.
На гранях двугранного угла величины α взяты точки A и B; A1 и B1 — проекции этих точек на ребро двугранного угла; AA1 = a; BB1 = b; A1B1 = h. Тогда
AB = 
Рис. 99
Если внутри двугранного угла величины α взята точка на расстояниях a и b от граней двугранного угла, то её расстояние от ребра двугранного угла равно 
14.2. Угол между двумя плоскостями
Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром (рис. 100). Если величина одного из них равна ϕ, то величины трёх остальных равны соответственно 180° – ϕ, ϕ, 180° – ϕ (почему?). Наименьшая из этих величин принимается за величину угла между данными пересекающимися плоскостями.
Определение. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении.
Угол между параллельными или совпадающими плоскостями полагается считать равным нулю.
Если величина угла между плоскостями α и β равна ϕ, то пишут: 
Рис. 100
Так как двугранный угол измеряется своим линейным углом, то из выше приведённого определения следует, что угол между пересекающимися плоскостями равен углу между пересекающимися прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения (см. рис. 100). Это означает, что величина угла между плоскостями принадлежит промежутку [0°; 90°].
Рис. 101
ЗАДаЧа. Отрезок DM длиной 3,2 перпендикулярен плоскости ромба ABCD (∠ ADC — тупой). Диагонали ромба равны 12 и 16. Найти углы между плоскостями:
а) ABC и MBC; б) AMD и CMD.
Решение. а) Пусть DE — высота ромба ABCD (рис. 101). Тогда по теореме о трёх перпендикулярах ME ⊥ BC и ∠ DEM = ϕ — линейный угол двугранного угла, образованного плоскостями ABC и MBC. Найдём величину этого угла.
По условию задачи DM ⊥ (ABC), поэтому ⧌ MDE — прямоугольный, значит, tg ϕ = 



Учитывая, что S = 






б) Так как отрезок DM — перпендикуляр к плоскости ромба ABCD, то AD ⊥ DM, CD ⊥ DM, значит, ∠ ADC = ψ — линейный угол двугранного угла, образованного пересекающимися плоскостями ADM и CDM. Найдём этот угол.
В треугольнике ACD по теореме косинусов находим
cos ψ = 


откуда ψ = arccos 
Ответ: а) arctg