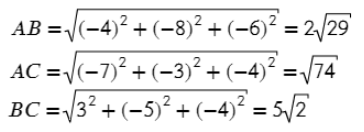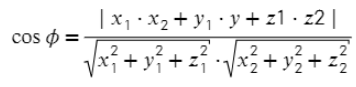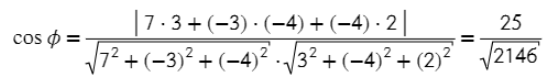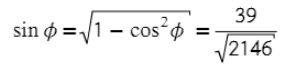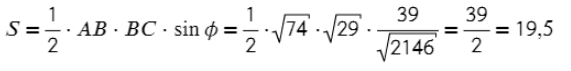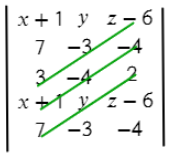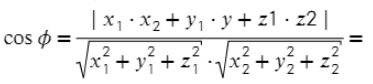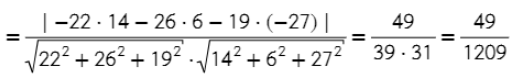Как найти угол между плоскостями через векторы

Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.

---

Для того, чтобы успешно решать задачи методом координат, полезно помнить:

Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.

Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.

Задача. Найти координаты и длины векторов  AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).

AB = (1−5; 0-8; −3−3) = (−4; −8; −6)

AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)

BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)

 Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):

 Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

1. Находим координаты векторов.
2. Вычисляем косинус угла между векторами.
3. Через основное тригометрическое тождество получаем синус.
4. Подставляем в формулу площади.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)

AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)

Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

1. Находим координаты векторов.
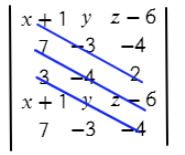
2. Задаем матрицу плоскости.
3. Вычисляем ее определитель, это и есть уравнение плоскости.

AB = (3−(−4); 1−4; 0−4) = (7; −3; −4) 

AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)

Первая строчка заполняется переменными x, y, z, и из них вычитаются координаты любой точки плоскости. В данном случае вычитается точка С = (−1; 0; 6). Тогда получится такая строка: (x−(−1); y−0; z−6).

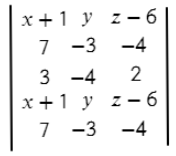
Вторая строчка – координаты первого вектора.

Третья строчка  – координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).

Четвертая заполняется аналогично первой.

Пятая – аналогично второй.

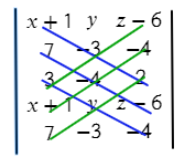
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:

(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)

Аналогично делаем с зелеными отрезками:

(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7

Осталось из значений синих отрезков вычесть значения зеленых отрезков:

(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =

= −22х −26y −19z + 92

−22х −26y −19z + 92  – искомое уравнение плоскости, проходящей через точки  A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).

P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета – это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.

Задача. Найдите угол между плоскостью, проходящей через точки  A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением 

14x + 6y −27z + 51 = 0.

1. Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
2. Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).

Будь в курсе новых статеек, видео и легкого математического юмора.

Как найти угол между двумя плоскостями?

Пусть заданы уравнениями две плоскости $$A_1 x + B_1 y + C_1 z + D_1 = 0$$ $$A_2 x + B_2 y + C_2 z + D_2 = 0$$

Запишем нормальные векторы этих плоскостей, каждая координата которых равна соответствующим коэффициентам в уравнениях плоскостей $$overline{n}_1 = (A_1,B_1,C_1)$$$$overline{n}_2 = (A_2,B_2,C_2)$$

Угол между плоскостями – это угол между двумя нормальными векторами этих плоскостей, вычисляемый по формуле: $$cos varphi = frac{(overline{n}_1,overline{n}_2)}{|overline{n}_2| cdot |overline{n}_2|}$$

В числителе формулы стоит скалярное произведение векторов, вычисляемое путем суммирования произведений соответствующих координат

$$(overline{n}_1,overline{n}_2) = A_1 cdot A_2 + B_1 cdot B_2 + C_1 cdot C_2$$

В знаменателе расположено произведение длин векторов, вычисляемых извлечением квадратного корня из суммы квадратов соответствующих координат векторов

$$|overline{n}_1| = sqrt{A_1 ^2 + B_1 ^2 + C_1 ^2}$$

$$|overline{n}_2| = sqrt{A_2 ^2 + B_2 ^2 + C_2 ^2}$$

1. Вычисляем скалярное произведение нормальных векторов $(overline{n}_1,overline{n}_2)$
2. Находим произведение модулей нормальных векторов $ |overline{n}_1| cdot |overline{n}_2| $
3. Подставляем найденные значения в формулу косинуса угла между плоскостями $ cos varphi $

Примеры решений

Пример 1

Найти угол между плоскостями $3x-y+3=0$ и $x-2y+5z-10=0$

Решение

Записываем нормальные векторы каждой из плоскостей. В качестве координат векторов подставляем коэффициенты из уравнений плоскостей $$ overline{n}_1 = (3,-1,0) $$ $$ overline{n}_2 = (1,-2,5) $$ Вычисляем скалярное произведение, полученных векторов $overline{n}_1$ и $ overline{n}_2$. Выполняем сложение произведений соответствующих координат $$(overline{n}_1,overline{n}_2) = 3cdot 1 + (-1)cdot (-2) + 0cdot 5 = 5$$ Находим модули каждого из векторов. Извлекаем квадратный корень из суммы квадратов соответствующих координат $$|overline{n}_1| = sqrt{3^2 + (-1)^2 + 0^2} = sqrt{10}$$ $$|overline{n}_2| = sqrt{1^2+(-2)^2+5^2} = sqrt{30}$$ Подставляем полученные значения в формулу нахождения угла между плоскостями $$cos varphi = frac{5}{sqrt{10} cdot sqrt{30}} = frac{1}{sqrt{12}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$varphi = arccosfrac{1}{sqrt{12}}$$

Рассмотрим
две плоскости α1 и α2, заданные соответственно
уравнениями:

Под
углом между двумя плоскостями будем
понимать один из двугранных углов,
образованных этими плоскостями. Очевидно,
что угол между нормальными

Под
углом между двумя плоскостями будем
понимать один из двугранных углов,
образованных этими плоскостями. Очевидно,
что угол между нормальными векторами
п1 и п2 плоскостей α1 и α2 равен одному из
указанных смежных двугранных углов

двугранных
углов

или

Поэтому

Т.к.

и

, то

17.Условия параллельности и перпендикулярности плоскостей.

Условие
перпендикулярности плоскостей.

Ясно,
что две плоскости перпендикулярны тогда
и только тогда, когда их нормальные
векторы перпендикулярны, а следовательно
,
или

.

Таким
образом, .

Условие
параллельности двух плоскостей.

Две
плоскости α1 и α2 параллельны тогда и
только тогда, когда их нормальные векторы
п1 и п2 параллельны, а значит .

Итак,
две плоскости параллельны друг другу
тогда и только тогда, когда коэффициенты
при соответствующих координатах
пропорциональны:

или

18.Прямая в пространстве: общие, параметрические и канонические уравнения, их эквивалентность; уравнения прямой, проходящей через две данные точки.

ОБЩИЕ
УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ
ДВУХ ПЛОСКОСТЕЙ

Через
каждую прямую в пространстве проходит
бесчисленное множество плоскостей.
Любые две из них, пересекаясь, определяют
ее в пространстве. Следовательно,
уравнения любых двух таких плоскостей,
рассматриваемые совместно представляют
собой уравнения этой прямой.

Вообще
любые две не параллельные плоскости,
заданные общими уравнениями

определяют
прямую их пересечения. Эти уравнения
называются общими уравнениями прямой.

–Пусть
заданы две точки М1(х1, у1, z1)
и М2(х2, у2, z2),
через которые должна проходить прямая
линия. Примем за направляющий вектор
прямой вектор

.

Поэтому
уравнение (13.4) примет вид

Положение
прямой в пространстве вполне определяется
заданием какой-либо её фиксированной
точки М1 и S
вектора , параллельного этой прямой.

Вектор
S,
параллельный прямой, называется
направляющим вектором этой прямой.

Итак,
пусть прямая l проходит через точку
М1(x1, y1, z1), лежащую на прямой параллельно
вектору

.

Рассмотрим
произвольную точку М(x,y,z) на прямой. Из
рисунка видно, что

Векторы

и коллинеарны, поэтому найдётся такое
число t, что

,
где множитель t может принимать любое
числовое значение в зависимости от
положения точки M на прямой. Множитель
t называется параметром. Обозначив
радиус-векторы точек М1 и М соответственно
через

и

,
получаем . Это уравнение называется
векторным уравнением прямой. Оно
показывает, что каждому значению
параметра t соответствует радиус-вектор
некоторой точки М, лежащей на прямой.

Запишем
это уравнение в координатной форме.
Заметим, что ,

и

и

отсюда

Полученные
уравнения называются параметрическими
уравнениями прямой.

При
изменении параметра t изменяются
координаты x, y и z и точка М перемещается
по прямой.

КАНОНИЧЕСКИЕ
УРАВНЕНИЯ ПРЯМОЙ

Пусть
М1(x1, y1, z1) – точка, лежащая на прямой l, и

– её направляющий вектор. Вновь возьмём
на прямой произвольную точку М(x,y,z) и
рассмотрим вектор

.

Ясно,
что векторы

и S
коллинеарные, поэтому их соответствующие
координаты должны быть пропорциональны,
следовательно,

–
канонические
уравнения прямой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Угол между плоскостями.

Определение.

Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.

Определение.

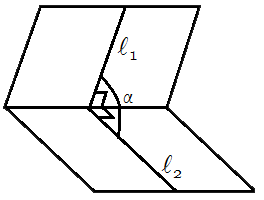
Двугранный угол между плоскостями равен углу образованному прямыми l₁ и l₂, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

Формула для вычисления угла между плоскостями

Если заданы уравнения плоскостей A₁x + B₁y + C₁z + D₁ = 0 и A₂x + B₂y + C₂z + D₂ = 0, то угол между плоскостями можно найти, используя следующую формулу

cos α =	|A1·A2 + B1·B2 + C1·C2|
√A12 + B12 + C12√A22 + B22 + C22

Примеры задач на вычисление угла между плоскостями

Пример 1.

Найти угол между плоскостями 2x + 4y – 4z – 6 = 0 и 4x + 3y + 9 = 0.

Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:

cos α =

|2·4 + 4·3 + (-4)·0|√2² + 4² + (-4)²√4² + 3² + 0²

=

|8 + 12|√36√25

=

2030

=

23

Ответ: косинус угла между плоскостями равен cos α = 23.

19
Мар 2012

13 Задание (2022) (C2)ВИДЕОУРОКИ

Угол между плоскостями. Метод координат. Задание 14

|
Отзывов (50)
| Метки: решение задания С2