Цели урока:
Образовательные:
- изучить некоторые методы нахождения расстояний и углов в пространстве, такие как метод параллельных плоскостей, метод объёмов, с использованием теоремы о площади ортогональной проекции многоугольника;
- повторить основные способы решения задач нахождения расстояний и углов в пространстве: по определению и метод координат;
- проверить знание формул нахождения расстояний и углов в пространстве;
- проверить умения решать простейшие задачи на нахождение углов между прямыми и плоскостями в пространстве.
Ход урока
1. Организационный момент.
2. Вступительное слово.
Цели нашего урока – повторить координатный метод решения задач нахождения расстояний и углов в пространстве, познакомиться с избранными методами решения задач на нахождение расстояний и углов в пространстве, научиться применять их при решении задач.
Начнем урок с устной работы, цель которой – повторить определения и формулы, которые нам понадобятся для нахождения расстояний и углов в пространстве.
3. Работа устно.
Найти соответствие между левой и правой частями формул.
4. Тренажер.
Заполнить пропуски в решении.
1. Точка К – середина ребра АA1 куба АВСDA1B1C1D1. Найдите угол между прямыми A1В и СК.
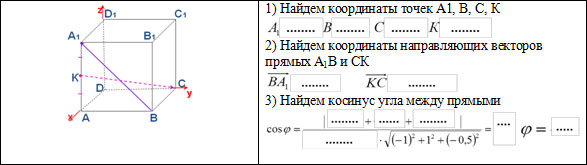
2. В правильной треугольной призме АВСA1B1C1 стороны основания равны 2, а боковые ребра равны 4. Точка D – середина ребра CC1. Найдите расстояние от вершины С до плоскости АDB1.
3. Основание прямой четырехугольной призмы прямоугольник ABCD, в котором AB = 12, AD = Найдите косинус угла между плоскостью основания и плоскостью, проходящей через середину ребра A1D1 перпендикулярно прямой BD1, если расстояние между прямыми AC и B1D1 равно 5.
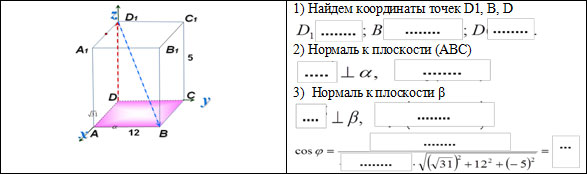
5. Избранные методы нахождения расстояний и углов в пространстве.
Каждая из трех групп за неделю до урока получила кейсы с методами решения задач. На уроке один представитель от группы показывает презентацию по решению задачи указанным способом.
1 группа (метод параллельных плоскостей).
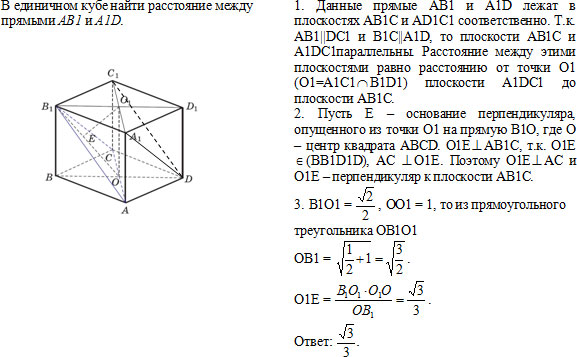
Вывод. Чтобы найти расстояние между скрещивающимися прямыми методом параллельных плоскостей, надо:
- Определить параллельные плоскости, в которых лежат прямые.
- Переформулировать данную задачу как задачу на нахождение расстояния от точки до плоскости.
- Построить расстояние от точки до плоскости.
- Найти это расстояние.
2 группа (метод объёмов).
Вывод. Чтобы найти расстояние от точки до плоскости методом объёма, надо:
- Построить искомое расстояние.
- Определить пирамиду, содержащую это расстояние.
- Найти объем этой пирамиды, используя равенство объёмов одной фигуры, выраженной двумя независимыми формулами.
- Воспользоваться формулой
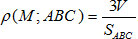
3 группа (с использованием теоремы о площади ортогональной проекции многоугольника).
Вывод. Чтобы найти угол между плоскостями методом ортогональной проекции, надо:
- Определить площадь многоугольника, лежащего в одной из плоскостей.
- Определить площадь его ортогональной проекции на другую плоскость.
- Воспользоваться формулой
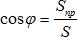
6. Составление памятки по методам решения задач на нахождение углов и расстояний в пространстве
Памятка по решению задач на нахождение углов и расстояний в пространстве
Способы решения задач на нахождение углов и расстояний в пространстве:
- Геометрический;
- Координатный;
- Метод параллельных плоскостей:
а) Определить параллельные плоскости, в которых лежат прямые.
б) Переформулировать данную задачу как задачу на нахождение расстояния от точки до плоскости.
в) Построить расстояние от точки до плоскости.
г) Найти это расстояние. - Метод объемов:
а) Построить искомое расстояние.
б) Определить пирамиду, содержащую это расстояние.
в) Найти объем этой пирамиды, используя равенство объёмов одной фигуры, выраженной двумя независимыми формулами.
г) Воспользоваться формулой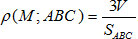 - С использованием теоремы о площади ортогональной проекции многоугольника:
а) Определить треугольник, который является ортогональной проекцией многоугольника на плоскость.
б) Найти площадь этого многоугольника.
в) Найти ортогональной проекции.
г) Воспользоваться формулой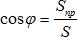
7. Работа в группах.
- Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от точки А до плоскости, проходящей через середины ребер АВ, АС и АD, если AD = =2√5, AB = AC =10, BC = 4√5 (решить методом объёмов).
- В правильной шестиугольной призме A…F1, стороны основания которой равны 1, а боковые ребра равны 2, найти угол между плоскостями BA1D1 и AA1E1 (решить методом ортогонального проектирования).
8. Подведение итогов.
- Какие методы нахождения расстояний и углов в пространстве вы узнали сегодня на уроке?
- Сможете ли вы самостоятельно находить расстояния и углы в пространстве?
- Какой из методов нахождения расстояний и углов в пространстве вы считаете наиболее приемлемым для вас?
- Чувствовали ли себя комфортно на уроке?
Построение угла между двумя плоскостями
Мерой угла между плоскостями является острый угол, образованный двумя прямыми, лежащими в этих плоскостях и проведенными перпендикулярно линии их пересечения.
Алгоритм построения
- Из произвольной точки K проводят перпендикуляры к каждой из заданных плоскостей.
- Способом вращения вокруг линии уровня определяют величину угла γ° с вершиной в точке K.
- Вычисляют угол между плоскостями ϕ° = 180 – γ° при условии, что γ° > 90°. Если γ° < 90°, то ∠ϕ° = ∠γ°.
Задача 1
На рисунке представлен случай, когда плоскости α и β заданы следами. Все необходимые построения выполнены согласно алгоритму и описаны ниже.
Решение
- В произвольном месте чертежа отмечаем точку K. Из неё опускаем перпендикуляры m и n соответственно к плоскостям α и β. Направление проекций m и n следующее: m”⊥f0α, m’⊥h0α, n”⊥f0β, n’⊥h0β.
- Определяем действительный размер ∠γ° между прямыми m и n. Для этого вокруг фронтали f поворачиваем плоскость угла с вершиной K в положение, параллельное фронтальной плоскости проекции. Радиус поворота R точки K равен величине гипотенузы прямоугольного треугольника O”K”K0, катет которого K”K0 = yK – yO.
- Искомый угол ϕ° = ∠γ°, поскольку ∠γ° острый.
Задача 2
На рисунке ниже показано решение задачи, в которой требуется найти угол γ° между плоскостями α и β, заданными параллельными и пересекающимися прямыми соответственно.
Решение
- Определяем направление проекций горизонталей h1, h2 и фронталей f1, f2, принадлежащих плоскостям α и β, в порядке, указанном стрелками. Из произвольной точки K на пл. α и β опускаем перпендикуляры e и k. При этом e”⊥f”1, e’⊥h’1 и k”⊥f”2, k’⊥h’2.
- Определяем ∠γ° между прямыми e и k. Для этого проводим горизонталь h3 и вокруг неё поворачиваем точку K в положение K1 , при котором △CKD станет параллелен горизонтальной плоскости и отразится на ней в натуральную величину – △C’K’1D’. Проекция центра поворота O’ находится на проведенном к h’3 перпендикуляре K’O’. Радиус R определяется из прямоугольного треугольника O’K’K0, у которого сторона K’K0 = ZO – ZK.
- Значение искомого ∠ϕ° = ∠γ°, так как угол γ° острый.
Угол между плоскостями.
Стереометрия
Пусть
плоскости α и β пересекаются по прямой с.
Угол между
плоскостями — это угол между перпендикулярами к линии их пересечения,
проведенными в этих плоскостях.
Другими словами, в плоскости
α мы провели прямую а, перпендикулярную с. В плоскости
β — прямую b, также перпендикулярную с. Угол между плоскостями
α и β равен углу между прямыми а и b.
Заметим, что при пересечении двух
плоскостей вообще-то образуются четыре угла. В качестве угла между
плоскостями мы берем острый угол.
Метод координат
Угол между плоскостями равен углу,
образованному нормальными векторами этих плоскостей.
Если векторы n1 и n2 – нормальные векторы данных плоскостей, то угол между плоскостями
вычисляется по формуле
cosγ = 
Если заданы уравнения
плоскостей A1x + B1y + C1z + D1 = 0
и A2x + B2y + C2z + D2 = 0,
то 
и 
– нормальные векторы этих плоскостей.
Тогда угол между плоскостями
можно найти, используя следующую формулу
cos γ=
,
Задача. В
правильной четырехугольной призме со стороной основания 12 и
высотой 21 на ребре АА1 взята
точка М так, что АМ=8. На ребре ВВ1 взята точка K так, что В1К = 8. Найдите угол между плоскостьюD1MK и
плоскостью CC1D1.
Решение.
АD1 ⊥( CC1D1), значит АD1 = n1
Найдем n2 
⊥(D1MK).
n2⊥D1M, А1М=21-8=13, М(0;0;13), D1(
, значит
D1M
n2⊥ MK,
М(0;0;13),К(12;0;8), значит MK
n2•D1M=0 -12у+13z=0 y=
n2• MK=0 12x-5z=0 x=
Примем z=12, тогда х=5,у=13 , тогда n2
.
cosγ = 
cosγ =
=
=
=
=
, откуда
γ=450.
Ответ: 450.
Использование
теоремы о площади ортогональной проекции многоугольника.
Угол между
плоскостями α и β можно вычислить, используя формулу
cosγ =
Три
способа решения одной задачи.
Задача. 
На
ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1
взята точка E так, что A1E : EA =
4 : 3. Точка T — середина ребра B1C1.
Известно, что AB = 5, AD = 8, AA1 =
14.
а) В
каком отношении плоскость ETD1 делит ребро BB1?
б)
Найдите угол между плоскостью ETD1 и
плоскостью AA1B1.
Решение.
1 способ – геометрический
а) Так
как 
и 
то 
и 
Плоскость
сечения пересекает параллельные плоскости 
и 
по
параллельным прямым, поэтому 
∥ 
Значит, треугольники 
и 
подобны(
по углам с соответственно параллельными сторонами).
= 
, откуда 
=
= 
=4
Значит, QB= BB1– QB1= 14-4=10 и QB:QB1=10:4=5:2.
б) Так как прямая 
⊥ 
опустим проведём
⊥
– линии пересечения
плоскостей. ETD1 и AA1B1.
По теореме о трех перпендикулярах так как ⊥,то
и D1H⊥
.
Угол 
будет
искомым.
Найдём 
Для
этого проведём в трапеции 
высоту
= А1В1.
По теореме Пифагора 
=
= 
.
Теперь,
вычисляя двумя способами площадь треугольника 
найдём
S =
то есть А1H= 
= 
Тогда из треугольника А1HD, где угол А1 прямой, найдем тангенс искомого угла
равен tg H = 8: 
= 
.
Ответ: а) 
б) arctg
Решение.
2 способ – метод координат
б) Введем прямоугольную
систему координат с началом в точке А. Угол между ЕТD1 и AA1B1 будем искать по
формуле
cosγ = 
АD ⊥( AA1B1), значит АD = n1
Найдем n2 ⊥( ЕТD1).
n2⊥EQ, Е(0;0;6), Q(
, значит
EQ
n2⊥ED1, Е(0;0;6), D1 (8;0;14), значит ED1
n2• EQ =0 5у+4z=0 y=
n2• ED1=0 8x+8z=0 x= – z
Примем z=5, тогда х= – 5,у=- 4 , тогда n2
.
cosγ = 
cosγ =
=
=
Ответ:б) arccos
Решение.
3 способ – метод проекций
Угол между
плоскостью ETD1 и плоскостью AA1B1
можно вычислить, используя формулу
cosγ =
– площадь
трапеции EQTD1, 
– площадь
трапеции А1В1QE.
=
=
(В1Q +
А1E)• А1В1= 
(4+8)•5= 30
=
= 
(QT+ ED1)•QР, где QР – высота.
Из треугольника A1D1E D1E=
=8
Из треугольника B1QT QT
=4
Из треугольника LQE QE=
=
Из треугольника C1D1T D1T ==
Трапеция EQTD1 – равнобедренная. РЕ = (8 – 4):2=2
Из треугольника РQE QР= 
=
== (QT+ ED1)•QР=(8
4
• :2= 6
cosγ == 
=
Ответ: б) arccos
Мерой угла между двумя плоскостями служит линейный угол, образованный двумя прямыми – сечениями граней этого угла плоскостью, перпендикулярной к их ребру.
Для построения линейного угла, являющегося мерой двугранного угла, необходимо выполнить следующие геометрические построения:
1. Определить прямую а – линию пересечения данных плоскостей α и β, а = α ∩ β (рис. 284).
2. Провести плоскость γ (γ ⊥ α и γ ⊥ β).
3. Построить прямые m = γ ∩ α и n = γ ∩ β.
4. Найти величину угла 
между прямыми m и n. Угол – искомый.
Рассмотренный план решения задачи предусматривает выполнение большого числа геометрических построений, связанных с нахождением линии пересечения данных плоскостей (а = α ∩ β), проведением плоскости, перпендикулярной к найденной прямой (γ ⊥ а ). Далее приходится еще дважды решать задачу по определению линии пересечения плоскостей (m = γ ∩ α и n = γ ⊥ β) и лишь только после этого можно приступить к определению величины искомого угла .
Проследим, как можно упростить решение этой задачи. Дополним чертеж на рис. 284 точкой К ∈ γ и опустим из этой точки перпендикуляры k и l на плоскости α и β (рис. 285). Точки М и N пересечения
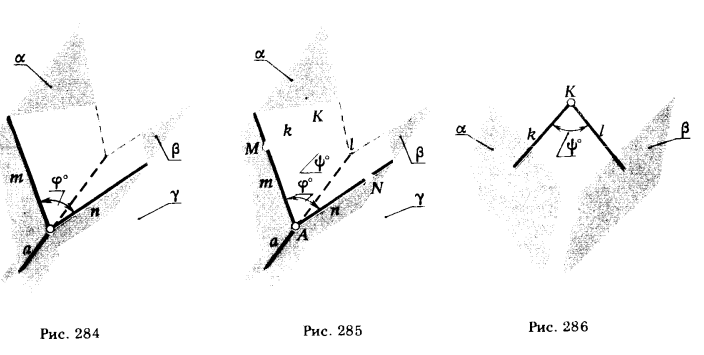
этих перпендикуляров с плоскостями совместно с точками К и А (А ∈ а ) являются вершинами плоского четырехугольника KNAM, у которого углы при вершинах М и N прямые. Следовательно, между углами при вершинах А и К существует зависимость, которую можно выразить следующим равенством: = 180° – ψ°. Из рис. 285 видно, что вместо ∠ψ° гораздо проще определять дополнительный до 180° ∠ψ°. Все решение сводится к построению угла ψ° путем проведения из произвольной точки пространства К прямых k и l, перпендикулярных к заданным плоскостям, и определению угла ψ° между этими прямыми; после чего подсчитывается значение величины = 180° –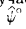 
(рис. 286).
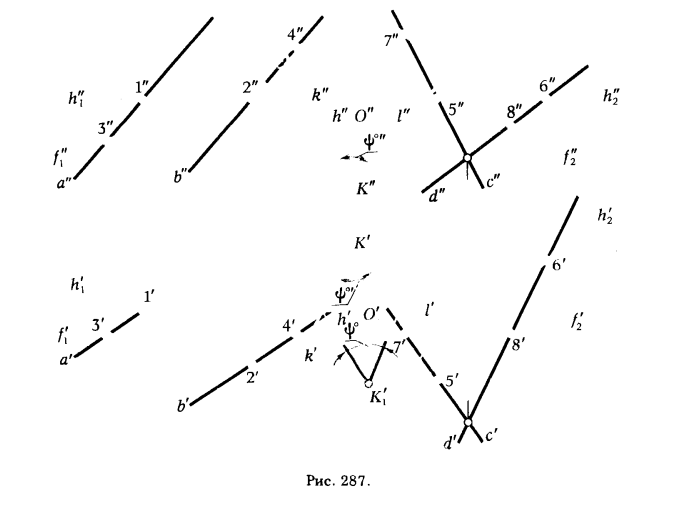
ПРИМЕР 1. Определить угол между плоскостями α(а || b) и β(с ∩ d) (рис. 287).
РЕШЕНИЕ.
1. Определяем направление горизонтальных проекций горизонталей h’1 и h’2, фронтальных проекций фронталей f”1 и f”2 заданных плоскостей α и β.
2. Из произвольной точки К проводим проекции перпендикуляров k и l (k’ ⊥ h’1, k” ⊥ f”1 и l’ ⊥ h’2, l” ⊥ f”2).
3. Определяем величину .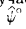
4. Вычисляем значение = 180° – .
Если плоскости, угол между которыми требуется определить, задан следами, то решение упрощается еще больше, так как отпадает необходимость в выполнении п.1 только что рассмотренного решения.
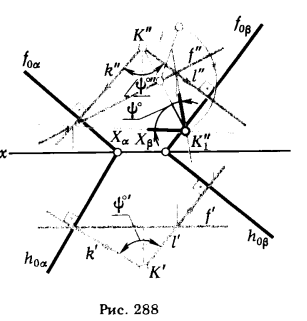
ПРИМЕР 2. Определить угол между плоскостями α и β, заданными следами (рис. 288)
РЕШЕНИЕ. Все геометрические построения сводятся к проведению через точку К прямых, перпендикулярных к следам плоскостей α и β (k’ ⊥ h0α, k” ⊥ f0α и l’ ⊥ h0β, l” ⊥ f0β). Затем известным способомнаходим величину (на рис. 288 угол определен путем вращения вокруг фронтали). Зная , вычисляем значение .
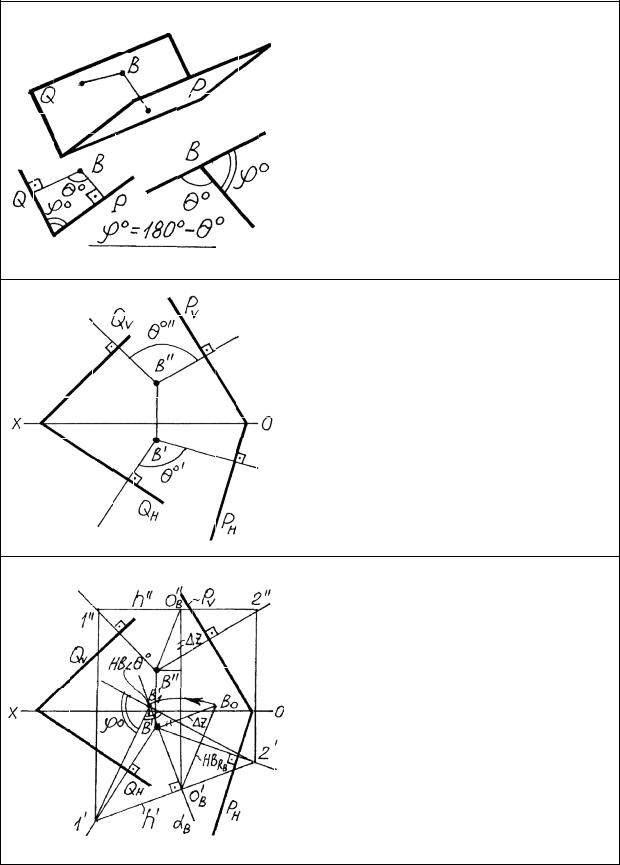
Определение угла между плоскостями
Наиболее эффективным методом определения угла между двумя плоскостями является метод дополнительного угла. Дополнительным углом называется угол между двумя перпендикулярами, опущенными из любой точки на обе плоскости. Искомый и дополнительный углы связаны формулой, которая реализуется графически.
Требуется определить угол между двумя плоскостями. Из любой точки между плоскостями, например В, опустим перпендикуляры на заданные плоскости. Проекции перпендикуляров проводим согласно алгоритму перпендикулярности. Между проекциями перпендикуляров образуются проекции дополнительного угла.
Определим натуральную величину дополнительного угла методом вращения вокруг горизонтали. Объектом вращения будет вершина В угла. Проводим через В/ плоскость вращения, находим центр вращенияО, определяем натуральную величину радиуса вращения Rв и откладываем его вдоль плоскости вращения. Графически находим искомый угол.
45
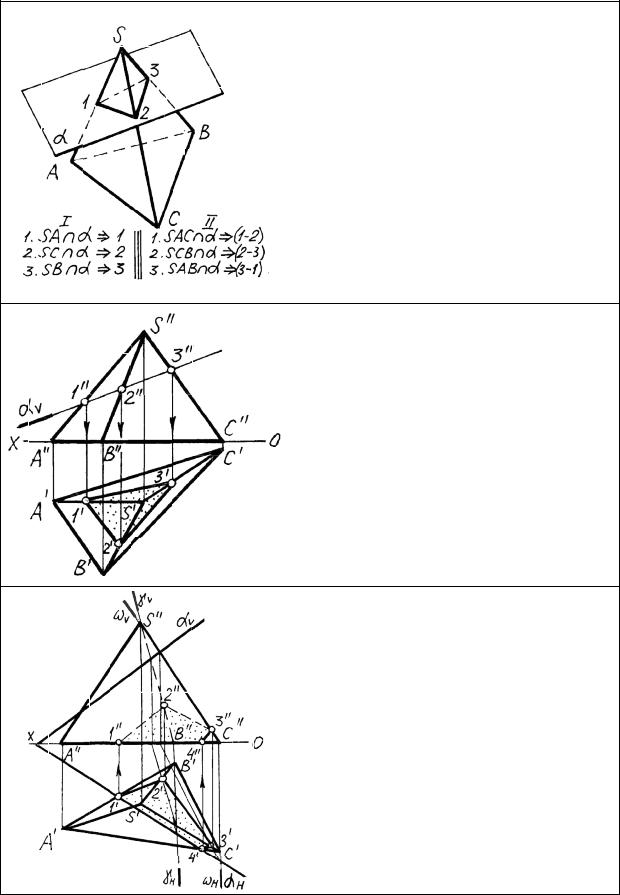
Методы построения сечений многогранников
Разработано два метода построения сечений многогранников – метод ребер и метод граней. В методе ребер находят точки пересечения ребер многогранника с секущей плоскостью, т.е. несколько раз решают типовую задачу о пересечении прямой с плоскостью. В методе граней находят линии пересечения граней многогранника с плоскостью, т.е. решают типовую задачу о -пере сечении плоскостей.
Рассмотрим пересечение пирамиды фронтально-проецирующей плоскостью. Решаем задачу методом ребер. Так как секущая плоскость фрон- тально-проецирующая, то на фронтальной проекции точки пересечения определяются без построений. По линиям связи находим горизонтальные проекции точек, соединив которые получим сечение.
Если секущая плоскость является плоскостью общего положения,то задача усложняется. При построении точек сечения проводим через ребра вспомогательные плоскости частного положения, находим линии пересечения заданной и вспомогательной плоскостей и на пересечении ребер с линиями пересечения находим искомые точки.
46
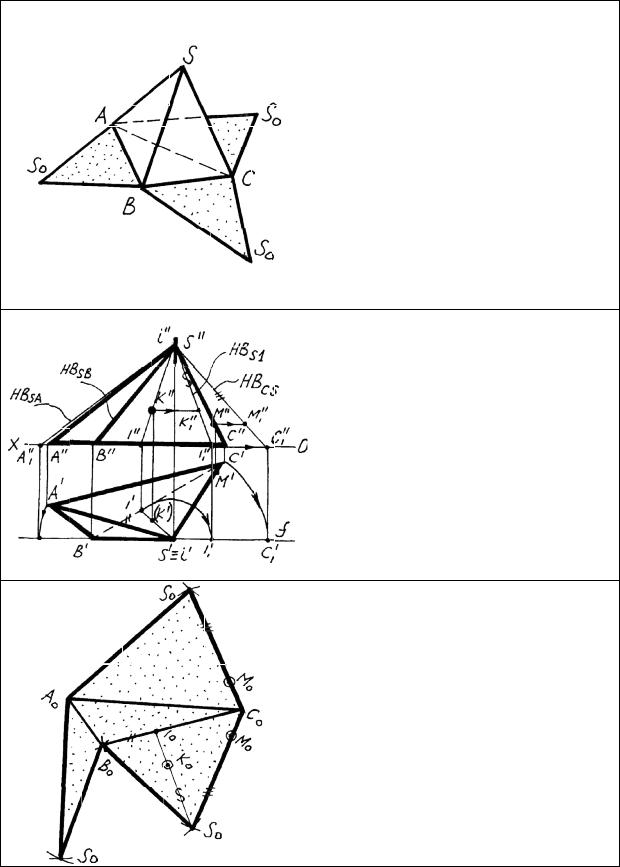
Построение разверток многогранников
При построении разверток многогранников используют два метода: метод раскатки и метод нормального сечения. Наиболее распространен первый метод. Метод раскатки заключается в том, что многогранник условно разрезают по ребрам и «раскатывают» грани в одну плоскость.
Рассмотрим построение развертки пирамиды.
Требуется построить развертку и указать на ней точкиК и М, лежащие на поверхности пирамиды. Сначала определяем натуральную величину ребер методом вращения вокруг оси i. Проекции точки К находим с помощью вспомогательной прямой.
Далее на свободном поле чертежа строим основание пирамиды. К основанию пристраиваем боковые грани пирамиды. Точку К на развертке строим с помощью вспомогательной прямой. Все построения проводятся с помощью циркуля.
47
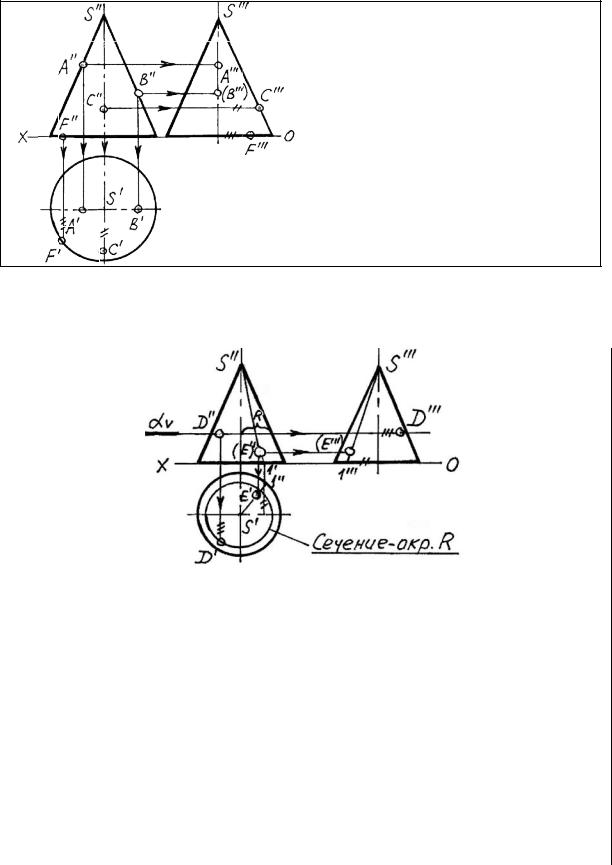
Построение проекций особых точек на поверхности
Особые (характерные) точки – это точки, лежащие на образующих поверхности, основаниях, и точки, совпадающие с осями. При построении проекций характерных точек исполь-
зуется одно из свойств эпюра Монжа : АХА/ = AZA///.
Построение промежуточных точек на поверхности
|
Промежуточные |
точки |
занимают |
общее |
положение |
на |
|
|
поверхности. Их построение связано с определенными трудностями. |
||||||
|
Имеется два способа построения проекций промежуточных точек: |
||||||
|
способ образующих и метод секущих вспомогательных плоскостей. |
||||||
|
Первый метод заключается в том, что через проекцию точки проводят |
||||||
|
образующую линию (прямую), строят ее проекции и на них находят |
||||||
|
проекции точки. |
||||||
|
По второму способу через точку проводят вспомогательную |
||||||
|
плоскость, строят сечение поверхности вспомогательной плоскостью |
||||||
|
и на контуре сечения находят проекцию промежуточной точки. |
||||||
|
Третью проекцию строят с помощью упомянутого свойства эпюра |
||||||
|
Монжа. В качестве вспомогательных плоскостей применяют плос- |
||||||
|
кости, которые образуют простые сечения поверхностей. |
48
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
