8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между плоскостями (двугранный угол)
(blacktriangleright) Двугранный угол – угол, образованный двумя полуплоскостями и прямой (a), которая является их общей границей.
(blacktriangleright) Чтобы найти угол между плоскостями (xi) и (pi), нужно найти линейный угол (причем острый или прямой) двугранного угла, образованного плоскостями (xi) и (pi):
Шаг 1: пусть (xicappi=a) (линия пересечения плоскостей). В плоскости (xi) отметим произвольную точку (F) и проведем (FAperp
a);
Шаг 2: проведем (FGperp pi);
Шаг 3: по ТТП ((FG) – перпендикуляр, (FA) –наклонная, (AG) – проекция) имеем: (AGperp a);
Шаг 4: угол (angle FAG) называется линейным углом двугранного угла, образованного плоскостями (xi) и (pi).
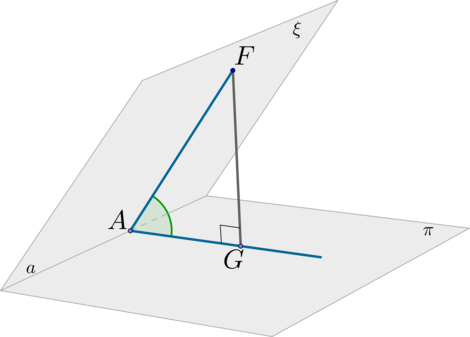
Заметим, что треугольник (AG) – прямоугольный.
Заметим также, что плоскость (AFG), построенная таким образом, перпендикулярна обеим плоскостям (xi) и (pi). Следовательно, можно сказать по-другому: угол между плоскостями (xi) и (pi) — это угол между двумя пересекающимися прямыми (cin xi) и (binpi), образующими плоскость, перпендикулярную и (xi), и (pi).
Задание
1
#2875
Уровень задания: Сложнее ЕГЭ
Дана четырехугольная пирамида, все ребра которой равны, причем основание является квадратом. Найдите (6cos alpha), где (alpha) – угол между ее смежными боковыми гранями.
Пусть (SABCD) – данная пирамида ((S) – вершина), ребра которой равны (a). Следовательно, все боковые грани представляют собой равные равносторонние треугольники. Найдем угол между гранями (SAD) и (SCD).
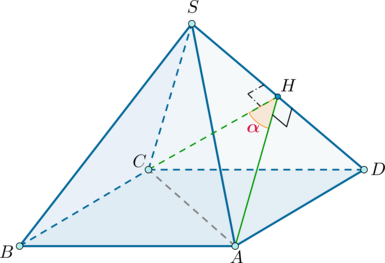
Проведем (CHperp SD). Так как (triangle SAD=triangle SCD), то (AH) также будет высотой в (triangle SAD). Следовательно, по определению (angle AHC=alpha) – линейный угол двугранного угла между гранями (SAD) и (SCD).
Так как в основании лежит квадрат, то (AC=asqrt2). Заметим также, что (CH=AH) – высота равностороннего треугольника со стороной (a), следовательно, (CH=AH=frac{sqrt3}2a).
Тогда по теореме косинусов из (triangle AHC): [cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH}=-dfrac13 quadRightarrowquad
6cosalpha=-2.]
Ответ: -2
Задание
2
#2876
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются под углом, косинус которого равен (0,2). Плоскости (pi_2) и (pi_3) пересекаются под прямым углом, причем линия пересечения плоскостей (pi_1) и (pi_2) параллельна линии пересечения плоскостей (pi_2) и (pi_3). Найдите синус угла между плоскостями (pi_1) и (pi_3).
Пусть линия пересечения (pi_1) и (pi_2) – прямая (a), линия пересечения (pi_2) и (pi_3) – прямая (b), а линия пересечения (pi_3) и (pi_1) – прямая (c). Так как (aparallel b), то (cparallel aparallel b) (по теореме из раздела теоретической справки “Геометрия в пространстве” (rightarrow) “Введение в стереометрию, параллельность”).
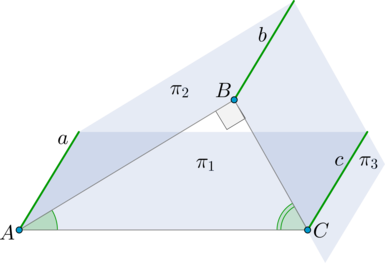
Отметим точки (Ain a, Bin b) так, чтобы (ABperp a, ABperp b) (это возможно, так как (aparallel b)). Отметим (Cin c) так, чтобы (BCperp c), следовательно, (BCperp b). Тогда (ACperp c) и (ACperp a).
Действительно, так как (ABperp b, BCperp b), то (b) перпендикулярна плоскости (ABC). Так как (cparallel aparallel b), то прямые (a) и (c) тоже перпендикулярны плоскости (ABC), а значит и любой прямой из этой плоскости, в частности, прямой (AC).
Отсюда следует, что (angle BAC=angle (pi_1, pi_2)), (angle
ABC=angle (pi_2, pi_3)=90^circ), (angle BCA=angle (pi_3,
pi_1)). Получается, что (triangle ABC) прямоугольный, а значит [sin angle BCA=cos angle BAC=0,2.]
Ответ: 0,2
Задание
3
#2877
Уровень задания: Сложнее ЕГЭ
Даны прямые (a, b, c), пересекающиеся в одной точке, причем угол между любыми двумя из них равен (60^circ). Найдите (cos^{-1}alpha), где (alpha) – угол между плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Ответ дайте в градусах.
Пусть прямые пересекаются в точке (O). Так как угол между любыми двумя их них равен (60^circ), то все три прямые не могут лежать в одной плоскости. Отметим на прямой (a) точку (A) и проведем (ABperp
b) и (ACperp c). Тогда (triangle AOB=triangle AOC) как прямоугольные по гипотенузе и острому углу. Следовательно, (OB=OC) и (AB=AC).
Проведем (AHperp (BOC)). Тогда по теореме о трех перпендикулярах (HCperp c), (HBperp b). Так как (AB=AC), то (triangle
AHB=triangle AHC) как прямоугольные по гипотенузе и катету. Следовательно, (HB=HC). Значит, (OH) – биссектриса угла (BOC) (так как точка (H) равноудалена от сторон угла).
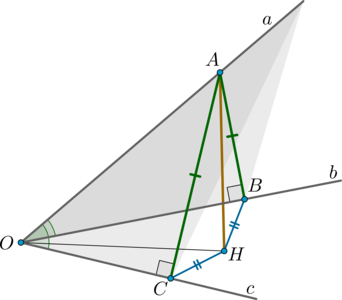
Заметим, что таким образом мы к тому же построили линейный угол двугранного угла, образованного плоскостью, образованной прямыми (a) и (c), и плоскостью, образованной прямыми (b) и (c). Это угол (ACH).
Найдем этот угол. Так как точку (A) мы выбирали произвольно, то пусть мы выбрали ее так, что (OA=2). Тогда в прямоугольном (triangle AOC): [sin 60^circ=dfrac{AC}{OA}
quadRightarrowquad AC=sqrt3 quadRightarrowquad
OC=sqrt{OA^2-AC^2}=1.] Так как (OH) – биссектриса, то (angle
HOC=30^circ), следовательно, в прямоугольном (triangle HOC): [mathrm{tg},30^circ=dfrac{HC}{OC}quadRightarrowquad HC=dfrac1{sqrt3}.] Тогда из прямоугольного (triangle ACH): [cosangle alpha=cosangle ACH=dfrac{HC}{AC}=dfrac13 quadRightarrowquad
cos^{-1}alpha=3.]
Ответ: 3
Задание
4
#2910
Уровень задания: Сложнее ЕГЭ
Плоскости (pi_1) и (pi_2) пересекаются по прямой (l), на которой лежат точки (M) и (N). Отрезки (MA) и (MB) перпендикулярны прямой (l) и лежат в плоскостях (pi_1) и (pi_2) соответственно, причем (MN = 15), (AN = 39), (BN = 17), (AB = 40). Найдите (3cosalpha), где (alpha) – угол между плоскостями (pi_1) и (pi_2).
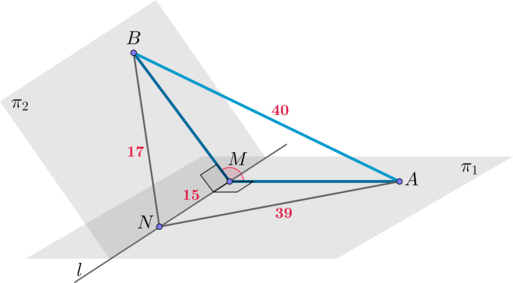
Треугольник (AMN) прямоугольный, (AN^2 = AM^2 + MN^2), откуда [AM^2 = 39^2 – 15^2 = 36^2.] Треугольник (BMN) прямоугольный, (BN^2 = BM^2 + MN^2), откуда [BM^2 = 17^2 – 15^2 = 8^2.] Запишем для треугольника (AMB) теорему косинусов: [AB^2 = AM^2 + MB^2 – 2cdot AMcdot MBcdotcosangle AMB.] Тогда [40^2 = 36^2 + 8^2 – 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12}] Так как угол (alpha) между плоскостями – это острый угол, а (angle AMB) получился тупым, то (cosalpha=dfrac5{12}). Тогда [3cosalpha = dfrac54=1,25.]
Ответ: 1,25
Задание
5
#2911
Уровень задания: Сложнее ЕГЭ
(ABCDA_1B_1C_1D_1) – параллелепипед, (ABCD) – квадрат со стороной (a), точка (M) – основание перпендикуляра, опущенного из точки (A_1) на плоскость ((ABCD)), кроме того (M) – точка пересечения диагоналей квадрата (ABCD). Известно, что (A_1M = dfrac{sqrt{3}}{2}a). Найдите угол между плоскостями ((ABCD)) и ((AA_1B_1B)). Ответ дайте в градусах.
Построим (MN) перпендикулярно (AB) как показано на рисунке.
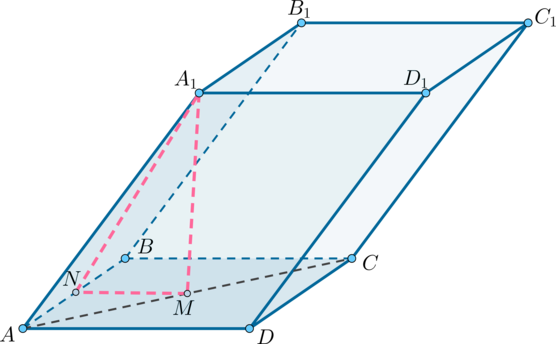
Так как (ABCD) – квадрат со стороной (a) и (MNperp AB) и (BCperp AB), то (MNparallel BC). Так как (M) – точка пересечения диагоналей квадрата, то (M) – середина (AC), следовательно, (MN) – средняя линия и (MN =frac12BC= frac{1}{2}a).
(MN) – проекция (A_1N) на плоскость ((ABCD)), причем (MN) перпендикулярен (AB), тогда по теореме о трех перпендикулярах (A_1N) перпендикулярен (AB) и угол между плоскостями ((ABCD)) и ((AA_1B_1B)) есть (angle A_1NM).
[mathrm{tg}, angle A_1NM = dfrac{A_1M}{NM} = dfrac{frac{sqrt{3}}{2}a}{frac{1}{2}a} = sqrt{3}qquadRightarrowqquadangle A_1NM = 60^{circ}]
Ответ: 60
Задание
6
#1854
Уровень задания: Сложнее ЕГЭ
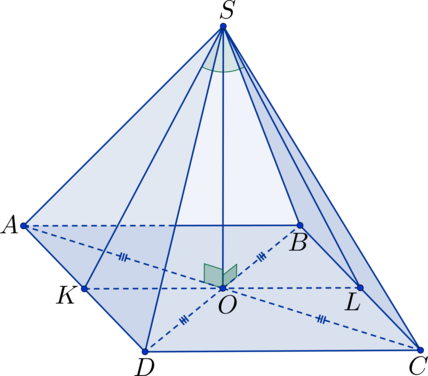
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (ABC), если (SO = 5), а (AB = 10).
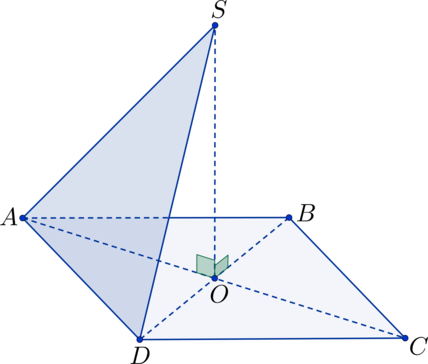
Прямоугольные треугольники (triangle SAO) и (triangle SDO) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = 90^circ); (AO = DO), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = SD) (Rightarrow) (triangle ASD) – равнобедренный. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскостям (ASD) и (ABC) (Rightarrow) (angle SKO) – линейный угол, равный искомому двугранному углу.
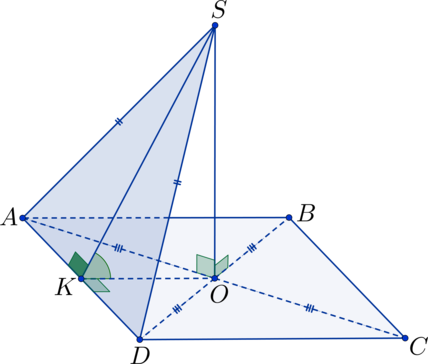
В (triangle SKO): (OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO) (Rightarrow) (triangle SOK) – равнобедренный прямоугольный треугольник (Rightarrow) (angle SKO = 45^circ).
Ответ: 45
Задание
7
#1855
Уровень задания: Сложнее ЕГЭ
В квадрате (ABCD): (O) – точка пересечения диагоналей; (S) – не лежит в плоскости квадрата, (SO perp ABC). Найдите угол между плоскостями (ASD) и (BSC), если (SO = 5), а (AB = 10).
Прямоугольные треугольники (triangle SAO), (triangle SDO), (triangle SOB) и (triangle SOC) равны по двум сторонам и углу между ними ((SO perp ABC) (Rightarrow) (angle SOA = angle SOD = angle SOB = angle SOC = 90^circ); (AO = OD = OB = OC), т.к. (O) – точка пересечения диагоналей квадрата, (SO) – общая сторона) (Rightarrow) (AS = DS = BS = CS) (Rightarrow) (triangle ASD) и (triangle BSC) – равнобедренные. Точка (K) – середина (AD), тогда (SK) – высота в треугольнике (triangle ASD), а (OK) – высота в треугольнике (AOD) (Rightarrow) плоскость (SOK) перпендикулярна плоскости (ASD). Точка (L) – середина (BC), тогда (SL) – высота в треугольнике (triangle BSC), а (OL) – высота в треугольнике (BOC) (Rightarrow) плоскость (SOL) (она же плоскость (SOK)) перпендикулярна плоскости (BSC). Таким образом получаем, что (angle KSL) – линейный угол, равный искомому двугранному углу.
(KL = KO + OL = 2cdot OL = AB = 10) (Rightarrow) (OL = 5); (SK = SL) – высоты в равных равнобедренных треугольниках, которые можно найти по теореме Пифагора: (SL^2 = SO^2 + OL^2 = 5^2 + 5^2 = 50). Можно заметить, что (SK^2 + SL^2 = 50 + 50 = 100 = KL^2) (Rightarrow) для треугольника (triangle KSL) выполняется обратная теорема Пифагора (Rightarrow) (triangle KSL) – прямоугольный треугольник (Rightarrow) (angle KSL = 90^circ).
Ответ: 90
Подготовка учащихся к сдаче ЕГЭ по математике, как правило, начинается с повторения основных формул, в том числе и тех, которые позволяют определить угол между плоскостями. Несмотря на то, что этот раздел геометрии достаточно подробно освещается в рамках школьной программы, многие выпускники нуждаются в повторении базового материала. Понимая, как найти угол между плоскостями, старшеклассники смогут оперативно вычислить правильный ответ в ходе решения задачи и рассчитывать на получение достойных баллов по итогам сдачи единого государственного экзамена.
Основные нюансы
-
Чтобы вопрос, как найти двугранный угол, не вызывал затруднений, рекомендуем следовать алгоритму решения, который поможет справиться с заданиями ЕГЭ.
-
Вначале необходимо определить прямую, по которой пересекаются плоскости.
-
Затем на этой прямой нужно выбрать точку и провести к ней два перпендикуляра.
-
Следующий шаг — нахождение тригонометрической функции двугранного угла, который образован перпендикулярами. Делать это удобнее всего при помощи получившегося треугольника, частью которого является угол.
-
Ответом будет значение угла или его тригонометрической функции.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха
В процессе занятий накануне сдачи ЕГЭ многие школьники сталкиваются с проблемой поиска определений и формул, которые позволяют вычислить угол между 2 плоскостями. Школьный учебник не всегда есть под рукой именно тогда, когда это необходимо. А чтобы найти нужные формулы и примеры их правильного применения, в том числе и для нахождения угла между плоскостями в Интернете в режиме онлайн, порой требуется потратить немало времени.
Математический портал «Школково» предлагает новый подход к подготовке к госэкзамену. Занятия на нашем сайте помогут ученикам определить наиболее сложные для себя разделы и восполнить пробелы в знаниях.
Мы подготовили и понятно изложили весь необходимый материал. Базовые определения и формулы представлены в разделе «Теоретическая справка».
Для того чтобы лучше усвоить материал, предлагаем также попрактиковаться в выполнении соответствующих упражнений. Большая подборка задач различной степени сложности, например, на нахождение угла между прямой и плоскостью, представлена в разделе «Каталог». Все задания содержат подробный алгоритм нахождения правильного ответа. Перечень упражнений на сайте постоянно дополняется и обновляется.
Практикуясь в решении задач, в которых требуется найти угол между двумя плоскостями, учащиеся имеют возможность в онлайн-режиме сохранить любое задание в «Избранное». Благодаря этому они смогут вернуться к нему необходимое количество раз и обсудить ход его решения со школьным учителем или репетитором.

УСТАЛ? Просто отдохни
Здравствуйте, дорогие подписчики и гости канала. Сегодня разбираем 13 задачу с сайта РЕШУ ЕГЭ
Вот условие задачи
Первое легко доказывается с помощью теоремы о трех перпендикулярах:
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной
Теперь зная, что А1Н перпендикурно BD легко найти угол между плоскостями – это угол между перпендикулярами, проведенными к линии пересечения плоскостей, то есть угол между А1Н и АН
Рассмотрим прямоугольный треугольник АА1Н
Найдем тангенс угла А1АН:
Спасибо за внимание
Буду рада вашим лайкам, комментариям и вашей подписке
Также приглашаю на канал в
Телеграм и в группу Вконтакте
До новых встреч на канале Простаяматематика.рф
Как найти угол между двумя плоскостями?
Пусть заданы уравнениями две плоскости $$A_1 x + B_1 y + C_1 z + D_1 = 0$$ $$A_2 x + B_2 y + C_2 z + D_2 = 0$$
Запишем нормальные векторы этих плоскостей, каждая координата которых равна соответствующим коэффициентам в уравнениях плоскостей $$overline{n}_1 = (A_1,B_1,C_1)$$$$overline{n}_2 = (A_2,B_2,C_2)$$
Угол между плоскостями – это угол между двумя нормальными векторами этих плоскостей, вычисляемый по формуле: $$cos varphi = frac{(overline{n}_1,overline{n}_2)}{|overline{n}_2| cdot |overline{n}_2|}$$
В числителе формулы стоит скалярное произведение векторов, вычисляемое путем суммирования произведений соответствующих координат
$$(overline{n}_1,overline{n}_2) = A_1 cdot A_2 + B_1 cdot B_2 + C_1 cdot C_2$$
В знаменателе расположено произведение длин векторов, вычисляемых извлечением квадратного корня из суммы квадратов соответствующих координат векторов
$$|overline{n}_1| = sqrt{A_1 ^2 + B_1 ^2 + C_1 ^2}$$
$$|overline{n}_2| = sqrt{A_2 ^2 + B_2 ^2 + C_2 ^2}$$
- Вычисляем скалярное произведение нормальных векторов $(overline{n}_1,overline{n}_2)$
- Находим произведение модулей нормальных векторов $ |overline{n}_1| cdot |overline{n}_2| $
- Подставляем найденные значения в формулу косинуса угла между плоскостями $ cos varphi $
Примеры решений
| Пример 1 |
| Найти угол между плоскостями $3x-y+3=0$ и $x-2y+5z-10=0$ |
| Решение |
|
Записываем нормальные векторы каждой из плоскостей. В качестве координат векторов подставляем коэффициенты из уравнений плоскостей $$ overline{n}_1 = (3,-1,0) $$ $$ overline{n}_2 = (1,-2,5) $$ Вычисляем скалярное произведение, полученных векторов $overline{n}_1$ и $ overline{n}_2$. Выполняем сложение произведений соответствующих координат $$(overline{n}_1,overline{n}_2) = 3cdot 1 + (-1)cdot (-2) + 0cdot 5 = 5$$ Находим модули каждого из векторов. Извлекаем квадратный корень из суммы квадратов соответствующих координат $$|overline{n}_1| = sqrt{3^2 + (-1)^2 + 0^2} = sqrt{10}$$ $$|overline{n}_2| = sqrt{1^2+(-2)^2+5^2} = sqrt{30}$$ Подставляем полученные значения в формулу нахождения угла между плоскостями $$cos varphi = frac{5}{sqrt{10} cdot sqrt{30}} = frac{1}{sqrt{12}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$varphi = arccosfrac{1}{sqrt{12}}$$ |
19
Мар 2012
13 Задание (2022) (C2)ВИДЕОУРОКИ
Угол между плоскостями. Метод координат. Задание 14
Угол между плоскостями. Метод координант.
В этой статье я расскажу, как решать задачи на нахождение угла между плоскостями с помощью метода координат.
Сначала немного теории.
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величина двугранного угла измеряется величиной соответствующего линейного угла.
Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:

Пусть наши плоскости ![]() и
и ![]() заданы уравнениями:
заданы уравнениями:
![]() :
: ![]()
![]() :
: ![]()
Косинус угла ![]() между плоскостями находится по такой формуле:
между плоскостями находится по такой формуле:
![]()
В ответе мы записываем ![]() , так как величиной угла между плоскостями называется величина меньшего двугранного угла.
, так как величиной угла между плоскостями называется величина меньшего двугранного угла.
Решим задачу, которая была предложена на пробнике для подготовке к ЕГЭ 17 марта 2012 года.
В правильной четырехугольной призме ![]() со стороной основания 12 и высотой 21 на ребре
со стороной основания 12 и высотой 21 на ребре ![]() взята точка М так, что
взята точка М так, что ![]() . На ребре
. На ребре ![]() взята точка K так, что
взята точка K так, что ![]() . Найдите угол между плоскостью
. Найдите угол между плоскостью ![]() и плоскостью
и плоскостью ![]() .
.
Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат:
Теперь перед нами стоит задача написать уравнения плоскости ![]() и плоскости
и плоскости ![]()
Подробный алгоритм нахождения уравнения плоскости ![]() по трем точкам я описывала здесь.
по трем точкам я описывала здесь.
После того, как мы найдем коэффициенты в уравнениях плоскости ![]() и плоскости
и плоскости ![]() , подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.
, подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.
Предлагаю вам посмотреть подробное видеорешение этой задачи:

КУПИТЬ видеокурс “Векторы и координаты. Часть В и Задание 14”
И.В. Фельдман, репетитор по математике.

|
Отзывов (50)
| Метки: решение задания С2
Тема 13.
Задачи по стереометрии
13
.
16
Угол между плоскостями
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
задачи по стереометрии
Решаем задачи
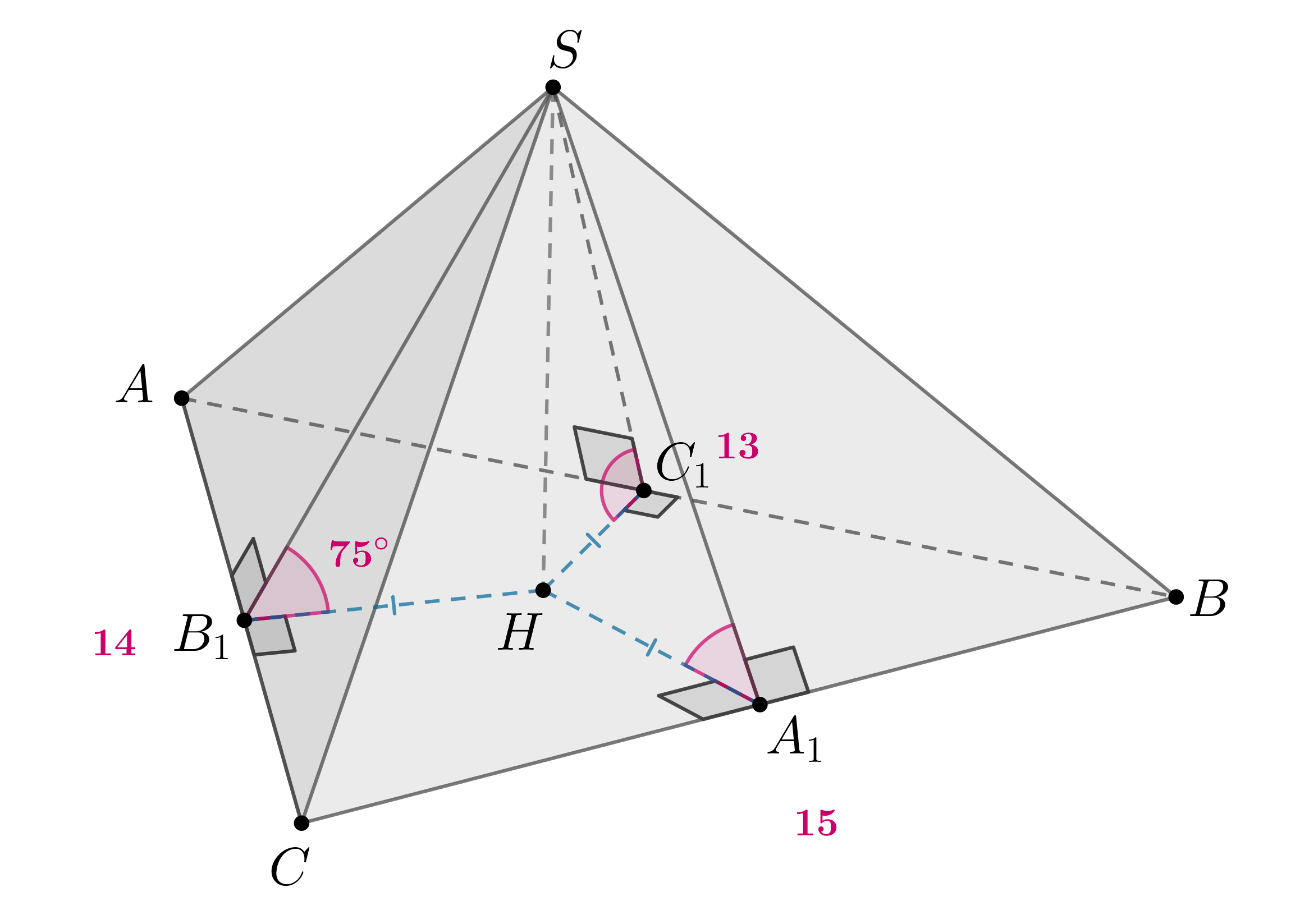
Основание пирамиды — равнобедренный прямоугольный треугольник. Каждый из
двугранных углов при основании равен Высота пирамиды равна
. Найдите
площадь основания.
Показать ответ и решение
Ответ:
Основание пирамиды — треугольник со сторонами 13, 14 и 15. Все двугранные
углы при сторонах основания равны Найдите высоту пирамиды.
Показать ответ и решение
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми
углами, то основание высоты пирамиды — центр вписанной в основание пирамиды
окружности. Докажем это.
Опустим высоту пирамиды
к основанию
Опустим
перпендикуляры
на стороны
По теореме о трех
перпендикулярах отрезки
перпендикулярны сторонам
треугольника
Тогда по определению — линейные углы
двугранных углов, образуемых боковыми гранями пирамиды и ее основанием.
Следовательно, по общему катету и острому углу
Следовательно, Таким образом, точка
— центр
вписанной в окружности радиуса
Будем искать по формуле
Площадь равна
Тогда
Так как то найдем
Следовательно,
Ответ:
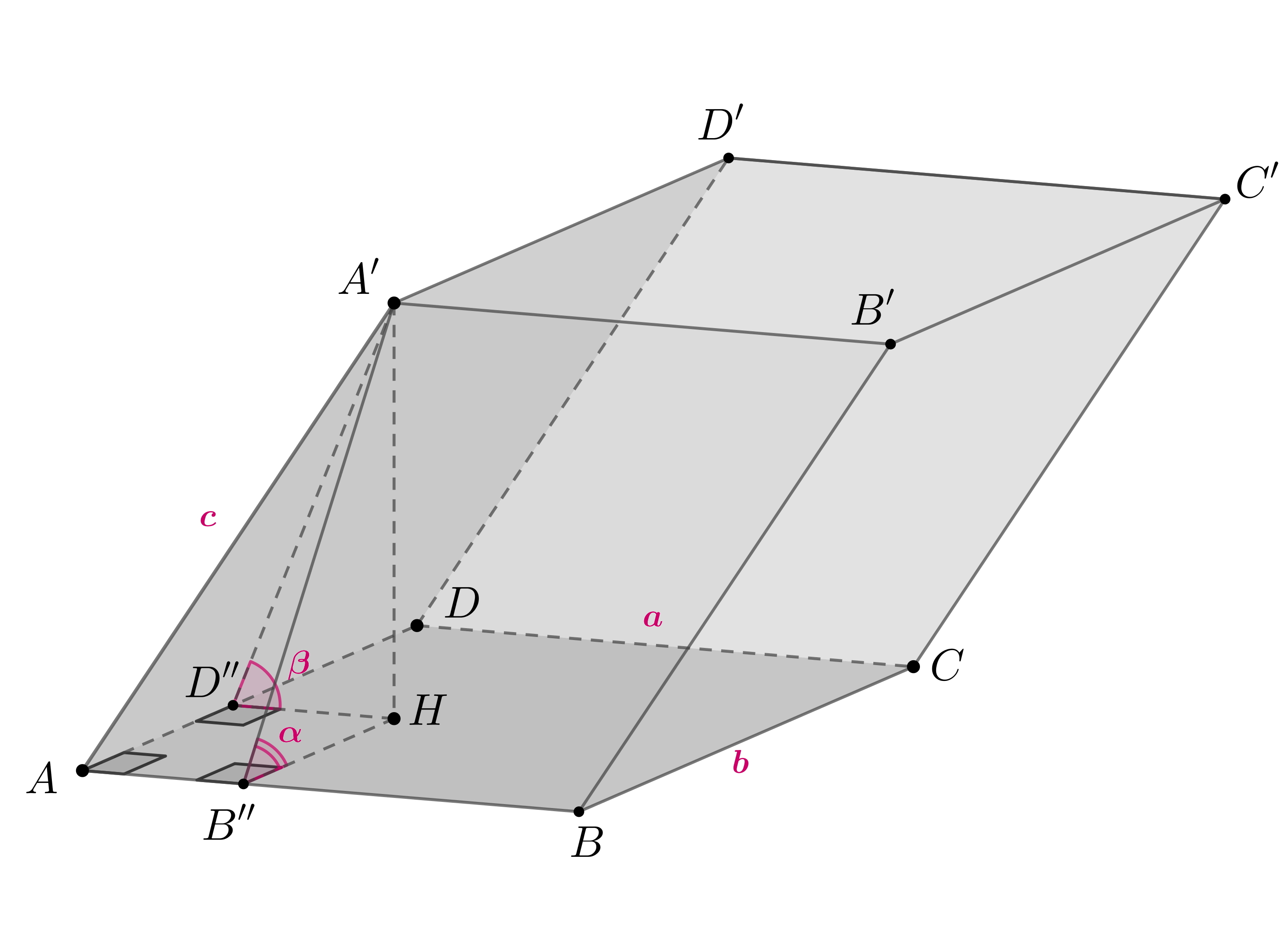
Основанием пирамиды служит треугольник со сторонами 10, 10 и 12. Все боковые
грани пирамиды наклонены к плоскости основания под углом Найдите
высоту пирамиды.
Показать ответ и решение
Ответ:
Показать ответ и решение
Пусть Проведем
Тогда по ТТП
Следовательно, по определению
— линейные углы двугранных углов между боковыми гранями и
основанием.
Пусть
— четырехугольник, три угла которого прямые,
следовательно, это прямоугольник. Таким образом,
Так как , то
Следовательно,
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Проведем Тогда по теореме о трех перпендикулярах наклонная
Следовательно,
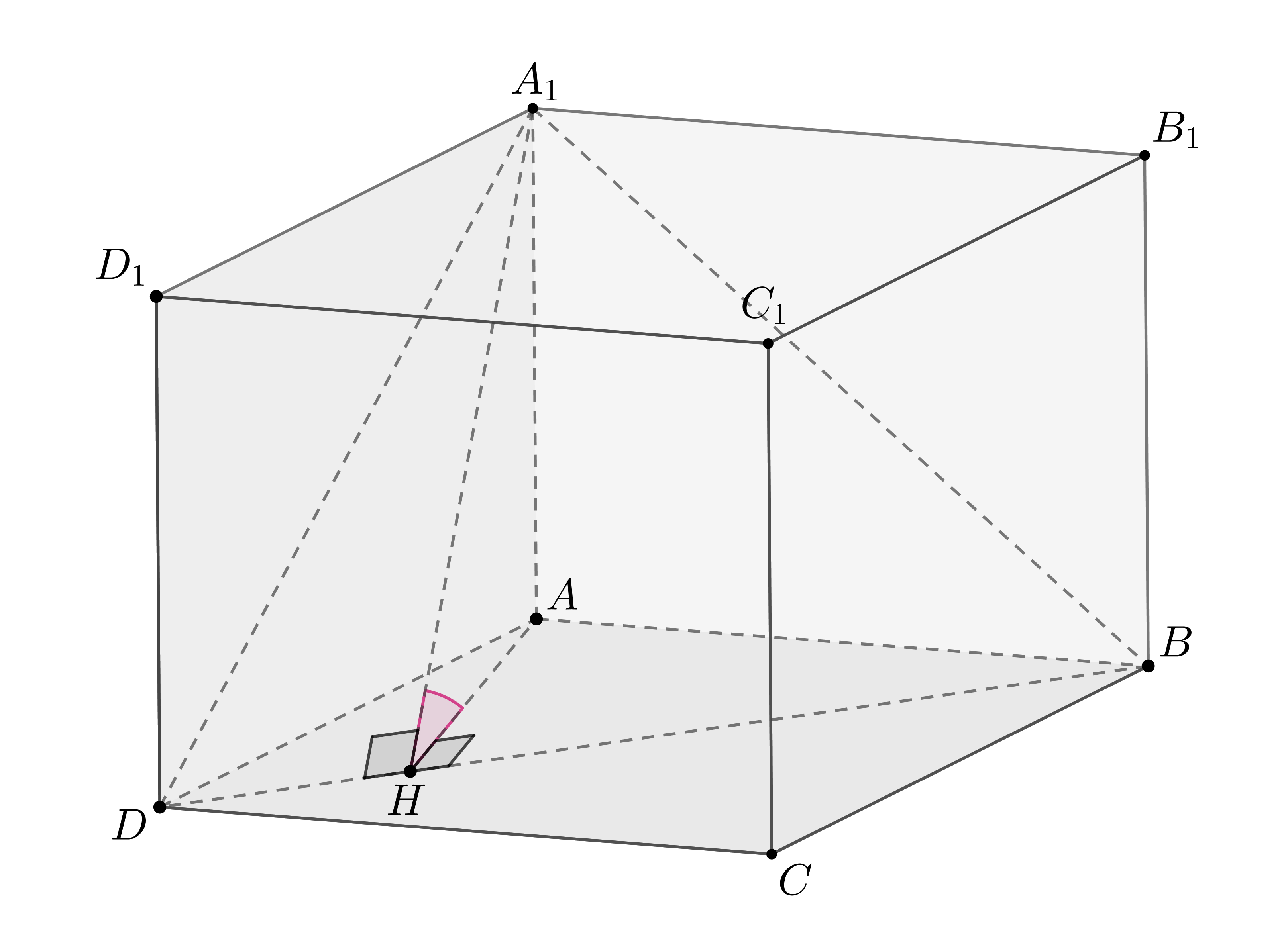
По теореме Пифагора в треугольнике имеем:
Так как то
Тогда
Ответ:
Докажите, что плоскость, делящая пополам двугранный угол при ребре тетраэдра,
делит противоположное ребро на части, пропорциональные площадям граней,
заключающих этот угол.
Показать ответ и решение
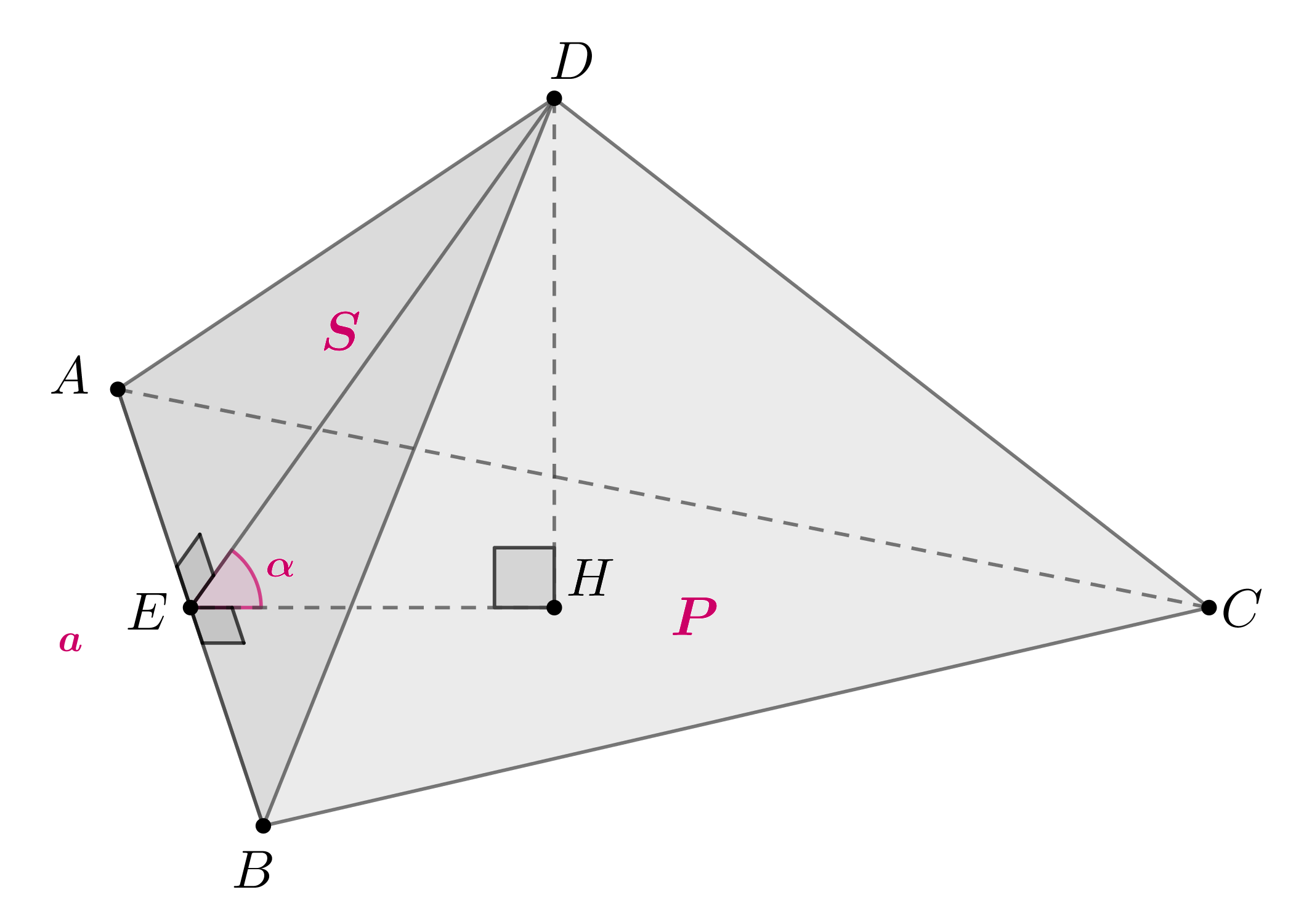
— высота тетраэдра, проведенная к грани площадью
,
,
, тогда по ТТП наклонная
, следовательно,
. Так
как , то
. Из прямоугольного
имеем
, следовательно,
Мы рассмотрели случай, когда . В случай, если
, точка
находится вне грани и работать мы будем с тем же треугольником
,
но с его углом , синус которого равен синусу угла
. Следовательно,
формула останется прежней.
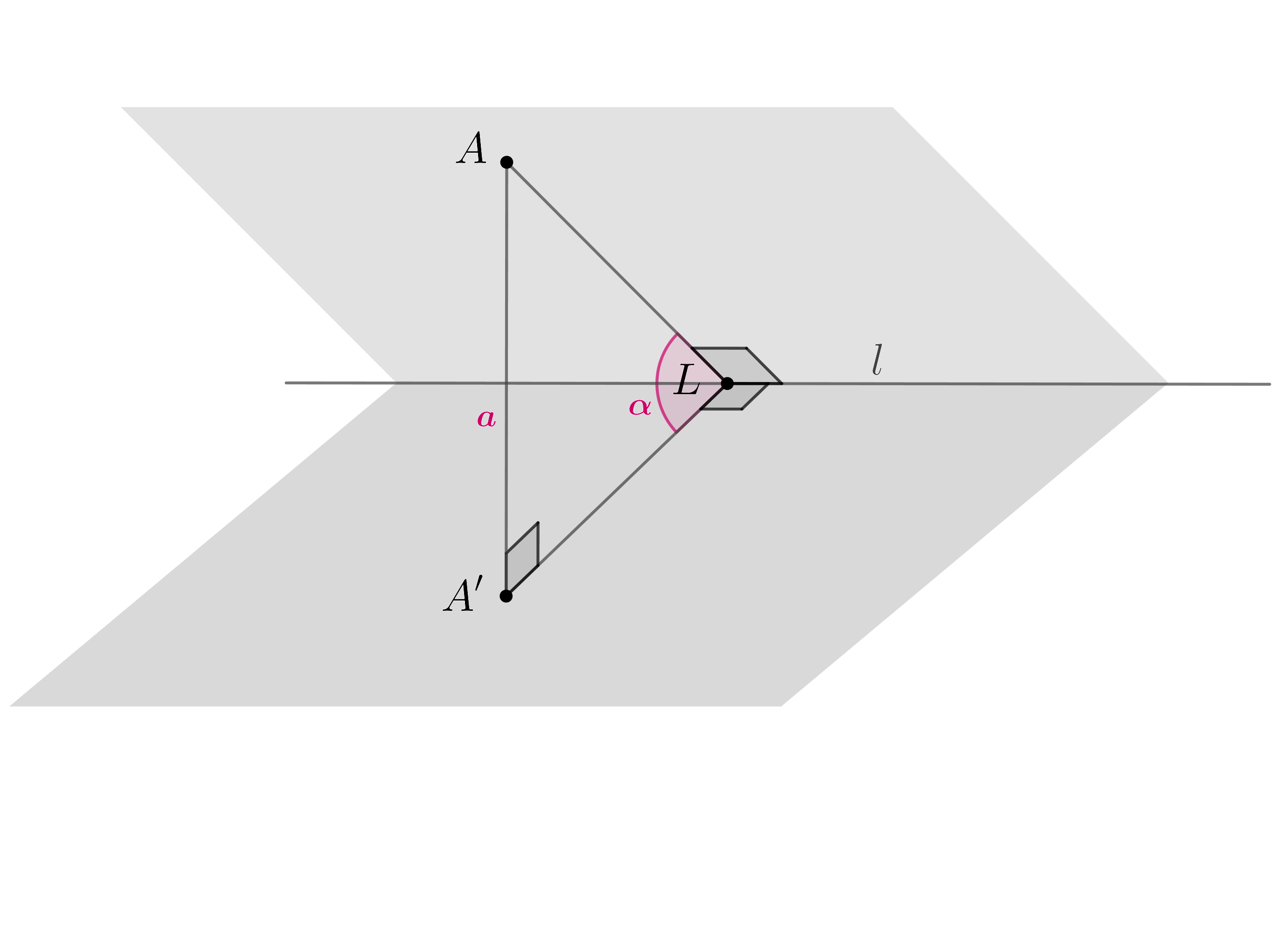
Показать ответ и решение

— линия пересечения плоскостей
и
. Следовательно, так как
,
— линейный угол двугранного угла
между этими плоскостями. Если он острый или прямой, то он равен углу между
этими плоскостями, если он тупой, то смежный с ним угол равен углу между этими
плоскостями, следовательно, угол между и
равен
, если
, и
, если
.
Показать ответ и решение
— перпендикуляр к плоскости, содержащей точку
. Проведем
,
тогда по ТТП наклонная . Следовательно,
— линейный
угол двугранного угла между двумя плоскостями, то есть .
Тогда
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Ответ:
Показать ответ и решение
Проведем через точку прямые параллельно прямым
и
и
переобозначим точки. Пусть эти прямые пересекают ребра и
в точках
и
соответственно, как показано на рисунке. Тогда
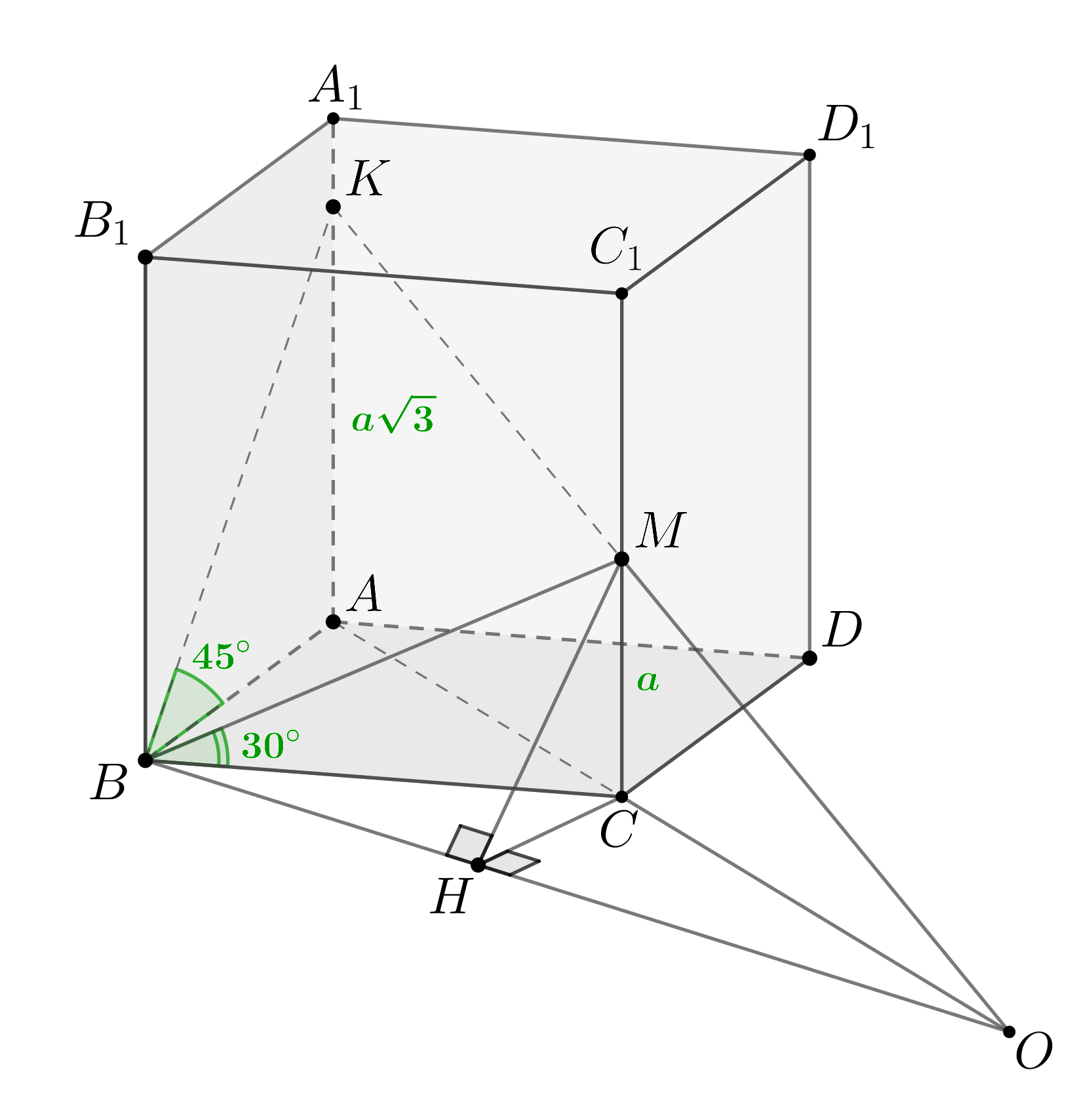
Построим линейный угол двугранного угла, образуемого плоскостями
и Для этого нужно найти линию пересечения этих плоскостей.
Пусть тогда
— линия пересечения плоскостей
и
Проведем
Тогда по ТТП
Следовательно,
— искомый линейный угол.
Пусть Тогда
следовательно,
Так как то
, следовательно,
правильный,
то есть

Из подобия имеем:
Тогда
По теореме косинусов для
По теореме синусов для этого же треугольника:
Из имеем:
Следовательно, из
Ответ:
Показать ответ и решение
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то . Следовательно,
— двугранный угол при
боковом ребре пирамиды.
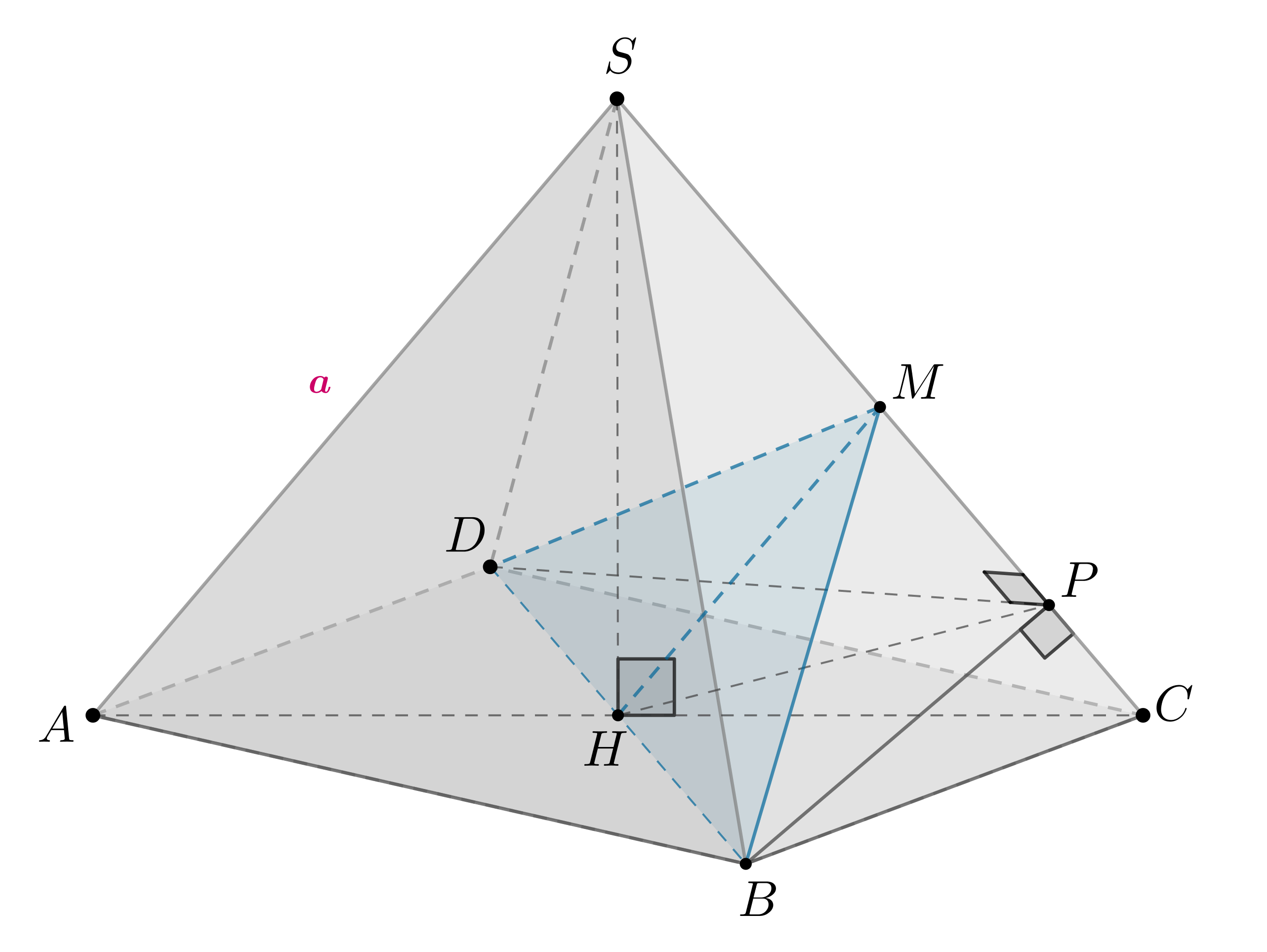
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника , проведенная к гипотенузе. Введем
. Так как
.
— проекция
на плоскость
. Так как
по
ТТП
Так как
— медиана
прямоугольного треугольника, проведенная к гипотенузе, то
Ответ:
Найдите объем правильной четырехугольной пирамиды с высотой и
двугранным углом при боковом ребре.
Показать ответ и решение
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то . Следовательно,
— двугранный угол при
боковом ребре пирамиды. Введем .
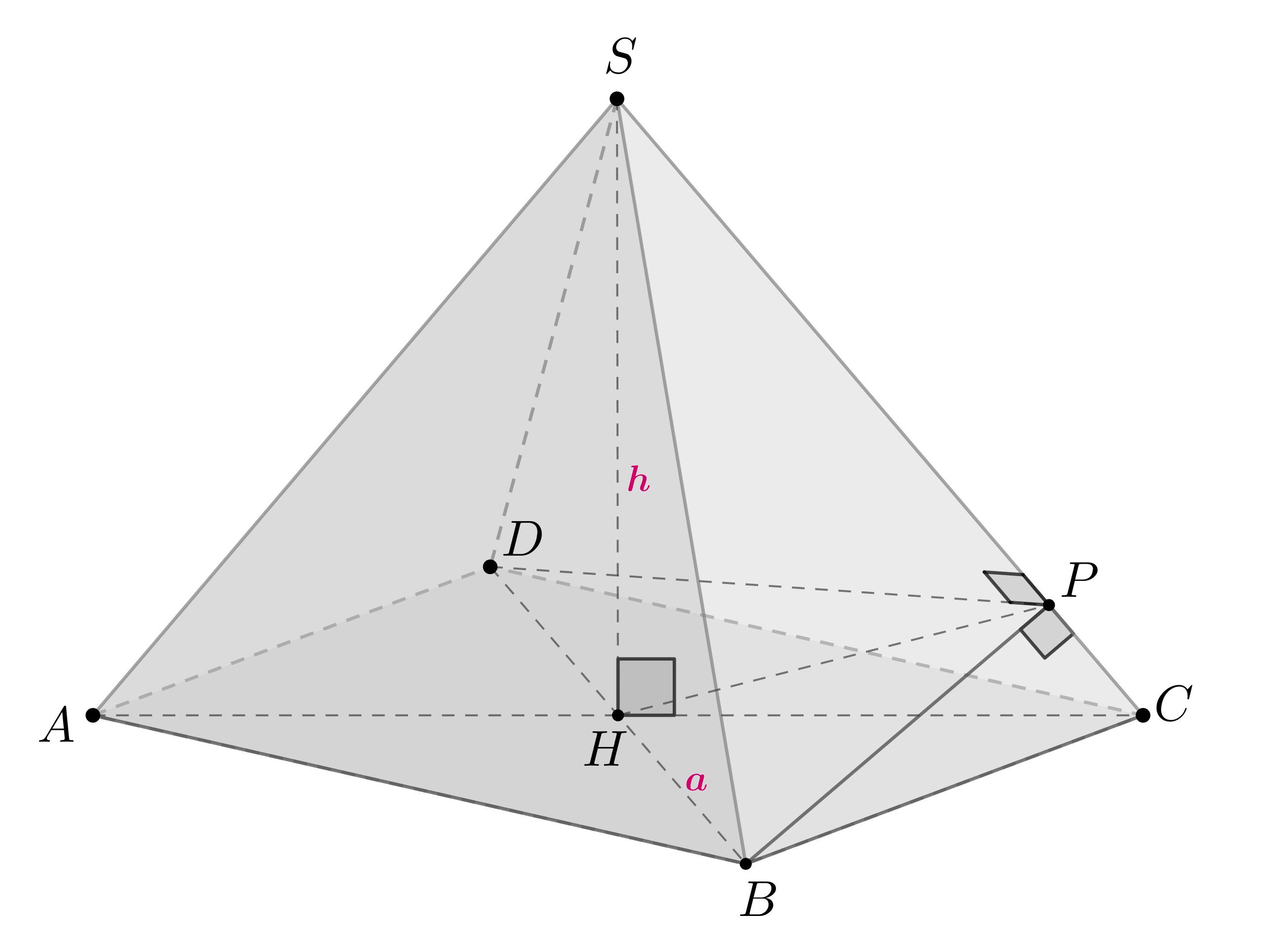
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника , проведенная к гипотенузе. Так как
.
Так как , то
, следовательно,
Ответ:
Показать ответ и решение
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми
углами (двугранные углы при ребрах основания равны), то основание высоты
пирамиды — центр вписанной в основание окружности. Докажем это.
Проведем ,
,
. Тогда по ТТП
,
,
. Следовательно,
—
двугранные углы при ребрах основания пирамиды. Следовательно,
как прямоугольные по катету и острому углу.
Отсюда , то есть
— центр вписанной в
окружности радиуса
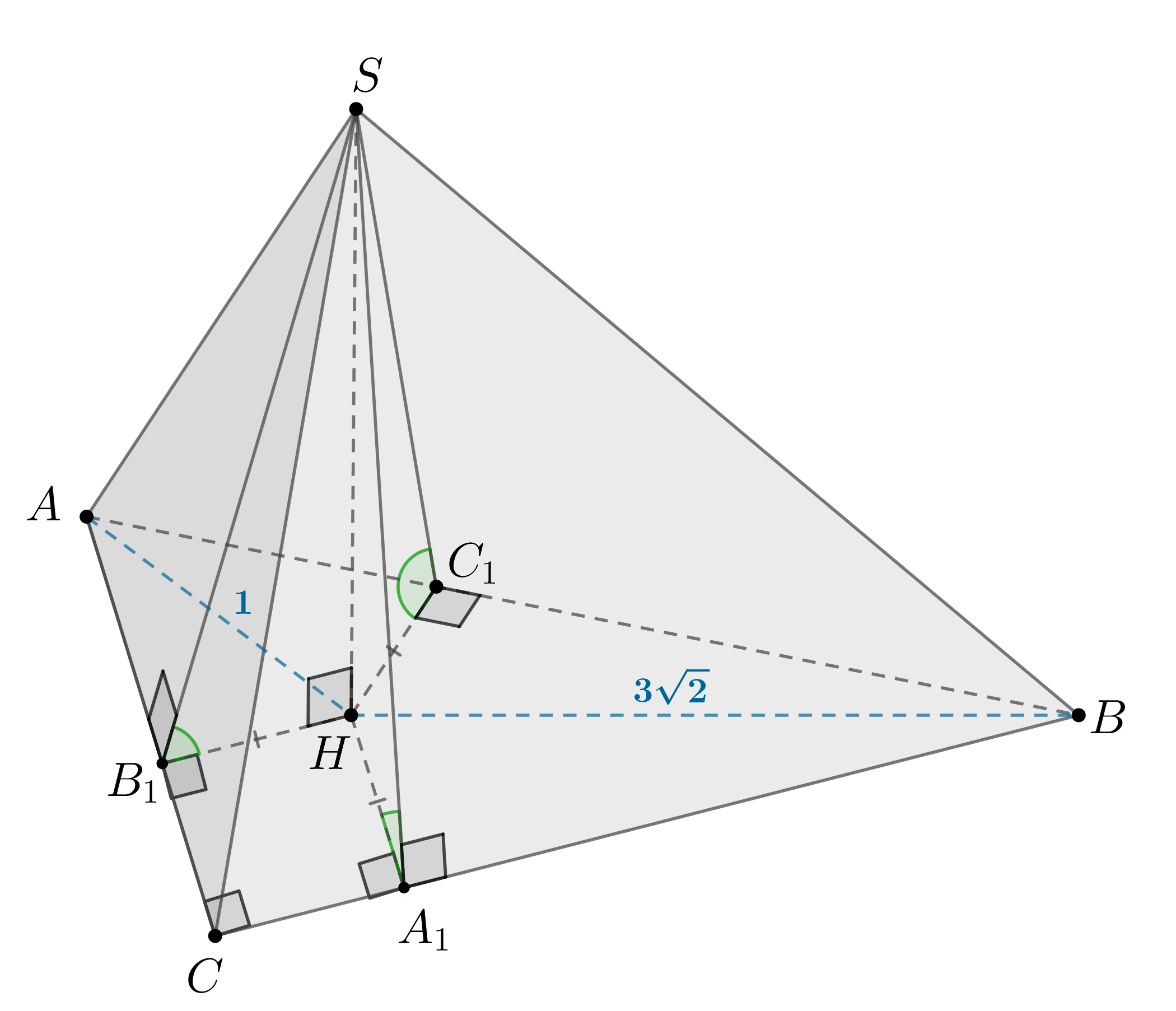
,
— отрезки биссектрис
и
.
Так как в прямоугольном треугольнике синус одного острого угла равен
косинусу другого острого угла, то получаем равенство
Проверим, выполняется ли теорема Пифагора для при найденных
значениях
Заметим, что
,
как отрезки
касательных, проведенных к вписанной окружности из точек
соответственно.
Если , то
,
,
— верно.
Если , то
,
,
— неверно.
Следовательно, . Так как
то
. Так как из
выше приведенного равенства треугольников , то площадь
боковой поверхности пирамиды равна
Ответ:
Найдите двугранный угол при ребре основания правильной треугольной пирамиды,
если угол между ее боковыми ребрами равен
Показать ответ и решение
Ответ:
Докажите теорему косинусов для трехгранного угла:
Косинус плоского угла трехгранного угла равен произведению косинусов
двух других плоских углов и
трехгранного угла, сложенному с
произведением синусов этих углов на косинус двугранного угла при
противолежащем ему ребре:
Показать ответ и решение
а) Высота пирамиды проходит через центр окружности, описанной около основания, значит, боковые рёбра пирамиды равны.
Обозначим Тогда по теореме Пифагора для треугольников
и
Из прямоугольных треугольников и
Следовательно, то есть
— середина
![]()
б) В равнобедренном треугольнике через точку
лежащую на боковой стороне
, проведём прямую,
параллельную высоте Пусть
— точка её пересечения со стороной
По теореме о пропорциональных отрезках
— середина Значит, если
то имеем:
Из прямоугольного треугольника
Из прямоугольного треугольника
![]()
Так как и
то
— линейный угол двугранного угла, образованного гранями
и
По теореме косинусов для
Следовательно, угол между гранями и
равен
Ответ:
б)
Критерии оценки
|
Содержание критерия |
Балл |
|
Имеется верное доказательство |
3 |
|
Обоснованно получен верный ответ в |
2 |
|
ИЛИ |
|
|
имеется верное |
|
|
Имеется верное доказательство |
1 |
|
ИЛИ |
|
|
при обоснованном решении пункта |
|
|
ИЛИ |
|
|
обоснованно получен верный ответ в |
|
|
Решение не соответствует ни одному |
0 |
|
Максимальный балл |
3 |
