Угол между плоскостями.
Определение.
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Определение.
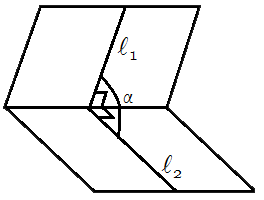
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α = | |A1·A2 + B1·B2 + C1·C2| |
| √A12 + B12 + C12√A22 + B22 + C22 |
Примеры задач на вычисление угла между плоскостями
Пример 1.
Найти угол между плоскостями 2x + 4y – 4z – 6 = 0 и 4x + 3y + 9 = 0.
Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:
cos α =
|2·4 + 4·3 + (-4)·0|√22 + 42 + (-4)2√42 + 32 + 02
=
|8 + 12|√36√25
=
2030
=
23
Ответ: косинус угла между плоскостями равен cos α = 23.
Как найти угол между двумя плоскостями?
Пусть заданы уравнениями две плоскости $$A_1 x + B_1 y + C_1 z + D_1 = 0$$ $$A_2 x + B_2 y + C_2 z + D_2 = 0$$
Запишем нормальные векторы этих плоскостей, каждая координата которых равна соответствующим коэффициентам в уравнениях плоскостей $$overline{n}_1 = (A_1,B_1,C_1)$$$$overline{n}_2 = (A_2,B_2,C_2)$$
Угол между плоскостями – это угол между двумя нормальными векторами этих плоскостей, вычисляемый по формуле: $$cos varphi = frac{(overline{n}_1,overline{n}_2)}{|overline{n}_2| cdot |overline{n}_2|}$$
В числителе формулы стоит скалярное произведение векторов, вычисляемое путем суммирования произведений соответствующих координат
$$(overline{n}_1,overline{n}_2) = A_1 cdot A_2 + B_1 cdot B_2 + C_1 cdot C_2$$
В знаменателе расположено произведение длин векторов, вычисляемых извлечением квадратного корня из суммы квадратов соответствующих координат векторов
$$|overline{n}_1| = sqrt{A_1 ^2 + B_1 ^2 + C_1 ^2}$$
$$|overline{n}_2| = sqrt{A_2 ^2 + B_2 ^2 + C_2 ^2}$$
- Вычисляем скалярное произведение нормальных векторов $(overline{n}_1,overline{n}_2)$
- Находим произведение модулей нормальных векторов $ |overline{n}_1| cdot |overline{n}_2| $
- Подставляем найденные значения в формулу косинуса угла между плоскостями $ cos varphi $
Примеры решений
| Пример 1 |
| Найти угол между плоскостями $3x-y+3=0$ и $x-2y+5z-10=0$ |
| Решение |
|
Записываем нормальные векторы каждой из плоскостей. В качестве координат векторов подставляем коэффициенты из уравнений плоскостей $$ overline{n}_1 = (3,-1,0) $$ $$ overline{n}_2 = (1,-2,5) $$ Вычисляем скалярное произведение, полученных векторов $overline{n}_1$ и $ overline{n}_2$. Выполняем сложение произведений соответствующих координат $$(overline{n}_1,overline{n}_2) = 3cdot 1 + (-1)cdot (-2) + 0cdot 5 = 5$$ Находим модули каждого из векторов. Извлекаем квадратный корень из суммы квадратов соответствующих координат $$|overline{n}_1| = sqrt{3^2 + (-1)^2 + 0^2} = sqrt{10}$$ $$|overline{n}_2| = sqrt{1^2+(-2)^2+5^2} = sqrt{30}$$ Подставляем полученные значения в формулу нахождения угла между плоскостями $$cos varphi = frac{5}{sqrt{10} cdot sqrt{30}} = frac{1}{sqrt{12}}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$varphi = arccosfrac{1}{sqrt{12}}$$ |
Рассмотрим
две плоскости α1 и α2, заданные соответственно
уравнениями:
Под
углом между двумя плоскостями будем
понимать один из двугранных углов,
образованных этими плоскостями. Очевидно,
что угол между нормальными


Под
углом между двумя плоскостями будем
понимать один из двугранных углов,
образованных этими плоскостями. Очевидно,
что угол между нормальными векторами
п1 и п2 плоскостей α1 и α2 равен одному из
указанных смежных двугранных углов
двугранных
углов
или
Поэтому
Т.к.
и
, то
17.Условия параллельности и перпендикулярности плоскостей.
Условие
перпендикулярности плоскостей.
Ясно,
что две плоскости перпендикулярны тогда
и только тогда, когда их нормальные
векторы перпендикулярны, а следовательно
,
или
.
Таким
образом, .
Условие
параллельности двух плоскостей.
Две
плоскости α1 и α2 параллельны тогда и
только тогда, когда их нормальные векторы
п1 и п2 параллельны, а значит .
Итак,
две плоскости параллельны друг другу
тогда и только тогда, когда коэффициенты
при соответствующих координатах
пропорциональны:
или
18.Прямая в пространстве: общие, параметрические и канонические уравнения, их эквивалентность; уравнения прямой, проходящей через две данные точки.
ОБЩИЕ
УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ
ДВУХ ПЛОСКОСТЕЙ
Через
каждую прямую в пространстве проходит
бесчисленное множество плоскостей.
Любые две из них, пересекаясь, определяют
ее в пространстве. Следовательно,
уравнения любых двух таких плоскостей,
рассматриваемые совместно представляют
собой уравнения этой прямой.
Вообще
любые две не параллельные плоскости,
заданные общими уравнениями

определяют
прямую их пересечения. Эти уравнения
называются общими уравнениями прямой.
–Пусть
заданы две точки М1(х1, у1, z1)
и М2(х2, у2, z2),
через которые должна проходить прямая
линия. Примем за направляющий вектор
прямой вектор
.
Поэтому
уравнение (13.4) примет вид

Положение
прямой в пространстве вполне определяется
заданием какой-либо её фиксированной
точки М1 и S
вектора , параллельного этой прямой.
Вектор
S,
параллельный прямой, называется
направляющим вектором этой прямой.
Итак,
пусть прямая l проходит через точку
М1(x1, y1, z1), лежащую на прямой параллельно
вектору
.
Рассмотрим
произвольную точку М(x,y,z) на прямой. Из
рисунка видно, что
Векторы
и коллинеарны, поэтому найдётся такое
число t, что
,
где множитель t может принимать любое
числовое значение в зависимости от
положения точки M на прямой. Множитель
t называется параметром. Обозначив
радиус-векторы точек М1 и М соответственно
через
и
,
получаем . Это уравнение называется
векторным уравнением прямой. Оно
показывает, что каждому значению
параметра t соответствует радиус-вектор
некоторой точки М, лежащей на прямой.
Запишем
это уравнение в координатной форме.
Заметим, что ,
и
и
отсюда

Полученные
уравнения называются параметрическими
уравнениями прямой.
При
изменении параметра t изменяются
координаты x, y и z и точка М перемещается
по прямой.
КАНОНИЧЕСКИЕ
УРАВНЕНИЯ ПРЯМОЙ

Пусть
М1(x1, y1, z1) – точка, лежащая на прямой l, и
– её направляющий вектор. Вновь возьмём
на прямой произвольную точку М(x,y,z) и
рассмотрим вектор
.
Ясно,
что векторы
и S
коллинеарные, поэтому их соответствующие
координаты должны быть пропорциональны,
следовательно,
–
канонические
уравнения прямой.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Здравствуйте, дорогие подписчики и гости канала. Сегодня разбираем 13 задачу с сайта РЕШУ ЕГЭ
Вот условие задачи
Первое легко доказывается с помощью теоремы о трех перпендикулярах:
Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной
Теперь зная, что А1Н перпендикурно BD легко найти угол между плоскостями – это угол между перпендикулярами, проведенными к линии пересечения плоскостей, то есть угол между А1Н и АН
Рассмотрим прямоугольный треугольник АА1Н
Найдем тангенс угла А1АН:
Спасибо за внимание
Буду рада вашим лайкам, комментариям и вашей подписке
Также приглашаю на канал в
Телеграм и в группу Вконтакте
До новых встреч на канале Простаяматематика.рф
Угол между плоскостями
Содержание:
- Углы между плоскостями — обозначение
-
Расположение плоскостей и формула вычисления угла между ними
- Параллельность
- Перпендикулярность
- Угол между плоскостями
- Примеры решения задач
Углы между плоскостями — обозначение
Определение
Углом между плоскостями именуется такой угол, который образовался между перпендикулярными прямыми, опущенными в пределах этих плоскостей к линии их пересечения.
Рассмотрим данное понятие наглядно с помощью картинки:
Допустим, α и β — пересекающиеся плоскости. Проведем к линии с перпендикуляр a, который принадлежит α. Далее проведем прямую b, лежащую в β и образующую с прямой c угол в 90°. Угол между α и β равен углу, который образовался между а и b, обозначенному на картинке как φ. В записи это выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
∠(α, β)=∠(а, b)=φ
На схеме видно, что при пересечении α и β возникают четыре угла, но углом между плоскостями считается острый угол. В случае, когда плоскости при пересечении создают прямые углы, они считаются перпендикулярными друг другу.
Расположение плоскостей и формула вычисления угла между ними
Существует несколько вариаций взаимного расположения двух плоскостей.
Параллельность
Теорема
Две плоскости считаются параллельными в том случае, если у них отсутствуют общие точки.
Возьмем за условие, что плоскости α, расположенной в некоторой прямоугольной системе координат, соответствует общее уравнение: А1х+В1у+С1z+D1=0. А плоскость β определяется общим уравнением вида: А2х+В2у+С2z+D2=0.
Согласно теореме о параллельности плоскостей, чтобы α и β являлись параллельными, достаточно отсутствия решений системы линейных уравнений вида:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
То есть приведенная выше система должна быть несовместной.
Доказательство
Допустим, указанные плоскости, соответствующие уравнениям А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 параллельны друг другу, следовательно, у них отсутствуют общие точки. Это значит, что нет ни одной точки в прямоугольной системе координат, находящейся в трехмерном пространстве, чьи координаты отвечали бы условиям обоих уравнений одновременно или:
(left{begin{array}{l}A_1x+B_1y+C_1z+D_1=0\A_2x+B_2y+C_2z+D_2=0end{array}right.)
не имеет решения.
В случае, если данная система уравнений не имеет решений, то в прямоугольной системе координат трехмерного пространства отсутствуют точки с координатами, одновременно отвечающими условиям обоих уравнений, входящих в рассматриваемую систему. Отсюда можно сделать вывод, что плоскости α и β с соответствующими им уравнениями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 не обладают ни одной общей точкой, а значит, являются параллельными. Теорема доказана.
Перпендикулярность
Две плоскости перпендикулярны друг другу, в ситуации, когда они при взаимном пересечении образуют прямой угол, то есть угол в 90°.
Теорема
Если одна из двух плоскостей проходит через прямую, которая перпендикулярна другой плоскости, то такие плоскости являются перпендикулярными.
Доказательство
Пусть: AB∈α, AB⊥β, AB∩β=A.
Необходимо доказать, что α⊥β.
- α∩β=AC, причем AB⊥AC по условию.
- Проведем прямую AD, принадлежащую плоскости β и перпендикулярную AC.
- ∠BAD=90°, поскольку AB⊥β. Следовательно, заданные плоскости перпендикулярны, что и требовалось доказать.
Следствие
Плоскость, перпендикулярная к прямой, по которой пересекаются две заданные плоскости, перпендикулярна к каждой из этих плоскостей.
Теорема
Явность перпендикулярных пересекающихся плоскостей достигается при необходимом и достаточном условии, что нормальные векторы данных плоскостей при пересечении образовали прямой угол.
Доказательство
Допустим, в трехмерном пространстве существует некоторая прямоугольная система координат. При наличии нормальных векторов заданных плоскостей α и β с координатами:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2),)
то необходимо и достаточно, чтобы эти векторы приняли вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Отсюда следует, что:
(overrightarrow{n_1}=(A_1,B_1,C_1),)
(overrightarrow{n_2}=(A_2,B_2,C_2))
— нормальные векторы плоскостей α и β. Чтобы заданные плоскости были перпендикулярными, достаточно, чтобы скалярное произведение данных векторов ровнялось нулю, то есть принимало вид:
(left(overrightarrow{n_1},overrightarrow{;n_2}right)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Равенство соблюдено.
Угол между плоскостями
Для вычисления угла между двумя пересекающимися плоскостями используют метод координат. Суть данного способа заключается в нахождении косинуса угла, образованного при пересечении плоскостей.
Предположим, что плоскости P1 и P2 заданы следующими уравнениями:
(P_1:;A_1x+B_1y+C_1z+D_1=0,;{overline N}_1=left(A_1,B_1,C_1right);)
(P_2:;A_2x+B_2y+C_2z+D_2=0,;{overline N}_2=left(A_2,B_2,C_2right))
Найдем косинус угла между P1 и P2 по формуле:
(cosleft(overbrace{P_1,P_2}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}frac{A_1times A_2+B_1times B_2+C_1times C_2}{sqrt{A_1^2+B_1^2+C_1^2}timessqrt{A_2^2+B_2^2+C_2^2}})
Запишем в ответе модуль косинуса угла, поскольку за величину угла между плоскостями принимают острый угол.
Примеры решения задач
Задача №1
Плоскости заданы уравнениями:
(alpha:;x-y+1=0)
(beta:y-z+1=0)
Определить пересекаются ли α и β. В случае пересечения заданных плоскостей найти угол между ними.
Решение:
Найдем угол между заданными плоскостями:
(alpha:;x-y+1=0,Rightarrowoverline{N_1}=(1,-1,0);)
(beta:;y-z+1=0,Rightarrowoverline{N_2}=(0,1,-1))
Далее вычислим косинус угла между α и β:
(cosleft(overbrace{alpha,beta}right)=frac{overline{N_1}timesoverline{N_2}}{left|overline{N_1}right|timesleft|overline{N_2}right|}=frac{1times0+left(-1right)times1+0timesleft(-1right)}{sqrt{1^2+left(-1right)^2+0^2}timessqrt{0^2+1^2+left(-1right)^2}}=frac{-1}{sqrt4}=-frac12)
В ответе запишем модуль найденной величины.
Ответ: плоскости α и β пересекаются, а косинус угла между ними равен ½.
Задача №2
Плоскость α проходит через точку A(1,1,−1) и перпендикулярна к плоскостям, заданным уравнениями:
(beta:;2x-y+5z+3=0;)
(varphi:;x+3y-z-7=0)
Составьте уравнение плоскости α.
Решение:
Необходимым и достаточным условием перпендикулярности α к плоскостям β и φ является параллельность α к нормалям β и φ — N1 и N2, иными словами, α должна быть перпендикулярна к произведению векторов [N1,N2].
(x = {-b pm sqrt{b^2-4ac} over 2a}beta:;2x-y+5z+3=0,Rightarrow;overline{N_1}=left(2,-1,5right))
(varphi:;x+3y-z-73=0,Rightarrow;overline{N_2}=left(1,3,-1right))
(left[N_1,N_2right]=begin{vmatrix}i&j&k\2&-1&5\1&3&-1end{vmatrix}=ileft(1-15right)-jleft(-2-5right)+kleft(6+1right)=-14i+7j+7k)
Следующим шагом выпишем уравнение плоскости α, проходящей через точку A(1,1,−1) и перпендикулярную вектору [N1,N2]=(−14,7,7):
(-14left(x-1right)+7left(y-1right)+7left(z+1right)=left.0right|:7)
(-2left(x-1right)+y-1+z+1=0)
(−2x+y+z+2=0)
Ответ: (−2x+y+z+2=0.)