Статья начинается с определение угла между прямой и плоскостью. В данной статье будет показано нахождение угла между прямой и плоскостью методом координат. Подробно будут рассмотрены решение примеров и задач.
Угол между прямой и плоскостью – определение
Предварительно необходимо повторить понятие о прямой линии в пространстве и понятие плоскости. Для определения угла между прямой и плоскостью необходимый несколько вспомогательных определений. Рассмотрим эти определения подробно.
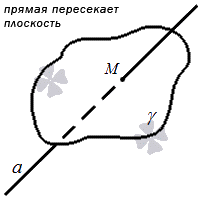
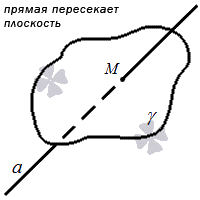
Прямая и плоскость пересекаются в том случае, когда они имеют одну общую точку, то есть она является точкой пересечения прямой и плоскости.
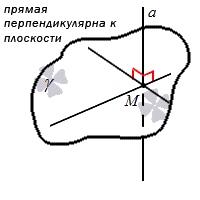
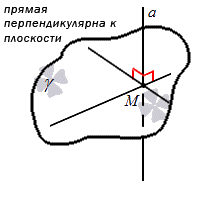
Прямая, пересекающая плоскость, может являться перпендикулярной относительно плоскости.
Прямая является перпендикулярной к плоскости, когда она перпендикулярна любой прямой, находящейся в этой плоскости.
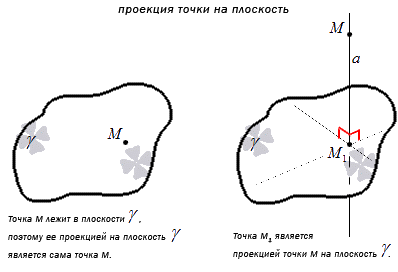
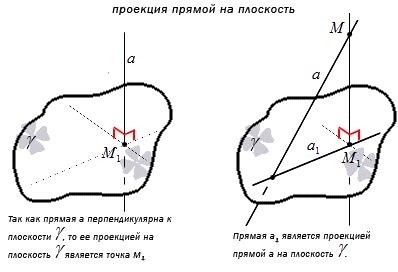
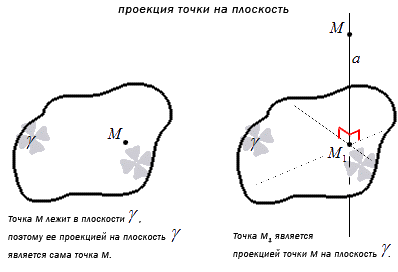
Проекция точки M на плоскость γ является сама точка, если она лежит в заданной плоскости, либо является точкой пересечения плоскости с прямой, перпендикулярной плоскости γ, проходящей через точку M, при условии, что она не принадлежит плоскости γ.
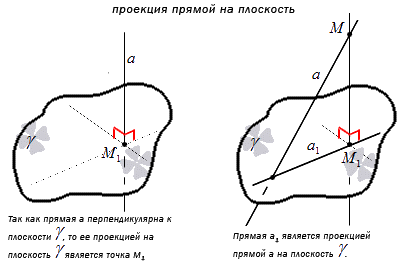
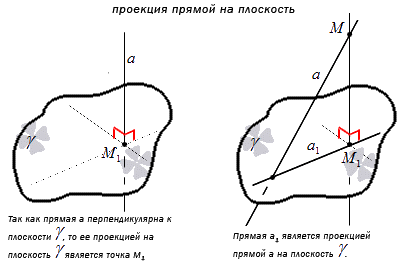
Проекция прямой а на плоскость γ – это множество проекций всех точек заданной прямой на плоскость.
Отсюда получаем, что перпендикулярная к плоскости γ проекция прямой имеет точку пересечения. Получаем, что проекция прямой a – это прямая, принадлежащая плоскости γ и проходящая через точку пересечения прямой a и плоскости. Рассмотрим на рисунке, приведенном ниже.
На данный момент имеем все необходимые сведения и данные для формулировки определения угла между прямой и плоскостью
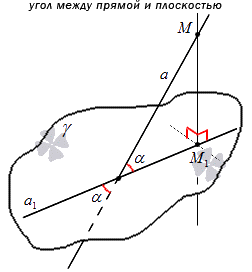
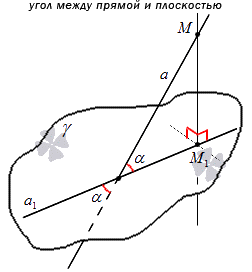
Углом между прямой и плоскостью называют угол между этой прямой и ее проекцией на эту плоскость, причем прямая не перпендикулярна к ней.
Определение угла, приведенное выше, помогает прийти к выводу о том, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми, то есть заданной прямой вместе с ее проекцией на плоскость. Значит, угол между ними всегда будет острым. Рассмотрим на картинке, приведенной ниже.
Угол, расположенный между прямой и плоскостью, считается прямым, то есть равным 90 градусов, а угол, расположенный между параллельными прямыми, не определяется. Бывают случаи, когда его значение берется равным нулю.
Нахождение угла между прямой и плоскостью
Задачи, где необходимо найти угол между прямой и плоскостью, имеет множество вариация решения. Ход самого решения зависит от имеющихся данных по условию. Частыми спутниками решения являются признаки подобия или равенства фигур, косинусы, синусы, тангенсы углов. Нахождение угла возможно при помощи метода координат. Рассмотрим его более детально.
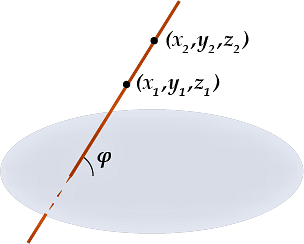
Если в трехмерном пространстве вводится прямоугольная система координат Охуz, тогда в ней задается прямая a, пересекающая плоскость γ в точке M, причем она не перпендикулярна плоскости. Необходимо найти угол α, находящийся между заданной прямой и плоскостью.
Для начала необходимо применить определение угла между прямой и плоскостью методом координат. Тогда получим следующее.
В системе координат Охуz задается прямая a, которой соответствуют уравнения прямой в пространстве и направляющий вектор прямой пространства, для плоскости γ соответствует уравнение плоскости и нормальный вектор плоскости. Тогда a→=(ax, ay, az) является направляющим вектором заданной прямой a, а n→(nx, ny, nz) – нормальным вектором для плоскости γ. Если представить, что у нас имеются координаты направляющего вектора прямой a и нормального вектора плоскости γ, тогда известны их уравнения, то есть заданы по условию, тогда есть возможность определения векторов a→ и n→, исходя из уравнения.
Для вычисления угла необходимо преобразовать формулу, позволяющую получить значение этого угла при помощи имеющихся координат направляющего вектора прямой и нормального вектора.
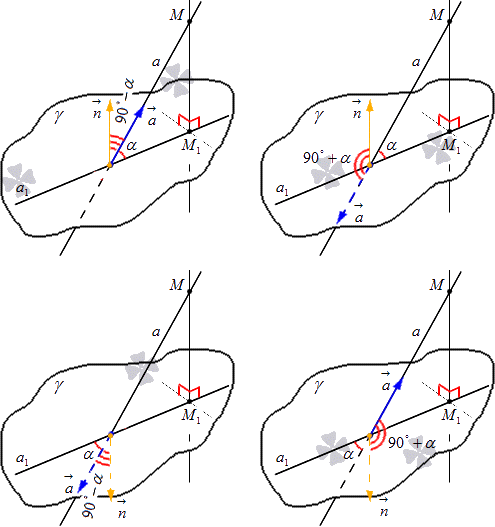
Необходимо отложить векторы a→ и n→, начиная от точки пересечения прямой a с плоскостью γ. Существуют 4 варианта расположения этих векторов относительно заданных прямых и плоскости. Рассмотри рисунок, приведенный ниже, на котором имеются все 4 вариации.
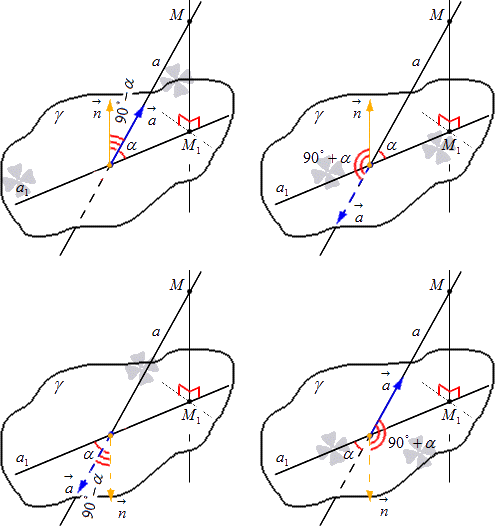
Отсюда получаем, что угол между векторами a→ и n→ имеет обозначение a→, n→^ и является острым, тогда искомый угол α , располагающийся между прямой и плоскостью, дополняется, то есть получаем выражение вида a→, n→^=90°-α. Когда по условию a→, n→^>90°, тогда имеем a→, n→^=90°+α.
Отсюда имеем, что косинусы равных углов являются равными, тогда последние равенства записываются в виде системы
cosa→, n→^=cos 90°-α, a→, n→^<90°cosa→, n→^=cos 90°+α, a→, n→^>90°
Необходимо использовать формулы приведения для упрощения выражений. Тогда получим равенства вида cosa→, n→^=sin α, a→, n→^<90°cosa→, n→^=-sin α, a→, n→^>90°.
Проведя преобразования, система приобретает вид sin α=cosa→, n→^, a→, n→^<90°sin α=-cosa→, n→^, a→, n→^>90°⇔sin α=cosa→, n→^, a→, n→^>0sin α=-cosa→, n→^, a→, n→^<0⇔⇔sin α=cosa→, n→^
Отсюда получим, что синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором заданной плоскости.
Раздел нахождения угла, образованного двумя векторами, выявили, что этот угол принимает значение скалярного произведения векторов и произведения этих длин. Процесс вычисления синуса угла, полученного пересечением прямой и плоскости, выполняется по формуле
sin α=cosa→, n→^=a→, n→^a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2
Значит, формулой для вычисления угла между прямой и плоскостью с координатами направляющего вектора прямой и нормального вектора плоскости после преобразования получается вида
α=arcsina→, n→^a→·n→=arcsinax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2
Нахождение косинуса при известном синусе позволительно, применив основное тригонометрическое тождество. Пересечение прямой и плоскости образует острый угол. Это говорит о том, что его значение будет являться положительным числом, а его вычисление производится из формулы cos α=1-sin α.
Выполним решение нескольких подобных примеров для закрепления материала.
Найти угол, синус, косинус угла, образованного прямой x3=y+1-2=z-116 и плоскостью 2x+z-1=0.
Решение
Для получения координат направляющего вектора необходимо рассмотреть канонические уравнения прямой в пространстве. Тогда получим, что a→=(3, -2, 6) является направляющим вектором прямой x3=y+1-2=z-116.
Для нахождения координат нормального вектора необходимо рассмотреть общее уравнение плоскости, так как их наличие определяется коэффициентами, имеющимися перед переменными уравнения. Тогда получим, что для плоскости 2x+z-1=0 нормальный вектор имеет вид n→=(2, 0, 1).
Необходимо перейти к вычислению синуса угла между прямой и плоскостью. Для этого необходимо произвести подстановку координат векторов a→ и b→ в заданную формулу. Получаем выражение вида
sin α=cosa→, n→^=a→, n→^a→·n→=ax·nx+ay·ny+az·nzax2+ay2+az2·nx2+ny2+nz2==3·2+(-2)·0+6·132+(-2)2+62·22+02+12=1275
Отсюда найдем значение косинуса и значение самого угла. Получим:
cos α=1-sin α=1-12752=10175
Ответ: sin α=1275, cos α=10175, α=arccos10175=arcsin1275.
Имеется пирамида, построенная при помощи значений векторов AB→=1, 0, 2, AC→=(-1, 3, 0), AD→=4, 1, 1. Найти угол между прямой AD и плоскостью АВС.
Решение
Для вычисления искомого угла, необходимо иметь значения координат направляющего вектора прямой и нормального вектора плоскости. для прямой AD направляющий вектор имеет координаты AD→=4, 1, 1.
Нормальный вектор n→, принадлежащий плоскости АВС, является перпендикулярным вектору AB→ и AC→. Это подразумевает то, что нормальным вектором плоскости АВС можно считать векторное произведение векторов AB→ и AC→. Вычислим это по формуле и получим:
n→=AB→×AC→=i→j→k→102-130=-6·i→-2·j→+3·k→⇔n→=(-6, -2, 3)
Необходимо произвести подстановку координат векторов для вычисления искомого угла, образованного пересечением прямой и плоскости. получим выражение вида:
α=arcsinAD→, n→^AD→·n→=arcsin4·-6+1·-2+1·342+12+12·-62+-22+32=arcsin23212
Ответ: arcsin23212.
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
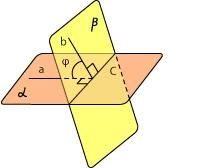
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
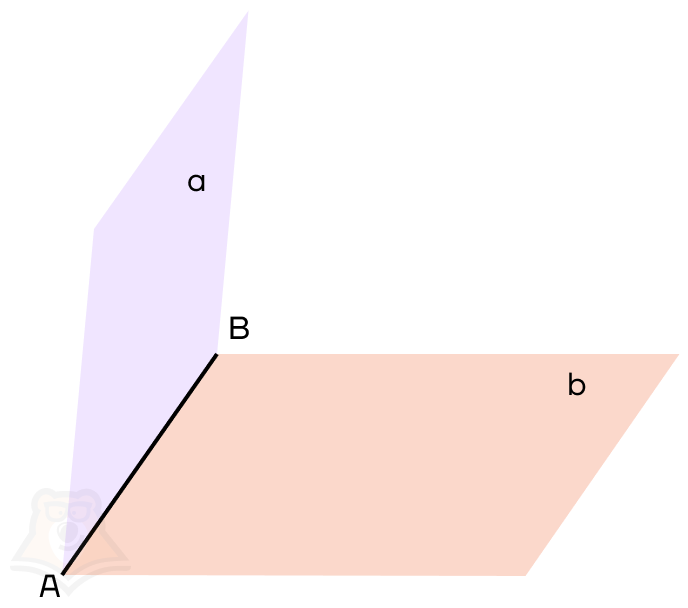
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
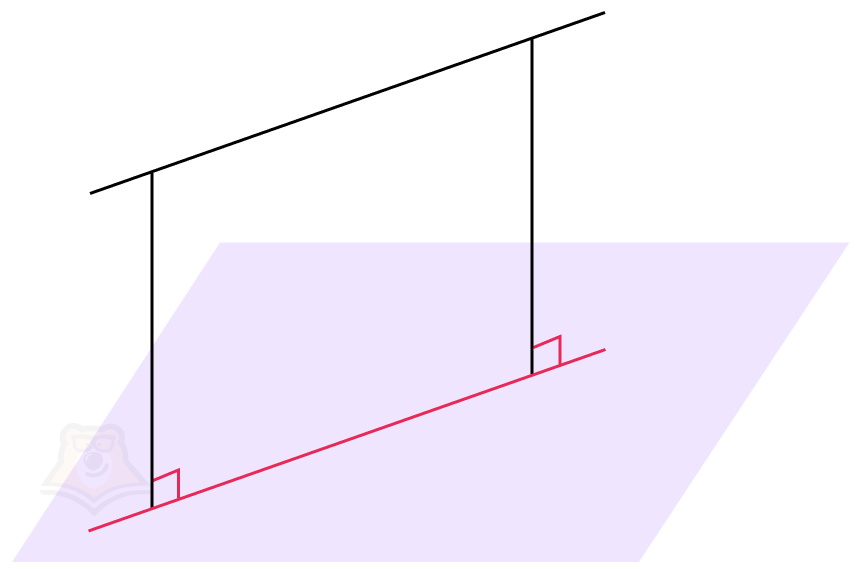
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
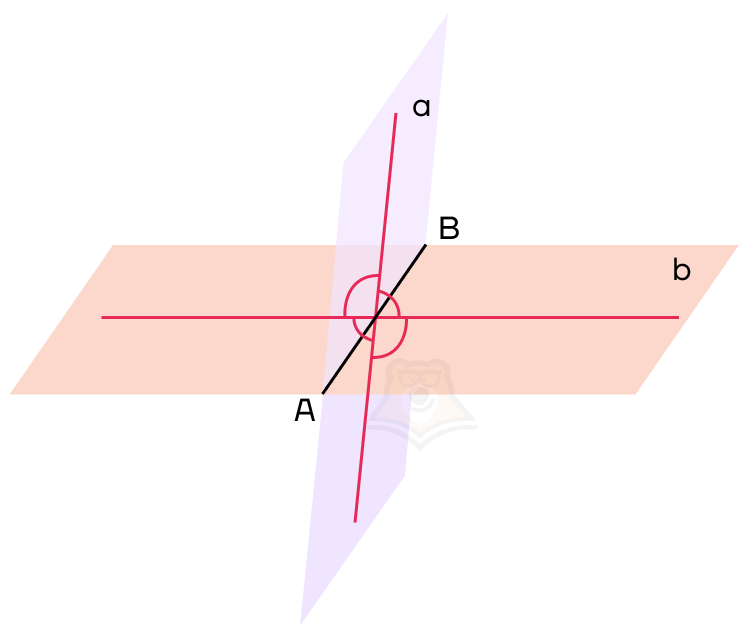
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
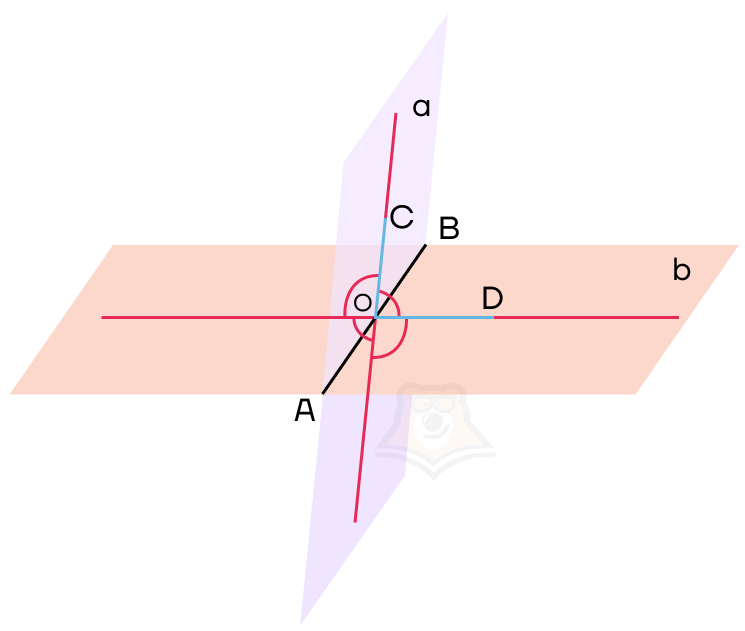
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
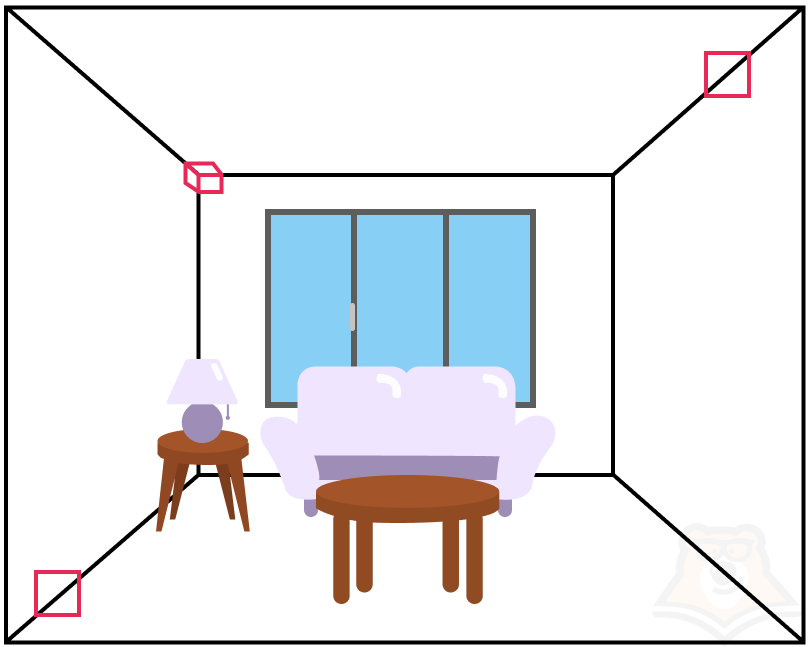
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
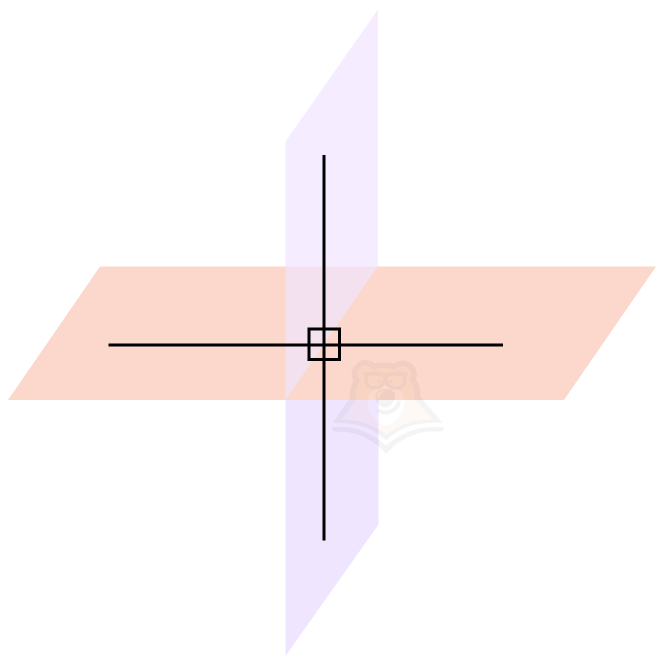
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
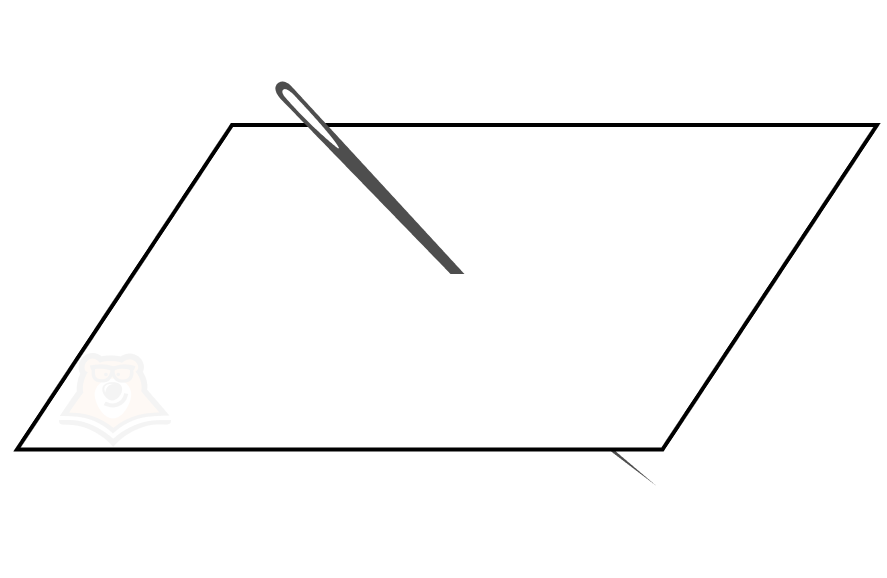
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
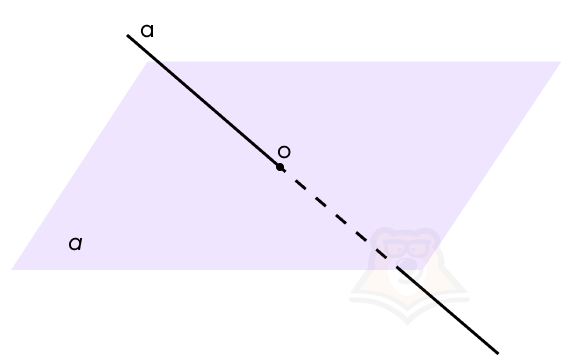
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
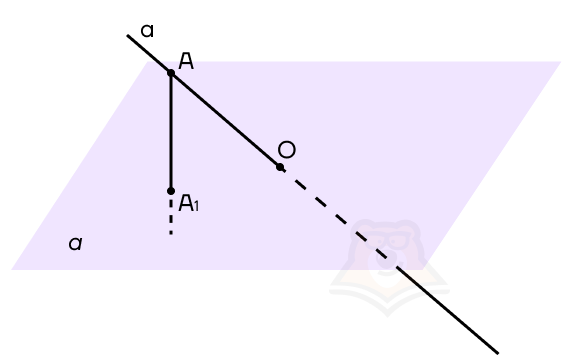
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
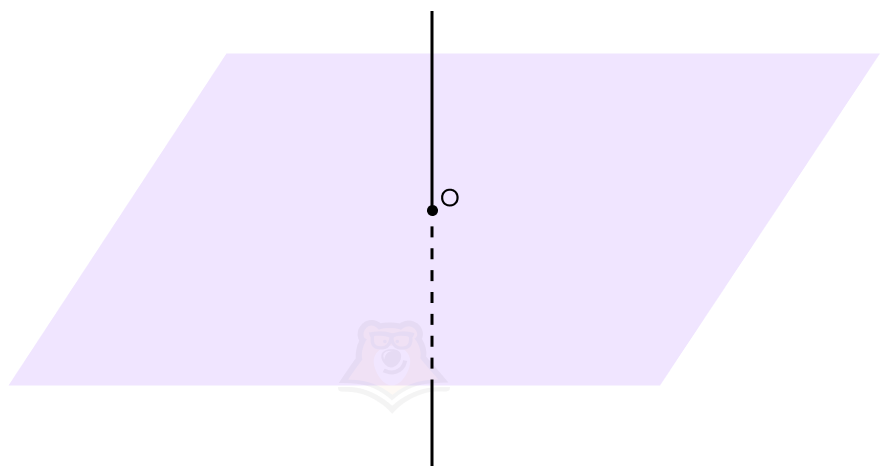
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
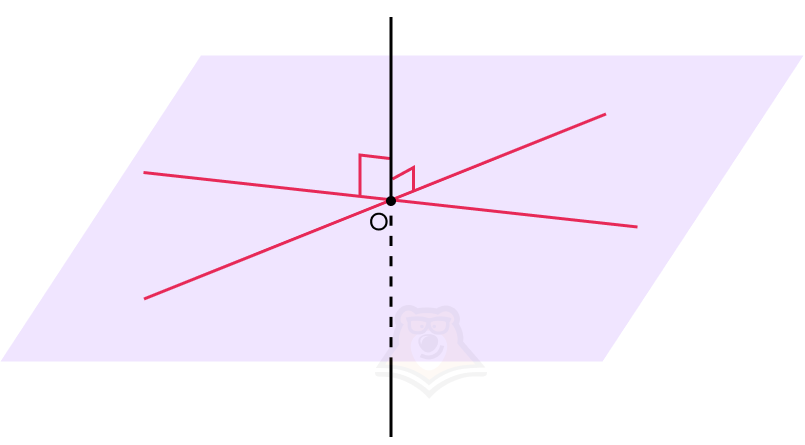
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
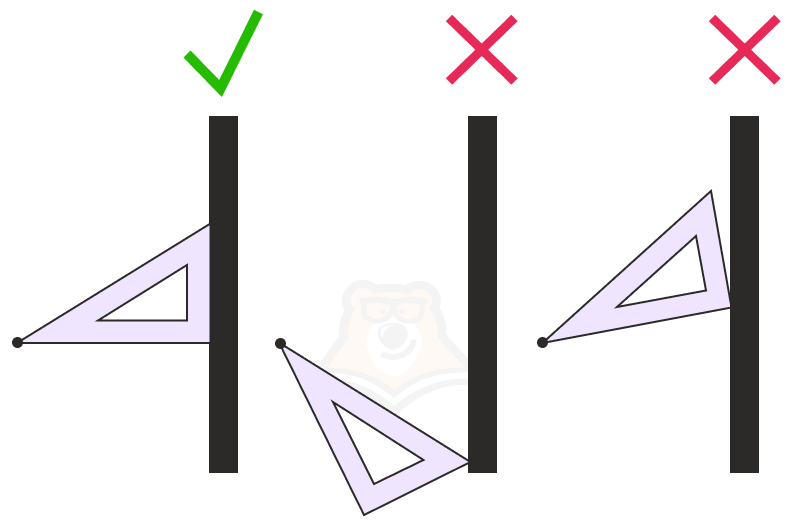
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

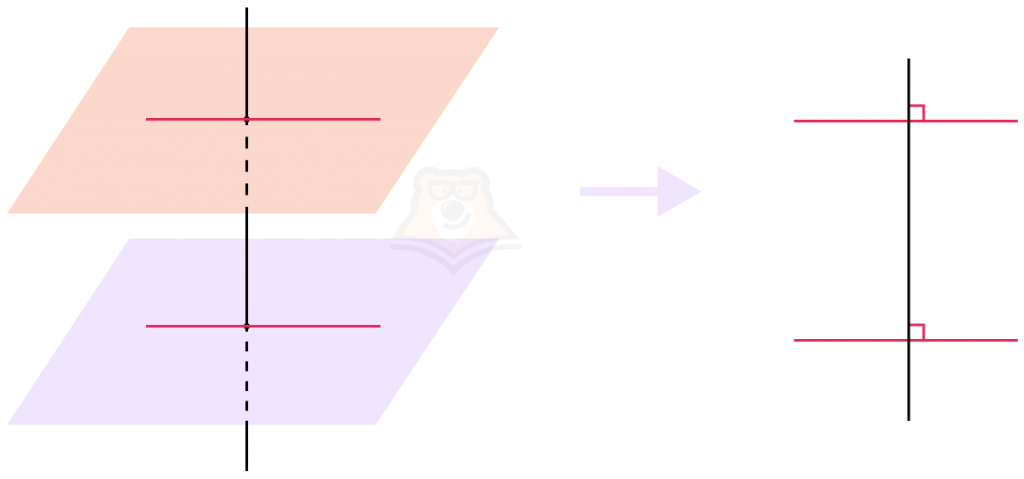
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
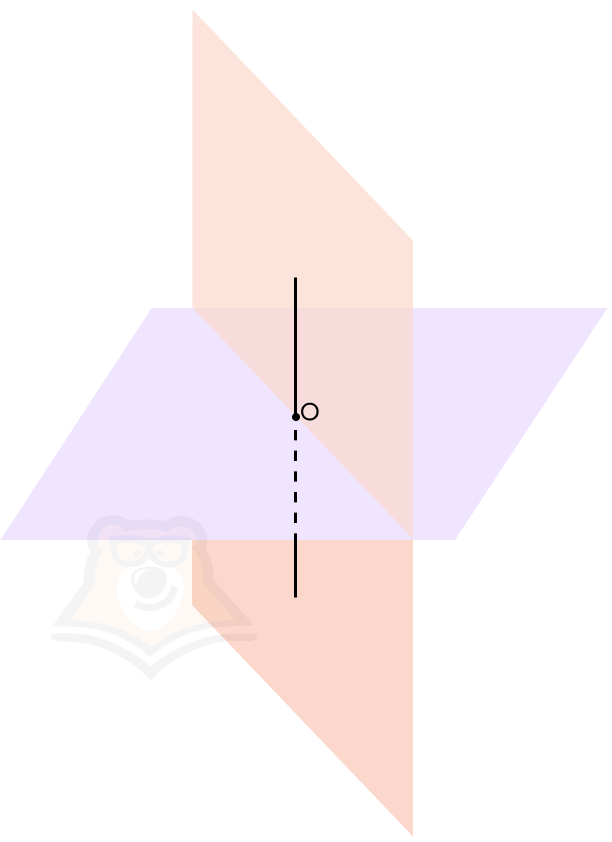
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
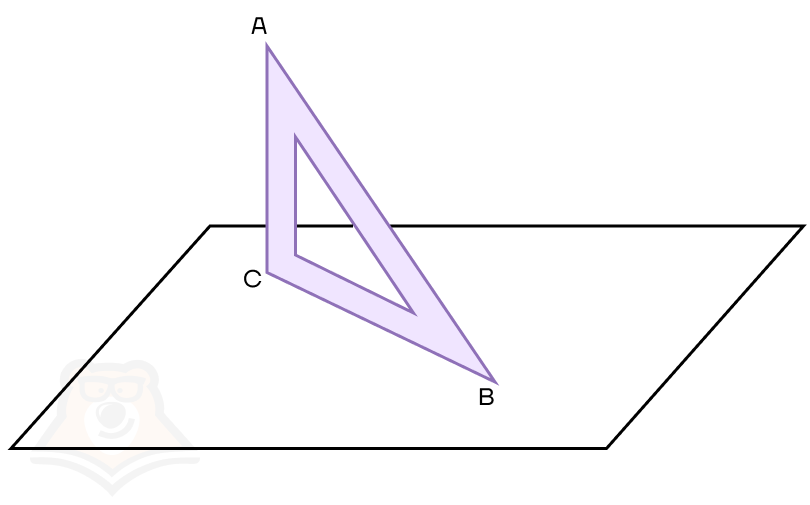
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
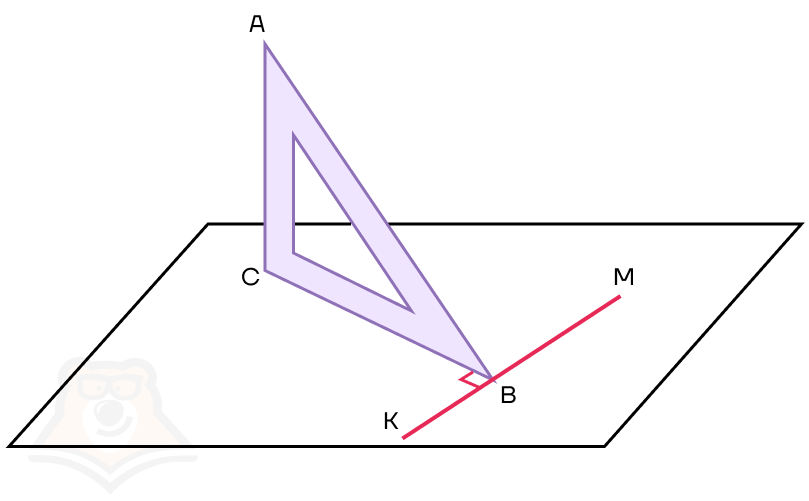
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
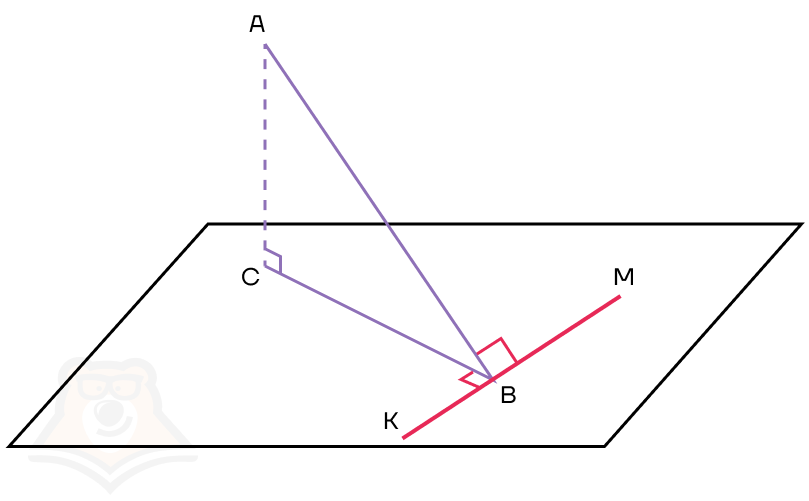
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Бонусы: вебинары из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ 14. Стереометрия. Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой — это первое видео раздела «Стереометрия», входящее в полный курс подготовки к ЕГЭ (о нем ниже).
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ №14. Стереометрия. Разбор варианта профильного ЕГЭ
Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
Об этом в нашем вебинаре в задаче о шестиугольной призме.
ЕГЭ 14 Стереометрия. Разбора задачи статграда, февраль 2021
Что проще: призма или пирамида? Хоть в призме и больше рёбер и граней, но с пирамидами справляться сложнее, причём прямо начиная с рисунка: все линии налезают друг на друга, ничего нигде не параллельно, в общем, лучше бы призму дали.
Но как только научились рисовать пирамиду, сразу всё стало проще: кругом одни треугольники, а как известно, фигур проще треугольника в геометрии найти не так-то просто 🙂
А если где прямые углы найдём, то вообще сказка.
Из этого видео вы узнаете, как правильно рисовать пирамиду и научитесь решать задачу №14 из февральского СтатГрада
Основное определение: «Угол, возникающий между перпендикулярными отрезками, опущенными в пределах этих плоскостей к линии пересечения и является углом между плоскостями».
Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция.
Виды углов между плоскостью
Плоскость и прямая имеют одну точку пересечения (общую).
В данном примере угол между прямой и плоскостью нам не известен. Прямая также может проходить через плоскость перпендикулярно (90 градусов)
Прямая перпендикулярна плоскости, а также всем остальным прямым, расположенным на данной плоскости.
Точка перпендикулярного пересечения прямой М1 и плоскости γ под является одновременно и проекцией точки М, при условии, что она не принадлежит плоскости γ.
Проекция прямой на плоскость обозначает множество проекция данной прямой на плоскость.
Это означает, что прямая, перпендикулярная к плоскости имеет с ней общую точку пересечения, из чего следует то, что a – принадлежит плоскости и проходящей через точку пересечения прямой плоскости.
Углом между прямой и плоскостью является угол между данной прямой и ее проекцией на заданную плоскость.
Прямая необязательно перпендикулярна плоскости. Из этого обозначения следует, что угол между прямой и плоскостью всегда является острым (90>x).
Угол между прямой и плоскостью всегда равен 90 градусам, в то время как угол между параллельно расположенными прямыми определять не требуется. В некоторых заданиях, его значение просто приравнивается нулю, это указывают внутри задания.
Нет времени решать самому?
Наши эксперты помогут!
Как найти угол между прямой и плоскостью
Способов решения задач на нахождения угла между плоскостью и заданной прямой, бесчисленное множество. Путь, которым необходимо решить задачу, выбирается исходя из указанных в условиях задачи данных. Зачастую, рельсами решения задач такого типа являются тангенсы, косинусы, синусы углов, а также признаки подобия/равенства фигур. Далее будет рассмотрен метод решения с применением сетки координат.
Геометрический метод. При геометрическом методе нужно найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя представляет проекция, а потом решать планиметрическую задачу по поиску угла (φ) в треугольнике (зачастую прямоугольном).
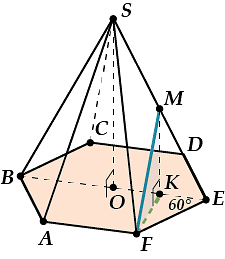
Решение задачи геометрическим методом. Поскольку в правильной пирамиде высота опускается в центр основания O, то OE – это проекция SE, а точка M проецируется в точку K – середину отрезка OE.
И теперь FK – это проекция FM, а искомый угол между прямой FM и плоскостью основания – это ∠MFK.
Ищем этот угол. Пусть стороны основания равны какому – то a, тогда боковые рёбра – 3a. Заметь, что ΔMFK – прямоугольный и в этом треугольнике нам нужно найти острый угол.
Алгебраический метод. При алгебраическом методе вводится система координат, определяются координаты двух точек на прямой и уравнение плоскости, а затем применяется формула вычисления угла между прямой и плоскостью.
[
sin varphi=left|frac{Aleft(x_{2}-x_{1}right)+Bleft(y_{2}-y_{1}right)+Cleft(z_{2}-z_{1}right)}{sqrt{A^{2}+B^{2}+C^{2}} sqrt{left(x_{2}-x_{1}right)^{2}+left(y_{2}-y_{1}right)^{2}+left(z_{2}-z_{1}right)^{2}}}right|
]
Здесь [left(x_{1}, y_{1}, z_{1}right),left(x_{2}, y_{2}, z_{2}right)] — координаты двух точек на прямой, A, B, C- координаты в уравнении плоскости: [ A x+B y+C z+D=0 ].
В 3D используется система координат, состоящая из трех направлений – Охуz.
В ней задается прямая, которая пересекается с заданной плоскостью в точке М. В данном примере требуется найти угол а, который находится между прямой и плоскостью.
Для нахождения угла а, возьмем уравнение прямой и вектор прямой пространства, а плоскости соответствует равенство плоскости и вектор плоскости. Из этого следует: → a = ( a x , a y , a z ).
[vec{a}=left(a_{x}, a_{y}, a_{z}right)] — есть направляющий вектор данной прямой, в то время как → n ( n x , n y , n z ) является нормальным вектором для заданной плоскости. [vec{n}left(n_{x}, n_{y}, n_{z}right)].
При помощи уравнения, в случае если в задании уже есть координаты направляющего вектора прямой и нормального вектора плоскости можно найти векторы а и n.
Имеющуюся у нас формулу моно преобразовать, что позволит получить требуемый угол, применяя координаты направляющего вектора прямой и нормального вектора.
Всего есть 4 возможных варианта расположения векторов а и n относительно данных прямых и плоскости. На рисунке ниже даны все 4 разновидности их расположения.
Угол между указанными векторами обозначается как ( ˆ→ a , → n ) [vec{a}=left(a_{x}, a_{y}, a_{z}right)], являясь острым. Необходимый нам угол а дополняется. Теперь мы имеем выражение [(overbrace{{vec{a}}, vec{n}})=90^{circ}-alpha].
Если по условию задачи [(overbrace{vec{a}, vec{n}})>90^{circ}] ( ˆ → a , → n ) > 90 °,то получается выражение ( ˆ → a , → n ) = 90 ° + α.
[( overbrace{{vec{a}}, vec{n}})=90^{circ}+alpha]
Также необходимо добавить. Что косинусы равных углов равны. Исходя из этого можно составить равенства:
[
cos (widehat{vec{a}, vec{n}})=cos left(90^{circ}-alpharight),(widehat{vec{a}, vec{n}})<90^{circ}
]
[
cos (widehat{vec{a}, vec{n}})=cos left(90^{circ}+alpharight),(widehat{vec{a}, vec{n}})>90^{circ}
]
При помощи формулы приведения можно упростить выражение. Получится:
[
cos (widehat{vec{a}, vec{n}})=sin alpha,(widehat{vec{a}, vec{n}})<90^{circ}
]
[
cos (widehat{vec{a}, vec{n}})=-sin alpha,(widehat{vec{a}, vec{n}})>90^{circ}
]
После некоторых преобразований вырисовывается система:
[
sin alpha=cos (widehat{vec{a}, vec{n}}),(widehat{vec{a}, vec{n}})<90^{circ}
]
[
sin alpha=-cos (widehat{vec{a}, vec{n}}),(widehat{vec{a}, vec{n}})>90^{circ}
]
[
sin alpha=cos (widehat{vec{a}, vec{n}}),(widehat{vec{a}, vec{n}})>0
]
[
sin alpha=-cos (widehat{vec{a}, vec{n}}),(widehat{vec{a}, vec{n}})<0
]
[
Leftrightarrow sin alpha= cos (widehat{vec{a}, vec{n}})
]
Подведем итог: синус угла между плоскостью и прямой равняется модулю косинуса угла, расположенного между вектором прямой и нормальным вектором заданной плоскости.
Угол образованный двумя векторами имеет значение скалярного произведения векторов и этих длин. При помощи формулы, приведенной ниже, можно вычислить синус угла, полученного пересечением плоскости и прямой.
[
sin alpha=operatorname{cos}(widehat{vec{a}, vec{n}}) mid=frac{(widehat{vec{a}, vec{n}}) mid}{ vec{a}|cdot vec{n}|}=frac{a_{x} cdot n_{x}+a_{y} cdot n_{y}+a_{z} cdot n_{z} mid}{sqrt{a_{z}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}
]
Все это можно привести к следующему виду:
[
alpha=arcsin frac{(widehat{vec{a}, vec{n}}) mid}{vec{a}|cdot vec{n}|}=arcsin frac{ a_{x} cdot n_{x}+a_{y} cdot n_{y}+a_{z} cdot n_{z} mid}{sqrt{a_{z}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{n_{z}^{2}+n_{y}^{2}+n_{z}^{2}}}
]
Применив основное тригонометрическое свойство, возможно вычислить косинус, но только при условии. Что синус уже известен/дан в условии задания. Как было сказано выше, угол, образованный пересечением прямой и плоскости, является острым. Это означает, что значение этого угла всегда положительно. Его можно найти формулой [alpha=sqrt{1-sin alpha}].
Для более хорошего понимания материала, рассмотрим несколько примеров и попробуем их решить.
Пример 1:
Ha векторах [overrightarrow{A B}=(1,0,2), quad overrightarrow{A C}=(-1,3,0), overrightarrow{A D}=(4,1,1)] построена пирамида.
Найдите угол между прямой AD и плоскостью ABC .
Решение:
Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямой AD является вектор [overrightarrow{A D}=(4,1,1)].
Нормальный вектор [ vec{n}] плоскости ABC перпендикулярен и вектору [overrightarrow{A B}] и вектору [overrightarrow{A C}] , то есть, в качестве нормального вектора плоскости ABC можно взять векторное произведение векторов [overrightarrow{A B}] и [ overrightarrow{A C}]:
[
vec{n}=[overrightarrow{A B} times overrightarrow{A C}]=left|begin{array}{ccc}
vec{i} & vec{j} & vec{k} \
1 & 0 & 2 \
-1 & 3 & 0
end{array}right|=-6 cdot vec{i}-2 cdot vec{j}+3 cdot vec{k} quad Leftrightarrow quad vec{n}=(-6,-2,3)
]
Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:
[
alpha=arcsin frac{mid (overrightarrow{A D}, vec{n}) mid}{|overrightarrow{A D}| cdot|vec{n}|}=arcsin frac{|4 cdot(-6)+1 cdot(-2)+1 cdot 3|}{sqrt{4^{2}+1^{2}+1^{2}} cdot sqrt{(-6)^{2}+(-2)^{2}+3^{2}}}=arcsin frac{23}{21 sqrt{2}}
]
Ответ: [arcsin frac{23}{21 sqrt{2}}]
Пример 2. Найти угол между прямой и плоскостью x-2 y+3 z+4=0.
Решение.
Из уравнения прямой найдем направляющий вектор прямой [bar{s}={2 ; 6 ;-3}].
Из уравнения плоскости найдем вектор нормали плоскости [bar{q}={1 ;-2 ; 3}].
Воспользовавшись формулой, найдем угол между прямой и плоскостью:
[
sin varphi=frac{|2 cdot 1+6 cdot(-2)+(-3) cdot 3|}{sqrt{2^{2}+6^{2}+(-3)^{2}} cdot sqrt{1^{2}+(-2)^{2}+3^{2}}}=frac{|2-12-9|}{sqrt{4+36+9} cdot sqrt{1+4+9}}=frac{|-19|}{sqrt{49} cdot sqrt{14}}=frac{19}{7 sqrt{14}}
]
Ответ: [sin varphi=frac{19}{7 sqrt{14}} ].
Дополнительные теоремы
- Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
- Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
- Если прямая параллельна плоскости, то угол между ней и плоскостью М считается равным нулю. Если прямая перпендикулярна прямой, т.е. равен 90 градусам.
- Чтобы найти синус угла между прямой и плоскостью можно сначала вычислив косинус угла между прямой и перпендикуляром к плоскости.
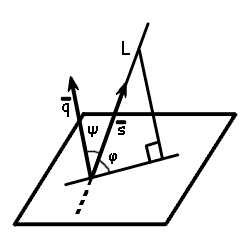
- Если в пространстве заданы направляющий вектор прямой L s = {l; m; n} и уравнение плоскости Ax + By + Cz + D = 0, то угол между этой прямой и плоскостью можно найти, используя следующую формулу:
[
sin varphi=frac{|A cdot 1+B cdot m+C cdot n|}{sqrt{A^{2}+B^{2}+C^{2}} cdot sqrt{1^{2}+m^{2}+n^{2}}}
]
Угол между прямой и плоскостью
Навигация по странице:
- Определение угла между прямой и плоскостью
- Формула для вычисления угла между прямой и плоскостью
- Вывод формулы вычисления угла между прямой и плоскостью
- Примеры задач на вычисление угла между прямой и плоскостью
Определение.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Формула вычисления угла между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L
s = {l; m; n}
и уравнение плоскости
Ax + By + Cz + D = 0,
то угол между этой прямой и плоскостью можно найти используя формулу
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Пример вычисления угла между прямой и плоскостью
Пример 1.
Найти угол между прямой
| x – 4 | = | y + 2 | = – | z – 6 |
| 2 | 6 | 3 |
и плоскостью x – 2y + 3z + 4 = 0.
Решение.
Из уравнения прямой найдем направляющий вектор прямой
s = {2; 6; -3}
Из уравнения плоскости найдем вектор нормали плоскости
q = {1; -2; 3}
Воспользовавшись формулой, найдем угол между прямой и плоскостью
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
=
| 2 – 12 – 9 |√4 + 36 + 9 · √1 + 4 + 9
=
|-19|√49 · √14
=
197√14
Ответ: sin φ = 197√14.