Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
Скрещивающиеся прямые – не параллельны, не имеют общих точек, не пересекаются.
Признаки Скрещивающихся прямых
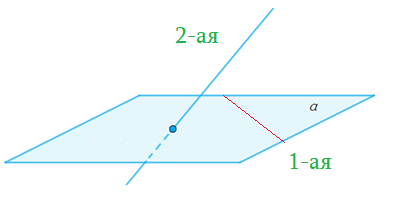
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
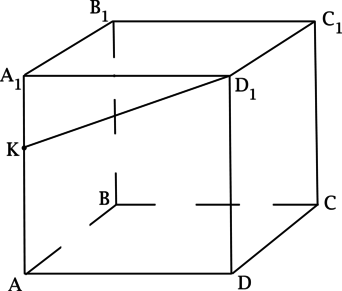
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов – прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней – прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ – плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I 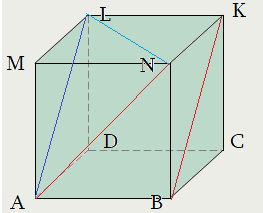
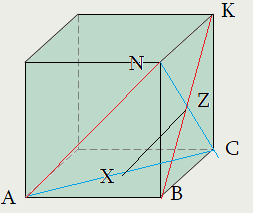
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ – середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость “скольжения” – плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно “как стержень”. Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ – именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: – увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ – плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол – это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ – плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2 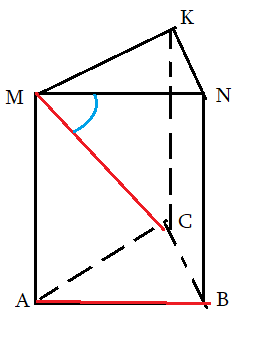
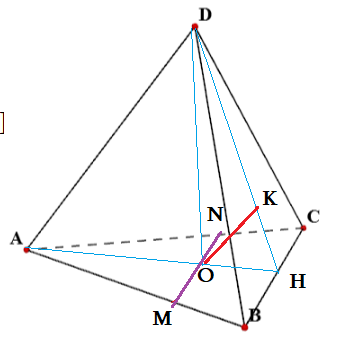
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим “движениями” наши прямые в точку $O$ – основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ – пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ – высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, “взамен” наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ – плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
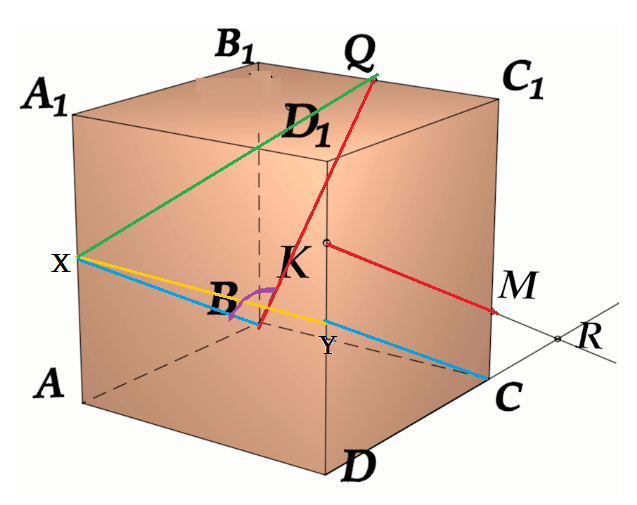
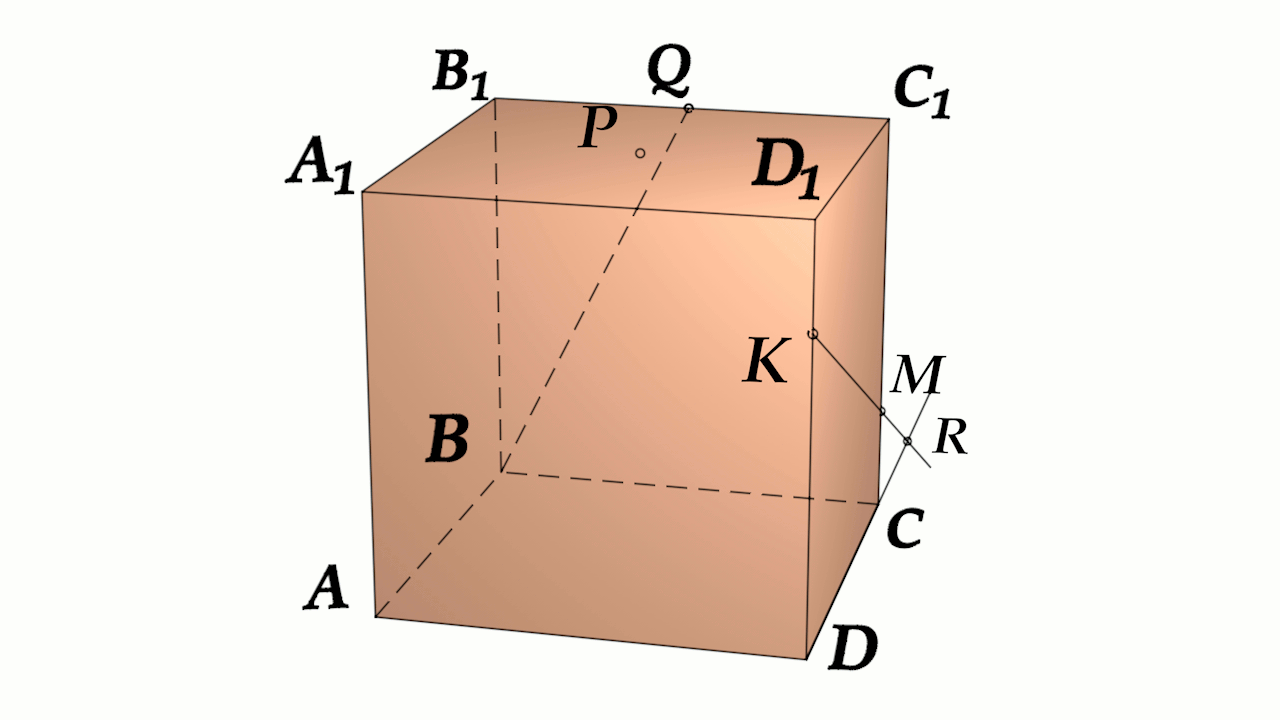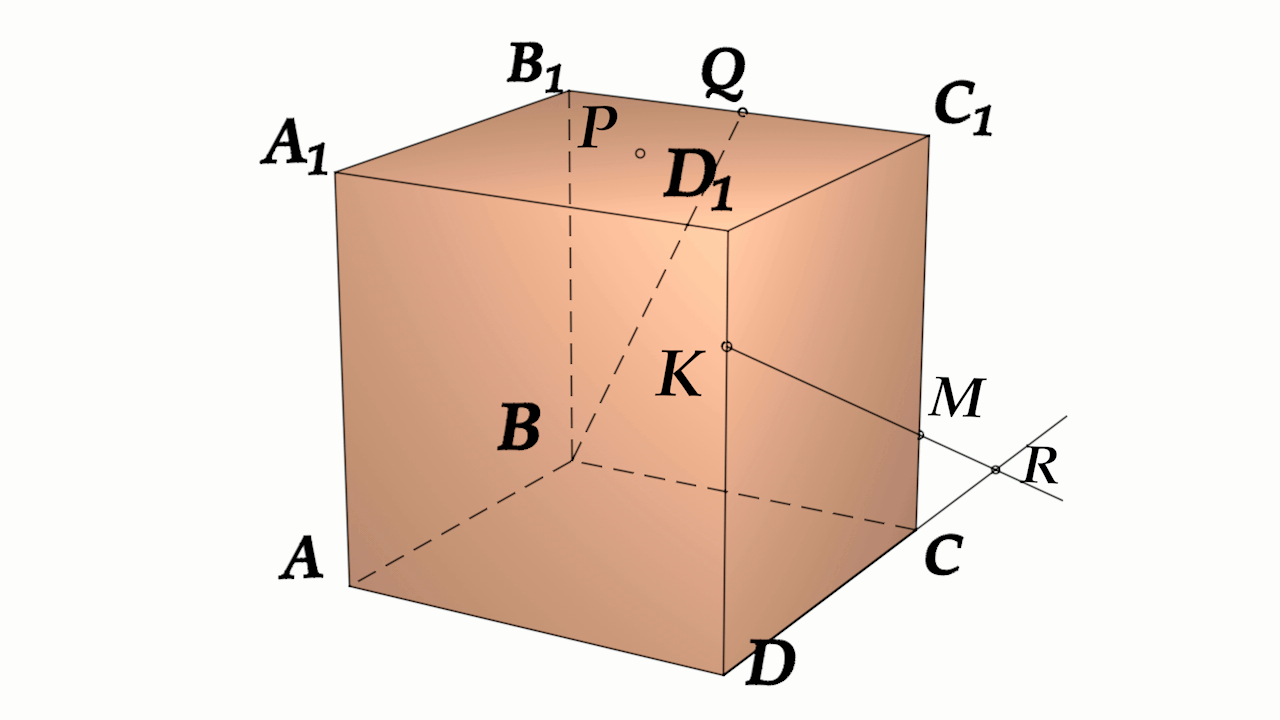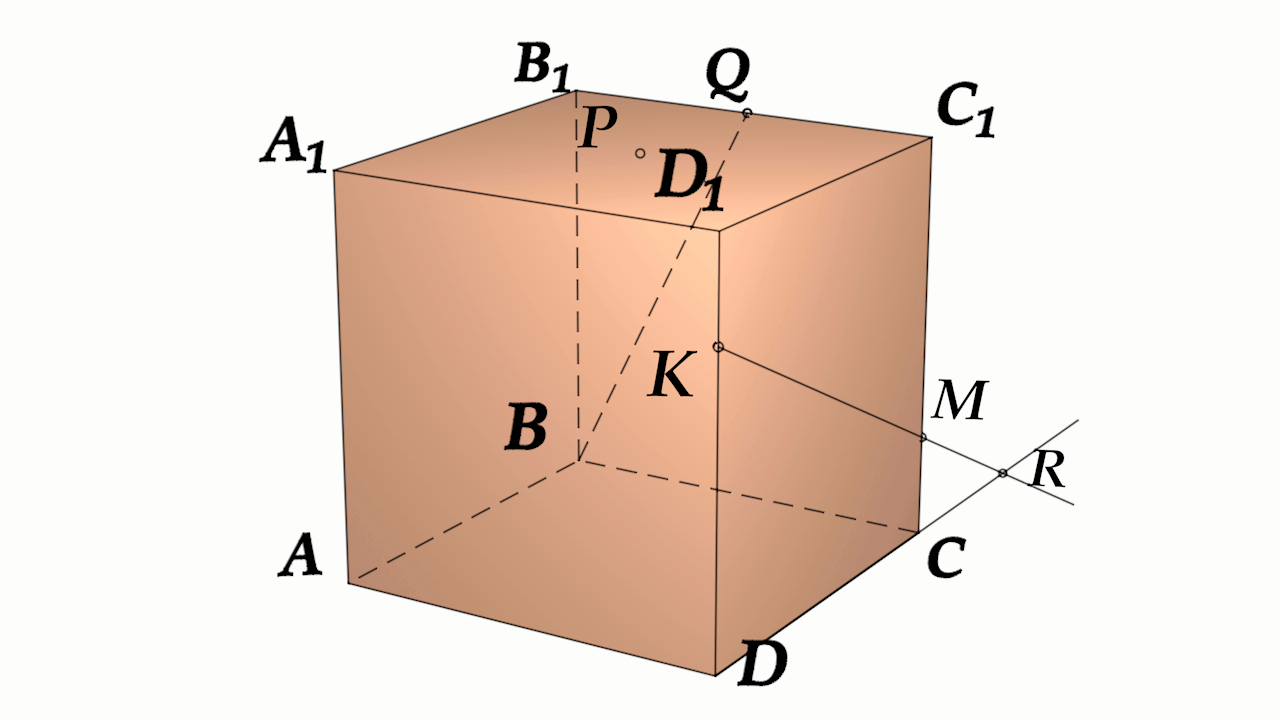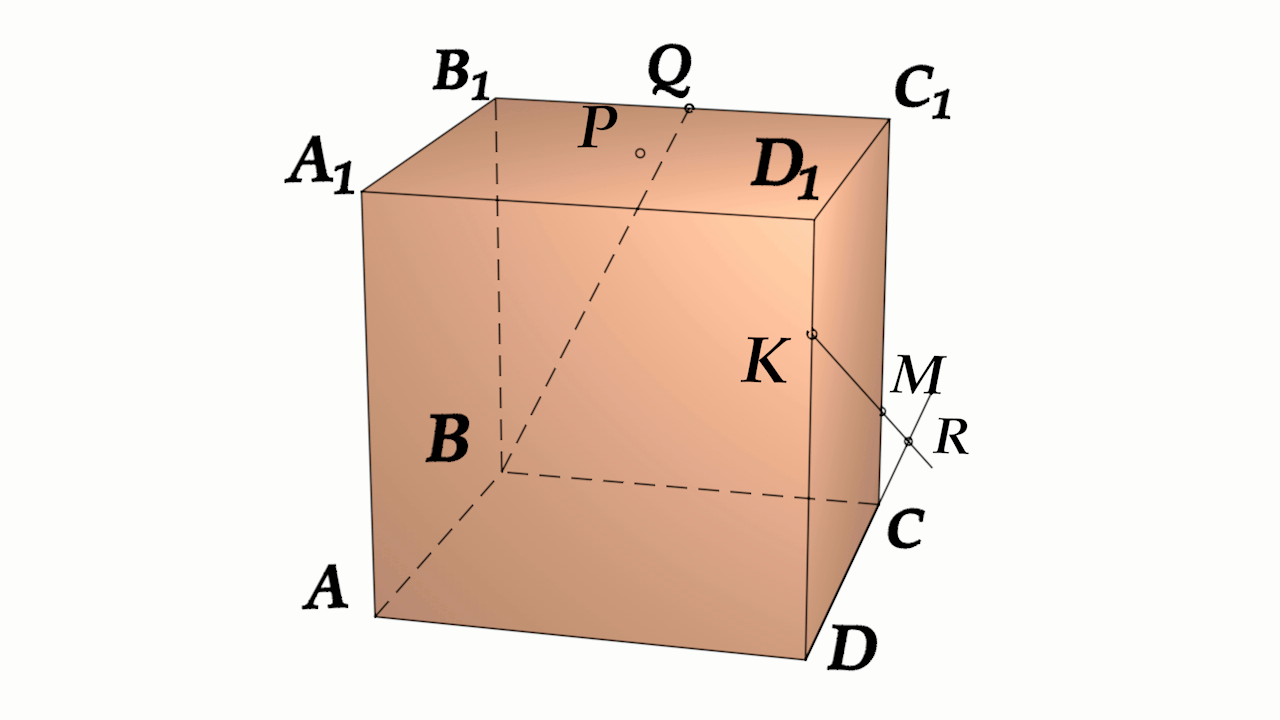
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ – середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .

- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ – плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
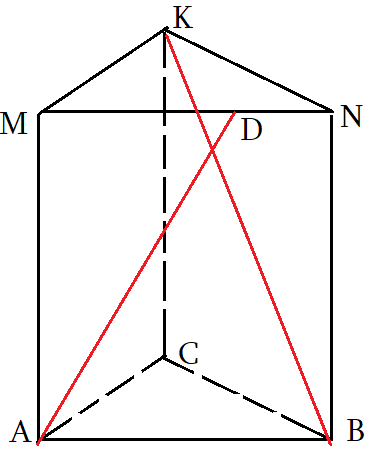
- Чтоб найти угол между скрещивающимися прямыми, нужно “подвигать параллельно” $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ – т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
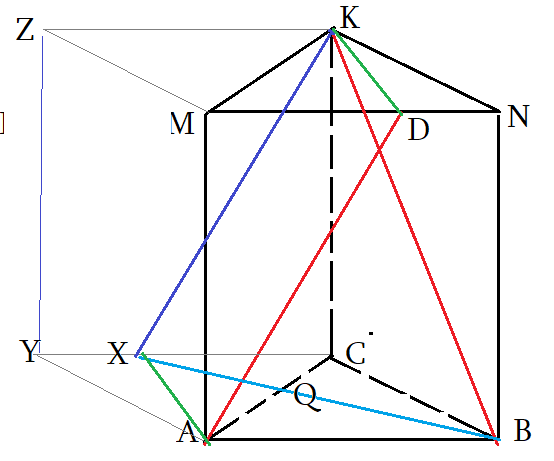
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, “движения”, плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ – то что надо!
- Признак: $XKB$ – плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения:
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
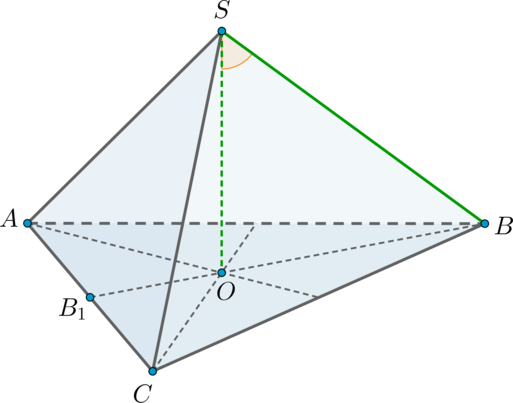
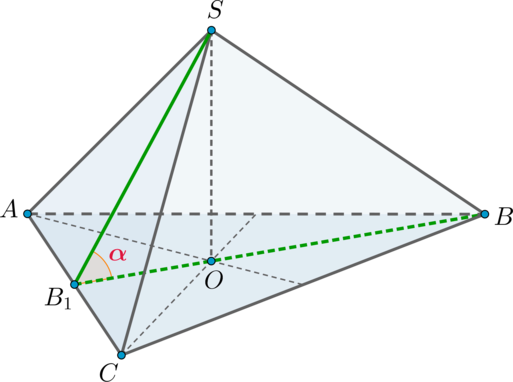
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
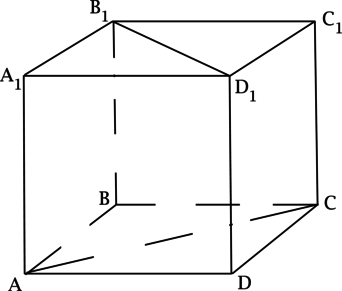
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
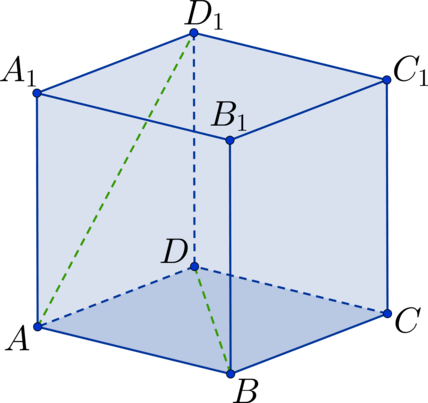
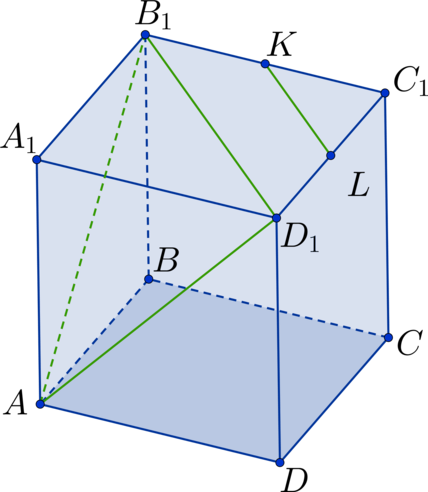
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
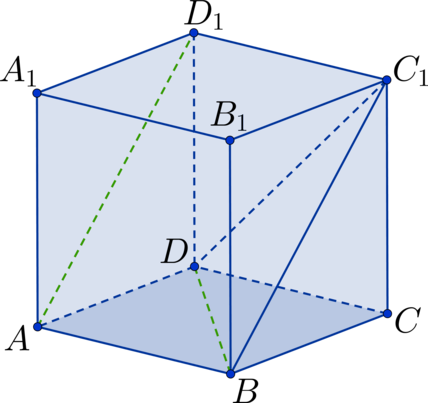
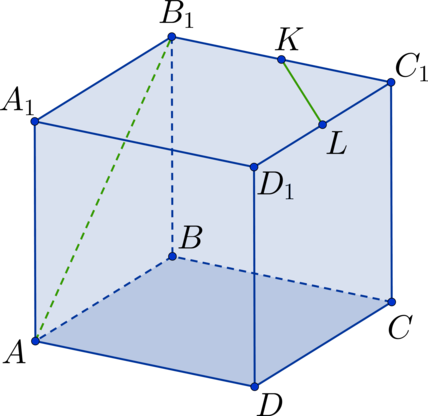
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
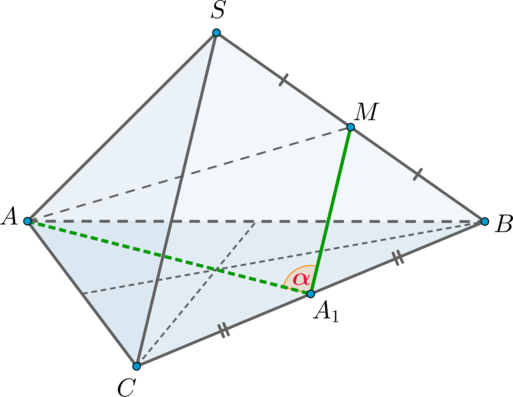
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».

УСТАЛ? Просто отдохни
Скрещивающиеся прямые
Как определяется угол между скрещивающимися прямыми?
Ты можешь спросить, а чего тут определять? Угол, он и в Африке (то есть в пространстве) – угол!
И действительно, если прямые лежат в одной плоскости, то угол между ними ищется так же, как и на плоскости:
Наименьший из двух углов, образованных при пересечении.
Но что же делать, если прямые совсем не пересекаются?
Читай эту статью и всё узнаешь!
Скрещивающиеся прямые — коротко о главном
Если прямые лежат в разных плоскостях (т.е. не пересекаются), нужно через произвольную точку на одной прямой (например, прямая ????) провести прямую, параллельную другой прямой (например, прямую ????′, где ????′||????.
Скрещивающиеся прямые — подробнее
Как найти угол, если прямые не пересекаются?
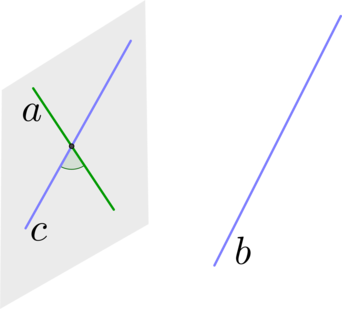
Вот, например: прямые ( displaystyle a) и ( displaystyle b) скрещиваются. Какой угол между ними?
Чтобы это определить, делаем так: через произвольную точку одной прямой (например ( displaystyle b)), нужно провести прямую ( displaystyle {a}’||a).
И тогда угол между ( displaystyle a) и ( displaystyle b) будет равен (по определению!) углу между ( displaystyle {{a}’}) и ( displaystyle b).
Да, но как это применить в задачах? Давай посмотрим.
Решение задач на угол между скрещивающимися прямыми
В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) найти угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}).
Решаем:
Прямые ( displaystyle AC) и ( displaystyle D{{C}_{1}}) не пересекаются, но нужно как-то найти угол между ними.
Пользуемся правилом: через точку ( displaystyle {{C}_{1}}) проведем прямую ( displaystyle {{A}_{1}}{{C}_{1}}). Она будет параллельна ( displaystyle AC).
Значит, угол между ( displaystyle AC) и ( displaystyle D{{C}_{1}}) равен углу между ( displaystyle {{A}_{1}}{{C}_{1}}) и ( displaystyle D{{C}_{1}}). Осталось его найти.
Смотри: ( displaystyle {{A}_{1}}{{C}_{1}}), ( displaystyle {{A}_{1}}D) и ( displaystyle D{{C}_{1}}) – диагонали граней куба, поэтому ( displaystyle {{A}_{1}}{{C}_{1}}={{C}_{1}}D={{A}_{1}}D), то есть ( displaystyle Delta {{A}_{1}}{{C}_{1}}D) – равносторонний.
Поэтому ( displaystyle angle {{A}_{1}}{{C}_{1}}D=60{}^circ ).
Ответ: ( displaystyle 60{}^circ ).
Бонус: Вебинар из нашего курса подготовки к ЕГЭ по математике
Задачи на скрещивающиеся прямые и углы между ними попадаются сплошь и рядом в этом вебинаре.
ЕГЭ 8. Куб. Параллелепипед. Призма – расстояния и углы в пространстве
На этом уроке мы на примере самых простых объемных фигур научимся находить важнейшие вещи в стереометрии — расстояния и углы в пространстве.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
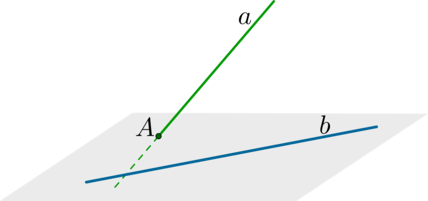
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
На каких материалах репетитор по математике строит работу с темой: углы между прямыми
Предлагаю познакомиться некоторыми авторскими дидактическими материалами в рамках темы «углы между скрещивающимися прямыми». Обычно репетитор по математике использует на своих уроках стандартные номера из учебника, в которых информация об искомых объектах предоставляется в форме длинных текстов: в прямоугольном параллелепипеде с размерами … проведены прямые MN и KP так, что … Если репетитор по математике работает с невнимательным учеником, который не воспринимает текстовую информацию, путается в переносе условия на рисунок, то единственным выходом может стать методика визуальных заданий. Она особенно эффективна при изучении темы «углы между прямыми и плоскостями» в пространстве (стереометрия).
Уже несколько лет я работаю с собственными методическими разработками, и не обращаюсь за помощью ни к каким задачникам и пособиям. Некоторые задания из своей базы я предлагаю для ознакомления.
Как репетитор по математике подает задания ученику?
Все визуальные номера снабжены минимальной текстовой информацией и сопровождаются обязательными рисунками. Все данные условий находятся на этих рисунках. Для того, чтобы собрать внимание ученика на отработке определенного навыка (например, на поиске углов между различными прямыми в кубе) задачи разбиты на блоки:
1) поиск углов в кубе
2) поиск углов в правильных пирамидах: а) в треугольных б) четырехугольных в) шестиугольных.
Решаются они также блоками. Одна часть разбирается с репетитором непосредственно на занятии, а вторая часть задается дом. Я не стал оформлять страничку с разделением номеров для совместной и домашней работы, ибо это разделение, как и точный подбор задач, всецело зависит от конкретного ученика и от конктерной ситуации в которой находится репетитор (временной, учебной, методической, психологической…)
Как репетитор по математике выделяет прямые для поиска угла?
Линии во всех номерах, между которыми надо найти угол выделяются красным цветом. В таком случае у репетитора по математике отпадает необходимость формулировать вопрос к каждой задаче. Перед его учеником стоит одна и так же цель при разных геометрических расположениях прямых линий. Так проще концентрироваться на поиске самого алгоритма. Согласитесь, что это удобно. И не только для ученика.
Расположение точек, через которые проведены прямые, репетитор по математике выбирает самым простейшим образом. Обычно это или вершины многогранника, рили середины его ребер. В последнем случае репетитору достаточно показать черточками равные половинки этих ребер.
Задачи на нахождение углов между скрещивающимися прямыми
На этой страничке представлены образцы задач только с использованием куба и его элементов. Аналогичные материалы имеются в моей базе задач и на пирамиды.
Найдите углы между красными прямыми:
Все номера решаются по одной и той же системе. Напомню, что угом между скрещивающимися прямыми называется острый угол между любыми прямыми, которые или совпадают с имеющимися или параллельны им. Поэтому требуется параллельно сдвинуть одну из прямых (или обе) так, чтобы получить из них треугольник с удобными сторонами. Далее ребро куба обозначается какой-нибудь буквой и через нее выражаются стороны этого треугольника. Если репетитор по математике объяснит уче6нику, что величины углов не зависят от того, в чем измеряются длины отрезков (ребер), то он будет вправе вводить для каждой задачи свою мерку (единицу), удобную для решения. Для задач с серединами в качестве такой мерки лучше взять половину ребра куба.
Эти материалы подойдут для того случая, если репетитором проводится целенаправленная комплексная подготовка к ЕГЭ по математике на базе задачи С2. Возможны более сложные сочетания линий. Тогда на помощь репетитору приходит метод координат. Один из моих учеников наловчился пристраивать к кубу точно такой же куб и сдвигать прямые, размещая их внутри этого вспомогательного куба. Я не советую заниматься подобным творчеством, ибо рисунок сильно усложняется. Всегда можно как-то устроить перемещения внутри исходного куба. Или, в крайнем случае, воспользоваться методом координат:
Вводится система координат (в кубе это сделать проще всего), выбирается единица измерения, о которой я уже сказал выше, и векторы, имеющие направления данных прямых. Находим модуль их скалярного произведения и делим его на произведение длин векторов. Если в ответ нужно записать сам угол, то он будет равен арккосинусу того, что получилось.
Колпаков А.Н. Репетитор по математике — автор заданий. Москва.