В статье рассматриваются определения угла между скрещивающимися прямыми с приведением графических иллюстраций. При имеющихся координатах направляющих векторов заданных прямых научимся находить искомый угол. В заключительной части решим задачи на нахождение угла.
Угол между скрещивающимися прямыми – определение
Для нахождения искомого угла необходимо пройти несколько этапов.
Две прямые в трехмерном пространстве называются скрещивающимися в случае, если они не находятся в одной плоскости.
Из определения о скрещивающихся прямых следует, что они не являются параллельными или пересекающимися и не совпадают, тогда они находились бы в одной и той же плоскости.
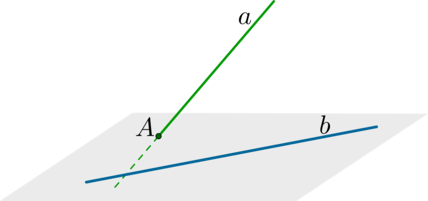
Рассмотрим рисунок, приведенный ниже.
В трехмерном пространстве имеются скрещивающиеся прямые a и b. Проведем прямые а1 и b1 параллельные скрещивающимся a и b. Точка М1 является точкой пространства, через которую они проходят. Отсюда получаем, что а1 и b1 являются пересекающимися прямыми.
Обозначим угол между a1 и b1 равным значению α. Построение прямых a2 и b2 параллельно скрещивающимися относительно a и b в точке М2 отличной от М1 приводит к тому, что значение угла между ними обозначим как α. То есть угол между прямыми a1 и b1 равен углу между a2 и b2. В этом можно убедиться, если про/извести параллельный перенос. Тогда точки М1 и М2 совпадают.
Углом между скрещивающимися прямыми называют угол, который образуется между двумя параллельными заданными скрещивающимися прямыми.
Отсюда следует, что угол не зависит от точки M и ее выбора. Поэтому точка M может быть любой. Рассмотрим рисунок, приведенный ниже.
Нахождение угла между скрещивающимися прямыми
Угол между скрещивающимися прямыми определяется через угол пересекающихся прямых. Поиск угла сводится к его нахождению между пересекающимися прямыми пространства. Школьные методы решения основываются на необходимости построения на основе подобия фигур или теоремах косинуса, что позволит определить синус, косинус, тангенс угла прямоугольного треугольника.
Удобным способом решения считается нахождение угла методом координат. Рассмотрим его.
Трехмерное пространство имеет прямоугольную систему координат Охуz. Имеется задача, в которой необходимой найти угол α, образованный скрещивающимися прямыми a и b с заданными уравнениями прямых в пространстве.
Для решения необходимо взять произвольную точку в трехмерном пространстве и обозначить буквой M, что дает понять, через нее проходят прямые a1 и b1, которые параллельны скрещивающимся a и b. Угол α , образованными прямыми a и b, из этого определения получится равным пересекающимся a1 и b1.
Для нахождения искомого угла между a1 и b1 необходимо использовать формулу для нахождения угла между пересекающимися прямыми, а для этого нужно знать значение координат направляющих векторов у прямых a1 и b1.
Для их получения необходимо применить определение направляющего вектора, которое говорит о том, что множества векторов совпадают. Направляющие векторы прямых обозначают a→=(ax, ay, az) и b→=(bx, by, bz).
Векторы a→ и b→ имеют координаты, определяющиеся из условия по уравнению или по координатам точек пересекающихся прямых. Тогда получаем, что угол между двумя скрещивающимися прямыми a и b вычисляется из формулы α=arccosa→, b→a→·b→=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2, а a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Использование формулы для нахождения косинуса угла между скрещивающимися прямыми а и b дает выражение вида cos α=a→, b→a→·b→=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2.
При помощи основного тригонометрического тождества можно найти синус угла между этими прямыми при известном косинусе из формулы sin α=1-cos2 α.
Найти угол между скрещивающимися прямыми a и b, которые заданы уравнениями x2=y-40=z+1-3 и x=1+λy=1-λz=-3+4·λ, λ∈R и определяются в системе координат Охуz.
Решение
Для определения координат необходимо использовать каноническое уравнение прямой в плоскости. необходимо обратить внимание на знаменатель дробей. Отсюда видно, что a→=(2, 0, -3) является направляющим вектором прямой x2=y-40=z+1-3. При наличии параметрического уравнения можно определить координаты направляющего вектора, так как она равняются коэффициентам, тогда получаем, что b→=(1, -1, 4) является направляющим вектором для прямой вида x=1+λy=1-λz=-3+4·λ, λ∈R.
Отсюда получаем, что имеются все необходимые формулы и данные для того, чтобы произвести вычисление угла между скрещивающимися прямыми. Имеем, что
α=arccosax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2=arccos2·1+0·(-1)+(-3)·422+02+(-3)2·12+(-1)2+42==arccos1013·18=arccos10326
Ответ: угол между скрещивающимися прямыми равен arccos10326.
Найти значение синуса и косинуса угла между скрещивающимися прямыми, где имеются ребра AD и ВС, принадлежащие пирамиде ABCD, с известными вершинами с координатами A(0, 0, -1), B(5, 7, -5), C(3, 7, -5), D(1, 3, 1).
Решение
AD→ и BC→ являются векторами соответствующих сторон заданной фигуры. Необходимо вычислить координаты с помощью имеющихся данных начала и конца.
Получаем, что AD→=(1-0, 3-0, 1-(-1))⇔AD→=(1, 3, 2)BC→=(3-5, 7-7, -5-(-3))⇔BC→=(-2, 0, -2)
Из формулы cos α=arccosAD→, BC→AD→·BC→ находим косинус угла между заданными скрещивающимися прямыми. Получаем выражение вида
cos α=1·(-2)+3·0+2·(-2)12+32+22·(-2)2+02+(-2)2=614·8=327
Перейдем к вычислению синуса угла между этими прямыми. Подставляем значения и получаем, что sin α=1-cos2α=1-3272=1927.
Ответ: sin α=1927, cos α=327.
В заключительном этапе рассмотрим задачу, в которой нужно найти угол между скрещивающимися прямыми с самостоятельно введенной системой координат.
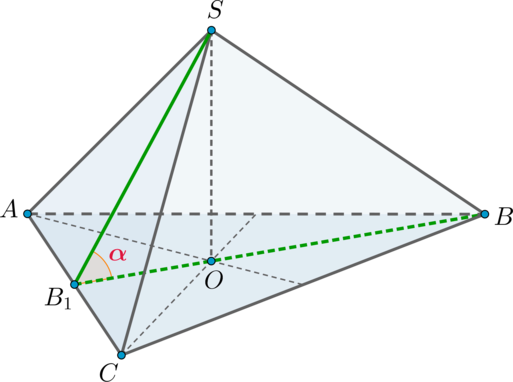
Имеется прямоугольный параллелепипед ABCDA1B1C1D1 со сторонами АВ=3, АD=2 и AA1=7 единиц. Точка E делит прямую АА1 как 5:2. Определить угол между скрещивающимися прямыми ВЕ и А1С.
Решение
Ребра заданного параллелепипеда являются взаимно перпендикулярными, поэтому необходимо ввести прямоугольную систему координат для определения угла между указанными скрещивающимися прямыми с помощью метода координат.
Для начала вводится прямоугольная система координат Охуz. Получаем, что начало координат является совпадающим с вершиной A, а Ох совпадает с прямой AD, Оу с AB, а Оz с АА1. Рассмотрим рисунок, приведенный ниже.
Отсюда имеем, что точка B с координатами (0, 3, 0), E – (0, 0, 5), AА – (0, 0, 7), C – (2, 3, 0). Исходя из координат, мы можем получить координаты векторов BE→ и A1C→, необходимые для дальнейшего решения задачи. Получаем, что BE→=(0, -3, 5), A1C→=(2, 3,-7).
Применим формулу для нахождения угла, образованного скрещивающимися прямыми, при помощи координат направляющих векторов. Получаем выражение вида
α=arccosBE→, A1C→BE→·A1C→=arccos0·2+(-3)·3+5·(-7)02+(-3)2+52·22+32+(-7)2==arccos4434·62=arccos22527
Ответ: arccos22527.
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
Скрещивающиеся прямые – не параллельны, не имеют общих точек, не пересекаются.
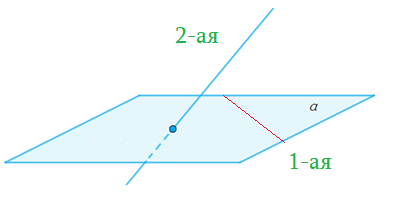
Признаки Скрещивающихся прямых
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов – прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней – прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ – плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I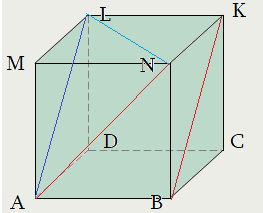 
case II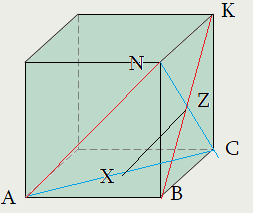 
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ – середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость “скольжения” – плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно “как стержень”. Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ – именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: – увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ – плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол – это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ – плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2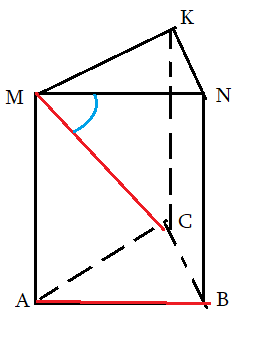 
к задаче 3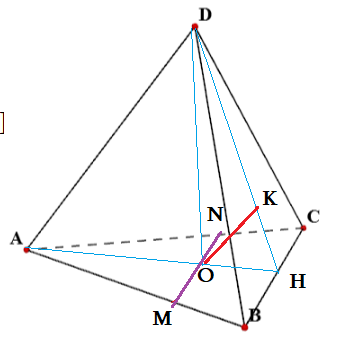 
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим “движениями” наши прямые в точку $O$ – основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ – пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ – высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, “взамен” наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ – плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
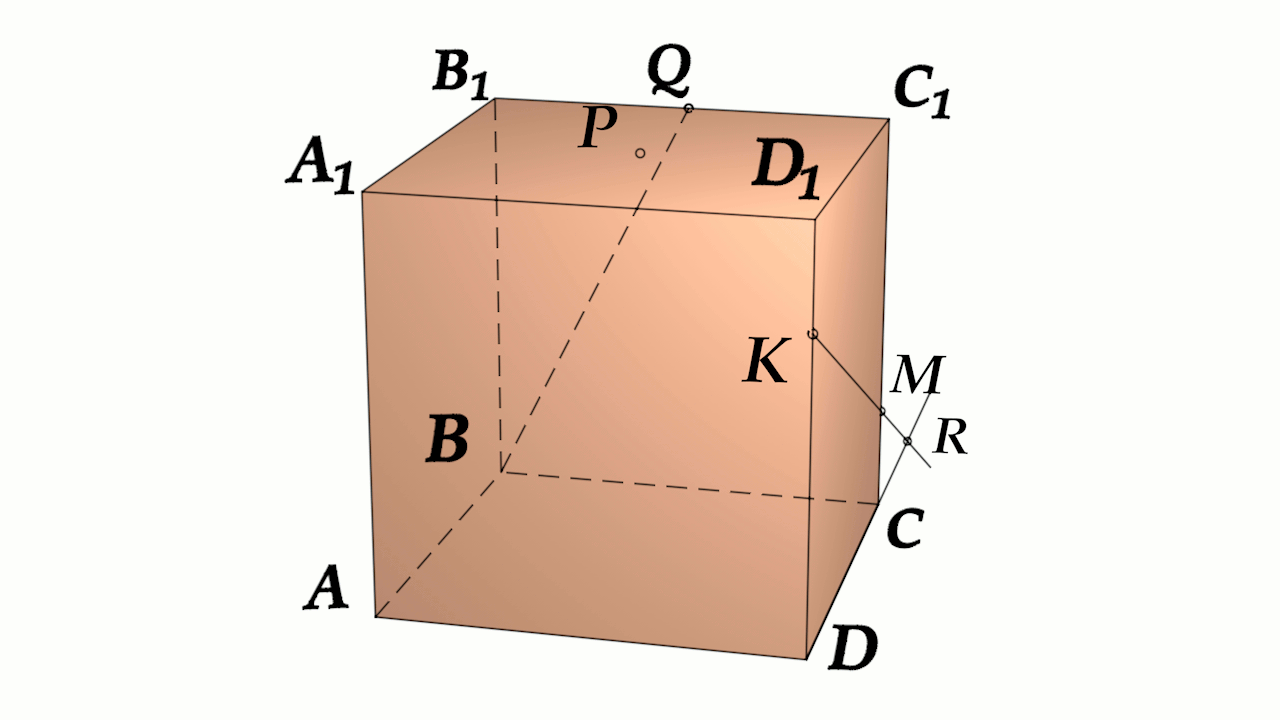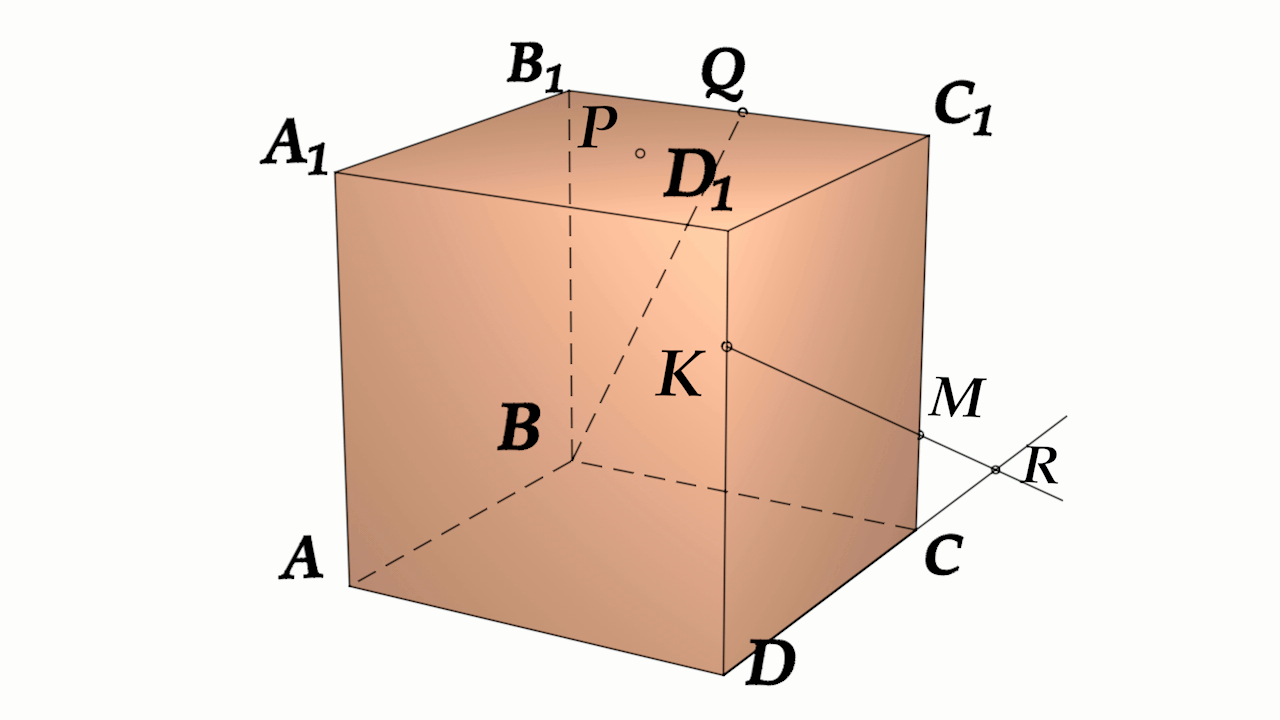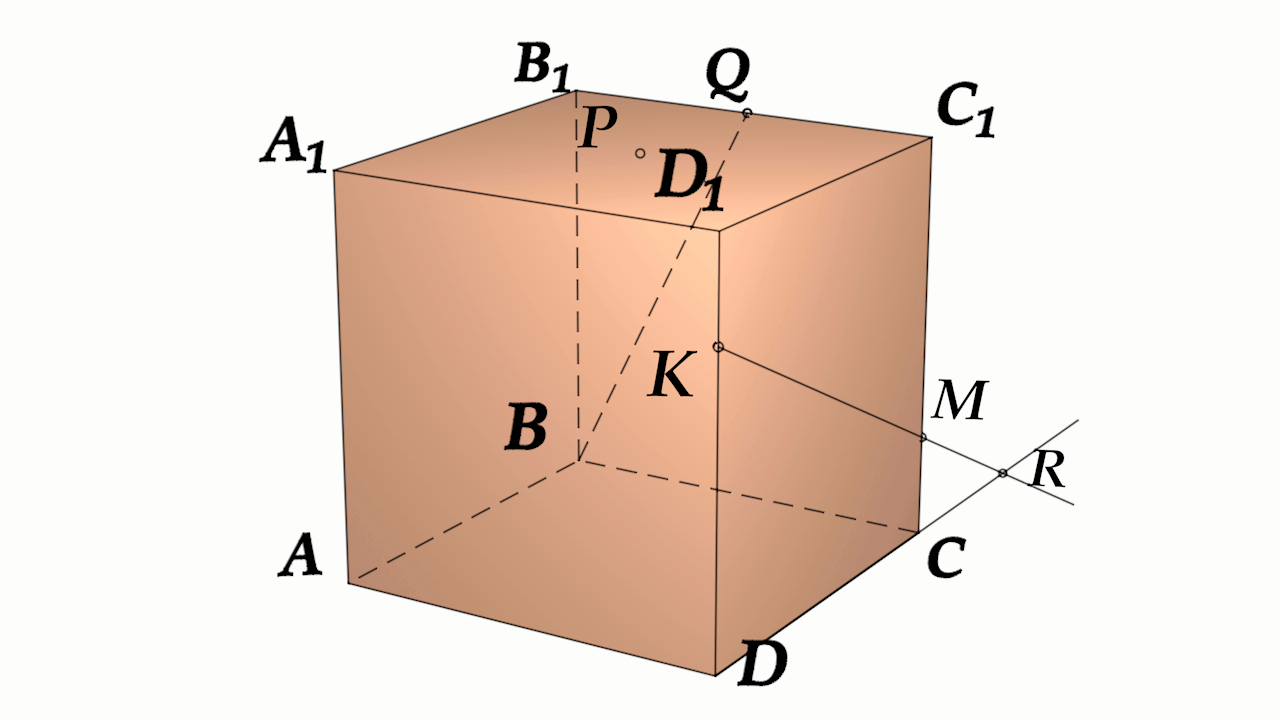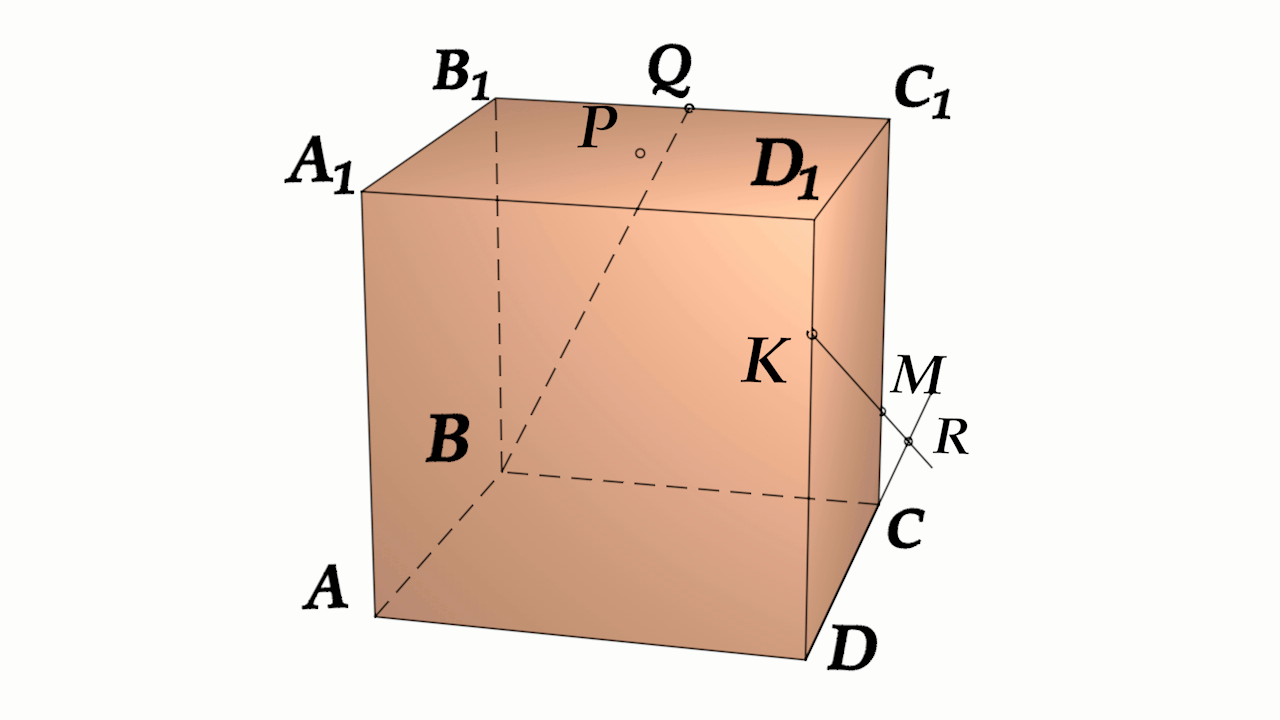
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ – середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .
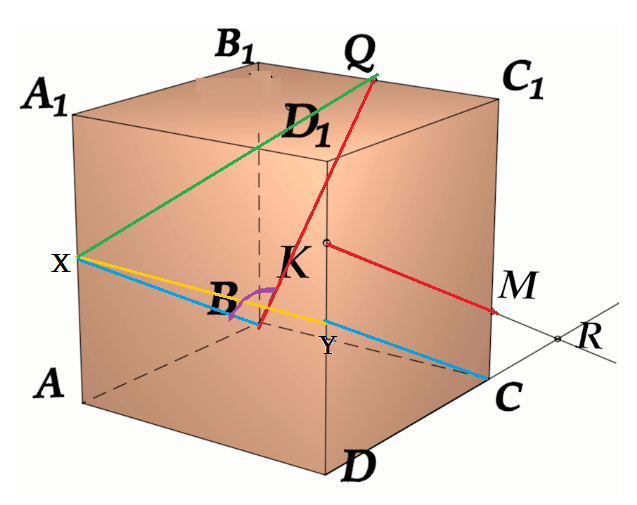
- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ – плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
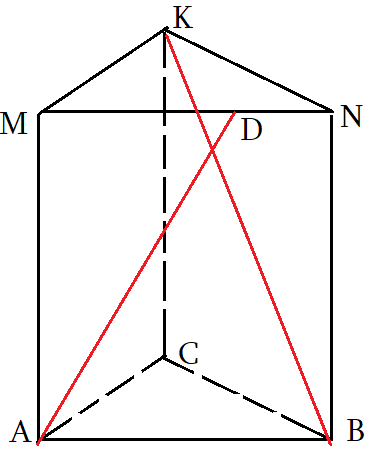
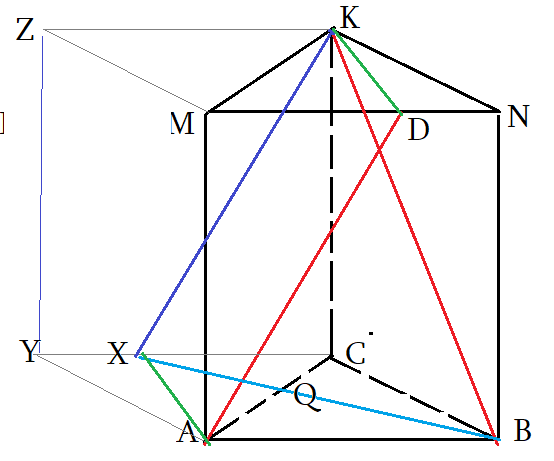
- Чтоб найти угол между скрещивающимися прямыми, нужно “подвигать параллельно” $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ – т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, “движения”, плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ – то что надо!
- Признак: $XKB$ – плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения:
Прямоугольный параллелепипед
Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.
На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.
Свойства прямоугольного параллелепипеда:
- В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
- Противоположные грани попарно равны и параллельны.
- Все двугранные углы прямоугольного параллелепипеда – прямые.
- Диагонали прямоугольного параллелепипеда равны.
- Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы были понятны формулы, введем обозначения:
$с$ – высота(она же боковое ребро);
$P_<осн>$ – периметр основания;
$S_<осн>$ – площадь основания;
$S_<бок>$ – площадь боковой поверхности;
$S_<п.п>$ – площадь полной поверхности;
$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.
$S_<бок>=P_<осн>·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.
Дополнительные сведения, которые пригодятся для решения задач:
$а$ – длина стороны.
$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.
Пирамида
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.
Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.
Объем любой пирамиды равен трети произведения основания и высоты.
В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/<2>$, где $h_a$ – высота, проведенная к стороне $а$.
- $S=/<2>$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√$, где $р$ – это полупериметр $p=/<2>$.
- $S=p·r$, где $r$ – радиус вписанной окружности.
- $S=/<4R>$, где $R$ – радиус описанной окружности.
- Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ – катеты прямоугольного треугольника.
- Для равностороннего треугольника $S=/<4>$, где $а$ – длина стороны.
В основании лежит четырехугольник.
- Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны. - Ромб.
$S=/<2>$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами. - Трапеция.
$S=<(a+b)·h>/<2>$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции. - Квадрат.
$S=a^2$, где $а$ – сторона квадрата.
Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.
Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.
Объем пирамиды, в основании которой лежит прямоугольник
Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.
В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.
Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Прямоугольный параллелепипед. Что это такое?
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
- Противолежащие грани параллелепипеда равны и параллельны друг другу.
- Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Параллелепипед симметричен относительно середины его диагонали.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
- Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
- Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
- Высота прямого параллелепипеда равна длине бокового ребра.
- Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
- Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
- Площадь боковой поверхности прямого параллелепипеда
Sб = Ро*h
Ро — периметр основания
h — высота - Площадь полной поверхности прямого параллелепипеда
Sп = Sб+2Sо
Sо — площадь основания - Объем прямого параллелепипеда
V = Sо*h
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
- Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
- Противолежащие грани параллелепипеда попарно параллельны и равны.
- Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
- Диагонали прямоугольного параллелепипеда равны.
- В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
- Любая грань прямоугольного параллелепипеда может быть принята за основание.
- Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).
Формулы прямоугольного параллелепипеда:
- Объем прямоугольного параллелепипеда
V = a · b · h
a — длина, b — ширина, h — высота - Площадь боковой поверхности
Sбок = Pосн·c=2(a+b)·c
Pосн — периметр основания, с — боковое ребро - Площадь поверхности
Sп.п = 2(ab+bc+ac)
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = d₁² + c² = a² + b² + c²
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
- В кубе 6 граней, каждая грань куба — квадрат.
- Противолежащие грани параллельны друг другу.
- Все углы куба, образованные двумя гранями, равны 90°.
- У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
- Диагонали куба равны.
- Диагональ куба в √3 раз больше его ребра.
- Диагональ грани куба в √2 раза больше длины ребра.
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
- Объем куба через длину ребра a
V = a3 - Площадь поверхности куба
S = 6a2 - Периметр куба
P = 12a
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a – длина, b – ширина, c – высота. Тогда a = 10, b = 5, c = 8.
Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) – сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) – суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) – сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) – сумма длин всех ребер прямоугольного параллелепипеда.
Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X – сумма длин ребер).
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°.
По теореме Пифагора:
BD1 2 = DD1 2 + BD 2
BD 2 = BD1 2 – DD1 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 – AD 2 = (√17)2 — 4 2 = 1
A1B1 = AB = 1.
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
- прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
- параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
- основание прямоугольного параллелепипеда — прямоугольник;
- три измерения прямоугольного параллелепипеда: длина, ширина, высота;
- диагональ параллелепипеда равна сумме квадратов его измерений.
Стереометрия. Страница 5
- Главная
- Репетиторы
- Учебные материалы
- Контакты
1. Двугранный, трехгранный углы
Двугранный угол представляет собой фигуру, образованную двумя полуплоскостями и общей ограничивающей их прямой. Полуплоскости называются гранями двугранного угла, а прямая, ограничивающая их, – ребром (Рис.1).
Если провести плоскость, перпендикулярную ребру двугранного угла, то она пересечет его грани по двум полупрямым. Угол, образованный между двумя этими полупрямыми, называется линейным углом двугранного угла.
Градусная мера двугранного угла равна градусной мере линейного угла. Величина двугранного угла не зависит от выбора линейного угла, т.е. плоскости, перпендикулярной ребру двугранного угла.
7. Правильные многогранники
Если выпуклый многогранник имеет все грани правильные многоугольники с равным числом сторон и в каждой вершине многоугольника сходится одно и то же число ребер, то такой многогранник называется правильным.
Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.
Тетраэдр это многогранник, у которого грани правильные треугольники.
Куб это многогранник, у которого все грани – квадраты.
Октаэдр – многогранник, который представляет собой две пирамиды с общим основанием. Основание этих пирамид – квадрат.
Додекаэдр это многогранник, у которого грани правильные пятиугольники. В каждой вершине сходится по три ребра.
Икосаэдр это многогранник, у которого грани правильные треугольники. В каждой вершине сходится по пять ребер.
8. Пример 1
Докажите, что сечение призмы, параллельное основаниям, равно основаниям.
Доказательство:
Пусть дана призма АВСA’B’C’ (Рис.7). Основания призмы равны и являются треугольниками. Они лежат в параллельных плоскостях и совмещаются параллельным переносом. Отсюда следует, что боковые ребра параллельны и равны.
Если провести плоскость α, параллельную основаниям, то в сечении получится такое же основание. Так как сторона A”C” параллельна АС, A”B” – AB, B”C” – BC. А так как боковые ребра AA’, BB’, CC’ параллельны, то АА”C”C, AA”B”B, BB”C”C прямоугольники (параллелограммы, если АВСA’B’C’ наклонная призма).
Отсюда следует, что A”C” = AC, A”B” = AB, B”C” = BC. Таким образом, треугольник A”B”C” равен треугольнику АВС и A’B’C’ соответственно. Отсюда можно сделать и общий вывод: если в основании призмы будет лежать како-либо многоугольник, то в сечении, параллельном основаниям, получится такой же многоугольник.
Рис.7 Задача. Докажите, что сечение призмы.
Пример 2
Боковое ребро наклонной призмы равно 16 м. Оно наклонено к плоскости основания под углом 30°. Найдите высоту призмы.
Решение:
Пусть дана наклонная призма АВСA’B’C’ (Рис. 8). Рассмотрим нижнее основание – треугольник АВС. Проведем прямую а через точку А в плоскости основания, перпендикулярную A’A. Проведем также прямую АР, перпендикулярную прямой а. Таким образом, прямая АР является проекцией наклонной A’A на плоскость основания. А плоскость, в которой лежит треугольник AA’P, перпендикулярна плоскости основания.
Рассмотрим треугольник AA’P. Угол A’AP равен 30° по условию задачи. Опустим высоту A’O. В прямоугольном треугольнике AA’O найдем A’O.
sin 30° = A’O / AA’ . Отсюда:
A’O = AA’ sin 30° = 16 / 2 = 8 м.
Рис.8 Задача. Боковое ребро наклонной призмы равно 15 м.
Пример 3
В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковые ребра и наклоненная к плоскости основания под углом 60°. Сторона основания равна 8 м. Найдите площадь полученного сечения.
Решение:
Пусть дана правильна четырехугольная призма АВСDA’B’C’D’ (Рис. 9). Заметим, что многоугольник PBCDF является проекцией многоугольника PKHSF на плоскость основания, площадь которого необходимо найти. Следовательно, найдем площадь многоугольника PBCDF.
SPBCDF = 8 2 – (8/2) 2 /2 = 56 м 2
Теперь найдем площадь многоугольника PKHSF из формулы:
SPKHSF = SPBCDF / cos 60° = 56 / 1 / 2 = 112 м 2
Рис.9 Задача. В правильной четырехугольной призме.
Пример 4
Боковая поверхность правильной четырехугольной призмы 12 м 2 . А полная поверхность 20 м 2 . Найдите высоту призмы.
Решение:
Пусть дана правильная четырехугольная призма АВСDA’B’C’D’ (Рис. 10). Так как призма имеет четыре боковые грани, то площадь одной боковой грани составляет 1/4 часть боковой поверхности.
SAA’D’D = Sбок / 4 = 12 / 4 = 3 м 2
Площадь основания призмы равна половине разности площадей между полной поверхностью призмы и ее боковой поверхностью.
2 SABCD = Sпол – Sбок = 20 – 12 = 8 м 2
Так как площадь боковой грани составляет 3 м 2 , то высоту призмы, т.е. AA’, можно найти из формулы:
Следовательно, высота призмы составляет 3 / 2 м.
Рис.10 Задача. Боковая поверхность правильной четырехугольной призмы.
Пример 5
Основание пирамиды – ромб с диагоналями 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и равна 7 м. Найдите боковую поверхность пирамиды.
Решение:
Пусть дана пирамида АВСDS (Рис. 11). Основание пирамиды – ромб ABCD с диагоналями АС = 8 м, BD = 6 м. Высота SO = 7 м.
По теореме Пифагора найдем боковые ребра SA и SD:
SA 2 = AO 2 + SO 2 = 4 2 + 7 2 = 65
SD 2 = OD 2 + SO 2 = 3 2 + 7 2 = 58
SA = , SD =
Теперь найдем сторону ромба AD:
AD 2 = AO 2 + OD 2 = 3 2 + 4 2 = 25 , AD = 5 м
Теперь по теореме косинусов найдем косинус угла α между боковыми ребрами:
AD 2 = SA 2 + SD 2 – 2 SA SD cos α = 65 + 58 – 2 cos α = 25
Отсюда, cos α = 49 / , sin α = 1369 /
Теперь найдем площадь боковой грани SASD:
SASD = SA SD sin α / 2 = 1369 / / 2 = 18.5 м 2
Отсюда, Sбок = 4 SASD = 4 * 18.5 = 74 м 2
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/pryamougolnyj-parallelepiped
http://www.mathtask.ru/0064-stereometry.php
[/spoiler]
|
||||
| 1 2 3 4 5 6 7 8 | ||||
|
Рис. 1 Двугранный угол. Трехгранный углыПусть заданы три луча a, b, c не лежащие в одной плоскости и исходящие из одной общей точки О. (Рис.1.1). Тогда трехгранным углом называется фигура, которая состоит из трех плоских углов. Точка О, из которой исходят лучи, называется вершиной трехгранного угла. Сами углы называются гранями, а стороны – ребрами. Понятие многогранного угла можно определить аналогичным образом. |
Рис. 1.1 Трехгранный угол. 2.Призма и построение ее сеченийПрямая призмаПризмой называется многогранник, у которого две стороны являются плоскими многоугольниками, лежащими в параллельных плоскостях и совмещаемых параллельным переносом, а боковые грани состоят из всех отрезков, соединяющих соответствующие точки этих многоугольников (Рис.2). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие точки оснований, ее ребрами. Высотой призмы называется расстояние между ее основаниями. Если боковые ребра призмы перпендикулярны основанию, то такая призма называется прямой. В противном случае призма называется наклонной. Боковые ребра у призмы параллельны и равны. Боковые грани прямой призмы являются прямоугольниками. Если в основании призмы лежит правильный многоугольник, то такая призма называется правильной. Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на ее высоту. В основании призмы лежит правильный многоугольник. Боковые ребра призмы находятся под прямым углом к основанию и являются высотами. Боковые грани представляют собой прямоугольники. Отсюда следует, что площадь боковой поверхности призмы равна: где Полная площадь призмы равна сумме площадей двух оснований и боковой поверхности. Рис.2 Прямая призма Наклонная призмаЕсли боковые ребра призмы находятся под некоторым углом к основанию, то призма является наклонной (Рис.2.1). Используя правила параллельного проектирования, изображение призмы можно построить следующим образом. Сначала строится одно из оснований, т.е. многоугольник, а затем проводят боковые ребра из каждой вершины основания, которые параллельны и равны между собой. Затем концы этих отрезков соединяются и строится другое основание призмы. Для того, чтобы построить сечение призмы плоскостью, сначала задают прямую g в плоскости одного из оснований, которая называется следом. Затем проводят через заданную точку В прямую, которая находится в плоскости грани, и соединяют ее с заданным следом в точке Е. Отрезок АС на рассматриваемой грани есть пересечение этой грани с секущей плоскостью. Если грань, которая содержит точку В, параллельна следу, то секущая плоскость пересекает эту грань по отрезку, параллельному заданному следу и проходящему через точку В. Таким образом, можно провести отрезки на всех гранях призмы и получить сечение плоскостью с заданным следом. Рис.2.1 Наклонная призма 3. ПараллелепипедПризма, у которой основание есть параллелограмм, называется параллелепипедом. Параллелепипед, у которого грани расположены под некоторым углом ≠ 90° к основанию, называется наклонным. В противном случае – прямым, т.е. угол между боковыми гранями и основанием = 90°. Теорема. Противолежащие грани параллелепипеда параллельны и равны. Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.3). Рассмотрим грани параллелепипеда AA’D’D и BB’C’C. Так как основания параллелепипеда параллелограммы, то сторона AD параллельна и равна стороне ВС, а сторона A’D’ параллельна и равна стороне B’C’. Сторона AB параллельна и равна стороне DС, а сторона A’B’ параллельна и равна стороне D’C’. Отсюда можно сделать вывод, что грани AA’D’D и BB’C’C лежат в параллельных плоскостях. Таким образом, грань AA’D’D совмещается параллельным переносом с гранью BB’C’C. Следовательно эти грани равны. Аналогично можно доказать параллельность и равенство граней DD’C’C и AA’B’B. Центральная симметрия параллелепипедаТеорема. Диагонали параллелепипеда пересекаются в одной точке, которая делит их пополам. Рассмотрим две грани параллелепипеда ABCD и BB’C’C. Сторона BC у них общая. Следовательно стороны AD и B’C’ равны, лежат на параллельных прямых и в одной плоскости. Так как грани параллелепипеда AA’B’B и DD’C’C лежат в параллельных плоскостях и совмещаются параллельным переносом, то диагонали AB’ и DC’ параллельны и лежат в плоскости сторон AD и B’C’. Отсюда можно сделать вывод, что AB’C’D – параллелограмм. Диагонали этого параллелограмма пересекаются в точке, которая делит их пополам. Отсюда следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии. Рис. 3 Наклонный параллелепипед. 4.Прямоугольный параллелепипедПрямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным. Длины не параллельных ребер параллелепипеда называются его линейными размерами. Теорема. В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех его измерений. Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.4). Рассмотрим прямоугольный треугольник ACC’. Cторонами данного треугольника являются диагональ параллелепипеда AC’, диагональ основания AC и ребро боковой грани CC’. Тогда по теореме Пифагора находим: Рис. 4 Прямоугольный параллелепипед. AC’ 2 = AC 2 + CC’ 2 AC 2 = AD 2 + DC 2 Следовательно: AC’ 2 = AD 2 + DC 2 + CC’ 2 Стороны AD, DC, CC’ являются линейными размерами параллелепипеда. Симметрия прямоугольного параллелепипедаПрямоугольный параллелепипед имеет центр симметрии. Если все три измерения параллелепипеда разные, то он имеет три плоскости симметрии, которые проходят через центры граний (Рис.4.1) Если параллелепипед имеет два равных измерения, то у него есть еще две плоскости симметрии, которые проходят через диагональные сечения. Если у параллелепипеда все три линейные размера равны, то он является кубом. И у него девять плоскостей симметрии. Рис. 4.1 Симметрия прямоугольного параллелепипеда. 5. Пирамида Пирамидой называется многогранник, который состоит из многоугольника в основании, точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершины многоугольника и данную точку (Рис.5). Точка, не лежащая в плоскости основания, называется вершиной пирамиды. Отрезки, соединяющие вершины основания с вершиной пирамиды, называются боковыми ребрами. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется высотой пирамиды. На рисунке 5 изображена пирамида, в основании которой лежит правильный шестиугольник. A1A2A3A4A5A6 Построение пирамиды и ее плоских сеченийДля того чтобы построить пирамиду, необходимо сначала построить основание – плоский многоугольник. Затем взять точку, не лежащую в плоскости основания, и соединить ее боковыми ребрами с вершинами основания. Сечения пирамиды, проходящие через ее вершину, представляют собой треугольники. Например, треугольниками являются диагональные сечения, т.е. сечения, проходящие через два несоседних боковых ребра . Сечение пирамиды с боковым следом строится аналогично, как и сечение призмы (Рис.5). Т.е. сначала задается прямая в плоскости основания – след g. Затем берется какая-нибудь точка В, принадлежащая сечению, и строится пересечение следа g секущей плоскости c плоскостью этой грани – точка D. Полученный таким образом отрезок АС, представляет собой линию пересечения плоскости грани и плоскости сечения пирамиды. Если точка В лежит на грани, параллельной следу g (Рис.5.1), то секущая плоскость пересекает эту грань по отрезку BC, параллельному следу g. Концы отрезка также соединяют со следом по прямой ED в плоскости α другой грани и получают прямую пересечения этой грани с плоскостью сечения и т.д. Таким образом можно построить линии пересечения плоскости сечения со всеми гранями пирамиды. Рис. 5.1 Построение пирамиды и ее плоских сечений. 6. Усеченная пирамидаТеорема. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду. Пусть дана пирамида ABCDES. ABCDE – основание пирамиды, пятиугольник. S – вершина пирамиды. α – секущая плоскость. Подвергнем пирамиду преобразованию подобия (гомотетии) с коэффициентом подобия k относительно вершины S. Так как при преобразовании подобия расстояние от вершины до точек фигуры изменяется в одно и тоже k число раз, то пятиугольник в основании переходит в плоскость α, параллельную основанию, т.е. секущую плоскость. Точки A’B’C’D’E’ – точки пересечения боковых ребер пирамиды с плоскостью α. И пирамида, которая образуется путем отсечения данной пирамиды плоскостью α, является подобной данной. Правильная пирамидаЕсли основание пирамиды есть правильный многоугольник, а основание высоты совпадает с центром этого многоугольника, то такая пирамида называется правильной. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему. Рис. 6 Усеченная пирамида. |
|||
|
Рис. 6 Правильные многогранники. |
||||
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение угла между прямыми
(blacktriangleright) Угол между прямыми – это такой угол (alpha), что (0leqslant alphaleqslant 90^circ).
(blacktriangleright) В пространстве существует 4 типа взаимного расположения прямых: совпадают, пересекаются, параллельны, скрещиваются.
(blacktriangleright) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
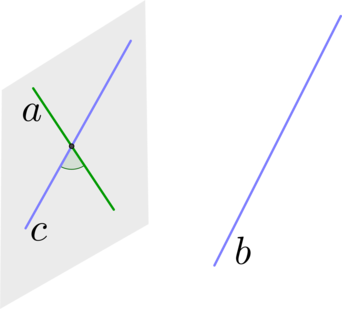
(blacktriangleright) Порядок нахождения угла между скрещивающимися прямыми:
Шаг 1: через одну из двух прямых (a) провести плоскость, параллельную второй прямой (b) (напомним признак: прямая параллельна плоскости, если она параллельна какой-нибудь прямой из этой плоскости);
Шаг 2: в этой плоскости найти прямую (c), параллельную прямой (b);
Шаг 3: тогда угол между прямыми (a) и (b) будет равен углу между прямыми (a) и (c).
Задание
1
#934
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.
Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).
Ответ: 90
Задание
2
#2847
Уровень задания: Равен ЕГЭ
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.
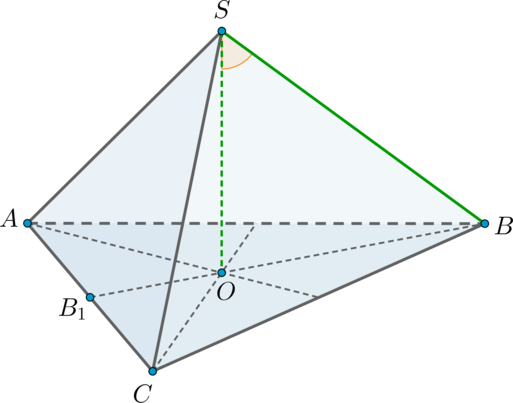
Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).
Ответ: 45
Задание
3
#933
Уровень задания: Равен ЕГЭ
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.
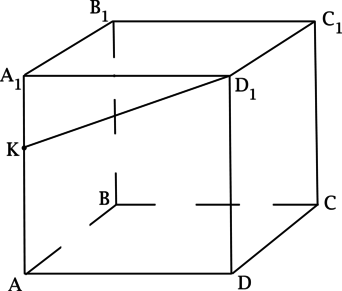
Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).
Ответ: 90
Задание
4
#2845
Уровень задания: Равен ЕГЭ
Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).
Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.
Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).
Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]
Ответ: 8
Задание
5
#1846
Уровень задания: Равен ЕГЭ
Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.
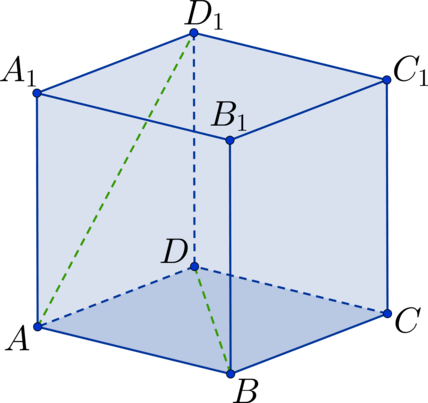
Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).
Ответ: 60
Задание
6
#1847
Уровень задания: Равен ЕГЭ
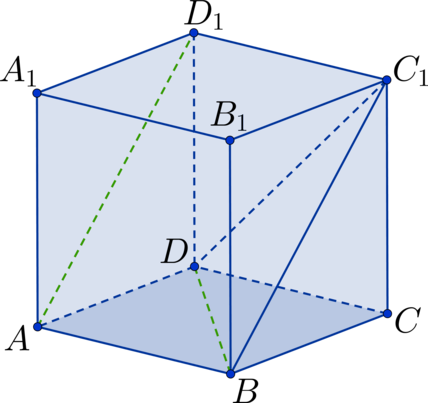
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.
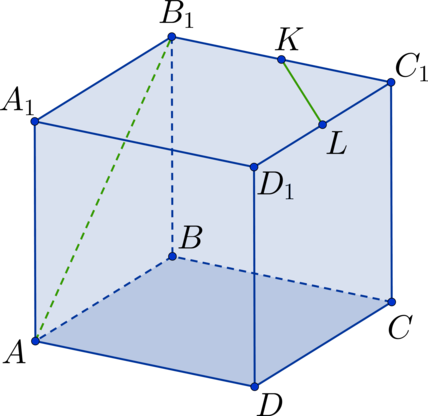
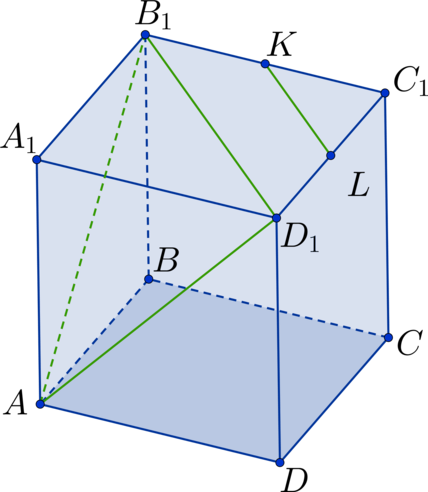
Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).
Ответ: 60
Задание
7
#2846
Уровень задания: Сложнее ЕГЭ
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).
Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.
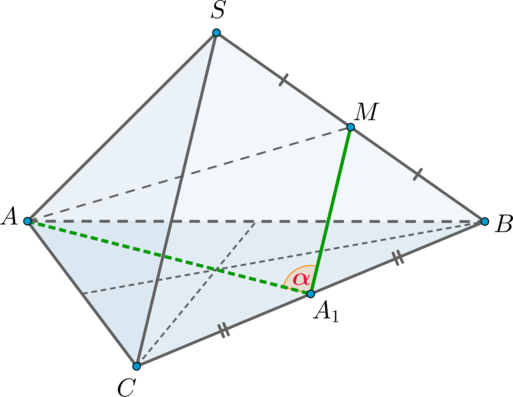
Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]
Ответ: 0,25
Каждому школьнику, который готовится к ЕГЭ по математике, будет полезно повторить тему «Нахождение угла между прямыми». Как показывает статистика, при сдаче аттестационного испытания задачи по данному разделу стереометрии вызывают трудности у большого количества учащихся. При этом задания, требующие найти угол между прямыми, встречаются в ЕГЭ как базового, так и профильного уровня. Это значит, что уметь их решать должны все.
Основные моменты
В пространстве существует 4 типа взаимного расположения прямых. Они могут совпадать, пересекаться, быть параллельными или скрещивающимися. Угол между ними может быть острым или прямым.
Для нахождения угла между прямыми в ЕГЭ или, например, в решении задач по теореме о трех перпендикулярах, школьники Москвы и других городов могут использовать несколько способов решения задач по данному разделу стереометрии. Выполнить задание можно путем классических построений. Для этого стоит выучить основные аксиомы и теоремы стереометрии. Школьнику нужно уметь логически выстраивать рассуждение и создавать чертежи, для того чтобы привести задание к планиметрической задаче.
Также можно использовать векторно-координатный метод, применяя простые формулы, правила и алгоритмы. Главное в этом случае — правильно выполнить все вычисления. Отточить свои навыки решения задач по стереометрии и другим разделам школьного курса вам поможет образовательный проект «Школково».
УСТАЛ? Просто отдохни
Перед вами очередная статья с параллелепипедами. Представленные задания просты, вычислений никаких нет или их минимум. Рассматриваются кубы и прямоугольные параллелепипеды. Важно грамотно выполнить построения и знать элементарные свойства. Например, в данных заданиях используются:
1. В равностороннем треугольнике все его углы равны 60 градусам.
2. Диагонали граней куба равны.
3. Диагонали прямоугольника равны и точкой пересечения делятся пополам.
4. Необходимо понимание понятия — скрещивающиеся прямые.
Напомню какая призма является правильной.
Правильная призма – это призма основания которой – правильные многоугольники, боковые рёбра расположены под прямым углом к основаниям. Например, правильная треугольная призма – это прямая призма, основания которой равносторонние треугольники.
Правильная четырёхугольная призма – это прямая призма, основания которой являются квадратами. Понятно, что такая призма является прямоугольным параллелепипедом.
Правильная шестиугольная призма – это прямая призма, основания которой являются правильными шестиугольниками. Рассмотрим задачи:
315130. В кубе ABCDA1B1C1D1 точка К — середина ребра АA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.
Построим куб, обозначим его вершины и точки K, M и L.
Так как данные точки являются серединами ребёр, то отрезки KM, ML, KL будут равны между собой. Это означает, что треугольник KML равносторонний. Известно, что в равностороннем треугольнике его углы равны по 60 градусов. Таким образом, угол MLK равен 600.
Ответ: 60
316554. В кубе ABCDA1B1C1D1 найдите угол между прямыми АD1 и B1D1. Ответ дайте в градусах.
Построим куб, обозначим вершины и данные отрезки, также построим отрезок АВ1.
Отрезки АD1, B1D1 и АD1 являются диагоналями граней куба, то есть все они равны, значит треугольник АD1B1 является равносторонним. Известно, что в равностороннем треугольнике его углы равны по 60 градусов.
Таким образом, угол между прямыми АD1 и B1D1 равен 600.
Ответ: 60
318474. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер AB = 8, AD = 6, AA1 = 21. Найдите синус угла между прямыми CD и A1C1.
Построим отрезки CD и A1C1:
В данной задаче имеем скрещивающиеся прямые, то есть сами они не имеют общей точки пересечения. Но этот угол между скрещивающимся прямыми определяется. Как?
Простыми словами: если вы мысленно представите в пространстве две непараллельные прямые, то всегда существует такой перпендикуляр, который их соединяет. Так вот, если мы параллельным переносом сдвинем одну прямую к другой по этому перпендикуляру до пересечения этих прямых, то полученный между ними угол и будет тем самым искомым углом.
В кубах и параллелепипедах, где прямые проходят через рёбра и диагонали такие углы определить несложно. А вот в части С присутствуют задания со скрещивающимися прямыми на порядок сложнее.
Вернёмся к нашей задаче.
Мысленно сдвинем отрезок CD вдоль перпендикуляра СC1 до пересечения с прямой A1C1. Получается, что необходимо найти синус угла между A1C1 и C1D1. Это мы можем сделать воспользовавшись определением синуса в прямоугольном треугольнике А1C1D1. Найдём:
По определению синуса:
Ответ: 0,6
318475. В правильной четырёхугольной призме ABCDA1B1C1D1 известно, что AC1 = 2BC. Найдите острый угол между диагоналями BD1 и CA1. Ответ дайте в градусах.
Построим правильную четырёхугольную призму, обозначим вершины, построим диагонали BD1 и CA1:
Сразу отметим, что диагонали BD1 и CA1 являются диагоналями прямоугольника A1BCD1, то есть они равны между собой и равны диагонали AC1 (так как призма правильная четырехугольная).
Известно, что диагонали прямоугольника равны и точкой пересечения делятся пополам, то есть:
A1С = D1B
A1O = ОС и D1O = ОB
A1O = ОС = D1O = ОB
В условии сказано, что AC1 = 2BC, значит имеем BD1 = CA1 = 2BC. На основании изложенного можем сделать вывод о том, что:
BO = ОС = BC и A1O = ОD1 = A1D1
то есть треугольники BОС и A1OD1 равносторонние.
Таким образом, угол острый между диагоналями равен 600.
Ответ: 60
В данных заданиях используется теорема Пифагора, для нахождения углов необходимо владеть понятиями синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике.
245359. Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Посмотреть решение
245360. Найдите расстояние между вершинами A и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3.
Посмотреть решение
245361. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.
Посмотреть решение
245362. Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.
Посмотреть решение
245363. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.
Посмотреть решение
284357. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BD1 = 3, CD = 2, AD = 2. Найдите длину ребра AA1.
Посмотреть решение
284363. В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что DD1 = 1, CD = 2, AD = 2. Найдите длину диагонали CA1.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
