Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите угол между скрещивающимися рёбрами правильного тетраэдра.
2
Чему равен угол между скрещивающимися медианами правильного тетраэдра?
Аналоги к заданию № 428: 429 Все
3
Найти угол между медианой одной из боковых граней правильного тетраэдра и скрещивающимся с ней ребром пирамиды.
4
В правильном тетраэдре ABCD найдите угол между прямыми BM и NK, где M, N, K — середины рёбер AD, BC и CD соответственно.
Аналоги к заданию № 430: 431 Все
5
Боковое ребро правильной треугольной пирамиды SABC равно 6, а косинус угла ASB при вершине боковой грани равен Точка M — середина ребра SC. Найдите косинус угла между прямыми BM и SA.
Пройти тестирование по этим заданиям
Среди огромного количества стереометрических
задач в учебниках геометрии, в различных
сборниках задач, пособиях по подготовке в ВУЗы
крайне редко встречаются задачи на нахождение
расстояния между скрещивающимися прямыми.
Возможно, это обусловлено как узостью их
практического применения (относительно школьной
программы, в отличие от “выигрышных” задач на
вычисление площадей и объемов), так и сложностью
данной темы.
Практика проведения ЕГЭ показывает, что многие
учащиеся вообще не приступают к выполнению
заданий по геометрии, входящих в экзаменационную
работу. Для обеспечения успешного выполнения
геометрических заданий повышенного уровня
сложности необходимо развивать гибкость
мышления, способность анализировать
предполагаемую конфигурацию и вычленять в ней
части, рассмотрение которых позволяет найти путь
решения задачи.
Школьный курс предполагает изучение четырех
способов решения задач на нахождение расстояния
между скрещивающимися прямыми. Выбор способа
обусловлен, в первую очередь, особенностями
конкретной задачи, предоставленными ею
возможностями для выбора, и, во вторую очередь,
способностями и особенностями
“пространственного мышления” конкретного
учащегося. Каждый из этих способов позволяет
решить самую главную часть задачи – построение
отрезка, перпендикулярного обеим скрещивающимся
прямым (для вычислительной же части задач
деление на способы не требуется).
Основные способы решения задач на нахождение
расстояния между скрещивающимися прямыми
Нахождение длины общего перпендикуляра двух
скрещивающихся прямых, т.е. отрезка с концами на
этих прямых и перпендикулярного каждой из этих
прямых.
Нахождение расстояния от одной из
скрещивающихся прямых до параллельной ей
плоскости, проходящей через другую прямую.
Нахождение расстояния между двумя
параллельными плоскостями, проходящими через
заданные скрещивающиеся прямые.
Нахождение расстояния от точки, являющейся
проекцией одной из скрещивающихся прямых, на
перпендикулярную ей плоскость (так называемый
“экран”) до проекции другой прямой на ту же
самую плоскость.
Проведем демонстрацию всех четырех способов на
следующей простейшей задаче: “В кубе с
ребром а найти расстояние между любым ребром
и диагональю не пересекающей его грани”. Ответ: ![]() .
.
1 способ.
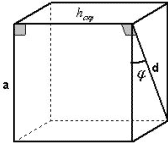
Рисунок 1
hскр перпендикулярна плоскости боковой
грани, содержащей диагональ d и
перпендикулярна ребру, следовательно, hскр
и является расстоянием между ребром а и
диагональю d.
2 способ.
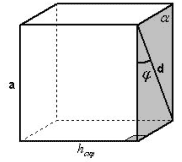
Рисунок 2
Плоскость A параллельна ребру и проходит через
данную диагональ, следовательно, данная hскр
является не только расстоянием от ребра до
плоскости A, но и расстоянием от ребра до данной
диагонали.
3 способ.
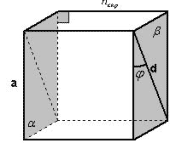
Рисунок 3
Плоскости A и B параллельны и проходят через две
данные скрещивающиеся прямые, следовательно,
расстояние между этими плоскостями равно
расстоянию между двумя скрещивающимися прямыми.
4 способ.
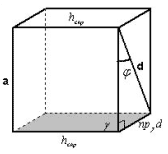
Рисунок 4
Плоскость A перпендикулярна ребру куба. При
проекции на A диагонали d данная диагональ
обращается в одну из сторон основания куба.
Данная hскр является расстоянием между
прямой, содержащей ребро, и проекцией диагонали
на плоскость C, а значит и между прямой,
содержащей ребро, и диагональю.
Остановимся подробнее на применении каждого
способа для изучаемых в школе многогранников.
СПОСОБ I.
Применение первого способа достаточно
ограничено: он хорошо применяется лишь в
некоторых задачах, так как достаточно сложно
определить и обосновать в простейших задачах
точное, а в сложных – ориентировочное
местоположение общего перпендикуляра двух
скрещивающихся прямых. Кроме того, при
нахождении длины этого перпендикуляра в сложных
задачах можно столкнуться с непреодолимыми
трудностями.
Примеры
Задача 1. В прямоугольном параллелепипеде с
размерами a, b, h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю основания.
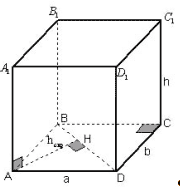
Рисунок 5
Пусть AH![]() BD.
BD.
Так как А1А перпендикулярна плоскости АВСD ,
то А1А ![]()
AH.
AH перпендикулярна обеим из двух скрещивающихся
прямых, следовательно AH?- расстояние между
прямыми А1А и BD. В прямоугольном
треугольнике ABD, зная длины катетов AB и AD, находим
высоту AH, используя формулы для вычисления
площади прямоугольного треугольника. Ответ: ![]()
Задача 2. В правильной 4-угольной пирамиде с
боковым ребром L и стороной основания a
найти расстояние между апофемой и стороной
основания, пересекающей боковую грань,
содержащую эту апофему.
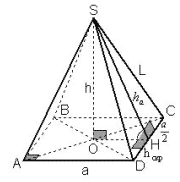
Рисунок 6
SH![]() CD как
CD как
апофема, AD![]() CD,
CD,
так как ABCD – квадрат. Следовательно, DH –
расстояние между прямыми SH и AD. DH равно половине
стороны CD. Ответ:![]()
СПОСОБ II
Применение этого способа также ограничено в
связи с тем, что если можно быстро построить (или
найти уже готовую) проходящую через одну из
скрещивающихся прямых плоскость, параллельную
другой прямой, то затем построение
перпендикуляра из любой точки второй прямой к
этой плоскости (внутри многогранника) вызывает
трудности. Однако в несложных задачах, где
построение (или отыскивание) указанного
перпендикуляра трудностей не вызывает, данный
способ является самым быстрым и легким, и поэтому
доступен.
Примеры
Задача 2. Решение уже указанной выше задачи
данным способом особых трудностей не вызывает.
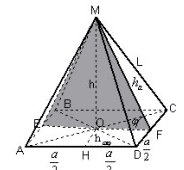
Рисунок 7
Плоскость EFM параллельна прямой AD, т. к AD || EF.
Прямая MF лежит в этой плоскости, следовательно,
расстояние между прямой AD и плоскостью EFM равно
расстоянию между прямой AD и прямой MF. Проведем OH![]() AD. OH
AD. OH![]() EF, OH
EF, OH![]() MO,
MO,
следовательно, OH![]() (EFM),
(EFM),
следовательно, OH – расстояние между прямой AD и
плоскостью EFM, а значит, и расстояние между прямой
AD и прямой MF. Находим OH из треугольника AOD.
Ответ:![]()
Задача 3. В прямоугольном параллелепипеде с
размерами a,b и h найти расстояние между
боковым ребром и не пересекающейся с ним
диагональю параллелепипеда.
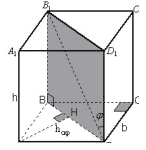
Рисунок 8
Прямая AA1 параллельна плоскости BB1D1D,
B1D принадлежит этой плоскости,
следовательно расстояние от AA1 до
плоскости BB1D1D равно расстоянию между
прямыми AA1 и B1D. Проведем AH![]() BD. Также, AH
BD. Также, AH![]() B1B,
B1B,
следовательно AH![]() (BB1D1D), следовательно AH
(BB1D1D), следовательно AH![]() B1D, т. е. AH –
B1D, т. е. AH –
искомое расстояние. Находим AH из прямоугольного
треугольника ABD.
Ответ: ![]()
Задача 4. В правильной шестиугольной призме
A:F1 c высотой h и стороной основания a
найти расстояние между прямыми:
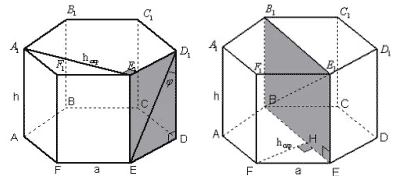
Рисунок 9 Рисунок 10
а) AA1 и ED1.
Рассмотрим плоскость E1EDD1. A1E1![]() EE1, A1E1
EE1, A1E1![]() E1D1,
E1D1,
следовательно
A1E1 ![]() (E1EDD1). Также A1E1
(E1EDD1). Также A1E1 ![]() AA1.
AA1.
Следовательно, A1E1 является
расстоянием от прямой AA1 до плоскости E1EDD1.
ED1![]() (E1EDD1).,
(E1EDD1).,
следовательно AE1 – расстояние от прямой AA1
до прямой ED1. Находим A1E1 из
треугольника F1A1E1 по теореме
косинусов. Ответ:![]()
б) AF и диагональю BE1.
Проведем из точки F прямую FH перпендикулярно BE.
EE1![]() FH, FH
FH, FH![]() BE, следовательно
BE, следовательно
FH![]() (BEE1B1),
(BEE1B1),
следовательно FH является расстоянием между
прямой AF и (BEE1B1), а значит и
расстоянием между прямой AF и диагональю BE1.
Ответ:![]()
СПОСОБ III
Применение этого способа крайне ограничено,
так как плоскость, параллельную одной из прямых
(способ II) строить легче, чем две параллельные
плоскости, однако способ III можно использовать в
призмах, если скрещивающиеся прямые принадлежат
параллельным граням, а также в тех случаях, когда
в многограннике несложно построить параллельные
сечения, содержащие заданные прямые.
Примеры
Задача 4.
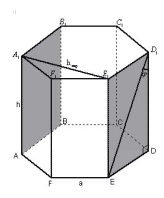
Рисунок 11
а) Плоскости BAA1B1 и DEE1D1
параллельны, так как AB || ED и AA1 || EE1. ED1![]() DEE1D1,
DEE1D1,
AA1![]() (BAA1B1),
(BAA1B1),
следовательно, расстояние между прямыми AA1
и ED1 равно расстоянию между плоскостями BAA1B1
и DEE1D1. A1E1![]() AA1, A1E1
AA1, A1E1![]() A1B1, следовательно, A1E1
A1B1, следовательно, A1E1![]() BAA1B1.
BAA1B1.
Аналогично доказываем, что A1E1![]() (DEE1D1). Т.о., A1E1
(DEE1D1). Т.о., A1E1
является расстоянием между плоскостями BAA1B1
и DEE1D1, а значит, и между прямыми AA1
и ED1. Находим A1E1 из треугольника
A1F1E1, который является
равнобедренным с углом A1F1E1,
равным ![]() .
.
Ответ:![]()
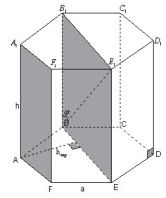
Рисунок 12
б) Расстояние между AF и диагональю BE1
находится аналогично.
Ответ:![]() .
.
Задача 5. В кубе с ребром а найти
расстояние между двумя непересекающимися
диагоналями двух смежных граней.
Данная задача рассматривается как
классическая в некоторых пособиях, но, как
правило, ее решение дается способом IV, однако
является вполне доступной для решения с помощью
способа III.
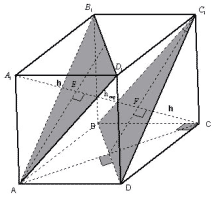
Рисунок 13
Некоторую трудность в данной задаче вызывает
доказательство перпендикулярности диагонали A1C
обеим параллельным плоскостям (AB1D1 ||
BC1D). B1C![]() BC1 и BC1
BC1 и BC1![]() A1B1, следовательно,
A1B1, следовательно,
прямая BC1 перпендикулярна плоскости A1B1C,
и следовательно, BC1![]() A1C. Также, A1C
A1C. Также, A1C![]() BD.
BD.
Следовательно, прямая A1C перпендикулярна
плоскости BC1D. Вычислительная же часть
задачи особых трудностей не вызывает, так как hскр
= EF находится как разность между диагональю куба
и высотами двух одинаковых правильных пирамид A1AB1D1
и CC1BD.
Ответ:![]()
СПОСОБ IV.
Данный способ имеет достаточно широкое
применение. Для задач средней и повышенной
трудности его можно считать основным. Нет
необходимости применять его только тогда, когда
один из трех предыдущих способов работает проще
и быстрее, так как в таких случаях способ IV может
только усложнить решение задачи, или сделать его
труднодоступным. Данный способ очень выгодно
использовать в случае перпендикулярности
скрещивающихся прямых, так как нет необходимости
построения проекции одной из прямых на “экран”
Примеры.
Задача 5. Все та же “классическая” задача
(с непересекающимися диагоналями двух смежных
граней куба) перестает казаться сложной, как
только находится “экран” – диагональное
сечение куба.
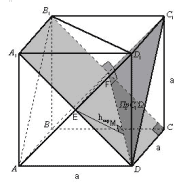
Рисунок 14
Экран:
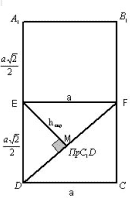
Рисунок 15
Рассмотрим плоскость A1B1CD. C1F![]() (A1B1CD),
(A1B1CD),
т. к. C1F![]() B1C
B1C
и C1F![]() A1B1.
A1B1.
Тогда проекцией C1D на “экран” будет
являться отрезок DF. Проведем EM![]() DF. Отрезок EM и будет являться расстоянием
DF. Отрезок EM и будет являться расстоянием
между двумя непересекающимися диагоналями двух
смежных граней. Находим EM из прямоугольного
треугольника EDF. Ответ:![]() .
.
Задача 6. В правильной треугольной пирамиде
найти расстояние и угол между скрещивающимися
прямыми: боковым ребром l и стороной
основания a.
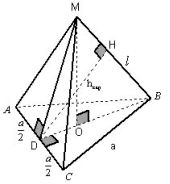
Рисунок 16
В данной и аналогичных ей задачах способ IV
быстрее других способов приводит к решению, так
как построив сечение, играющее роль “экрана”,
перпендикулярно AC (треугольник BDM), видно, что
далее нет необходимости строить проекцию другой
прямой (BM) на этот экран. DH – искомое расстояние. DH
находим из треугольника MDB, используя формулы
площади. Ответ:![]() .
.
В правильной треугольной пирамиде угол между скрещивающимися ребрами равен.
Вы находитесь на странице вопроса В правильной треугольной пирамиде угол между скрещивающимися ребрами равен? из категории Геометрия.
Уровень сложности вопроса рассчитан на учащихся 10 – 11 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.
Учебник
Геометрия, 10 класс
Угол между скрещивающимися прямыми в пространстве
Скрещивающиеся прямые – не параллельны, не имеют общих точек, не пересекаются.
Признаки Скрещивающихся прямых
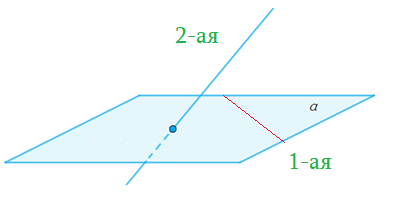
- 1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
- Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
- Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$
Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между
скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$
- Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
- Свойство инвариантности углов при параллельном переносе стереометрических объектов – прямых, плоскостей:
- Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
- В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
- Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
- Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
- *** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
- Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней – прямоугольников, значит, найти их по теоремам Пифагора.
- Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
- Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
- Признак: $NAL$ – плоскость угла: $ANin NAL$ и $BKparallel NAL$
case I 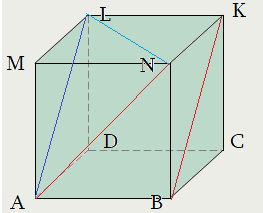 case II
case II 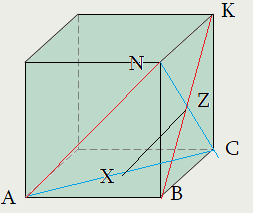
Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):
1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ – середину отрезка $BK$.
2-ой шаг: Для прямой $AN$ определим плоскость “скольжения” – плоскость, содержащая эту прямую и точку $Z$. Это $ANC$
3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно “как стержень”. Она совместится с отрезком $ZX$.
4-ый шаг: Что за точка $X$ ? угол $angle XZB$ – именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.
Признак: – увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.
Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$
- $ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
- Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
- Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ – плоскость сколжения. $AB$ перейдет в $MN$.
- Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол – это $angle CMN$.
- Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
- Признак: $CMN$ – плоскость угла: $ABparallel CMN$ и $MCin CMN$
k задачe 2 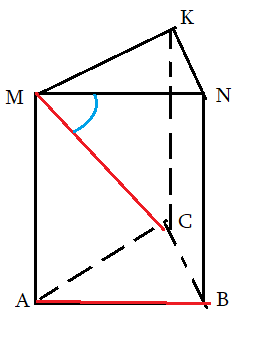 к задаче 3
к задаче 3 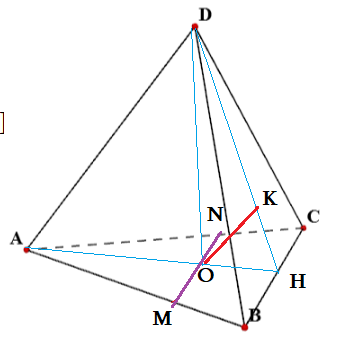
Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.
- Для нахождения угла, совместим “движениями” наши прямые в точку $O$ – основание высоты $DO$ .
- В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
- Точка $O$ – пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ – высота грани $BDC$.
- В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
- В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
- Итак, “взамен” наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
- по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
- Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
- Признак: $MONK$ – плоскость угла: $ADparallel MONK$ и $BCparallel MONK$
Алгоритм: вычисление угла в пространстве или плоскости
- В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
- Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
- А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !
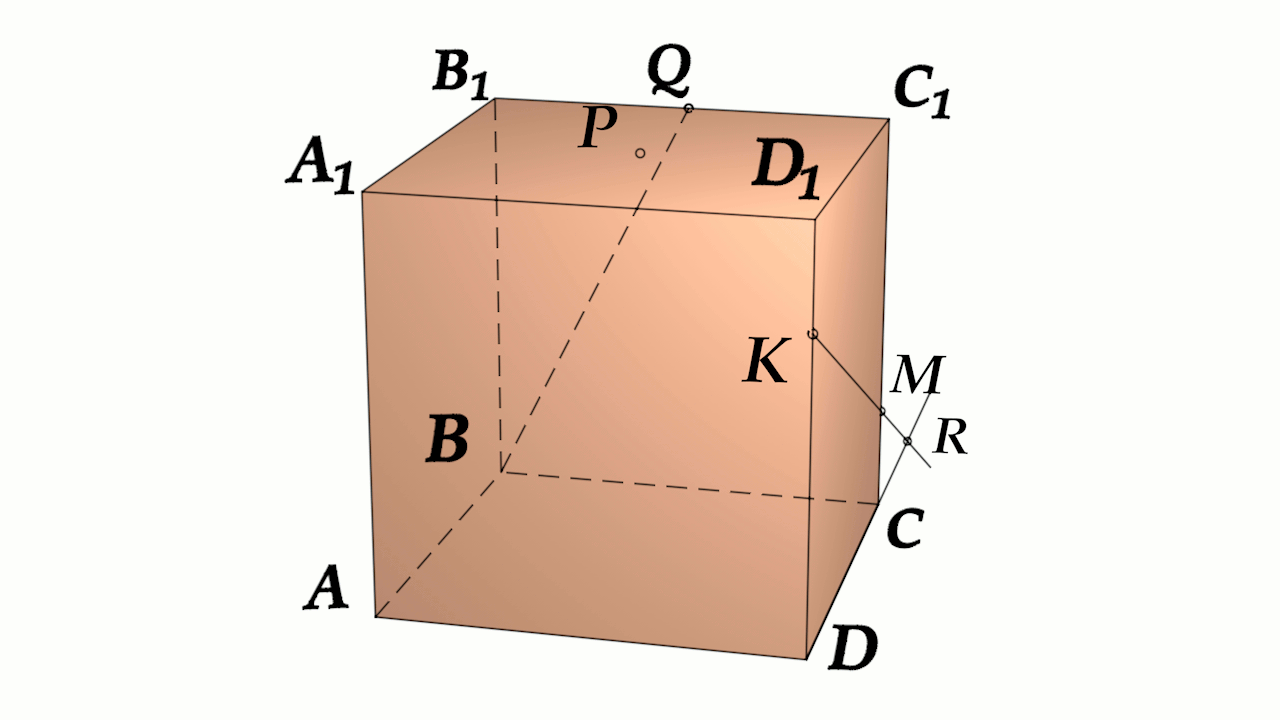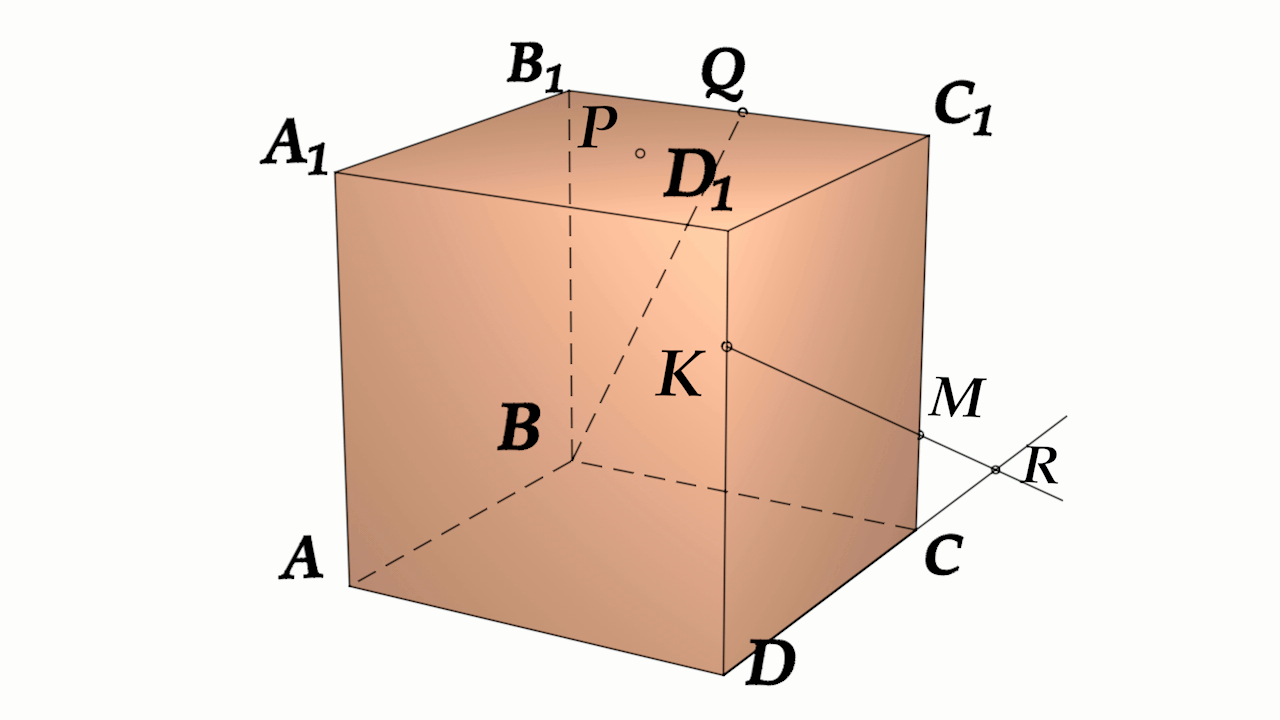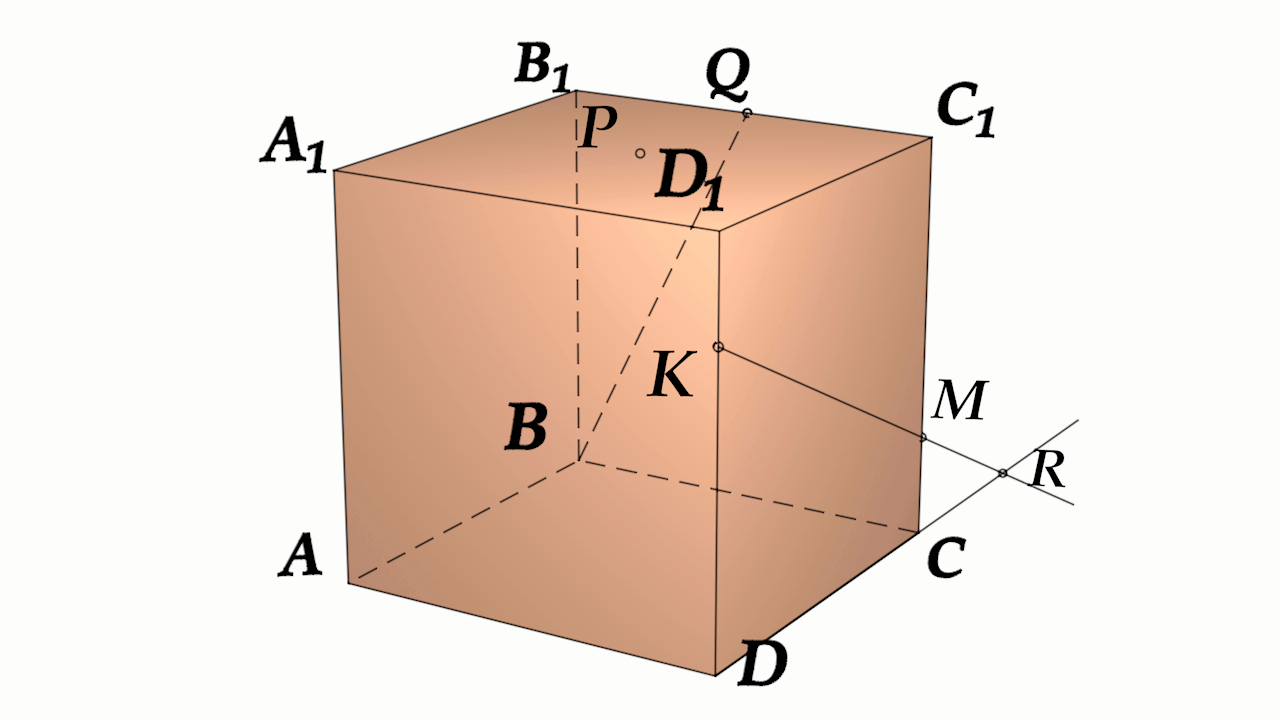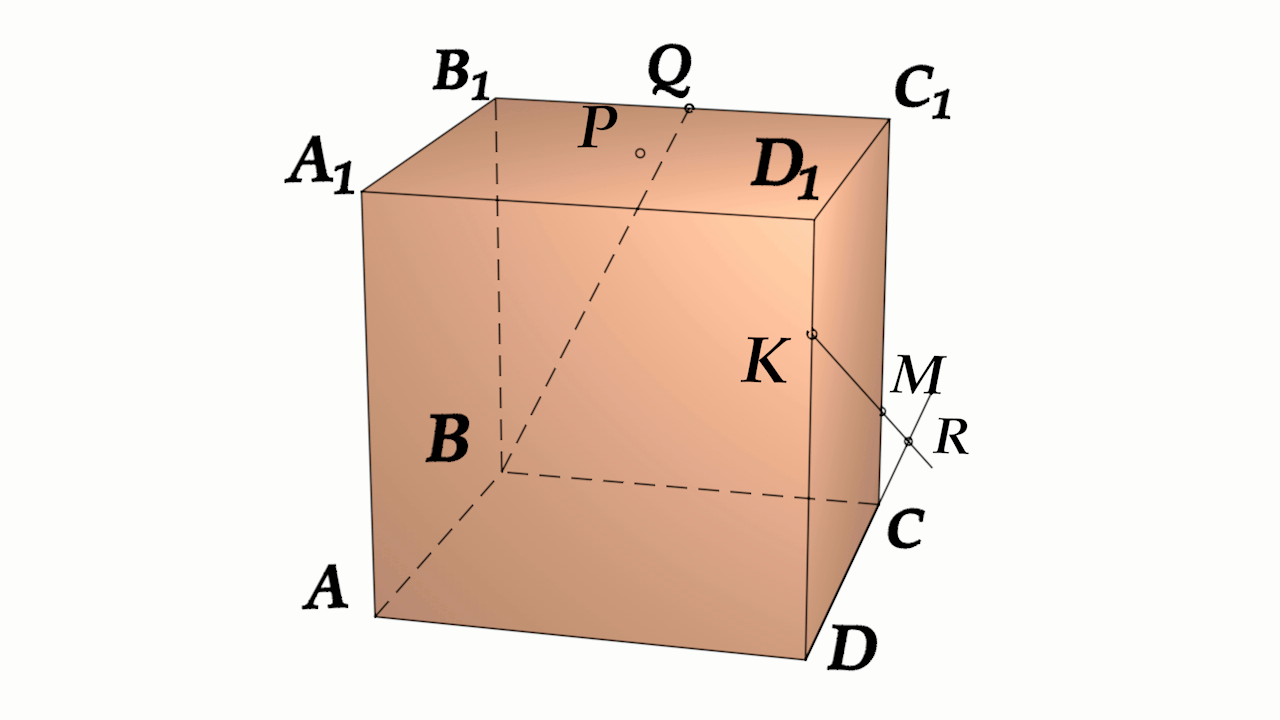
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ – середина ребра . Точка $K$
делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении
5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .

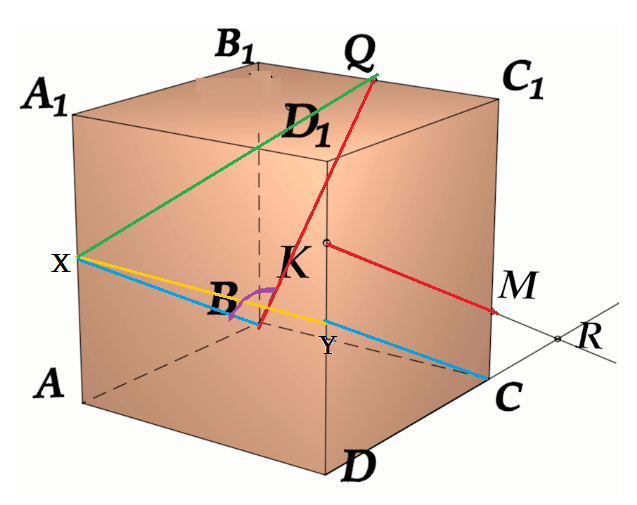
- Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
- Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
- Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
- В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
- Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
- В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
- Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
- $MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
- $BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
- Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
- Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
- Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
- наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
- Признак: $XBQ$ – плоскость угла: $KMparallel XBQ$ и $BQin XBQ$
Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит
ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.
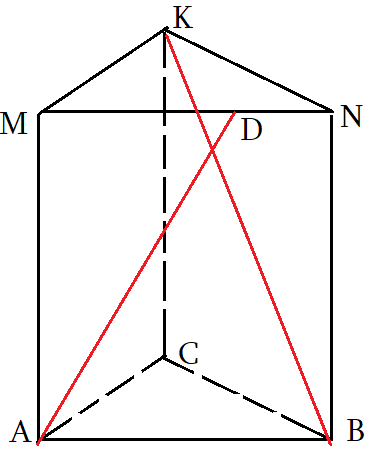
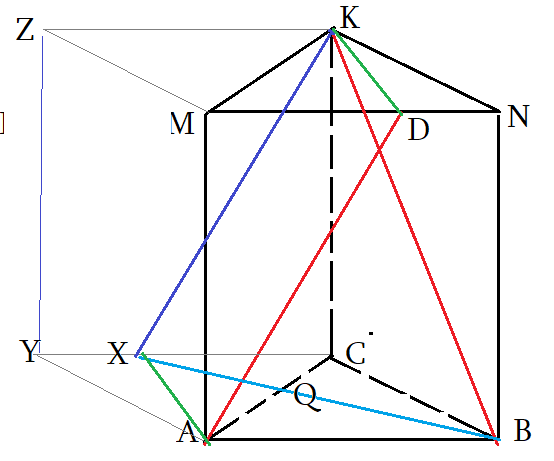
- Чтоб найти угол между скрещивающимися прямыми, нужно “подвигать параллельно” $AD$ и $BK$ до совмещения.
- Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ – т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
- Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, “движения”, плоскости будут внутри!
- $AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
- по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
- Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
- Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
- Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
- $XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
- С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
- А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
- Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ – то что надо!
- Признак: $XKB$ – плоскость угла: $ADparallel XKB$ и $BKin XKB$
Упражнения:
1. ( ABCD ) – треугольная пирамида, все грани которой являются равносторонними треугольниками с единичной стороной.
(Q)- середина стороны (AB)
(P)- середина стороны (BC . )
Найдите угол между прямыми ( DP ) и (QC)
Показать ответ
Показать решение
Видеорешение
Пусть основанием нашей пирамиды будет равносторонний треугольник (ABC)
поместим начало координат в центр вписанной окружности, а оси расположим как мы привыкли:
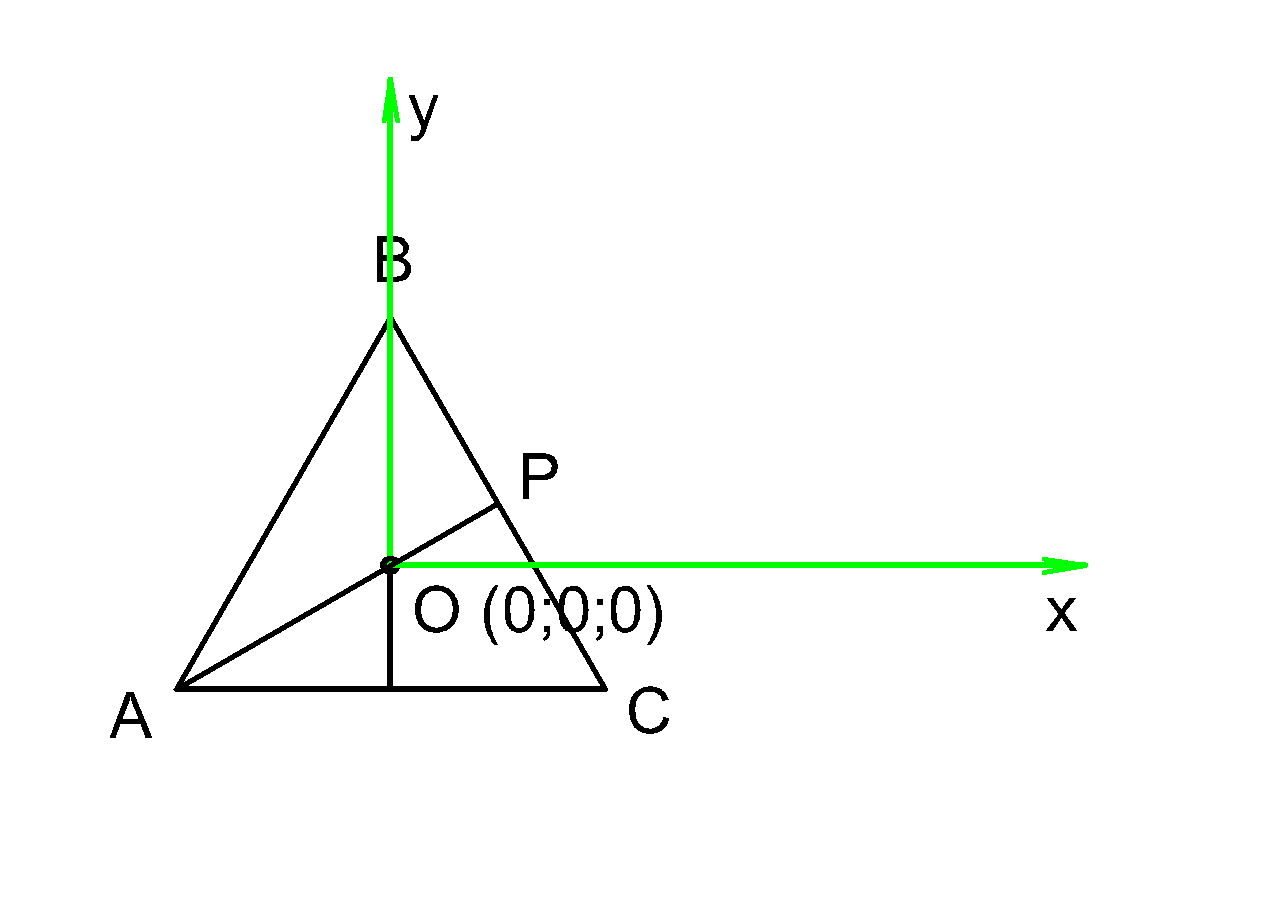
Ось ( Z ) также начинается в точке (O) и проходит через вершину (D ) нашей пирамиды, то есть направлена вертикально вверх,
поэтому на этом плоскостном рисунке мы ее не видим.
Попробуем найти координаты точки ( P: )
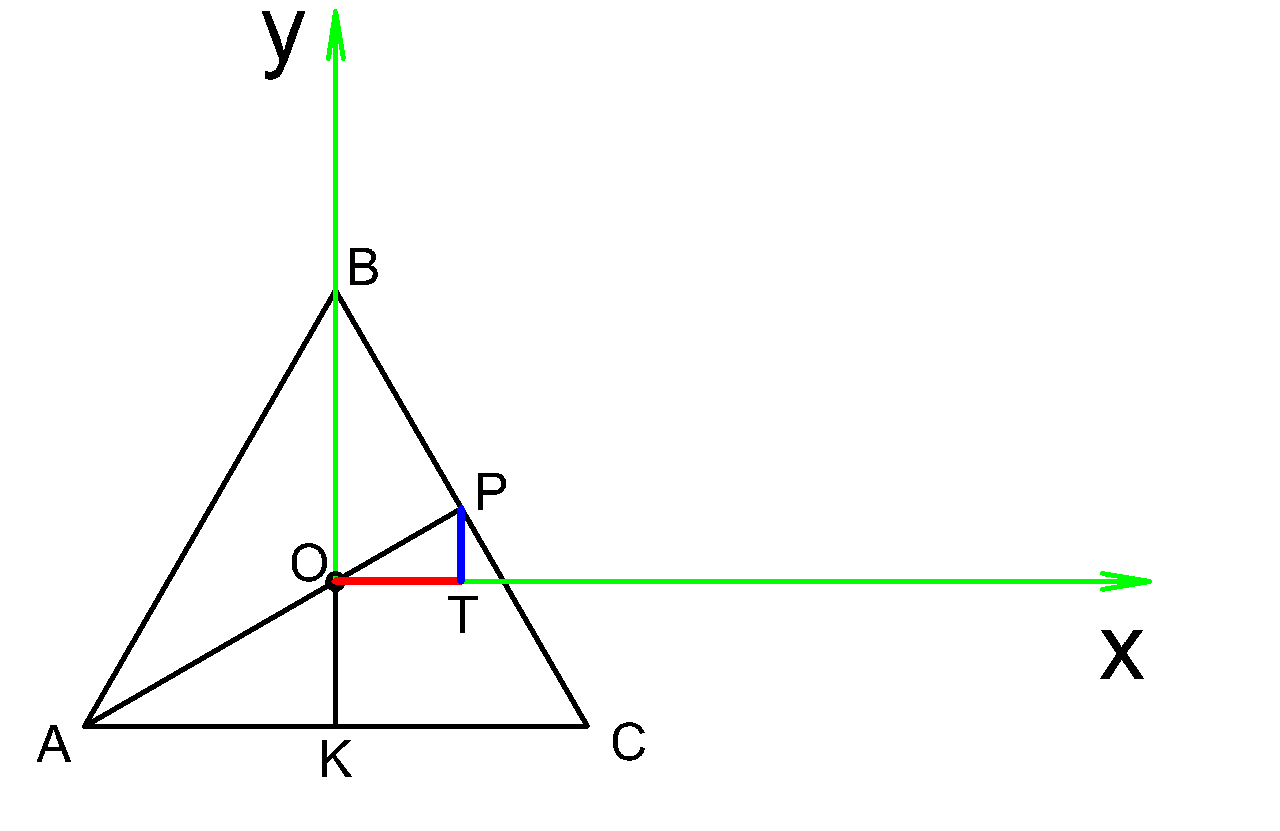
Получается длина красного отрезка ( OT ) равна абсциссе точки ( P ) ,
а длина синего отрезка (PT ) равна ординате точки ( P )
Мы знаем, что любое ребро нашей пирамиды равно единице, значит (КС= dfrac{1}{2} . )
Найдем (BK ) по теореме Пифагора:
(BK= sqrt{ 1^2- left( dfrac{1}{2} right )^2 } = dfrac{sqrt{3}}{2} )
Центр вписаной окружности делит высоту в соотношении 2:1 от вершины треугольника:
(BO=2x )
(OK=x )
(2x+x=dfrac{sqrt{3}}{2} )
(x=dfrac{sqrt{3}}{6} = OK)
(OP) в два раза меньше ( AO ) по тому же принципу.
( angle TOP=angle OAK ) (по теореме о параллельных прямых и секущей)
Поэтому треугольники ( TOP ) и ( OAK ) подобны по двум углам с коэффициентом подобия 2.
Значит (OT) в 2 раза меньше (AK)
( OT=dfrac{1}{4} )
(PT) в 2 раза меньше (OK)
(PT=dfrac{sqrt{3}}{12} )
Теперь мы знаем координаты точки ( P(dfrac{1}{4};dfrac{sqrt{3}}{12};0 ) )
Точка (Q) симметрична точке (P) относительно оси ординат, поэтому имеет такую же абсциссу, что и точка (P), но
взятую с обратным знаком.Ординаты этих точек равны.
Абсцисса точки ( C ) численно равна (KC=dfrac{1}{2}), а ее ордината длине отрезка (OK), взятая с обратным знаком.
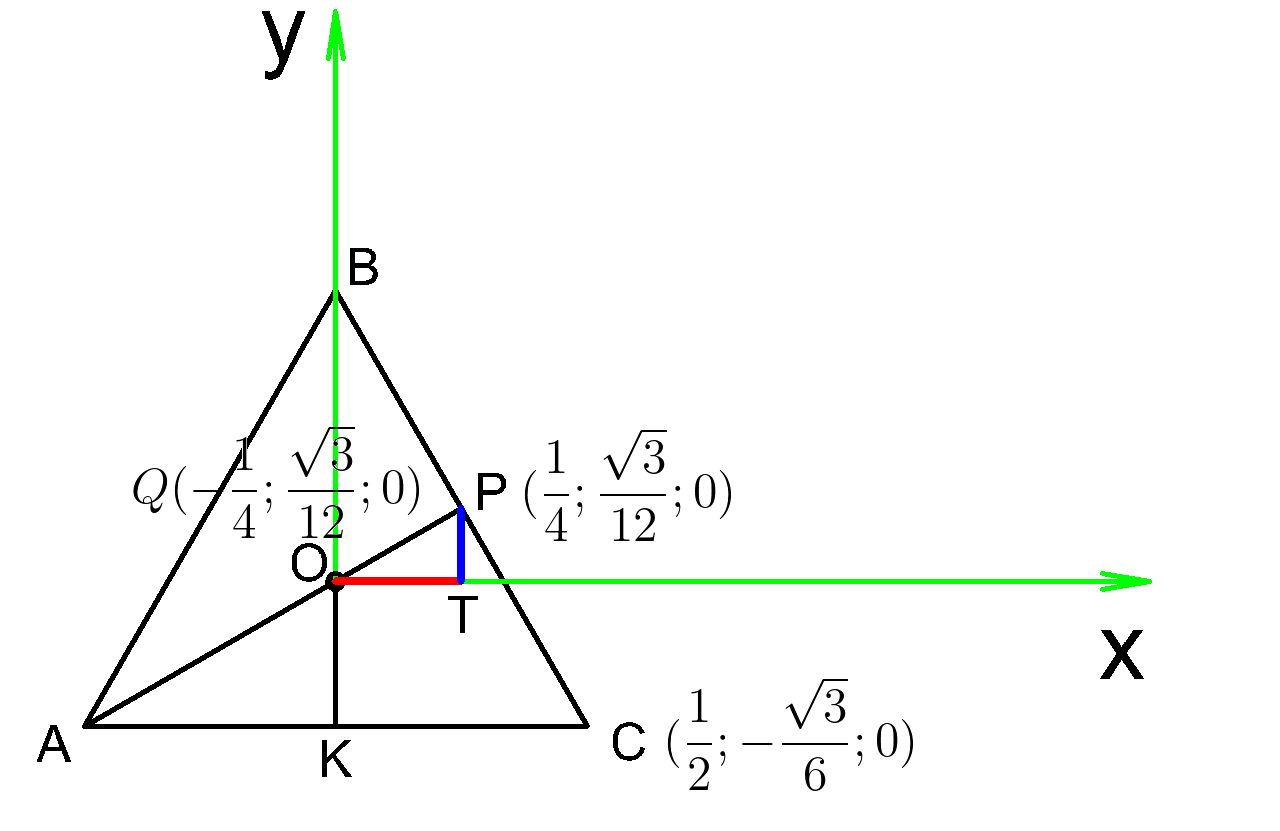
Теперь строим объемный чертеж нашей пирамиды и видим, что вершина ( D ) лежит на оси ( Z ) ,
поэтому абсцисса и ордината точки ( D ) будут равны нулю, а ( Z ) координата будет равна отрезку ( DO )
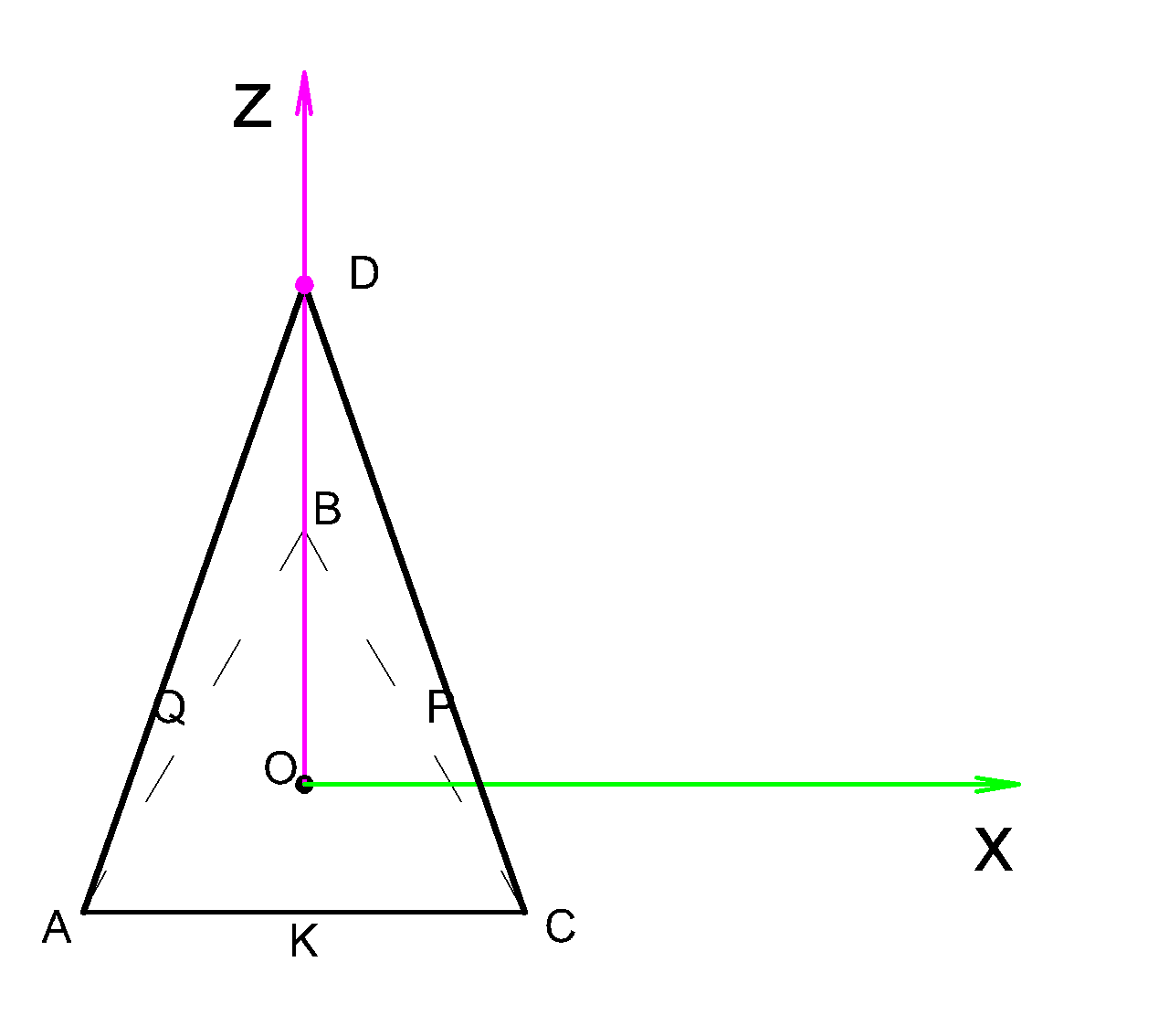
Найдем ( DO ) из треугольника ( DOK: )
(DK=BK=dfrac{sqrt{3}}{2} ) так как это высоты граней, а все грани одинаковы.
(OK =dfrac{sqrt{3}}{6} )
(DO= sqrt{ left(dfrac{sqrt{3}}{2} right )^2 – left(dfrac{sqrt{3}}{6} right )^2 } = dfrac{sqrt{2}}{sqrt{3}} )
Теперь мы знаем координаты точки ( D(0;0;dfrac{sqrt{2}}{sqrt{3}} ) )
Косинус угла между векторами ( vec{a}(x_1;y_1;z_1) и vec{b}(x_2;y_2;z_2) )
находится по формуле:
( cos alpha = dfrac{x_1 cdot x_2+y_1cdot y_2 +z_1cdot z_2 }
{ sqrt {x_{1}^2+y_{1}^2+z_{1}^2}cdot sqrt {x_{2}^2+y_{2}^2 +z_{2}^2} } )
( (x_1;y_1;z_1) ) это координаты вектора ( vec{a} )
( (x_2;y_2;z_2) ) это координаты вектора ( vec{b} )
Представим какой-то произвольный вектор ( vec{GM} )
Точка ( G {x_1;y_1;z_1 } ) это начало вектора
Точка ( M {x_2;y_2;z_2 } ) это конец вектора
Для нахождения координат вектора нужно из координат конца вектора вычесть координаты начала вектора:
(vec{GM} {x_2-x_1; y_2-y_1 ;z_2-z_1 } )
Теперь вернемся к нашим векторам (vec{QC} ) и (vec{DP} )
(vec{QC} { dfrac{1}{2}-(-dfrac{1}{4});-dfrac{sqrt{3}}{6}-dfrac{sqrt{3}}{12};0 } )
(vec{QC} { dfrac{3}{4};-dfrac{sqrt{3}}{4};0 } )
(vec{DP} { dfrac{1}{4}-0; dfrac{sqrt{3}}{12}-0;0-dfrac{sqrt{2}}{sqrt{3}} } )
(vec{DP} { dfrac{1}{4}; dfrac{sqrt{3}}{12};-dfrac{sqrt{2}}{sqrt{3}} } )
( cos alpha = dfrac{dfrac{3}{4} cdot dfrac{1}{4}+ left( -dfrac{sqrt{3}}{4} right ) cdot dfrac{sqrt{3}}{12} +0cdot
left (-dfrac{sqrt{2}}{sqrt{3}} right )}
{ sqrt {left(dfrac{3}{4}right ) ^2+left( -dfrac{sqrt{3}}{4} right )^2+0^2}cdot sqrt {left(dfrac{1}{4}right )^2+left( dfrac{sqrt{3}}{12} right )^2 +left(-dfrac{sqrt{2}}{sqrt{3}} right)^2} } )
( cos alpha = dfrac{dfrac{3}{16} -dfrac{3}{48}}
{ sqrt {dfrac{9}{16}+dfrac{3}{16}}cdot sqrt {dfrac{1}{16}+ dfrac{3}{144}+dfrac{2}{3}} } )
( cos alpha = dfrac{dfrac{1}{8}}
{ sqrt {dfrac{9}{16}+dfrac{3}{16}}cdot sqrt {dfrac{1}{16}+ dfrac{3}{144}+dfrac{2}{3}} } )
( cos alpha = dfrac{dfrac{1}{8}}
{ sqrt {dfrac{12}{16}}cdot sqrt {dfrac{108}{144}} } )
( cos alpha = dfrac{dfrac{1}{8}}
{ sqrt {dfrac{3}{4}}cdot sqrt {dfrac{3}{4}} } )
( cos alpha = dfrac{1}{8}:dfrac{3}{4}=dfrac{1}{6} )
(alpha =arccos left (dfrac{1}{6} right ) )
